Robustness of noisy quantum networks

Abstract

Quantum networks allow us to harness networked quantum technologies and to develop a quantum internet. But how robust is a quantum network when its links and nodes start failing? We show that quantum complex networks based on typical noisy quantum-repeater nodes are prone to discontinuous phase transitions with respect to the random loss of operating links and nodes, abruptly compromising the connectivity of the network, and thus significantly limiting the reach of its operation. Furthermore, we determine the critical quantum-repeater efficiency necessary to avoid this catastrophic loss of connectivity as a function of the network topology, the network size, and the distribution of entanglement in the network. From all the network topologies tested, a scale-free network topology shows the best promise for a robust large-scale quantum internet.

Introduction

Quantum networks are a paradigm of networks where the links and nodes obey the laws of quantum physics^1,2,3. Namely, the quantum links can be quantum correlations⁴, quantum couplings or dynamics^5,6, or even quantum causal relations⁷. Quantum nodes can be any system with quantum degrees of freedom. The nascent field of complex quantum networks^{4,8,9,10,11,12,13,14,15,16} is motivated both by the fundamental interest in understanding the nature and the properties of this object, as well as by the applied perspective of developing networked quantum technologies to fully harness their potential and their reach. The latter could be named for quantum-secure communications^17,18, quantum-accelerated computation^19,20,21, quantum-enhanced sensing and metrology^22,23,24, and the development of a future quantum Internet¹. However, quantum systems and states are vulnerable to noise in general. But how does this translate to the network realm, i.e., how robust are noisy quantum networks, and how is that robustness affected by the underlying graph? And how does it compare to the robustness of classical networks, which typically evolve, to non-trivial network topologies^25,26,27, such as scale-free properties, topologies that are known to maintain their functionality against random failures^28,29?

Networks are a set of nodes and links, where each link connects a pair of nodes. This naturally includes complex networks^25,30 such as the current classical Internet³¹, a snapshot of which is presented in Fig. 1a. With the goal of investigating a quantum Internet, we consider quantum networks where the links correspond to entangled pairs of qubits, each lying in a different node. Now, imagine we want to realize a quantum operation, e.g., computing, communication, or metrology, between two distant nodes of a quantum network: how can they establish entanglement between them, with a certain target fidelity F_target, given the existing quantum correlations in the quantum network?

Fig. 1: Complex quantum networks.

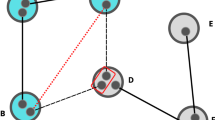
Depicted in a is a snapshot of the structure of Internet (at the level of autonomous systems using the dataset from³¹) clearly showing the scale-free properties of this complex network. This snapshot could in principle belong to a future quantum internet^{1, 48} which will, however, operate on different network principles. These differences can be seen even at the small scale. In b a small scale quantum-repeater network is shown, indicating how the connected components can intersect each other, in stark contrast to what is observed in a classical network. Here each node is represented by a black dot and the links by black lines. n_ij represents the number of entangled pairs associated with each link e_ij, which is chosen for this illustration to scale as r(l) = l. Two nodes v_i and v_j are connected at a distance l if there is a path between them such that for all links in that path satisfy the condition n_ij ≥ l, with l being the distance between node i and j. In c, d different connected components are displayed by blue green and red circle. c Illustrates a quantum network where one can only connect two nodes if n_ij ≥ l. The connected components clearly intersect each other. In contrast d illustrates a classical network where links can only be used to connect two nodes if n_ij ≥ 3. In this case the connected components do not intersect each other.

In our work, we consider an entanglement distribution network based on noisy quantum-repeater nodes, corresponding to the currently envisaged implementation of realistic long-distance quantum networks, distinctly from noiseless, pure-state, quantum networks^4,12, and from networks based on quantum channels' upper-bound capacities^{9,10,11,12,14,15,16}. Let us consider the general scenario where there are N_ij noisy Bell pairs with fidelity F_initial connecting nodes v_i and v_j. If necessary, these noisy Bell pairs can be purified to yield n_ij = N_ij/N_ft pairs exceeding a given target fidelity F_target (where N_ft is the number of initial pairs necessary to generate one F_target pair)³². Next, entanglement swapping between link v_i and v_j and link v_j and v_k consumes those Bell pairs to create a longer-range entangled pair between nodes v_i and v_k with fidelity ${F}_{{{{{{{{\rm{target}}}}}}}}}^{2}$³³. That drop in fidelity means multiple pairs need to be available for entanglement purification to return the target fidelity F_target (again consuming more pairs). These entanglement swapping and purification operations continue at longer distances until we have connected the nodes/users who want to communicate in the network³⁴. A critical question that arises is the resource consumption in such an approach. Fortunately, it is well known that resources required for the first-generation quantum-repeater network scale polynomially with the number of links l needed to connect the source node Alice and Bob³⁵. To the leading order in this polynomial, we can define³⁵,

$$R(l)={l}^{\alpha +1}=r(l)l$$

(1)

as being the number of entangled qubit pairs in the entire chain necessary to create the connected entangled qubit pair with the desired fidelity F_target, and r(l) = l^α is the number of entangled qubit pairs necessary to create the connected entangled qubit pair with the desired fidelity F_target per link. Above α represents the efficiency of the protocol which of course depends heavily on the experimental apparatus used for the repeater scheme and the noise present in it but values in the range [1, 2] are not uncommon (see Supplementary Note 1, Figs. S1 and S2 for further details).

In this work we will show that large-scale quantum networks based on noisy quantum-repeater nodes connected by noisy channels are prone to discontinuous phase transitions and that such transitions can be suppressed if the efficiency of the quantum-repeater protocol is above a certain threshold.

Results

The exploration of the connectivity of a quantum-repeater network requires the introduction of two types of connection between nodes, which we are going to call functional and structural connectivity. Functional connectivity in the quantum regime is the situation where a connection between the two nodes can be established with the required fidelity F_target. Structural connectivity on the other hand refers to the situation where a connection can be made since there is a path connecting the two nodes, but not necessary with fidelity F_target. We will illustrate these two concepts in Fig. 1b, c, d where the nodes v₁ and v₃ (and v₃ and v₅) can individually establish connections with sufficient fidelity F_target (functionally connected), but v₁ and v₅, while connected, can not (structurally connected). This means v₁ does not belong to the same “functionally” connected component as v₅ making it impossible to establish a connection between them with the required fidelity.

Standard Bernoulli percolation, a widely used technique to explore the robustness of classical networks^25,36, can not be used in these quantum scenarios due to the quality of service F_target requirement (except in the limit α = 0). Although in Bernoulli-percolation theory, finding the largest connected component of a network is a computationally easy problem to solve²⁵, finding the largest functional component of these networks is an NP-hard problem and can be related to the maximum clique-problem³⁷ (see supplementary Note 2 for details). Our model is more manageable if one considers the case where all links operate with the same amount of purification and therefore using the same number of entangled qubit pairs in each link, n^op. Let us call this quantity the operational number of entangled qubit pairs. The operational number of entangled qubit pairs is a free variable that one can tune in order to maximize network connectivity. It is also associated with an operational distance ${l}^{{{{{{{{\rm{op}}}}}}}}}={\left({n}^{{{{{{{{\rm{op}}}}}}}}}\right)}^{1/\alpha }$, meaning each link can be functionally used in paths of length l^op or less.

Our concept of a quantum functional connection naturally suggests that we should choose the operational number of entangled qubit pairs n^op as large as possible in order to increase the operational distance l^op and therefore allow for nodes further away from each other to distribute Bell pairs with our required fidelity F_target. However, increasing the operational number of entangled qubit pairs reduces the probability of a given link having the required number of entangled pairs. Thus there is an important trade-off to consider. If the number of pairs distributed between nodes can be expressed as a function g(n), then the probability that a given link has the required operational number of entangled qubit pairs or more is given by,

$${p}_{{{{{{{{\rm{op}}}}}}}}}({l}^{{{{{{{{\rm{op}}}}}}}}})=\int\nolimits_{{n}^{{{{{{{{\rm{op}}}}}}}}} = {\left({l}^{{{{{{{{\rm{op}}}}}}}}}\right)}^{\alpha }}^{+\infty }g(n)dn=\int\nolimits_{{\left({l}^{{{{{{{{\rm{op}}}}}}}}}\right)}^{\alpha }}^{+\infty }g(n)dn$$

(2)

which indicates that for n^op larger than a certain value, most links are removed from the network and there is no giant component. Instead one needs to find the smallest value of n^op, such that the operational distance is larger or equal to the diameter of the network d, (l^op ≤ d). The diameter of the network is defined as the largest distance between any two nodes in the connected component²⁵, therefore any two nodes (associated with the connected component) are able to establish a functional connection (see Fig. 2). This set of nodes is termed the backbone and serves two purposes, first, it can be used as a measure of the connectivity of the network, and second for large networks, they will behave similarly to classical communication networks. Routing developed for classical networks^38,39 should be sufficient (although not necessarily optimal) to find a good path to connect two nodes with fidelity F_target. In such a situation our method guarantees the existence of at least one path connecting any two nodes in the backbone, but given the possible existence of several paths connecting two nodes, if the backbone is large, one could also use a multi-path routing approach to generate multiple entangled qubit pairs between them, using different routes, a strategy already proposed in relation to quantum networks^9,10.

Fig. 2: Quantum network backbone.

Illustration of how the quantum backbone can be computed where the numbers written in each link represents the number of entangled pairs contained in it. We begin in a with a D = 3 network and the operational distance l^op = 0 meaning none of the links in the network need to be removed. As the operational distance l^op is increased from 1b to 2c we see that we have removed links with n_ij < 2. Further in c we notice that the distance of the network increases from D = 3 to D = 4 due to the v₅–v₆ link being removed in b due to lack of resources. Then in d, e we continue to remove various links until we reach an operational distance that is largest than the diameter of the network. We are now left in e where the largest connected network component, termed our quantum backbone. Finally in f we superimpose this quantum backbone (shown in red) onto the entire network. The size of the backbone (number of nodes in the largest connected component of the backbone) is the number of red nodes nodes in f, namely 6.

One should vary the operational distances l^op for any change in the network (like the removal of nodes and links) in order to maximize the size of the backbone. One wants to establish the repeater network with just enough resources to reach the diameter of the largest connected network component (l^op = d ideally), but the question arises how the diameter of the network d and the operational distance l^op change when now one considers that links can fail randomly with p^ext. The diameter of the network will depend on the probability that a link both has sufficient pairs to create our link (p^op) and that there has not been any random failure in that link is given p^ext. The total probability that a link is both operational and not removed is therefore p = p^opp^ext, and for a given network one can write the diameter as $\,{{\mbox{d}}}\,\left({p}^{{{{{{{{\rm{op}}}}}}}}}{p}^{{{{{{{{\rm{ext}}}}}}}}}\right)$. The operational distance on the other hand can be written solely as a function of the operational portability p^op by inverting Eq. (2). This leads us to the equation,

$${l}^{{{{{{{{\rm{op}}}}}}}}}({p}_{0}^{{{{{{{{\rm{op}}}}}}}}})=\,{{\mbox{d}}}\,\left({p}_{0}^{{{{{{{{\rm{op}}}}}}}}}{p}^{{{{{{{{\rm{ext}}}}}}}}}\right)$$

(3)

At this point ${p}_{0}^{{{{{{{{\rm{op}}}}}}}}}$ we have the minimal number of resources required to reach the diameter of the network’s largest connected component. After we find ${p}_{0}^{{{{{{{{\rm{op}}}}}}}}}$, the size of the backbone can be easily computed as the number of nodes in the largest connected component of the network composed of only links with sufficient pairs to create the link, and the link was not removed due to random failures. In the example of Fig. 2, since there are no random failures the size of the backbone is 6. Adding random failures just means that we are starting with a network with some of the links already removed. Our approach is slightly simplistic in that we have only considered links (loss of nodes can also be incorporated). We are now at the stage where we can explore actual networks.

Quantum Erdős-Rényi networks

There are of course many well-known network models we could examine with the Erdős-Rényi model network probably being the simplest^25,40. In the Erdős-Rényi model, N nodes are randomly connected to each other using L = cN/2 links, where c is the average number of links incident to each node. This model has been well explored in complex network theory^25,40 and as such, it is a good starting point, especially as one can compute l(p^op) and D(p^opp^ext) analytically⁴¹ when the number of nodes N → ∞ (asymptotic limit). Considering only bond percolation (loss of links) we show in Fig. 3 that the quantum backbone for a large Erdős-Rényi network is prone to an abrupt phase transition. We observe that the size of the quantum backbone actually drops abruptly as the probability of links not failing p^ext drops between a critical probability ${p}_{c}^{{{{{{{{\rm{ext}}}}}}}}}$. As it is usual in a first-order phase transition we observe hysteresis, therefore the critical probability ${p}_{c}^{{{{{{{{\rm{ext}}}}}}}}}$ is not well defined and the phase transition might occur in a range of probabilities between ${p}_{c1}^{{{{{{{{\rm{ext}}}}}}}}} \; < \; {p}^{{{{{{{{\rm{ext}}}}}}}}} \; < \; {p}_{c2}^{{{{{{{{\rm{ext}}}}}}}}}$, with ${p}_{{{{{{{{\rm{c1}}}}}}}}}^{{{{{{{{\rm{op}}}}}}}}},({p}_{{{{{{{{\rm{c2}}}}}}}}}^{{{{{{{{\rm{op}}}}}}}}})$ corresponding to the largest, (smallest) probability of links not failing where the phase transition might occur. This hysteresis region whose span grows with the size of the network is shown in Fig. 4 (see Supplementary Note 3 for the analytical calculations). We observe that, when the average number of entangled pairs in each link of the network is larger than a critical number of qubit pairs n_c, the traditional percolation phase transition is recovered as shown in Fig. 4 (Supplementary Note 4 for details). The critical number of qubit pairs n_c increases quickly with the size of the network (see Supplementary Note 4 for details). It is useful to mention that we have used α = 1 as a conservative value (see Supplementary Note 1). As α increases the average number of qubit pairs necessary to avoid the discontinuous phase transition will also increase.

Fig. 3: Robustness of a quantum Erdős-Rényi network.

Exploration of bond percolation on a quantum Erdős-Rényi network (ER) with average degree c = 6 where the number of entangled pairs in each link follows an exponential distribution with mean number 〈n〉. We plot the operational distance l^op and the network diameter d versus the probability that links are both operational and not removed p = p^opp^ext, for $\langle n\rangle ={\left(15\ln N\right)}^{\alpha }$ with α = 1 in a and $\langle n\rangle ={\left(15\ln N\right)}^{\alpha }$ with α = 2 in b, respectively. The large colored dots indicate their intersection. Here the operational distance l^op and network diameter d are scaled by $\ln N$ for ease of comparison. Labelled are the curves l^op(p^op) for ${p}^{{{{{{{{\rm{ext}}}}}}}}}={p}_{{{{{{{{\rm{c1}}}}}}}}}^{{{{{{{{\rm{ext}}}}}}}}}$ (${p}_{{{{{{{{\rm{c2}}}}}}}}}^{{{{{{{{\rm{ext}}}}}}}}}$) which correspond to the smallest (largest) value of p indicating a stable l^op(p^op) = D(p^opp^ext) solution in the subcritical regime. Further the classical percolation critical probability p_c gives the point where the networks breaks completely apart to become structurally disconnected meaning there is no giant set of nodes that can connect to each other with any fidelity. We generated one Erdős-Rényi network for each value of N, then d^op(p) was determined by removing each link of the network with probability 1 − p. d^op(p) was computed based on 100 runs for each value of p. The intersection between the two nodes at p₀, is marked by blue dots for solutions in the supercritcal regime, and red dots for solutions in the subcritical regime. Next the size of the backbone (number of nodes in the backbone) is plotted as a function of in b for α = 1. intersection point found in a, b) there is a corresponding size in c, d. Finally the size of the backbone is plotted as a function of the probability that links are not removed p^ext in e, f for α = 1, 2. The functionally connected regime is represented as the blue region while the functionally subcritical regime is shown as the light red region. The blue/red stripped area represents the region where both the functionally connected and subcritical regimes are stable. The dark red region on the other hand represents the structurally disconnected regime for a network of size N = 10⁵. Shaded region around each curve represents the standard deviation of the same.

Fig. 4: Phase diagram of a quantum Erdős-Rényi network.

Depicted are phase diagrams of $\langle n\rangle /\ln N$ versus the probability that a link is not removed p^ext for a quantum Erdős-Rényi network network comprised of N = 10⁴ (a), 10⁵ (b), and 10⁶ (c) nodes, respectively, with c = 6 average degree and α = 1. Here we assume the number of entangled pairs in each link follows an exponential distribution with mean 〈n〉. The functionally supercritcal regime is represented as the blue region while the functionally subcritical regime is the light red region. Further the stripped (blue/light red) area represents the region where both the functionally connected and subcritical regime are stable. The dark red region represents the structurally disconnected regime. Next the classical percolation critical probability p_c is the point where the networks breaks completely apart, meaning there is no giant set of nodes that can connect to each other with any fidelity. Also shown are the critical mean resource number ${n}_{c}/\ln N$ for which the discontinuous phase transition is avoided.

Quantum scale-free networks

These observations lead to a natural question about how general our results are—especially in terms of the network model. As such it is useful to explore the scale-free Barabási-Albert quantum network whose classical counterpart is known to be more robust than the Erdős-Rényi^25,42,43. In scale-free networks, the degree distribution follows a power law at least asymptotically. This promotes the existence of hub nodes with a degree much larger that the average one (see Fig. 1a for an example). Such distribution is observed in a diverse types of real-world networks²⁷. The Barabási-Albert model⁴⁴ is a simple example that allows us to generate and explore scale-free networks, based on the preferential attachment principle. This means that when links are added to the network they disproportionately connect to nodes with higher degrees²⁷. In Fig. 5(a, b) we plot the operational distance l^op(p^op) and the diameter of connected component D(p^opp^ext) versus the probability a link is operational and not removed p = p^opp^ext for various network sizes N. Our results for the Barabási-Albert network show that we are in the supercritical regime for much lower values of p^ext, which highlights its ability to distribute entanglement even when a large number of links fail. This is to be expected, the Barabási-Albert network, and other scale-free networks, are known to be more robust than an Erdős-Rényi network^43,44. More importantly in Fig. 5c we observe no discontinuous phase transition in the N = 10³–10⁵ region (unlike what occurred in the Erdős-Rényi situation Fig. 3, and therefore there is only one critical probability of links not failing ${p}_{{{{{{{{\rm{c1}}}}}}}}}^{{{{{{{{\rm{ext}}}}}}}}}={p}_{{{{{{{{\rm{c2}}}}}}}}}^{{{{{{{{\rm{ext}}}}}}}}}={p}_{c}^{{{{{{{{\rm{ext}}}}}}}}}$. This is exemplified in Fig. 5d by the absence of a region where both the subcritical and supercritical are stable solutions of Eq. (3). In fact, one can show that there is always a critical quantum-repeater efficiency α_c such that for an efficiency large than the critical one α < α_c the discontinuous phase transition is suppressed (our network used in Fig. 5a, b, c, d has α_c > 1). It is useful to explore this α_c parameter in a little more detail. When our resources are exponentially distributed, it is straightforward to show (supplementary Note 4 for details) that α_c is given by

$${\alpha }_{c}=\mathop{\min }\limits_{p < {p}_{c}}\frac{d(p)/\ln p}{dD(p)/d(\ln (p))}$$

(4)

which establishes the existence of a sufficient repeater efficiency so that most of the classical behavior is recovered. Despite the suppression of the discontinuous phase transition for α < α_c there are still a few differences between the various quantum cases. Unlike what one expects for a typical Barabási-Albert network ^25,43 the point at each of the networks breaks apart, does not change significantly with the network size. To understand this, it is useful to look at the relation between ${p}_{c}^{{{{{{{{\rm{ext}}}}}}}}}$ and the classical percolation critical probability p_c (which for the usual Barabási-Albert network tends to zero as N increases). When our resources are exponentially distributed, ${p}_{c}^{{{{{{{{\rm{ext}}}}}}}}}$ (or ${p}_{c2}^{{{{{{{{\rm{ext}}}}}}}}}$ for a discontinuous phase transition) is related to the classical percolation critical value p_c by, (see Supplementary Note 5 and Fig. S3. for details)

$${p}_{c({c}_{2})}^{{{{{{{{\rm{ext}}}}}}}}}={({p}_{c})}^{\frac{{\left({D}_{\max }\right)}^{\alpha }}{\left\langle n\right\rangle }},$$

(5)

with ${D}_{\max }$ being the critical network diameter, defined as the diameter of the network at the classical phase transition point ${D}_{\max }\mathop{=}\limits^{{{{{{{{\rm{def}}}}}}}}}D({p}_{c})$. This provides quite an interesting insight into this apparent change of behavior. It is well known that the classical percolation critical value p_c tends to zero with the network size for the Barabási-Albert network⁴³, but so does ${D}_{\max }$ (this is what prevents the suppression of the phase transition). This means that the decrease of ${p}_{c({c}_{2})}^{{{{{{{{\rm{ext}}}}}}}}}$ can be mitigated by increasing the average degree of the network $\left\langle n\right\rangle$ proportionally with the critical network diameter to the power of α, ${({D}_{\max })}^{\alpha }$.

Fig. 5: Robustness of a quantum Barabási-Albert network.

Exploration of bond percolation on a quantum Barabási-Albert network with N nodes and average degree c = 6 where the number of entangled pairs in each link follow an exponential distribution with mean 〈n〉. We simulated the the Bollobás variant of the Barabási-Albert model⁴⁹ where we generated one Barabási-Albert network for each value of N. The diameter of the network D(p) was then determined by removing link from the network with probability 1 − p^ext, based on 100 runs for each value of p. We plot the operational distance l^op(p^op) and the network diameter D(p) versus the probability that links are both operational and not removed p = p^opp^ext for $\langle n\rangle ={(10\ln (N))}^{\alpha }$ with α = 1 in a with the large colored dots indicating their intersection. Labelled are the curves Labelled are the curves l^op(p^op) for ${p}^{{{{{{{{\rm{ext}}}}}}}}}={p}_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{{\rm{ext}}}}}}}}}$ which correspond to the smallest value of p indicating a stable l^op(p^op) = D(p^opp^ext) solution. The intersection between two nodes at p₀, is marked by blue dots for solutions in the supercritical regime, and red dots in the subcritical regime. Next the size of the backbone (number of nodes in the backbone) is plotted as a function of p in b. For each intersection point found in a there is a corresponding size in b. In c the size of the backbone is plotted as a function of the probability that links are not removed p^ext. The functionally supercritical regime is represented as the blue region while the functionally subcritical regime is shown as the light red region. The dark red region on the other hand represents the structural subcritical region for a network of size N = 10⁵. We immediately observe that no discontinuous phase transition is seen (unlike in the Erdős-Rényi case). Finally in d we depict the phase diagrams of $\langle n\rangle /\ln N$ versus y for N = 10⁵ nodes including the curves for the critical probabilities ${p}_{c}^{{{{{{{{\rm{ext}}}}}}}}}$ and p_c. Shaded region around each curve represents the standard deviation of the same.

Measuring the robustness of complex networks

Our exploration of the Erdős-Rényi and scale-free Bollobás quantum networks has highlighted how the topology of those networks plays a significant role in its robustness, meaning the ability to distribute entanglement in the presence of link failures, but how? We need to quantify this behavior using three important characterization parameters. The first two parameters are related to how many links need to be removed before the network breaks apart while the third is associated with the efficiency of the repeater protocol. These three parameters can be determined for both the Erdős-Rényi network and Barabási-Albert networks. It is also useful to determine these parameters for geometric networks. In a geometric network, nodes are distributed across a geometric space, and nodes that are closer are more likely to be connected than nodes further apart. This type of model is very natural in quantum communication networks, given the fact that direct quantum links spanning large distances are difficult to generate. We consider two types of geometric networks, geometric graphs⁴⁵, where only nodes that are closer than a certain radius are connected to each other, and the Waxman model where the probability p_ij that two nodes connect to each other decays exponentially with the distance⁴⁶ as ${p}_{ij}=\beta {e}^{-\frac{{r}_{ij}}{R}}$, with r_ij being the distance between node i and j, and R the average connection distance, and in our work we considered β = 1. Although we can describe these networks as a function of the number of nodes and links, for the geometric networks these parameters are associated with physical dimensions⁴⁵. To give an example, a random geometric graph with a connecting radius of 266 km, an average degree c = 6, and a total number of 10³ nodes correspond to a network spanning a physical distance on the order of 10³ km. This conversion is explained in detail in supplementary Note 4 and displayed on the top axis of Fig. 6. With these four network topologies in mind—Erdős-Rényi, Barabási-Albert, geometric random graphs and Waxman model—we plot in Fig. 6 the classical percolation critical probability p_c, ${D}_{\max }$, and α_c versus N, for values of average degree c = 6, 8, 10. Our plots clearly show that scale-free networks are more robust according to all three parameters, that it is the only network that for the selected parameters is able to avoid the discontinuous phase transition for α > 1 with N > 10³. The reasons for this are as follows. The classical percolation critical probability p_c is the typical measure of the robustness of a network in the Bernoulli-percolation model. Scale-free networks are known to be extremely robust against random failures in the Bernoulli-percolation model as the hubs keep the network connected even when a large fraction of links are missing²⁷. In contrast, the geometric random graphs seem to be the less robust networks according to this parameter. The lack of links connecting distant parts of the network hinders their robustness against random failures. Erdős-Rényi and scale-free networks are both small-world networks, meaning the distances between nodes in these networks grow with the logarithm of the number of nodes, and scale-free networks are something called ultrasmall networks because their network distances tend to be even lower²⁷. On the other hand, geometric network models tend not to be small-world⁴⁵. As expected the critical distance ${D}_{\max }$ is lower for the scale-free network and largest for the geometric networks. Scale-free networks are also more robust than other networks in terms of the critical quantum-repeater efficiency α_c. This can be explained by the fact that α_c depends on how the diameter of the network changes when links are removed from the network, Eq. (5). It can be seen from Fig. 3, and Fig. 4 that the diameter of the scale-free network grows considerably slower than that of an Erdős-Rényi network, explaining why this is the case. The diameters of the Waxman and geometric random graphs show similar behavior to the Erdős-Rényi network when nodes are removed. Quantum networks based on capacity channel upper-bounds^15,16, can be seen as a special case of our model when the quantum-repeater efficiency is set to α = 0, a regime in which classical percolation tools can be used, and therefore there are no discontinuous phase transitions. Our results show the importance that the quantum-repeater protocol efficiency plays in a quantum internet, and the importance of choosing the right network topology to mitigate such effects. It is possible, however, to recover the classical behaviors for quantum networks with any topology and sizes for quantum repeaters that operate with α = 0. Realistically, it is unlikely that the first generations of quantum-repeaters networks will be close to that regime, especially when local gate inefficiencies are included. Our results provided a lower, and therefore more practical, threshold for the quantum efficiency required for the construction of a robust network.

There is one more important consideration we must address here in terms of the generality of our results. This relates to our choice of an exponential resource distribution used throughout the paper. The exponential resource distribution was primarily chosen for the ease of our calculations. Other distributions, uniform, for instance, show similar network behavior and our conclusion about the robustness of the Barabási-Albert networks remains unchanged (see Supplementary Note 4 for details). The form of the quantum repeaters, their operation, and how engineers of the future quantum Internet distribute resources throughout the network will determine what the resource distribution actually is. It is still an open question as to what the optimal resource distribution actually would be.

Fig. 6: Robustness of the network as a function of its topology.

Shown are the three critical parameter the critical classical quantum-repeater efficiency, α_c, the critical classical percolation probability, p_c, and the critical network diameter ${D}_{\max }$. The critical classical quantum-repeater efficiency α_c is the required quantum-repeater efficiency necessary to avoid the phase transition for a given network. The classical critical percolation probability, p_c in the minimum probability that a link is not removed, in order to have the network in the connected regime. The relation between the critical classical percolation probability in our model ${p}_{c({c}_{2})}$ and the classical critical percolation probability, p_c depends on the third parameter the critical network diameter ${D}_{\max }$, see Eq. ((5)). The critical network diameter ${D}_{\max }$ is the diameter of the network at the phase transition point. In the left, center, and right panel these are shown for the Erdős-Rényi (ER), Barabási-Albert (SF) geometric graphs (rgg), and the Waxman networks for N varying between 10^2.5–10⁵. For a network to be robust we want α_c and p_c to be as large as possible with ${D}_{\max }$ to be as small as possible. We estimate the parameters above based on 100 network realization for each network model and value of c. For each network D(p) was computed based on 100 runs. Error bars show the standard deviation associated with each estimation. Show in the upper axis is estimation of the order of magnitude for physical range of the two geometric network (rgg and Waxman) assuming a connecting radius of 266 km (see Supplementary Note 6 and Note 7, and Table S1).

By introducing the quantum backbone, we derived a metric to measure the connectivity of a quantum network, and have shown how large-scale quantum networks based on noisy quantum-repeater nodes connected by noisy channels are prone to discontinuous phase transitions. This abrupt behavior breaks the network into disconnected pieces, severely limiting its operational reach. We found that the discontinuous phase transitions can be suppressed if the efficiency of the quantum-repeater protocol is above a certain value that depends on the topology and size of the network, α_c. Furthermore, we have shown that the robustness of a quantum network can be fully characterized using three parameters, the classical percolation critical probability p_c, the critical network diameter ${D}_{\max }$ and the critical quantum-repeater efficiency necessary to avoid the first-order phase transition, α_c. Our results capture an inherent fragility that geometric networks possess, they tend to be more fragile than other networks. On the other hand, scale-free networks are more robust than all other networks according to these three parameters, and the required quantum-repeater efficiency necessary to avoid the first=order transition is not too large. We have shown that the right network topology combined with advanced repeater architectures⁴⁷ provide potential solutions for the realization of robust quantum networks. Nevertheless, it does not mean a scale-free network will be sure of a feasible topology for a quantum network.

Discussion

One of the key requirements to generate a scale-free network in geometric spaces is the existence of direct links spanning long distances. As it as been mentioned before, those are problematic to generate for a quantum network. A combination of short links using optical fiber, and long links using communication through satellite might be enough to generate a scale-free-like quantum network, but more research needs to be done in this regard. Our work also does not consider multi-path purification protocols given the fact that they are still in their infancy. Multi-path purification protocols could be an interesting way to increase the reach of our network, but further research on this type of protocol would be required before we can perform analyses. Finally, it has been shown that scale-free networks although robust against target attacks can be very fragile against target attacks²⁷. This phenomenon was also reported to be present in quantum networks¹⁵. Our model does not say anything about how robust these networks are against random attacks, and it would be an interesting question to address in future work. Our results provide a guiding principle for the design and development of a robust large-scale quantum Internet, at least against random failures, and provide a framework that can be generalized to study another type of failures or attacks.