Introduction

A network has three basic sub-structures: chain, star, and cycle. Chains are closely related to the concept of average distance, whereas a small average distance and a large clustering coefficient together signify a small-world network1, where the clustering coefficient is determined by the number of triangles, which are special cycles. Stars follow some heterogeneous degree distribution, under which the growth of node numbers and a preferential attachment mechanism together distinguish a scale-free network2 from a random network3. Cycles not only contain triangles but also have deeper and more complicated connotations. The cycle structure brings redundant paths into the network connectivity, creating feedback effects and higher-order interactions in network dynamics.

In [4], we introduced the notion of totally homogeneous networks in studying optimal network synchronization, which are networks with the same node degree, same girth (length of the smallest cycle passing the node in concern), and same path-sum (sum of all distances from other nodes to the node). We showed4 that totally homogeneous networks are the ones of easily self-synchronizing among all networks of the same size. Recently, we identified5 the special roles of two invariants of the network topology expressed by the numbers of cliques and cavities, the Euler characteristic number (alternative sum of the numbers of cliques of different orders), and the Betti number (number of cavities of different orders). In fact, higher-order cliques and smallest cavities are basic components of totally homogenous networks.

More precisely, higher-order cycles of a connected undirected network include cliques and cavities. A clique is a fullyvconnected sub-network, e.g., a node is a 0-clique, an edge is a 1-clique, a triangle is a 2-cliques, and a complete graph of four nodes is a 3-clique, and so on, where the numbers indicate the orders. Also, a triangle is the smallest first-order cycle, which consists of three edges. The number of 1-cycles with different lengths (number of edges) is huge in a large-scale network. Similarly, a 3-clique is the smallest two-cycle, and a two-cycle contains some triangles. A chain is a broken cycle, where an edge is the shortest 1-chain, a triangle and two triangles adjacent by one edge are two-chains, and so on, whereas a cycle is a closed chain. In the same manner, all these concepts can be extended to higher-order ones.

It is more challenging to study network cycles than node degrees; therefore, new mathematical concepts and tools are needed6,7, including such as simplicial complex, boundary operator, cyclic operation, and equivalent cycles, to classify various cycles and select their representatives for effective analysis and computation.

In higher-order topologies, the addition of two k-cycles, c and d, is defined5 by set operations as c + d = (c ∪ d) − (c ∩ d). They are said to be equivalent, if c + d is the boundary of a (k + 1)-chain5. All equivalent cycles constitute an equivalent class. The cavity is a cycle with the shortest length in each independent cycle-equivalent class (see ref. 5 for more details).

Cycles, cliques, and cavities are found to play important roles in complex systems such as biological systems especially the brain. In the studies of the brain, computational neuroscience has a special focus on cyclic structures in neuronal networks. It was found8 that cycles generate neural loops in the brain, which not only can transmit information all over the brain but also have an important feedback function. It was suggested8 that such cyclic structures provide a foundation for the brain functions of memories and controls. Unlike cliques, which are placed at some particular locations (e.g., cerebral cortexes), cavities are distributed almost everywhere in the brain, connecting many different regions together. It is pointed out9 that in both biological and artificial neural networks, one can find huge numbers of cliques and cavities which, despite being large and complex, have not been explored before. Of particular importance is that cavities play an indispensable role in brain functioning. All these findings indicate an encouraging and promising direction in brain science research. However, it remains unclear as to how all such neuronal cliques and cavities are connected and organized. This calls for a further endeavor into understanding the relationship between the complexity of higher-order topologies and the complexity of intrinsic neural functions in the brain. To do so, however, it is necessary to find most, if not all, cliques and especially cavities of different orders from the neuronal network.

Artificial intelligence, on the other hand, relies on artificial neural networks inspired by the brain neuronal network10, including recurrent neural networks, convolutional neural networks, Hopfield neural networks, etc. Now, given the recent discovery of higher-order cliques and cavities in the brain, the question is how to further develop artificial intelligence to an even higher level by utilizing all the new knowledge about brain topology. Notably, an effective neuronal network construction was recently proposed by a research team from the Massachusetts Institute of Technology, inspired by the real structure of the neuronal network of the Caenorhabditis elegans11.

It is important to understand how the brain stores information, learns new knowledge, and reacts to external stimuli. It is also essential to understand how the brain adaptively creates topological connections and computing patterns. All these tasks depend on in-depth studies of the brain neuronal network. Recently, the Brain Initiative project of USA (https://en.wikipedia.org/wiki/BRAIN_Initiative, https://braininitiative.nih.gov/), the Human Brain project of EU (https://en.wikipedia.org/wiki/Human_Brain_Project, https://www.humanbrainproject.eu/en/) and the China Brain project (https://en.wikipedia.org/wiki/China_Brain_Project) have been established to take such big challenges.

Many renowned mathematicians had contributed a lot of fundamental work to related subjects, such as Euler characteristic number, Betti number, groups of Abel and Galois, higher-order Laplacian matrices, as well as Euler-Poincaré formula and homology. This also demonstrates the importance of studying cliques and cavities for the further development of network science. In addition, the advance from pairwise interactions to higher-order interactions in complex system dynamics requires the knowledge of higher-order cliques and cavities of networks12. The numbers of zero eigenvalues of higher-order Hodge-Laplacian matrices are equal to the corresponding Betti numbers, while their associate eigenvectors are closely related to higher-order cavities13.

Motivated by all the above observations, this paper studies the fundamental issue of computability of a complex network, based on which the investigation continues to find higher-order cliques and their Euler characteristic number, as well as all the Betti numbers and higher-order cavities. The proposed approach starts from k-core decomposition14 and, through finding cliques of different orders, performs a sequence of computations on the ranks of the corresponding boundary matrices, to obtain all the Betti numbers. To that end, an optimized algorithm is developed for finding higher-order cavities. Finally, the optimized algorithm is applied to computing the neuronal network of C. elegans from a typical data set, identifying its cliques and cavities of different orders.

Results

For computable undirected networks, the proposed approach is able to find all higher-order cliques, thereby obtaining the Euler characteristic number and all Betti numbers as well as some cavities of different orders. These can provide global information for understanding and analyzing the relationships between topologies and functions of various complex networks such as the brain neuronal network.

Computable networks

For undirected networks, the cliques and their numbers of different orders in a network are both important sub-networks and parameters for analysis and computation. A simple example is shown in Fig. 1, from which it is easy to find all cliques and their numbers of different orders.

Fig. 1: A sample network.
figure 1

This network has 14 nodes, 26 edges, 13 triangles, and 1 tetrahedron, where the numbers are node indexes (see ref. 5).

Full size image

For a given general large-scale complex network, however, finding all cliques of different orders is never an easy task. In fact, even just searching for a maximum clique (namely, a clique with the largest possible number of nodes) from a large network is a computationally NP-complete problem15. It is well known that to find all cliques of a large-scale undirected network, especially when the network is dense, the number of cliques is huge and will increase exponentially as the network size becomes larger. For example, in the real USair, Jazz, and Yeast networks16, if the number of cliques is limited to not >107 to be computable on a personal computer, the orders of the cliques are found to be only 9, 6, and 4, respectively, as summarized in Table 1. For these three real-world examples, it becomes impossible to compute the numbers of their higher-order cliques.

Table 1 Three real networks: their sizes (number of nodes |N| and number of edges |E|), maximum coreness kmax, the maximum number of cliques cmax, number of k-cliques mk, and the maximum order k of cliques with their numbers mk < 107.
Full size table

It is noticed that, even for large and dense networks, k-core decomposition can be used to efficiently determine their cells (layers), where the kth cell has all nodes with degrees at least k, and the kernel of the network has the largest coreness value and is very dense. Therefore, the largest coreness value kmax can be used to estimate the order of a maximum clique. For this reason, k-core decomposition is used to determine whether a given network is computable or not, subject to the available limited computing resources. If the computing resources allow the number of cliques, with the first several lowest orders, to be no >107 to be computable, then the maximum coreness value should not be bigger than 30. In this paper, this coreness value threshold is set to kmax = 25, as detailed in Supplementary Note 1.

Clique-searching method

The Bron–Kerbosch algorithm17 is a popular scheme for finding all cliques of an undirected graph, whereas the Hasse-diagram algorithm9 is useful for finding all cliques of a directed network. For computable networks, we propose a method with an algorithm, named the common-neighbors scheme, which can find all cliques of different orders and the associate Euler characteristic number.

In a network, the average degree is denoted by 〈k〉 and the number of edges by |E|. The computational complexity of the proposed algorithm is estimated to be O(|E|〈k〉) for finding all 2-cliques.

For illustration, the sample network shown in Fig. 1 is used for clique searching, with a procedure in six steps, as follows:

  1. (1)

    For each node, all its neighbors are listed, whose index numbers are bigger than the index number of this node:

    Node 1 {2, 3, 4, 5}, Node 2 {3, 4, 5}, Node 3 {4, 6, 8}, Node 4 {Ø}, Node 5 {9}, Node 6 {7, 14}, Node 7 {8}, Node 8 {Ø}, Node 9 {10, 11, 12, 13}, Node 10 {11, 13, 14}, Node 11 {12, 14}, Node 12 {13, 14}, Node 13 {14}, Node 14 {Ø}.

    Then, the number of nodes in 0-clique is computed, yielding m0 = 14.

  2. (2)

    From the above list, edges are generated in increasing order of node indexes:

    (1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 6), (3, 8), (5, 9), (6, 7), (6, 14), (7, 8), (9, 10), (9, 11), (9, 12), (9, 13), (10, 11), (10, 13), (10, 14), (11, 12), (11, 14), (12, 13), (12, 14), (13, 14).

    Then, the number of edges in 1-clique is computed, yielding: m1 = 26.

  3. (3)

    For every edge, if its two end-nodes have a common neighbor whose index number is bigger than the index numbers of the two end-nodes, then all such neighbors are listed. For example:

    edge (1, 2) has common neighbors {3, 4, 5}, edge (1, 3) has {4}, edge (2, 3) has {4}, edge (9, 10) has {11, 13}, edge (9, 11) has {12}, edge (9, 12) has {13}, edge (10, 11) has {14}, edge (10, 13) has {14}, edge (11, 12) has {14}, edge (12, 13) has {14}.

    However, edge (1, 4) and edges (1, 5), (3, 4), (3, 6), (3, 8), (5, 9), (6, 7), (6, 14), (7, 8), (9, 13), (10, 14), (11, 14), (12, 14), (13, 14) do not have any common neighbor. Thus, the following triangles are obtained:

    (1, 2, 3), (1, 2, 4), (1, 2, 5), (1, 3, 4), (2, 3, 4), (9, 10, 11), (9, 10, 13), (9, 11, 12), (9, 12, 13), (10, 11, 14), (10, 13, 14), (11, 12, 14), (12, 13, 14).

    Then, the number of triangles in 2-cliques is computed, yielding: m2 = 13.

  4. (4)

    For each triangle, if its three nodes have a common neighbor whose index number is bigger than the index numbers of three nodes, then all such neighbors are listed.

    Here, only the triangle (1, 2, 3) has a common neighbor, {4}, yielding 1 tetrahedron, (1, 2, 3, 4).

    Then, the number of tetrahedrons in 3-cliques is computed, yielding: m3 = 1.

  5. (5)

    The above procedure is continued until it does not yield any more higher-order clique.

  6. (6)

    Finally, the Euler characteristic number is computed, as follows5:

$$\chi = m_0 - m_1 + m_2 - m_3 = 14 - 26 + 13 - 1 = 0.$$

Computing Betti numbers

The above-obtained cliques of various orders can be used to generate boundary matrices Bk, k = 1, 2, …. Here, B1 is the node-edge matrix, in which an element is 1 if the node is on the corresponding edge; otherwise, it is 0. Similarly, B2 is the edge-face matrix, in which an element is 1 if the edge is on the corresponding face (triangle); otherwise, it is 0. All higher-order boundary matrices Bk are generated in the same way. It is straightforward to compute the rank rk of matrices Bk for k = 1, 2, …, using linear row-column operations in the binary field, following the binary operation rules, namely 1 + 1 = 0, 1 + 0 = 1, 0 + 1 = 1, 0 + 0 = 0. Then, the Betti numbers5 can be obtained by using formulas βk = mk−rk−rk+1, for k = 1, 2, ….

One can also calculate the numbers of zero eigenvalues of higher-order Hodge-Laplacian matrices, so as to find the Betti numbers. To do so, some algebraic topology rules are needed to form oriented cliques13.

As an example, the left-hand sub-network shown in Fig. 1 is discussed, which has Nodes 1–8. The node-edge boundary matrix B1 of rank r1 = 7 is formed as follows, where the first row is linearly dependent on the other rows:

$$\begin{array}{*{20}{c}}\!\!\! {B_1} \; {\begin{array}{*{20}{l}} {\left( {1,2} \right)} \hfill & {\left( {1,3} \right)} \hfill & {\left( {1,4} \right)} \hfill & {\left( {1,5} \right)} \hfill & {\left( {2,3} \right)} \hfill & {\left( {2,4} \right)} \hfill & {\left( {2,5} \right)} \hfill & {\left( {3,4} \right)} \hfill & {\left( {3,6} \right)} \hfill & {\left( {3,8} \right)} \hfill & {\left( {6,7} \right)} \hfill & {\left( {7,8} \right)}\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\qquad\;\; \hfill \end{array}} \\ {\begin{array}{*{20}{l}} 1 \hfill \\ 2 \hfill \\ 3 \hfill \\ 4 \hfill \\ 5 \hfill \\ 6 \hfill \\ 7 \hfill \\ 8 \hfill \end{array}} {\left( {\begin{array}{*{20}{l}} 1 \qquad\hfill & 1 \qquad\hfill & 1 \qquad\hfill & 1\quad \hfill & 0\quad \hfill & 0 \quad\hfill & 0 \quad\hfill & 0 \qquad\hfill & 0 \qquad\hfill & 0 \qquad\hfill & 0 \qquad\hfill & 0 \hfill \\ {\bf1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {\bf 1} \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\bf 1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {\bf 1} \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\bf 1} \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\bf 1} \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\bf 1} \hfill & 0 \hfill & 1 \hfill \end{array}} \right)}\qquad\qquad\;\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \end{array}$$

Moreover, its edge-face boundary matrix of rank r2 = 4 is obtained as follows, where the rightmost column (column (2, 3, 4)) is linearly dependent on the other columns:

$$\begin{array}{*{20}{c}}\!\!\!\!\!\!\! {B_2} \quad\;\;\; \!{\begin{array}{*{20}{l}} \!\!\!\!\quad{\left( {1,2,3} \right)} \hfill & {\left( {1,2,4} \right)} \hfill & {\left( {1,2,5} \right)} \hfill & {\left( {1,3,4} \right)} \hfill & {\left( {2,3,4} \right)} \hfill \end{array}} \\ {\begin{array}{*{20}{l}} (1,2) \hfill \\ (1,3) \hfill \\ (1,4) \hfill \\ (1,5) \hfill \\ (2,3) \hfill \\ (2,4) \hfill \\ (2,5) \hfill \\ (3,4) \hfill \end{array}}\, \!\!\!\!\quad{\left( {\begin{array}{*{20}{c}} \;\;\;1\hfill \;\quad\qquad & \!\!\!\!\!1 \qquad\;\; \hfill & 1 \qquad\;\!\!\hfill & \;\; 0 \qquad\;\;\!\hfill & 0 \qquad\\ \;\;\;1 \hfill & \!\!\!\!\!0 \hfill & 0 \hfill & \;\;1 \hfill & 0 \hfill \\ \;\;\;0 \hfill & \!\!\!\!\!1 \hfill & 0 \hfill & \;\;1 \hfill & 0 \hfill \\ \;\;\;0 \hfill & \!\!\!\!\!0 \hfill & 1 \hfill & \;\;0 \hfill & 0 \hfill\hfill \\ \;\;\;{\bf1} \hfill & \!\!\!\!\!0 \hfill & 0 \hfill & \;\;0 \hfill & 1 \hfill\\ \;\;\;0 \hfill & \!\!\!\!\!{\bf1} \hfill & 0 \hfill & \;\;0 \hfill & 1 \hfill\\ \;\;\;0 \hfill & \!\!\!\!\!0 \hfill & {\bf1} \hfill & \;\;0 \hfill & 0 \hfill\\ \;\;\;0 \hfill & \!\!\!\!\!0 \hfill & 0 \hfill & \;\;{\bf1} \hfill & 1 \hfill\end{array}} \right)} \end{array}$$

Table 2 summarizes all calculation results of the network shown in Fig. 1, in which the Euler characteristic number and Betti numbers satisfy the Euler-Poincaré formula5

$$\chi = \beta _0 - \beta _1 + \beta _2 - \beta _3 = 1 - 2 + 1 - 0 = 0$$
Table 2 Computational results of the network are shown in Fig. 1.
Full size table

Cavity-searching method

The concept of cavity comes from the homology group in algebraic topology. As a large-scale network has many 1-cycles, for instance, the network shown in Fig. 1 has hundreds, to facilitate investigation they are classified into equivalent classes. In a network, each 1-cavity belongs to a linearly independent cycle-equivalent class5 with the total number equal to the Betti number β1. It is relatively easy to understand 1-cavity, which has boundary edges consisting of 1-cliques. Imagination is needed to understand higher-order cavities, which have boundaries consisting of some higher-order cliques of the same order. In the literature, only one two-cavity consisting of eight triangles is found and reported8. In this paper, we found all possible smallest cavities and list them up to order 11 in Supplementary Note 2.

Since a cavity belongs to a cycle-equivalent class, only one representative from the class with the shortest length (namely, the smallest number of cliques) is chosen for further discussion. To find the smallest one, however, optimization is needed.

Finding cavity-generating cliques

The procedure is as follows.

First, a maximum linearly independent group of column vectors is selected from the boundary matrix Bk, used as the minimum kth-order spanning tree, which consists of rk k-cliques, where rk is the rank value of the boundary matrix Bk discussed above. Then, linear row-column binary operations are performed to reduce it to be in the simplest form. In every row of the resultant matrix, the column index of the first nonzero element is used as the index of the k-clique in the spanning tree. As an example, for the sub-network with Nodes 1–8 on the left-hand side of the network shown in Fig. 1, the bold-faced 1’s in matrix B1 correspond to the columns indicated by (1, 2), (1, 3), (1, 4), (1, 5), (3, 6), (3, 8), (6, 7) shown at the top of the matrix, which constitutes a spanning tree in the sub-network with Nodes 1–8 in Fig. 1. It should be noted that the minimum kth-order spanning trees are not unique in general.

Next, the maximum group of linearly independent column vectors from boundary matrix Bk+1 is found, obtaining rk+1 (k + 1)-cliques as a group of linearly independent cliques. From this group, one continues to search for a k-clique that belongs to the boundary of the (k+1)-clique but does not belong to the kth-order spanning tree. In other words, the rk+1 k-cliques should not be a k-clique in the minimum spanning tree. If this cannot be found, then one can choose another maximum group of linearly independent column vectors from boundary matrix Bk+1 and search again. In this way, rk+1 (k + 1)-cliques are found. As an example, for the sub-network with Nodes 1–8 in Fig. 1, the bold-faced 1’s in the boundary matrix B2 correspond to the edges indicated by (2, 3), (2, 4), (2, 5), (3, 4). These are edges on the left-hand side of the boundary matrix Bk+1, which are different from the cliques in the spanning tree.

Then, the formula of Betti numbers, βk = mk − rk − rk+1, is used for computing, which is the number of linearly independent k-cavities. The task now is to find the rest k-cliques that are not in the kth-order minimum spanning tree and also not on the boundaries of linearly independent (k + 1)-cliques. These are called cavity-generating k-cliques. In the same sub-network example, there is only one such clique: (7, 8). On the minimum spanning tree, after including all linearly independent boundaries, adding any cavity-generating k-clique will create a linearly independent k-cavity; in this example, the created one is the 1-cavity (3, 6, 7, 8).

Searching cavities by 0–1 programming

Every cavity-generating k-clique corresponds to at least one k-cavity. However, a cavity-generating k-clique may correspond to several cavities of different lengths, where the length is equal to the number of cliques. As a cavity is a linearly independent cycle with the smallest number of cliques, the task of searching for a cavity can be reformulated as a 0–1 programming problem.

As shown above, there are mk k-cliques, Bk is the boundary matrix between a (k − 1)-clique and a k-clique, Bk+1 is the boundary matrix between a k-clique and a (k + 1)-clique, and a k-cavity consists of some k-cliques. In the following, the vector space formed by k-cliques is denoted by Ck. A k-cavity can be expressed as \({{{{{{{\boldsymbol{x}}}}}}}} = ( {x_1,\,x_2, \ldots ,\,x_{m_k}}) \in C_k,\) in which each component xi takes value 1 or 0, where 1 represents a k-clique with index i in the cavity, whereas 0 means no such cliques there. Now, a cavity-generating k-clique with index v is taken from all k-cliques and a vector e = (1, 1, …, 1)T is introduced. Then, the problem of searching for a k-cavity becomes the following optimization problem, which is to be solved for a nonzero solution:

$$ \, \mathop{\min}\nolimits_{{{{{{\boldsymbol{x}}}}}} \in C_k}\;f\left( {{{{{\boldsymbol{x}}}}}} \right) = {{{{{\boldsymbol{xe}}}}}}\\ \, {{{{{\mathrm{s}}}}}}{{{{{\mathrm{.t}}}}}}{{{{{\mathrm{.}}}}}}\quad\left( {{{{{\mathrm{i}}}}}} \right)\; x_v = 1\\ \qquad\hskip4pt\left( {{{{{{\mathrm{ii}}}}}}} \right)\; B_k{{{{{\boldsymbol{x}}}}}}^T = 0\left( {{{{{{\mathrm{mod}}}}}}\,2} \right)\\ \qquad\hskip4pt\left( {{{{{{\mathrm{iii}}}}}}} \right)\;{{{{{\mathrm{rank}}}}}}({{{{{\boldsymbol{x}}}}}}^T,\,B_{k + 1})_{{{{{{\boldsymbol{F}}}}}}_2} = 1 + r_{k + 1}.$$
(1)

Here, the first constraint means that the cavity comes from the cavity-generating k-clique with index v. The second constraint implies that the cavity is a k-cycle, namely the boundaries of k-cliques that form the cavity should appear in pairs. The third constraint shows that the k-cavity to be found will not be a linear representation of the (k + 1)-cliques, where F2 indicates that the operations are performed in the binary field, which can avoid generating false cavities.

To ensure that the βk cavities found are linearly independent, the following 0–1 programming is performed, where x(l) is the lth k-cavity: (i) \(x_v^{(l)} = 1\); (ii) \(B_k{\it{x}}^{(l)T} = 0\left( {{{{{{{{\mathrm{mod}}}}}}}}\,2} \right)\); (iii) \({{{{{{{\mathrm{rank}}}}}}}}\left( {x^{\left( 1 \right)T},...,x^{(l)T},B_{k + 1}} \right)_{F_2} = l + r_{k + 1}\), for l = 1, 2, …, βk.

It was found that the sample network in Fig. 1 has two 1-cavities, where two cavity-generating 1-cliques are x14 = 1 corresponding to edge (7, 8) and x11 = 1 corresponding to edge (5, 9). This optimization is detailed as follows:

$$ \, \mathop{\min}\limits_{{{{{{\boldsymbol{x}}}}}} \in C_1}f\left( {{{{{\boldsymbol{x}}}}}} \right) = {{{{{\boldsymbol{xe}}}}}}\\ \, {{{\rm{s.t.}}}}\;\left( {{{\rm{i}}}} \right)\; x_{14} = 1,\;\left( {{{{\rm{ii}}}}} \right)\; B_1x^T = 0\;\left( {{{{\mathrm{mod}}}}\;2} \right),\;{{{\mathrm{namely}}}}\\ \quad\;\;\; x_1 + x_2 + x_3 + x_4 = 0,\;x_1 + x_5 + x_6 + x_7 = 0,x_2 + x_5 + x_8 + x_9 + x_{10} = 0,\\ \quad\;\;\; x_3 + x_6 + x_8 = 0,x_4 + x_7 + x_{11} = 0,x_9 + x_{12} + x_{13} = 0,x_{12} + x_{14} = 0,x_{10} + x_{14} = 0,\\ \quad\;\;\; x_{11} + x_{15} + x_{16} + x_{17} + x_{18} = 0,x_{15} + x_{19} + x_{20} + x_{21} = 0,\\ \quad\;\;\; x_{16} + x_{19} + x_{22} + x_{23} = 0,x_{17} + x_{22} + x_{24} + x_{25} = 0,\\ \quad\;\;\; x_{18} + x_{20} + x_{24} + x_{26} = 0,x_{13} + x_{21} + x_{23} + x_{25} + x_{26} = 0,\\ \quad\;\;\; \left( {{{\rm{iii}}}} \right)\;{{{{{\mathrm{rank}}}}}}\;({{{{{\boldsymbol{x}}}}}}^T,\;B_2)_{{{{{{\boldsymbol{F}}}}}}_2} = 1 + r_2.$$
(2)

By solving the above 0–1 programming problem, with x14 = 1 corresponding to (7, 8), it yields x10 = 1 corresponding to (3, 8), and with x12 = 1 corresponding to (6, 7), it yields x9 = 1 corresponding to (3, 6), which generates the first cavity (3, 6, 7, 8). Then, replacing x14 = 1 with x11 = 1 yields the second cavity (1, 5, 9, 10, 14, 6, 3), which has 8 equal-length cavities, including 1-cavity (2, 5, 9, 10, 14, 6, 3) and 1-cavity (1, 5, 9, 11, 14, 6, 3), etc. Finally, checking the \({{{{{{{\mathrm{rank}}}}}}}}({{{{{{{\boldsymbol{x}}}}}}}}^{\left( 1 \right)T}, \cdots ,{{{{{{{\boldsymbol{x}}}}}}}}^{(l)T},\,B_2)_{{{{{{{{\boldsymbol{F}}}}}}}}_2} = l + r_2\), for l = 1, 2, verifies that the optimization meets all the constraints.

Cliques and cavities of C. elegans

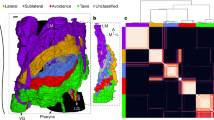
For a data set of C. elegans with 297 neurons and 2148 synapses18, all cliques and some cavities are obtained here by using the above-described techniques and algorithms, which are compared with the Erdös-Rényi (ER) random network with the same numbers of nodes and edges. The results are shown in Fig. 2 and Table 3.

Fig. 2: Cliques and Betti numbers.
figure 2

The number of cliques and the Betti numbers for the C. elegans neuronal network versus the Erdös-Rényi (ER) random network.

Full size image
Table 3 Euler characteristic number, Betti numbers, and the Euler-Poincaré formula for the C. elegans network and the Erdös-Rényi (ER) network.
Full size table

Since the highest-order nonzero Betti number is β3 = 4, the C. elegans has four linearly independent three-cavities, and these four cavities have cavity-generating 3-cliques {164, 163, 119, 118}, {119, 167, 118, 227}, {195, 185, 119, 118} and {227, 195, 119, 118}. The cavity-generating 3-clique {164, 163, 119, 118} forms a three-cavity with eight nodes {85, 13, 3, 164, 163, 119, 118, 158}, which is the smallest three-cavities5, with structures shown in Fig. 3a. The cavity-generating 3-clique {119, 167, 118, 227} forms a three-cavity with 11 nodes {163, 3, 162, 119, 154, 167, 118, 227, 85, 13, 164} as shown in Fig. 3b. The cavity-generating 3-clique {195, 185, 119, 118} forms a three-cavity with eight nodes {171, 13, 3, 195, 185, 119, 118, 173}, as shown in Fig. 3c. The cavity-generating 3-clique {227, 195, 119, 118} forms a three-cavity with eight nodes {173, 13, 3, 227, 195, 119, 118, 185}, as shown in Fig. 3d. All details are included in Supplementary Note 3.

Fig. 3: Four 3-cavities in the C. elegans neuronal network.
figure 3

a 3-cavity with 8 nodes; b 3-cavity with 11 nodes; c 3-cavity with 8 nodes; d 3-cavity with 8 nodes.

Full size image

Discussions

For a given directed network, how can one analyze its higher-order cliques and cavities? In [9], a Hasse algorithm was designed to find all directed cliques. However, both concepts of cycle and cavity were not precisely defined there. For an undirected network, the length of a cavity, namely the number of cliques that compose it, is longer than the lengths of the cliques (the order of the cavity plus 1) as a cycle. For example, an undirected triangle of length 3 not only is a 2-clique but also is a 1-cycle, whereas 1-cavity at least is a quadrangle of length 4. For a directed network, however, this may not be true. For instance, the smallest directed 1-cavity could be composed of two reversely directed edges between two nodes, where both edges have length 2. But, a directed 2-clique could be a directed triangle of length 3. This shows the extreme complexity of directed cavities, which will be a research topic for future investigation.

It should be noted that the key technique used in this paper is to examine various combinations of cliques and cavities, which differs from the studies based on node degrees in the current literature, where the focus is on statistical rather than topological properties of the network. After comparing the neuronal network of C. elegans to a random network, it was found that they are very different regarding the numbers of cliques and cavities. From the perspective of brain science, various combinations of higher-order topological components such as cliques and cavities are of extreme importance, without which it is very difficult or even impossible to understand and explain the functional complexity of the brain. In fact, this provides reasonable supports to many recent studies on the brain12,13,14.

The intrinsic combination of cliques and cavities also brings some unexpected problems to programming the proposed optimization algorithm. For example, because a minimum spanning tree of a network is not unique, the algorithm may not produce the expected results when searching for cavities. Efforts have been made to determine the information of cavities by eigenvectors corresponding to zero eigenvalues of higher-order Hodge-Laplacian matrices. However, a similar non-uniqueness problem occurred in finding eigenvectors, demonstrating the extreme complexity of the clique and cavity-searching problems.

Method and algorithms

To solve the above optimization problem (Eq. (1)) with βk k-cavities is difficult due to the third constraint in the optimization, and because the minimum spanning tree is not unique. As a remedy, the optimization problem is separated into two parts.

The first part is to use the following 0–1 programming to search for all possible cycles that contain the βk k-cavities x(l), l = 1, 2, …, βk:

$$ \, \mathop{\min}\nolimits_{{{{\boldsymbol{x}}}} \in C_k}f\left( {{{\boldsymbol{x}}}} \right) = {{{\boldsymbol{x}}}}^{(l)}{{{\boldsymbol{e}}}}\\ \; {{{\rm{s.t.}}}}\quad ({{{\rm{i}}}})\; x_v^{(l)} = 1;\\ \hskip23pt\, ({{{\rm{ii}}}})\; B_{k} {{{\boldsymbol{x}}}}^{(l)T} = 0 \; ({{{\rm{mod}}}}\; 2)$$
(3)

The second part is to use the third constraint to find all the βk k-cavities within all possible cycles, i.e., to check if \({{{{{{{\mathrm{rank}}}}}}}}(x^{\left( 1 \right)T}, \cdots ,x^{(l)T},B_{k + 1})_{F_2} = l + r_{k + 1}\), for the lth cavity x(l), l = 1, 2, …, βk.

Searching for specific cycles

Because there is a constraint Bkx(l)T = 0 (mod 2) in Eq. (3), it is not a traditional 0–1 linear programming problem. To reformulate the problem, a couple of notations are introduced: \(\tilde B_k = [B_k,\, - 2{{{{{{{\boldsymbol{I}}}}}}}}]\) and \({{{\tilde{\boldsymbol x}}}}^{(l)T} = [{{{{{{{\boldsymbol{x}}}}}}}}^{(l)},\,{{{{{{{\boldsymbol{y}}}}}}}}]\), where I is the identity matrix and \({{{{{{{\boldsymbol{y}}}}}}}} = [y_1, \ldots ,y_{m_k}]\). Then, Bkx(l)T = 0 (mod 2) can be equivalently rewritten as \(\tilde B_k{{{\tilde{\boldsymbol x}}}}^{(l)T} = 0\). As the minimum length of the k-cavity is Lmin = 2k+1, Eq. (3) can be transformed to the following 0–1 programming problem for a linear system of equations:

$$ \, \mathop{\min}\nolimits_{{{{{{\boldsymbol{x}}}}}} \in C_k}f\left( {{{{{\boldsymbol{x}}}}}} \right) = {{{{{\boldsymbol{x}}}}}}^{(l)}{{{{{\boldsymbol{e}}}}}}\\ \,\left( {{{{{\mathrm{i}}}}}} \right)\; x_v^{(l)} = 1,\\ \,\left( {{{{{{\mathrm{ii}}}}}}} \right)\;{{{{{\boldsymbol{x}}}}}}^{(l)}{{{{{\boldsymbol{e}}}}}} = L_{{{\rm{min}}}},\\ \,\left( {{{{{{\mathrm{iii}}}}}}} \right)\; \tilde B_k{{{\tilde{\boldsymbol x}}}}^{(l)T} = 0,\\ \, \left( {{{{{{\mathrm{iv}}}}}}} \right)\; x_i,y_i = 0\; {{{{{\mathrm{or}}}}}}\;1,\;\;l = 1,2, \ldots ,\beta _k.$$
(4)

Equation (4) can be solved by using Matlab toolbox for 0–1 linear system of equations, and the algorithm is described as follows.

Algorithm 1

Searching specific cycles (x* = Find Cycle (Bk, v, Lmin)).

Input: boundary matrix Bk

indices of all cavity-generating cliques {v1, …, \(v^{\beta _k}\)}

length of the smallest cycle Lmin = 2k+1

Output: specific cycles x*

Finding all cavities

The third constraint in the optimization problems (Eqs. (3) and (4)) is needed to check, so as to identify which cycles found by Algorithm 1 are k-cavities and then to determine their cavity-generating cliques. For cavity-generating cliques not included in the list in Algorithm 1, or if there are many cavity-generating cliques appearing in the same cavity, one has to search new cycles obtained by Algorithm 1 again by increasing the lengths of the 2k‒1 cliques.

Summarizing the above steps gives the following cavity-searching algorithm:

Algorithm 2

Checking all k-cavities (\(\{ {{{{{{{{\boldsymbol{x}}}}}}}}_1^ * , \ldots ,{{{{{{{\boldsymbol{x}}}}}}}}_{\beta _k}^ * } \} = {{{{{\mathrm{Find}}}}}}\;{{{{{\mathrm{Cavity}}}}}}\; ( {B_k,\;B_{k + 1},\;v,\;L_{{{{{\rm{min}}}}}}} )\))

Input: boundary matrices \(B_k\) and \(B_{k + 1}\)

indices of all cavity-generating cliques \(\left\{ {v^1, \ldots ,v^{\beta _k}} \right\}\)

length of cycle \(L_{{{{{\rm{min}}}}}} + j2^{k - 1},\;j = 0,\;1, \ldots\)

Output: all k-cavities \(\{ {{{{{{{{\boldsymbol{x}}}}}}}}_1^ * , \ldots ,{{{{{{{\boldsymbol{x}}}}}}}}_{\beta _k}^ * } \}\)