Crowded transport within networked representations of complex geometries

Abstract

Transport in crowded, complex environments occurs across many spatial scales. Geometric restrictions can hinder the motion of individuals and, combined with crowding, can have drastic effects on global transport phenomena. However, in general, the interplay between crowding and geometry in complex real-life environments is poorly understood. Existing analytical methodologies are not always readily extendable to heterogeneous environments and, in these situations, predictions of crowded transport behaviour rely on computationally intensive mesh-based approaches. Here, we take a different approach based on networked representations of complex environments in order to provide an efficient framework to explore the interactions between environments’ geometry and crowding. We demonstrate how this framework can be used to extract detailed information both at the level of the individual as well as of the whole population, identify the environments’ topological features that enable accurate prediction of transport phenomena, and provide insights into the design of optimal environments.

Introduction

The efficacy of a wide range of cellular processes within living organisms, from protein synthesis¹ to the initiation of a T-cell immune response², hinges upon the timely transport of macromolecules through crowded intracellular environments³. The motion of individuals within complex environments is central, but not limited to, cell biology, and is important in a wide range of scientific and technological disciplines. Indeed, understanding the roles that both geometry and crowding play in regulating transport processes has immediate and disparate applications across a vast range of spatial and temporal scales, from designing planning algorithms for autonomous robotic motion⁴ to utilising the transport of nanoparticles to deliver targeted drug therapies⁵. However, despite the ubiquity of applications, a general means to quantify and characterise the relationships between environmental geometry, crowding and transport phenomena in complex real-life environments remain elusive. Mathematical studies such as this one can play a key role in identifying and quantifying such relationships.

The behaviour of crowded individuals has captured the attention of mathematicians and physicists for decades^6,7,8,9, and the environments in which the individuals are constrained to have been found to have large consequences for the emergent transport behaviour. For particles diffusing along an infinite one-dimensional lattice¹⁰, excluded volume interactions between particles significantly hinder the motion of tracer particles and can induce a qualitative shift in the time-dependence of the mean squared displacement (MSD) from classically diffusive (MSD ~ t) to anomalously diffusive (MSD ~ t^α, where α < 1). However, for some fractal environments, including diffusion-limited aggregates, the MSD for a tracer particle has the same exponent both in the presence and absence of crowding¹¹. Moreover, on comb lattices (one-dimensional backbones with periodic and infinite extrusions representing low-dimensional environments) exclusion interactions along the backbone result in a speed-up of the transport of a tracer particle, and even results in super-diffusive behaviour (MSD ~ t^α, where α > 1) on intermediate timescales¹². Crowding in complex environments has also been studied on higher-dimensional (greater than or equal to two) regular lattices, such as diffusion in the presence of obstacles^13,14,15 and crowded transport on Manhattan lattices¹⁶ where environmental complexity arises via disordered directionality in the lattice. The above studies make analytical progress in understanding crowded transport behaviour by utilising symmetry and scaling arguments, as well as exploiting the infinite size of these domains. Whilst less common, there are studies that make analytical progress in understanding crowded transport in finite heterogeneous environments. For example, the transport of proteins within heterochromatin has been studied using results from transport within fractal environments¹⁷. Additionally, analytical results from lattice gas cellular automata models have been used to study cell migration in heterogeneous environments, by coupling the automata to a vector field representing environmental complexity¹⁸. However, when interested in exploring microscopic properties of crowded transport in detailed non-fractal real-life environments, such as the intracellular environment, many of these analytical approaches are not readily extendable. In such situations, sophisticated numerical approaches are employed instead.

Significant technological advances in imaging techniques, such as light-sheet microscopy¹⁹ and x-ray tomography²⁰, have drastically enhanced the availability of high-resolution images of complex environments (see Fig. 1a). Incorporating these detailed geometries into mathematical studies of crowded transport requires discretisation of the geometry into a high-resolution mesh, this is a collection of interconnected voxels upon which transport models can be studied numerically. However, numerically integrating equations of motion on these meshes can incur significant computational costs, particularly for stochastic modelling paradigms that require repeated simulations to explore expected transport behaviour^21,22,23. If these computational costs are too high they present a barrier to studying a large ensemble of geometries, as is necessary to properly characterise how geometry and crowding influences transport behaviour. In addition, it remains unclear how to relate such high-dimensional descriptions of the geometry with statistics of the transport process in order to fully understand the relationship between geometry and crowded transport.

Fig. 1: Complex environments and their networked representations.

a An electron-microscopy image highlighting the substructures within a cardiomyocyte cell. The highlighted dark grey regions are mitochondria which act as barriers to macromolecular transport. This image was provided by the Cell Structure and Mechanobiology Laboratory at the University of Melbourne. b The free space within a subsection of the cardiomyocyte is segmented into five distinct reservoirs, connected by narrow channels highlighted in red. c The natural networked topology arising from the cell segmentation. d Macromolecules (small circles) experience stronger crowding effects within the narrow channels.

Circumventing the limitations of high-resolution meshes requires a framework for studying crowded transport in complex environments that avoids traditional spatial discretisation methods. A proposed alternative description of complex geometries is to represent the geometry as a network^24,25,26. In particular, geologists have used these networked representations to study the transport of fluid and sediment through porous media²⁷. There are several available algorithms (such as the maximal ball algorithm²⁵ and SNOW²⁶) to extract networked representations that initially dissect complex geometries into several reservoirs (see Fig. 1b). Connecting these reservoirs are narrow regions of space that are referred to as throats. These throats represent highly restricted regions where individuals experience strong crowding, as seen within heterogeneous porous media²⁷, nanotubes in microfluidic devices²⁸, and in newly discovered nanotunnels that connect mitochondria²⁹. Networks are formed by assigning the reservoirs to be the network nodes, and an edge connects two nodes if the corresponding reservoirs are connected by a throat. The reservoirs are often described as balls with a volume equal to the volume of the reservoir, this leads to what is referred to as a balls and sticks network (Fig. 1c). By virtue of the fact that the reservoirs are typically much larger than a voxel in a mesh reconstruction (Fig. 1c), such networks provide a low-dimensional, efficient characterisation of the complex geometry. Indeed, application of a network extraction algorithm (SNOW²⁶) to the cardiomyocyte image in Fig. 1a produces a network with 81 reservoirs, whereas the natural Cartesian mesh (where each pixel is represented as a voxel) has 16,774 voxels (see Supplementary Note 4 and Supplementary Fig. 10).

Beyond dimensionality reduction, networked representations allow one to characterise the role of geometry in regulating transport processes due to the breadth of available topological descriptors that can predict networked transport behaviour^30,31,32. For example, two classes of summary statistics that are known to accurately predict various emergent transport behaviours are degree-based statistics (these depend solely on the degree distribution of the network, where the degree of a node is equal to the number of edges adjacent to that node) and spectral-based statistics (quantities based on the eigendecomposition of network-related matrices, such as the graph Laplacian³³).

Whilst the majority of the literature on networked transport focuses on single non-crowded individuals, there have been several studies exploring crowded transport processes on networks. The totally asymmetric simple exclusion process (TASEP) is a transport process where particles can move only in one direction along one-dimensional segments and individuals cannot bypass each other. The TASEP has been studied extensively on the one-dimensional line³⁴, small graphs^35,36 and large networks^37,38,39, where the uni-directionality of the transport results in various behaviours such as shocks and traffic jams⁴⁰. In addition the TASEP has been used to model, for example, protein dynamics along microtubule networks^41,42. In these models proteins are assumed globally well-mixed within a single large reservoir which is coupled to a filament network upon which the proteins perform asymmetric random walks with exclusion.

In contrast, in this work, we are interested in the unbiased transport of individuals that are locally well-mixed within the reservoirs that make up the network. Moreover, the individuals are purely constrained to the network and experience crowding only within geometrically constrained regions (Fig. 1d). As such we build a mathematical framework to study the transport of individuals on general finite networks (in the form of balls and sticks, Fig. 1d) where crowding effects are present only along the edges of the network.

We introduce our framework for crowded, networked transport by presenting a hierarchy of diffusive transport models with increasing computational scalability (Supplementary Table 1 provides a summary). The ability of our framework to identify governing principles connecting transport, crowding and geometry is demonstrated through an examination of how crowding and topology affect networked equilibration times⁴³. Understanding this relationship is crucial as many results within statistical physics assume an equilibrated population, but the validity of this assumption is rarely addressed⁴⁴. A key result of our work is that heterogeneity in the microscopic structure of complex environments enables low-connectivity networks, as seen in networked descriptions of real-world environments (Fig. 1a–d), to achieve globally minimal equilibration times. We conclude by extending our framework to provide information on the dynamics of a single motile individual, an extension which opens the door to studying the dynamics of intracellular signalling pathways⁴⁵, where the dynamics of individual proteins are known to control a vast range of biological processes, such as T-cell activation and stem cell differentiation.

Results

Individual crowding combined with geometry-induced crowding drastically slows equilibration

A complex environment (Fig. 1a–d) is described by a network ${{{{{{{\mathcal{G}}}}}}}}=\{{{{{{{{\mathcal{V}}}}}}}},{{{{{{{\mathcal{E}}}}}}}}\}$, where ${{{{{{{\mathcal{V}}}}}}}}$ is the set of reservoirs and their connectivity is specified by the set of edges ${{{{{{{\mathcal{E}}}}}}}}$. Each edge represents a narrow channel within the geometry where crowding between individuals is non-negligible (Fig. 1d). To incorporate crowding, a narrow channel $(i,j)\in {{{{{{{\mathcal{E}}}}}}}}$ connecting distinct reservoirs i and j is discretised using a one-dimensional lattice with integer length K_(i,j), where individuals undergo a symmetric random walk and at most one individual may occupy each lattice site (Supplementary Note 3 provides a relaxation of this assumption), this process is known as a symmetric simple exclusion process (SSEP)⁴⁶. Crowded transport within this networked environment is modelled using a canonical framework for stochastic processes, the continuous-time Markov chain (CTMC). A population of N individuals is distributed on the network (Fig. 2c) and their positions evolve as follows. An individual within a narrow channel lattice site attempts to jump into an adjacent lattice site or reservoir at rate α. If the adjacent site is already occupied a collision event occurs and the jump is aborted (Fig. 2a). However, due to the volumetric differences between reservoirs and narrow channels (Fig. 1b) crowding effects in reservoirs are assumed negligible and so jumps into reservoirs are never aborted. Individuals within each reservoir are assumed well-mixed. Those in reservoir i attempt to jump into the first lattice site of one of their connecting narrow channels at rate γ_i (Fig. 2a), this means that ${\tau }_{i}={\gamma }_{i}^{-1}$ is the average time taken for an individual in the ith reservoir to exit the reservoir. This exit time depends strongly on the local geometry of each reservoir^47,48 and can be calculated as follows. To calculate the mean reservoir exit time for a well-mixed individual we can first consider narrow exit time problems, for which both analytical and computational approaches are readily available^48,49,50. Narrow exit times quantify the time taken for a particle to reach a narrow opening (such as the opening of a narrow channel) conditional on the initial position of the individual. Integrating these quantities over the reservoir and normalising by the reservoir volume, will yield mean exit times for well-mixed individuals. However, in the interest of maintaining generality, we keep the parameters τ_i to be abstract, but note particular reservoir geometries can be incorporated as described above. This CTMC is referred to as the full Markov model (FMM) and a formal description is given in the “Methods”, section “Full Markov model”.

Fig. 2: A combination of crowding and geometry can impede population level transport.

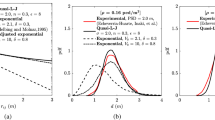
a Diagrammatic representation of the microscopic rules within the narrow channel. The red arrows represent moves that are prohibited due to crowding, the green arrows represent permitted jumps. The parameter γ_i represents the rate at which particles attempt to exit the right-most reservoir. b Equilibration time of the FMM with individual crowding (solid curve) and without (dot-dashed curve) for a three-reservoir network (inset). The equilibration time of the Ornstein–Uhlenbeck process in both the low- and high-density regimes (dashed black curves). The low- and high-density regimes are highlighted in grey. The parameters are K_(1,2) = K_(2,3) = 2, ${{{{{{{\boldsymbol{\tau }}}}}}}}=\delta \left(2,4/3,1\right)$ such that 〈τ〉 = 13δ/9 and 〈τ〉 varies from 10⁻³ to 10⁵, α = 1, and N = 25. c Diagrammatic representation of the full Markov model (FMM) where narrow channels between reservoirs (large circles) are discretised as integer lattices along which individuals (black dots) undergo crowded transport. d Diagrammatic representation of the reduced Markov model (RMM) where individuals hop directly between adjacent reservoirs. The possible hopping directions are indicated by the arrows.

Evaluating how geometry combined with crowding can impact transport behaviour requires a suitable summary statistic with which to characterise transport. Intuitively, it can be reasoned that the effects of crowding between individuals along narrow channels should result in a “slowing down” of the transport process as individuals in the channels block the paths of others. The insightful statistic to quantify such an effect is the time taken for an initially unequilibrated population of individuals to become well-mixed. This time is known as the equilibration time and is calculated as the reciprocal of the spectral gap (second smallest eigenvalue in absolute value) of the transition matrix for the CTMC⁵¹. The average reservoir mean exit time, $\langle {{{{{{{\boldsymbol{\tau }}}}}}}}\rangle =\left(\mathop{\sum }\nolimits_{i = 1}^{| {{{{{{{\mathcal{V}}}}}}}}| }{\tau }_{i}\right)/| {{{{{{{\mathcal{V}}}}}}}}|$, quantifies the time for an individual to attempt to leave the average reservoir. As the individual τ_i are dictated by the geometry of each reservoir, the average reservoir mean exit time is a global geometric descriptor of the complex environment. We note that considering higher-order moments of the reservoir exit time would reveal higher-order geometric effects, however, these cannot be incorporated in a Markovian model such as the one we consider here. By computing the spectral gap of the transition matrix of the FMM, we explore the relationship between the equilibration time and the average reservoir exit time for a small network (Fig. 2b, inset) in both the absence and presence of crowding. In the absence of crowding, networks with lower average reservoir mean exit times will facilitate quicker equilibration (Fig. 2b, dot-dashed curve). Intuitively this is unsurprising as individuals attempt to move between reservoirs more frequently. With crowding effects incorporated, the monotonicity between the average reservoir mean exit time and the equilibration time is lost (Fig. 2b, solid curve). The equilibration time rises once the volume-excluding interactions within the narrow channels induce a bottle-neck that impedes transport between reservoirs. Thus, a combination of the localised geometry responsible for creating narrow channels (geometry-induced crowding) and interactions between the individuals within a narrow channel (crowding between individuals) can significantly increase the time taken for a population to equilibrate. We derive an analytical condition for when the equilibrium occupancy of each narrow channel lattice site is high and thus crowding effects are important, which is $\langle {{{{{{{\boldsymbol{\tau }}}}}}}}\rangle \ll {N}_{{{{{\rm{HD}}}}}}/\left(\alpha | {{{{{{{\mathcal{V}}}}}}}}| \right)$, where ${N}_{{{{{\rm{HD}}}}}}=\left(N-{K}_{{{{{\rm{tot}}}}}}\right)$ is the effective number of particles in the reservoirs and K_tot is the total number of lattice sites across all narrow channels (see Methods, section “High-density condition”). We will term this regime the high-density regime and it determines when the combination of localised geometry and crowding is most prominent (Fig. 2b, left shaded region).

Whilst the FMM is a conceptually ideal way to describe crowded transport in complex geometries, evaluating the equilibration time is computationally infeasible for all but the simplest networks (Fig. 2b, inset) as the dimensionality of the transition matrix for the FMM is ${{{{{{{\mathcal{O}}}}}}}}\left({2}^{{K}_{{{{{\rm{tot}}}}}}}{N}^{| {{{{{{{\mathcal{V}}}}}}}}| -1}\right)$ (see Supplementary Note 1). Therefore, to further investigate the role of crowding and geometry on transport behaviour it is critical to consider dimensionality reduction techniques.

Scaling to large geometries

Networked representations of complex environments (Fig. 1a) may contain on the order of hundreds or even thousands of interconnected reservoirs. In light of such, we require models that scale computationally to large environments whilst incorporating details of their microscopic spatial structure. The high dimensionality of the FMM arises from explicitly modelling the occupancy of every lattice site along every narrow channel.

To make progress we introduce a reduced Markov model (RMM) which, in lieu of considering the dynamics within the narrow channels in detail, allows for direct exchange of individuals between reservoirs (Fig. 2d). This approach is reminiscent of the average current calculations for exclusion processes between two open boundaries⁵². For the RMM let n be the configuration vector, where n_i is the number of individuals in the ith reservoir. Focussing on the high-density regime (Supplementary Note 1 discusses the low-density regime), where crowding effects are most important, the rate at which exchange between two connected reservoirs i and j occurs, denoted ${k}_{i,j}^{{{{{\rm{HD}}}}}\,}({{{{{{{\boldsymbol{n}}}}}}}})$, is calculated by considering the dynamics of the interacting individuals along the narrow channels (see the “Methods”, section “Reduced Markov model”). By invoking particle–hole duality⁵³, it is convenient to consider the dynamics of the vacant sites rather than the individuals explicitly. The resulting expression for ${k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}({{{{{{{\boldsymbol{n}}}}}}}})$ is given by

$${k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}({{{{{{{\boldsymbol{n}}}}}}}})=\frac{1}{{K}_{(i,j)}-1}{\left(\frac{{\tau }_{j}^{-1}({n}_{j}+1)+2\alpha }{{\alpha }^{2}}+\frac{{K}_{(i,j)}-2}{2\alpha }\right)}^{-1}.$$

(1)

Similar to the FMM, the RMM is a CTMC and the reciprocal of the spectral gap of the transition matrix provides the equilibration time. However, the dimensionality of the RMM is still prohibitively high, ${{{{{{{\mathcal{O}}}}}}}}\left({N}^{| {{{{{{{\mathcal{V}}}}}}}}| -1}\right)$, and does not scale computationally to large complex environments.

Further dimensionality reduction can be achieved through a continuous mean-field approximation of reservoir occupancy in the RMM. Introducing x, such that x_i = n_i/N_HD is the fraction of the population that lies within the ith reservoir, and expanding the chemical master equations governing the RMM as a Taylor series provides the corresponding Fokker–Planck equation, a partial differential equation describing the evolution of the probability density for the distribution of individuals (see the “Methods”, section “Ornstein–Uhlenbeck process”). In equilibrium, the networked distribution of the population is determined by the reservoir geometry and is given by x* such that ${x}_{i}^{* }={\tau }_{i}/\mathop{\sum }\nolimits_{j = 1}^{| {{{{{{{\mathcal{V}}}}}}}}| }{\tau }_{j}$ (see the “Methods”, section “Ornstein–Uhlenbeck process”). Localising the Fokker–Planck equation about x* reveals that the population dynamics as the networked distribution equilibrates is governed by an Ornstein–Uhlenbeck (OU) process which is known to be Gaussian⁵⁴. Thus, from an initial configuration of individuals x₀, the configuration at time t follows a multivariate normal distribution with known mean vector μ(t; x₀) given by

$${{{{{{{\boldsymbol{\mu }}}}}}}}(t;{{{{{{{{\boldsymbol{x}}}}}}}}}_{0})=\exp \left(-t{{{{{{{{\bf{F}}}}}}}}}^{{{{{\rm{HD}}}}}}\right){{{{{{{{\boldsymbol{x}}}}}}}}}_{0}+\left({{{{{{{\bf{I}}}}}}}}-\exp \left(-t{{{{{{{{\bf{F}}}}}}}}}^{{{{{\rm{HD}}}}}}\right)\right){{{{{{{{\boldsymbol{x}}}}}}}}}^{* },$$

(2)

where I is the identity matrix, and covariance matrix Σ(t; x₀) given by

$${{{{{{{\mathbf{\Sigma }}}}}}}}(t;{{{{{{{{\boldsymbol{x}}}}}}}}}_{0})=\int\nolimits_{0}^{t}\exp \left(-u{{{{{{{{\bf{F}}}}}}}}}^{{{{{\rm{HD}}}}}}\right){{{{{{{{\bf{D}}}}}}}}}^{{{{{\rm{HD}}}}}}\exp \left(-u{\left({{{{{{{{\bf{F}}}}}}}}}^{{{{{\rm{HD}}}}}}\right)}^{T}\right){{{{{{{\rm{d}}}}}}}}u,$$

(3)

where F^HD and D^HD are drift and diffusion matrices, respectively (see the “Methods”, section “Ornstein–Uhlenbeck process”). The entries of the drift matrix F^HD are given by

$${F}_{i,j}^{\,{{{{\rm{HD}}}}}\,}={{{{{{{{\mathcal{A}}}}}}}}}_{i,j}\frac{{\left({k}_{i,j}^{{{{{\rm{HD}}}}}}\right)}^{\prime}({N}_{{{{{\rm{HD}}}}}}{{{{{{{{\bf{x}}}}}}}}}^{* })}{{N}_{{{{{\rm{HD}}}}}}},$$

(4)

for i ≠ j, and ${F}_{i,i}^{\,{{{{\rm{HD}}}}}}=-{\sum }_{j\ne i}{F}_{j,i}^{{{{{\rm{HD}}}}}\,}$ for $1\le i\le | {{{{{{{\mathcal{V}}}}}}}}|$, where ${{{{{{{{\mathcal{A}}}}}}}}}_{i,j}$ are the entries of the network adjacency matrix and ${k}_{i,j}^{\,{{{{\rm{HD}}}}}}({N}_{{{{{\rm{HD}}}}}}{{{{{{{{\bf{x}}}}}}}}}^{* })$ is the continuous extension of ${k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}({{{{{{{\boldsymbol{n}}}}}}}})$ defined in Eq. (1). The entries of the diffusion matrix D^HD are

$${D}_{i,j}^{\,{{{{\rm{HD}}}}}\,}=-{{{{{{{{\mathcal{A}}}}}}}}}_{i,j}\frac{\left({k}_{i,j}^{\,{{{{\rm{HD}}}}}}({N}_{{{{{\rm{HD}}}}}}{{{{{{{{\bf{x}}}}}}}}}^{* })+{k}_{j,i}^{\,{{{{\rm{HD}}}}}}({N}_{{{{{\rm{HD}}}}}}{{{{{{{{\bf{x}}}}}}}}}^{* })\right)}{2{N}_{\,{{{{\rm{HD}}}}}\,}^{2}},$$

(5)

for i ≠ j, and ${D}_{i,i}^{\,{{{{\rm{HD}}}}}}=-{\sum }_{j\ne i}{D}_{i,j}^{{{{{\rm{HD}}}}}\,}$ for $1\le i\le | {{{{{{{\mathcal{V}}}}}}}}|$. Equation (2) reveals that the equilibration time of the OU process is dictated by the spectral gap of the drift matrix F^HD which is in the form of a networked graph Laplacian. The spectral gap of F^HD accurately predicts the equilibration time for the FMM (Fig. 2b) and is inexpensive to compute. In particular, the transition matrix for the FMM in Fig. 2b has a dimension of 6968 whilst the weighted graph Laplacian F^HD has a dimension of three. We now exploit this remarkable dimensionality reduction to reveal the fundamental principles that govern topological optimisation of equilibration times in crowded environments.

Equilibration times are highly sensitive to an environments network topology

To demonstrate how network topology can affect equilibration times we first consider a toy network consisting of five reservoirs (Fig. 3a, inset). The three-dimensional reservoir positions x_i are uniformly sampled within a unit sphere. The integer narrow channel lengths between reservoirs i and j are given by K_(i,j) = ⌈∣∣x_i − x_j∣∣/Δ⌉, where Δ = 10⁻³ is the width of the narrow channels and ∣∣x_i − x_j∣∣ is the Euclidean distance between reservoirs i and j. We now consider all 728 possible connected networks with five reservoirs and their corresponding equilibration times.

Fig. 3: Optimal topologies that minimise networked equilibration times.

a Equilibration time and total edge length for all 728 connected topologies for a configuration of five reservoirs (inset). The reservoir colours represent the change in elevation highlighting how they are positioned in three-dimensional space. The optimal frontier is highlighted in asterisks and given labels (i)–(xiv). For a given restriction (vertical line) the optimal network is given by label (viii) and the asterisk is red. b Topologies of the networks that lie on the optimal frontier in panel (a). c Averaged coordinates from numerically estimated optimal frontiers (Supplementary Note 4) with increasing levels of reservoir heterogeneity. The vectors of reservoir mean exit times are t(0), t(0.5) and t(1) (inset). The shaded regions represent the standard deviation either side of the mean. d The range of equilibration factors of both optimal and non-optimal networks for homogeneous, t(0), and heterogeneous, t(1), reservoir geometries. The shaded regions outlines the boundary of a point cloud from 5000 different configurations of 10 reservoirs (Supplementary Note 4), both optimal and non-optimal. e The range of equilibration factors of both optimal and non-optimal networks for heterogeneous, t(1), reservoir geometries. The shaded regions outlines the boundary of a point cloud from 5000 different configurations of 10 reservoirs (Supplementary Note 4), both optimal and non-optimal. f The bar charts (i)–(x) show the weighted degree distribution for both optimal and non-optimal networks across the range of rescaled total edge lengths. The heterogeneous vector of reservoir mean exit times used in (c) and (f) is ${{{{{{{\boldsymbol{\tau }}}}}}}}=\left({2}^{1},{2}^{2},\ldots ,{2}^{10}\right)$. All data presented in (c)–(f) uses the same 5000 configurations of 10 reservoirs with randomly generated ensembles of narrow channel lengths ${{{{{{{\mathcal{K}}}}}}}}$ (Supplementary Note 4).

As a function of topology, equilibration times, calculated from the spectral gap of F^HD, vary over several orders of magnitude (Fig. 3a). The topology that induces the quickest equilibration is the complete network (Fig. 3a, b-(xiv)), because the opportunities for individuals to exchange between connected reservoirs are maximised when every connection is present. However, a complete network is inappropriate to describe most complex environments due to spatial constraints limiting the connectivity of the reservoirs (Fig. 1a–d). The connectivity of a network can be quantified by its total edge length, the sum of the narrow channel lengths present in the network. Imposing a restriction on the total edge length (Fig. 3a, vertical line) reveals a new non-complete optimal network (Fig. 3a, b-(viii)). By varying the restriction over the range of total edge lengths, as defined by the minimum spanning tree(s) and the complete network (Fig. 3a, b-(i) and (xiv), respectively), a frontier of optimal networks arises (Fig. 3a, b). Networks that lie on the optimal frontier, which we term the optimal networks, represent environments in which a population equilibrates efficiently, under a given restriction on the environmental connectivity.

A global envelope of optimal networks

To explore properties of the optimal frontier (Fig. 3a) we temporarily assume homogeneous reservoir exit times, an assumption that models environments with regular periodic structure such as synthetic porous nanomaterials⁵⁵. Thus, networks that lie on the optimal frontier depend solely on the ensemble ${{{{{{{\mathcal{K}}}}}}}}$ of all possible narrow channel lengths which, in turn, depends upon the spatial configuration of the reservoirs (Supplementary Note 4). Comparing optimal frontiers between distinct ensembles ${{{{{{{\mathcal{K}}}}}}}}$ requires two rescalings (Supplementary Note 2). Firstly, the total edge length of a network must lie in an interval defined by the total edge lengths of the minimum spanning tree and the complete network. The rescaled total edge length linearly maps this interval to lie between zero and one and provides a dimensionless measure of connectedness. Such a rescaling ensures that the rescaled total edge length contains information about the distribution of all possible edge lengths not just the edge lengths present in the current network. Secondly, the equilibration times are normalised by the minimum equilibration time, which belongs to the complete network, and thus yields values greater than or equal to one which represent how many factors slower equilibration occurs for a given network compared to the complete network.

Numerical evidence strongly supports the hypothesis that the rescaled optimal frontier follows a global curve that is independent of ${{{{{{{\mathcal{K}}}}}}}}$ and hence is independent of the spatial configuration of the reservoirs (Supplementary Fig. 6). Over many distinct ensembles ${{{{{{{\mathcal{K}}}}}}}}$, the variation in the optimal frontier becomes vanishingly small as the number of reservoirs increases (Supplementary Fig. 6b–d). The global curve persists even for an ensemble of channel lengths that are intentionally sampled from an extremely heterogeneous distribution to ensure that the curve is not a feature of our sampling procedure (Supplementary Fig. 6e). The apparent persistence of the globally optimal frontier has significant implications for optimal network design; testing the optimality of a proposed network merely requires direct comparison of the rescaled total edge length and equilibration factor (two cheap-to-compute network statistics) to the global curve. Moreover, the global curve provides a benchmark to compare the efficacy of algorithms designed to efficiently construct optimal or close to optimal networks (Supplementary Note 4).

Reservoir heterogeneity leads to minimised equilibration times in cases of restricted connectivity

Complex geometries can exhibit a range of microscopic spatial structures (Fig. 1b), and this gives rise to reservoir heterogeneity within the corresponding networks (Fig. 1c). The effects of such heterogeneities can be encapsulated by a vector of distinct reservoir exit times τ. To meaningfully compare the optimal frontiers that arise from two different vectors of reservoir exit times we require that both vectors have the same ensemble average 〈τ〉. Such a requirement guarantees that the narrow channel equilibrium occupancy is held constant (see the “Methods”, section “Equilibrium occupancy”), and thus changes in optimal equilibration times occur solely due to reservoir heterogeneity rather than a change in crowding effects. We note that the narrow channel equilibrium occupancy can be viewed as the probability that an attempted jump to a lattice site within a narrow channel is aborted, and thus quantifies the strength of the crowding effects. To systematically explore how heterogeneity impacts the optimal frontier we introduce a vector of reservoir exit times ${{{{{{{\boldsymbol{t}}}}}}}}\left(\phi \right)$ with ith entry ${t}_{i}\left(\phi \right)=\left(1-\phi \right)\langle {{{{{{{\boldsymbol{\tau }}}}}}}}\rangle +\phi {\tau }_{i}$ for ϕ ∈ [0, 1]. The new reservoir exit times ${{{{{{{\boldsymbol{t}}}}}}}}\left(\phi \right)$ depend upon a heterogeneous yet arbitrary vector of mean exit times τ, and the parameter ϕ controls the extent of reservoir heterogeneity, where ${{{{{{{\boldsymbol{t}}}}}}}}(0)=\left(\langle {{{{{{{\boldsymbol{\tau }}}}}}}}\rangle ,\ldots ,\langle {{{{{{{\boldsymbol{\tau }}}}}}}}\rangle \right)$ represents homogeneous reservoirs, ensuring $\langle {{{{{{{\boldsymbol{t}}}}}}}}\left(\phi \right)\rangle =\langle {{{{{{{\boldsymbol{\tau }}}}}}}}\rangle$ for all values of ϕ. For increasing levels of reservoir heterogeneity, which is achieved by increasing ϕ (Fig. 3c, inset), the shape of the optimal frontier changes significantly, and optimal networks achieve globally minimised equilibration times (close to the equilibration time of the complete network) with significantly reduced connectivity (Fig. 3c). Thus, heterogeneity within the internal structure of complex environments has the potential to facilitate globally efficient equilibration in environments with spatially restricted connectivity.

Optimal networks have distinct topological structure

The topological structure of optimal networks can be characterised via a weighted degree distribution that arises from considering the diagonal entries of the weighted graph Laplacian, F^HD. For the complete network the ith diagonal entry of F^HD is proportional to ${R}_{i}={\sum }_{j\ne i}{\left({\tau }_{j}{K}_{(i,j)}\right)}^{-1}$ which represents the total transition rate out of the ith reservoir when viewing the weighted graph Laplacian as a rate matrix (see Supplementary Note 2). As every connection between reservoirs is present in the complete network we term R_i the potential transition rate of reservoir i and we order the reservoirs such that ${R}_{1} < \cdots < {R}_{| {{{{{{{\mathcal{V}}}}}}}}| }$. The ratio of the ith diagonal entry of F^HD for a network ${{{{{{{\mathcal{G}}}}}}}}$ with adjacency matrix ${{{{{{{\mathcal{A}}}}}}}}$ and the ith diagonal entry of F^HD for the complete network is ${W}_{i}\left({{{{{{{\mathcal{G}}}}}}}};{{{{{{{\mathcal{K}}}}}}}},{{{{{{{\boldsymbol{\tau }}}}}}}}\right)={\sum }_{j\ne i}{{{{{{{{\mathcal{A}}}}}}}}}_{i,j}{\left({\tau }_{j}{K}_{(i,j)}\right)}^{-1}/{R}_{i}$ and represents the fraction of the potential transition rate of reservoir i present in the network ${{{{{{{\mathcal{G}}}}}}}}$. The weighted degree distribution is defined by ${w}_{i}\left({{{{{{{\mathcal{G}}}}}}}};{{{{{{{\mathcal{K}}}}}}}},{{{{{{{\boldsymbol{\tau }}}}}}}}\right)={W}_{i}\left({{{{{{{\mathcal{G}}}}}}}};{{{{{{{\mathcal{K}}}}}}}},{{{{{{{\boldsymbol{\tau }}}}}}}}\right)-\mathop{\sum }\nolimits_{j = 1}^{| {{{{{{{\mathcal{V}}}}}}}}| }{W}_{j}\left({{{{{{{\mathcal{G}}}}}}}};{{{{{{{\mathcal{K}}}}}}}},{{{{{{{\boldsymbol{\tau }}}}}}}}\right)/| {{{{{{{\mathcal{V}}}}}}}}|$ for $1\le i\le | {{{{{{{\mathcal{V}}}}}}}}|$. The weights ${w}_{i}\left({{{{{{{\mathcal{G}}}}}}}};{{{{{{{\mathcal{K}}}}}}}},{{{{{{{\boldsymbol{\tau }}}}}}}}\right)$ are translated such that if ${w}_{i}\left({{{{{{{\mathcal{G}}}}}}}};{{{{{{{\mathcal{K}}}}}}}},{{{{{{{\boldsymbol{\tau }}}}}}}}\right) \; > \;0$ then the ith reservoir has a ratio ${W}_{i}\left({{{{{{{\mathcal{G}}}}}}}};{{{{{{{\mathcal{K}}}}}}}},{{{{{{{\boldsymbol{\tau }}}}}}}}\right)$ greater than the network average, and is referred to as being over-represented in the network. Similarly, a reservoir with ${w}_{i}\left({{{{{{{\mathcal{G}}}}}}}};{{{{{{{\mathcal{K}}}}}}}},{{{{{{{\boldsymbol{\tau }}}}}}}}\right) \; < \; 0$ is said to be under-represented. Naively, one might expect reservoirs with the highest potential transition rates to be over-represented in any network that lies on an optimal frontier, as connections between reservoirs with high transition rates should encourage faster equilibration. However, we discover that the structure of optimal networks varies greatly depending on the restriction on the rescaled total edge length.

The structure of networks that lie on the optimal frontier compared with non-optimal networks (randomly sampled connected topologies) is distinct across all rescaled total edge lengths (Fig. 3d, e), with the greatest contrast seen for networks with mid-range connectivity (Fig. 3d–f(iii)–(viii)). Moreover, the weighted degree distribution highlights how reservoirs can be connected to achieve optimality. Optimal networks with low connectivity and reservoir homogeneity prefer connections between reservoirs with high potential transition rates (Fig. 3f(i) orange/green), on the other hand, for highly connected optimal networks the relative importance of the reservoirs is reversed (Fig. 3f(x) orange/green). Interestingly, as connectivity varies between the two extremes, optimal networks involve over-representation of reservoirs with both high and low potential transition rates (Fig. 3f(vi)–(viii) orange/green). This transitional behaviour vanishes if reservoir heterogeneity is sufficiently high, where reservoirs with high potential transition rates are over-represented for all levels of connectivity (Fig. 3f blue/purple). Even for highly connected networks, the absence of a single important connection between reservoirs can significantly increase equilibration times by over a factor of four in heterogeneous environments (Supplementary Note 2 and Supplementary Fig. 8). Collectively our results demonstrate the ability of the weighted degree distribution, as well as the graph Laplacian F^HD, to reveal connections between geometric structure and optimal transport that could not have been identified with traditional modelling approaches.

The dynamics of tagged individuals are highly sensitive to narrow channel length

The detailed dynamics of a tagged individual within a population is of interest across a broad range of disciplines^7,56. For example, the differentiated fate of a stem cell can hinge upon the spatial and temporal dynamics of a single protein within the crowded intracellular environment⁵⁷. A significant benefit of our framework is that it readily extends to provide information at the level of a single tagged individual. The microscopic dynamics of a tagged individual are identical to the dynamics of any individual within the FMM. Therefore, the transition of a tagged individual between adjacent reservoirs i and j via a connecting narrow channel of length K_(i,j) occurs as follows. First a tagged individual in reservoir i will jump into the first lattice site adjacent to reservoir i on the narrow channel connecting the ith and jth reservoirs. In the high-density regime, the tagged particle will jump back into reservoir i at rate α or jump into the adjacent (second) lattice site when a background individual is exchanged from the ith to the jth reservoirs. The latter jump occurs at a significantly lower rate ${k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({{{{{{{\boldsymbol{n}}}}}}}}\right)$ (Eq. (1)) and almost always the tagged individual returns to the ith reservoir. For this reason we consider a tagged individual to have ‘properly’ entered the narrow channel only when it reaches the second lattice site (Fig. 4a(i), (ii)). Then, as background individuals continue to be exchanged between reservoirs i and j, the tagged individual undergoes a random walk along the sites of the narrow channel until either being absorbed back into the ith reservoir (Fig. 4a(i)), or absorbed into the jth reservoir (Fig. 4a(iii)). The latter occurs with probability ${p}_{{{{{\rm{TI}}}}}}\left({x}_{i},{x}_{j};{K}_{(i,j)}\right)$, where the fractions of the population that occupy the ith and jth reservoirs at the moment when the tagged individual first enters the narrow channel (Fig. 4a(ii)) are denoted x_i and x_j, respectively. The probability ${p}_{{{{{\rm{TI}}}}}}\left({x}_{i},{x}_{j};{K}_{(i,j)}\right)$ is given by

$${p}_{{{{{\rm{TI}}}}}}\left({x}_{i},{x}_{j};{K}_{(i,j)}\right) \sim {f}_{0}\left({x}_{i},{x}_{j}\right){\left[\mathop{\sum }\limits_{k = 0}^{{K}_{(i,j)}-2}{f}_{k}\left({x}_{i},{x}_{j}\right)\right]}^{-1},$$

(6)

where the functions ${f}_{k}\left({x}_{i},{x}_{j}\right)$ are given by

$${f}_{k}\left({x}_{i},{x}_{j}\right)= {\left(\frac{{\tau }_{i}}{{\tau }_{j}}\right)}^{k}{\left(\frac{{x}_{i}}{{x}_{i}+{x}_{j}}+\frac{2-k}{{N}_{{{{{\rm{HD}}}}}}\left({x}_{i}+{x}_{j}\right)}\right)}^{{N}_{{{{{\rm{HD}}}}}}{x}_{i}+3/2-k}\\ \times{\left(\frac{{x}_{j}}{{x}_{i}+{x}_{j}}+\frac{1+k}{{N}_{{{{{\rm{HD}}}}}}\left({x}_{i}+{x}_{j}\right)}\right)}^{{N}_{{{{{\rm{HD}}}}}}{x}_{j}+1/2+k}.$$

(7)

The probability p_TI is referred to as the tagged individual crossing probability (see the “Methods”, section “Tagged individual crossing probability” for a derivation).

The successful crossing of a tagged individual that has just entered the narrow channel (Fig. 4a(ii)) requires a net exchange of several background individuals from the ith to the jth reservoir. The probability, p_TI, that this net exchange occurs depends on ${x}_{i}/\left({x}_{i}+{x}_{j}\right)$, the fractional occupancy of the ith reservoir relative to the jth (Fig. 4b). For fractional occupancies greater than the equilibrium fractional occupancy, which is ${x}_{i}^{* }/\left({x}_{i}^{* }+{x}_{j}^{* }\right)$ where ${x}_{i}^{* }={\tau }_{i}/\mathop{\sum }\nolimits_{j = 1}^{| {{{{{{{\mathcal{V}}}}}}}}| }{\tau }_{j}$ (Fig. 4b, vertical dashed line), as the population equilibrates there is a bias favouring exchange of background individuals from the ith to the jth reservoir which subsequently increases the tagged individual crossing probability. However, the probability p_TI becomes incredibly sensitive to the fractional occupancy as the length of the narrow channel increases (Fig. 4b, arrow). Indeed, a successful crossing of a tagged individual can require that the fractional occupancy of the ith reservoir is significantly above the equilibrium occupancy (Fig. 4b, red curve). Thus, in an equilibrated population, the probability that a tagged individual traverses between two adjacent reservoirs is effectively zero if the narrow channel is too long. In particular, for homogeneous reservoirs (τ_i = τ) we find that the tagged individual crossing probability is effectively zero when ${K}_{(i,j)}\ge \sqrt{N/| {{{{{{{\mathcal{V}}}}}}}}| }$ (Supplementary Note 1 and Supplementary Fig. 5).

Fig. 4: Narrow channel lengths affect tagged individual dynamics.

a Diagrammatic representation of how a tagged individual (orange) transitions from one reservoir (large circles) to another, and the net exchange of background individuals (black) required to do so. (i) The tagged individual is initially in the left-most reservoir. (ii) The tagged individual is considered to have entered the narrow channel only when it reaches the second lattice site denoted by the 2. (iii) The tagged individual has reached the right-most reservoir. b The tagged individual crossing probability p_TI (Eq. (6)) for increasing narrow channel lengths K_(i,j) ∈ {4, 25, 400, 650}. The blue and red lines correspond to channel lengths of 4 and 650, respectively. c The tagged individual mean exit time m_TI (Eq. (8)) for increasing narrow channel lengths K_(i,j) ∈ {5, 10, 25, 50, 100, 150} where the curve corresponding to K_(i,j) = 150 is highlighted in green. The parameters used in (b) and (c) are as follows. The two reservoir exit times τ_i and τ_j are given by τ_i = τ_j = 0.1 and the number of individuals is given by N = 10³.

The temporal dynamics of tagged individuals are drastically affected by narrow channel length. For an individual that has just entered the second lattice site along the narrow channel (Fig. 4a(ii)), the tagged individual mean exit time, ${m}_{{{{{\rm{TI}}}}}}\left({x}_{i},{x}_{j};{K}_{(i,j)}\right)$, denotes the mean time taken for the tagged individual to exit the channel at either end, and is given by

$${m}_{{{{{\rm{TI}}}}}}\left({x}_{i},{x}_{j};{K}_{(i,j)}\right) \sim {p}_{{{{{\rm{TI}}}}}}\left({x}_{i},{x}_{j};{K}_{(i,j)}\right)\left[{h}_{1}\left({x}_{j}\right)+\mathop{\sum }\limits_{k=2}^{{K}_{(i,j)}-2}\mathop{\sum }\limits_{\ell =1}^{k}\frac{{h}_{\ell }({x}_{j}){f}_{k}\left({x}_{i},{x}_{j}\right)}{{f}_{\ell }\left({x}_{i},{x}_{j}\right)}\right],$$

(8)

where ${h}_{\ell }({x}_{j})=\left({K}_{(i,j)}-1\right)\left({N}_{{{{{\rm{HD}}}}}}{x}_{j}+\ell \right)/\left({\tau }_{j}{\alpha }^{2}\right)$, and the ${f}_{k}\left({x}_{i},{x}_{j}\right)$ are as in Eq. (7) (see the “Methods”, section “Tagged individual mean exit time” for a derivation). The effect of increasing the length of the narrow channel K_(i,j) on m_TI is two-fold. Firstly, the tagged individual mean exit time increases drastically (Fig. 4c, arrow). Secondly, as for p_TI, m_TI becomes incredibly sensitive to the fractional occupancy of the two reservoirs. Fractional occupancies of the ith reservoir slightly above equilibrium introduce a temporary bias that encourages the tagged individual to move further along the channel. Once the background individuals have equilibrated the bias is removed whilst the tagged individual remains within the internal lattice sites of a long narrow channel. Relying solely on the unbiased stochastic fluctuations of background individuals increases the time taken for the tagged individual to exit the channel by many orders of magnitude (Fig. 4c, peak of green curve), in particular this time can significantly exceed the equilibration time of the entire population (Supplementary Fig. 3b).

Crowding alters the paths taken by tagged individuals

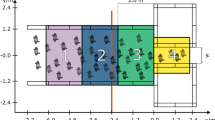
Exploration of the motion of tagged individuals throughout a complex and crowded environment requires highly scalable networked transport models capable of extracting information at the level of the individual. We extend our framework, using the concepts of the tagged individual crossing probability, p_TI, and mean exit time, m_TI, to provide such models of individual dynamics within both fixed and stochastically fluctuating background populations (Supplementary Note 1). For a fixed equilibrated population, the spatial dynamics of a tagged individual can be investigated via a discrete networked random walk model. The dynamics of this random walk model are revealed via analysis of the transition matrix, rather than via stochastic simulation (Supplementary Note 4). As such, many useful statistics describing the dynamics of tagged individuals within complex and crowded environments are immediately available. To highlight the utility of the discrete random walk model we consider a first-passage process⁵⁸, reminiscent of the Notch signalling pathway where an intracellular protein traverses between the cellular and nuclear membranes⁵⁷. We adopt a caricature representation of the intracellular geometry in the form of a random geometric network (Fig. 5a, b and Supplementary Note 4), and consider the first-passage properties of a tagged individual initially within a reservoir adjacent to the cellular membrane (Fig. 5a, b, outer circle) whose position evolves according to the networked discrete random walk (Supplementary Note 4) before terminating at a reservoir adjacent to the nucleus (Fig. 5a, b, inner circle).

Fig. 5: The paths of tagged individuals between the cellular and nuclear membranes are heavily altered due to crowding.

a and b Expected number of crossings of each narrow channel with and without crowding in a realisation of a cellular signalling network with 1000 reservoirs (Supplementary Note 4). c The normalised frequency of the number of channels for a given expected number of crossings. d Expected path length of a tagged individual as a function of the position of the initial entry at the cellular membrane. The inset describes the position of the nucleus (small circle) and the cell membrane (larger circle). The extremal entry points on the membrane are shown by the two stars. The magenta star is the distal entry point, and the cyan star is the proximal entry point. All data presented in (c) and (d) is averaged over 100 realisations of a random geometric network (Supplementary Note 4). Parameters for the discrete random walks (Supplementary Note 1) used in (a)–(d) are as follows. The number of individuals is given by N = 3 × 10⁴, α = 1, and the reservoir exit times are given by τ_i = 0.1 for every reservoir i.

By comparing our discrete random walk model to an almost identical model that does not consider crowding effects (Supplementary Note 4), we discover that crowding effects within the narrow channels drastically alters the paths taken by tagged individuals (Fig. 5). The expected number of times an individual traverses a narrow channel becomes highly sensitive to local network topology when crowding effects are incorporated (Fig. 5a, b). The negligible chance that a crowded tagged individual traverses a long narrow channel (Fig. 4b and Supplementary Fig. 6) significantly widens the distribution of the expected number of crossings (Fig. 5c and a, b highlighted regions), and tagged individuals follow paths that visit reservoirs connected via short narrow channels significantly more often than longer channels (Supplementary Fig. 4). Favouring shorter narrow channels subsequently favours indirect paths (Supplementary Fig. 4a) resulting in an increase in the total path length of an individual that moves from the cellular to the nuclear membrane (Fig. 5d). The alterations of the dynamics of tagged individuals due to crowding, as detailed above, has important implications for the efficiency of signalling pathways and subsequent downstream processes⁵⁹.

Discussion

Our results highlight how networks provide an effective framework through which to reveal and quantify the combined influences of geometry and crowding on the transport properties of individuals confined within finite complex environments. Moreover, detailed network analysis uncovered global relationships between population-level transport behaviour and optimal networked topologies, as well as the salient network features responsible for optimisation. Our framework provides insights into the interplay between geometry, crowding and transport, with such insights being of relevance for a range of geometrically regulated transport processes.

The work presented in this paper focusses on modelling the temporal fluctuations of particles within the reservoirs of a network. This was achieved through averaging the effects of crowding within narrow channels by assuming that the narrow channel occupancy is held constant. However, previous work has shown that crowding effects can give rise to strongly fluctuating densities within narrow channels⁵². As such, it would be interesting to extend our framework to allow for both the occupancy of reservoirs and narrow channels to fluctuate and explore whether our conclusions about optimal networked topologies change. This would offer a means to test whether the global envelope of optimal networks persists, providing further evidence of a possible universal relationship between rescaled total edge length and optimal equilibration.

Beyond identifying global connections between crowding, geometry and transport, our framework provides an efficient computational tool to perform more focussed investigations. For example, cardiomyocyte cells have an intracellular environment consisting of mitochondrial and myofibril filaments. Patients suffering from diabetic cardiomyopathy have been shown to have highly clustered and disordered mitochondrial distributions^60,61. It has been hypothesised that these alterations to the intracellular geometry help regulate the transport of essential metabolites and increase the overall energy supply to the cell in an effort to maintain regular heart function⁶⁰. A networked modelling approach might offer insights into the functional role of the observed intracellular restructuring. Analysing the structure of networks extracted from light-sheet microscopy images (Supplementary Fig. 10) would quantify the structural differences between healthy and diabetic cardiomyocytes and studying the transport of metabolites on these networks would provide a means to test whether these changes in intracellular geometry can improve cellular bioenergetics. Moreover, the computational efficiency of our framework increases the number of experimental images that can be studied compared with traditional approaches that are constrained by using high-resolution meshes. Studying a large number of distinct cellular geometries will be critical to developing a deeper understanding of how intracellular restructuring may regulate cellular bioenergetics.

Our framework offers opportunities for generalisation. The RMM is formulated as a chemical reaction network⁶² and thus can immediately support reactions between individuals, where subsequent coarse-graining will result in a Fokker–Planck equation capable of investigating geometry-controlled kinetics⁶³. Included within Supplementary Note 3 is a generalisation of our framework that supports active transport. We study a partially asymmetric simple exclusion process (PASEP) that allows individuals to undergo bi-directional motion along narrow channels but with a bias in one direction. Extending to active transport opens the door to investigating the geometric influences on highly crowded transport phenomena across a wide array of spatial scales, from mRNA translocation along intracellular microtubule networks⁶⁴, to molecular trafficking between cells connected via cytonemes⁶⁵ or plasmodesmata⁶⁶, to the transport of sediment subjected to flows within porous media⁶⁷.

By reconceptualising how we model crowded, geometrically constrained transport, we can also gain insights within fields such as optimal synthetic design⁶⁸ and molecular cell biology⁶⁹, to name a few. This work presents a versatile framework that paves the way for furthering our understanding of the fundamental connections between crowding, networked geometry and transport beyond traditional modelling paradigms.

Methods

Full Markov model

In this section, we formally introduce the FMM as a continuous time random walk. Consider a network ${{{{{{{\mathcal{G}}}}}}}}=\{{{{{{{{\mathcal{V}}}}}}}},{{{{{{{\mathcal{E}}}}}}}}\}$, where ${{{{{{{\mathcal{V}}}}}}}}$ is the set of reservoirs (nodes) and ${{{{{{{\mathcal{E}}}}}}}}$ the set of narrow channels (edges) that connect the reservoirs. Assigning indices e to each narrow channel arbitrarily, the narrow channels have non-dimensional length ${K}_{e}\in {{\mathbb{Z}}}_{\ge 1}$ for $1\le e\le | {{{{{{{\mathcal{E}}}}}}}}|$, which denotes the number of lattice sites in the narrow channel (in the “Results” section we use the notation K_(i,j) to denote the number of lattice sites in the narrow channel connecting the ith and jth reservoirs, to ensure clarity we will switch between the notations K_(i,j) and K_e as appropriate). Each narrow channel is assigned an arbitrary polarity and the lattice sites have indices {1, …, K_e}. A total of N individuals populate the network and their configuration at time t is described by the state vector S(t). The state vector is written as a concatenation of additional vectors, ${{{{{{{\bf{S}}}}}}}}(t)=({{{{{{{\bf{R}}}}}}}}(t),{{{{{{{{\bf{N}}}}}}}}}_{1}(t),\ldots ,{{{{{{{{\bf{N}}}}}}}}}_{| {{{{{{{\mathcal{E}}}}}}}}| }(t))$, where, for $1\le i\le | {{{{{{{\mathcal{V}}}}}}}}|$, [R(t)]_i = R_i(t) is the number of individuals in reservoir i at time t. For $1\le e\le | {{{{{{{\mathcal{E}}}}}}}}|$ and 1 ≤ k ≤ K_e, ${[{{{{{{{{\bf{N}}}}}}}}}_{e}(t)]}_{k}={N}_{e,k}(t)$ is the occupancy of the kth lattice site along the eth narrow channel. Let ${{{\Omega }}}_{N,{{{{{{{\mathcal{G}}}}}}}}}$ be the set of legal configurations for a population of N individuals on the network ${{{{{{{\mathcal{G}}}}}}}}$. The set ${{{\Omega }}}_{N,{{{{{{{\mathcal{G}}}}}}}}}$ consists of vectors ${{{{{{{\bf{s}}}}}}}}=({{{{{{{\bf{r}}}}}}}},{{{{{{{{\bf{n}}}}}}}}}_{1},\ldots ,{{{{{{{{\bf{n}}}}}}}}}_{| {{{{{{{\mathcal{E}}}}}}}}| })$, where [r]_i = r_i ≥ 0 for $1\le i\le | {{{{{{{\mathcal{V}}}}}}}}|$, and ${[{{{{{{{{\bf{n}}}}}}}}}_{e}]}_{k}={n}_{e,k}\in \{0,1\}$ for $1\le e\le | {{{{{{{\mathcal{E}}}}}}}}|$ and 1 ≤ k ≤ K_e, such that $\mathop{\sum }\nolimits_{i = 1}^{| {{{{{{{\mathcal{V}}}}}}}}| }{r}_{i}+\mathop{\sum }\nolimits_{e = 1}^{| {{{{{{{\mathcal{E}}}}}}}}| }\mathop{\sum }\nolimits_{k = 1}^{{K}_{e}}{n}_{e,k}=N$. The restriction n_e,k ∈ {0, 1} is necessary to enforce volume exclusion for individuals in the lattice sites along the narrow channels.

For the FMM the population evolves as follows. An individual occupying any lattice site within any narrow channel, attempts to jump to an adjacent lattice site or reservoir at rate α. Individuals in the ith reservoir will attempt to jump into the first lattice site of a connecting narrow channel at rate ${\gamma }_{i}={\tau }_{i}^{-1}$, where τ_i is the mean exit time of the ith reservoir. Formally, the state vector S(t) evolves according to the following CTMC. An individual in narrow channel e occupying the kth lattice site, jumps to the adjacent lattice site k + 1 at rate $\alpha {N}_{e,k}(t)\left(1-{N}_{e,k+1}(t)\right)$ for 1 ≤ k ≤ K_e − 1. Note that this transition rate is zero if either the kth lattice site is empty, N_e,k(t) = 0, or the adjacent lattice site is occupied, N_e,k+1(t) = 1. An individual in lattice site K_e along the narrow channel e jumps into the reservoir connected to lattice site K_e at rate $\alpha {N}_{e,{K}_{e}}(t)$. Similarly, an individual occupying the kth lattice site along narrow channel e jumps to the adjacent site k−1 at rate $\alpha {N}_{e,k}(t)\left(1-{N}_{e,k-1}(t)\right)$ for 2 ≤ k ≤ K_e, and an individual in the first lattice site jumps into the connected reservoir at rate αN_e,1(t). Finally, an individual in the ith reservoir jumps into the first lattice site of a connected narrow channel e at rate ${\gamma }_{i}\left(1-{N}_{e,1}(t)\right)$ or ${\gamma }_{i}\left(1-{N}_{e,{K}_{e}}(t)\right)$ depending on the orientation of the narrow channel e. A transition matrix Q for the CTMC is constructed as follows. Let ${{{{{{{\mathcal{I}}}}}}}}\left({{{\Omega }}}_{N,{{{{{{{\mathcal{G}}}}}}}}}\right)$ be an index set, such that if $u\in {{{{{{{\mathcal{I}}}}}}}}\left({{{\Omega }}}_{N,{{{{{{{\mathcal{G}}}}}}}}}\right)$ then ${{{{{{{{\bf{s}}}}}}}}}_{u}\in {{{\Omega }}}_{N,{{{{{{{\mathcal{G}}}}}}}}}$. For $u,v\in {{{{{{{\mathcal{I}}}}}}}}\left({{{\Omega }}}_{N,{{{{{{{\mathcal{G}}}}}}}}}\right)$ and u ≠ v the matrix entry Q_u,v is equal to the rate at which state s_u transitions to state s_v, as detailed above. If a transition cannot occur via a single jump event the matrix entry Q_u,v is zero. The diagonal entries are equal to the negative of the row sums, Q_u,u = − ∑_v≠uQ_u,v for $1\le u\le | {{{\Omega }}}_{N,{{{{{{{\mathcal{G}}}}}}}}}|$. The reciprocal of the spectral gap of Q measures the equilibration time for a networked population of individuals.

Equilibrium occupancy

Here we derive an approximate formula for the equilibrium occupancy probability of a narrow channel lattice site. We define the single-site probability function ${\rho }_{i}^{(1)}\left(n,t\right)={\mathbb{P}}\left({R}_{i}(t)=n\right)$, to be the probability that the ith reservoir is occupied by n individuals at time t. Define ${\rho }_{e}^{(1)}\left(O(k),t\right)={\mathbb{P}}\left({N}_{e,k}(t)=1\right)$ to be the probability that the kth lattice site along narrow channel e is occupied, where 1 ≤ k ≤ K_e. Similarly, let ${\rho }_{e}^{(1)}\left({{\emptyset}}(k),t\right)={\mathbb{P}}\left({N}_{e,k}(t)=0\right)$ be the probability that the kth lattice site is vacant. For a network ${{{{{{{\mathcal{G}}}}}}}}=\{{{{{{{{\mathcal{V}}}}}}}},{{{{{{{\mathcal{E}}}}}}}}\}$, we seek a system of ordinary differential equations (ODEs) that describe the evolution of the single-site probability functions. For the ith reservoir let ${{{{{{{\mathcal{N}}}}}}}}(i)$ be the indices for the narrow channels that are connected at one end to the ith reservoir. For notational convenience suppose that every narrow channel connected to reservoir i has polarity such that the lattice site adjacent to reservoir i has index one. Define $\langle {R}_{i}(t)\rangle =\mathop{\sum }\nolimits_{n = 0}^{N}n{\rho }_{i}^{(1)}\left(n,t\right)$, to be the mean number of individuals in the ith reservoir at time t. Following the approach of Baker and Simpson⁷⁰ provides the ODEs

$$\frac{{{{{{{{\rm{d}}}}}}}}\langle {R}_{i}(t)\rangle }{{{{{{{{\rm{d}}}}}}}}t}=\alpha \mathop{\sum}\limits_{e\in {{{{{{{\mathcal{N}}}}}}}}(i)}{\rho }_{e}^{(1)}\left(O(1),t\right)-{\gamma }_{i}\mathop{\sum}\limits_{e\in {{{{{{{\mathcal{N}}}}}}}}(i)}\mathop{\sum }\limits_{n=0}^{N}n{\rho }_{i,e}^{(2)}\left(n,{{\emptyset}}(1),t\right),$$

(9a)

for $1\le i\le | {{{{{{{\mathcal{V}}}}}}}}|$, where ${\rho }_{i,e}^{(2)}\left(n,{{\emptyset}}(1),t\right)$ is the two-site probability that the ith reservoir is occupied by n individuals and the first lattice site along narrow channel e is vacant at time t. Similarly, the ODEs for the occupancy probabilities of the lattice sites of a narrow channel e connecting reservoirs i and j are

$$\frac{{{{{{{{\rm{d}}}}}}}}{\rho }_{e}^{(1)}\left(O(1),t\right)}{{{{{{{{\rm{d}}}}}}}}t}={\gamma }_{i}\mathop{\sum }\limits_{n=0}^{N}n{\rho }_{i,e}^{(2)}\left(n,{{\emptyset}}(1),t\right)+\alpha {\rho }_{e}^{(1)}\left(O(2),t\right)-2\alpha {\rho }_{e}^{(1)}\left(O(1),t\right),$$

(9b)

$$\frac{{{{{{{{\rm{d}}}}}}}}{\rho }_{e}^{(1)}\left(O(k),t\right)}{{{{{{{{\rm{d}}}}}}}}t}=\alpha {\rho }_{e}^{(1)}\left(O(k+1),t\right)+\alpha {\rho }_{e}^{(1)}\left(O(k-1),t\right)-2\alpha {\rho }_{e}^{(1)}\left(O(k),t\right),$$

(9c)

$$\frac{{{{{{{{\rm{d}}}}}}}}{\rho }_{e}^{(1)}\left(O({K}_{e}),t\right)}{{{{{{{{\rm{d}}}}}}}}t}={\gamma }_{j}\mathop{\sum }\limits_{n=0}^{N}n{\rho }_{j,e}^{(2)}\left(n,{{\emptyset}}({K}_{e}),t\right)+\alpha {\rho }_{e}^{(1)}\left(O({K}_{e}-1),t\right)-2\alpha {\rho }_{e}^{(1)}\left(O({K}_{e}),t\right){\!},$$

(9d)

for 2 ≤ k ≤ K_e − 1. We are interested in the equilibrium solutions to the single-site probability functions, but, to make progress, we first consider the equilibrium occupancy probabilities along the eth edge.

Define S(e, k) to be the set of indices for the configuration states where the kth lattice site on narrow channel e is occupied and the (k + 1)st lattice site is vacant. For u ∈ S(e, k), v(u) is the index of the configuration state identical to u but the individual in lattice site k now occupies lattice site k + 1. Note that Q_u,v(u) = Q_v(u),u = α, where Q is the transition matrix of the FMM. Through decomposition of the two-site probability functions into entries of the equilibrium distribution p(∞), i.e. the principal left eigenvector of Q, we can show that the following local flux conservation law holds

$${\rho }_{e}^{(2)}\left(O(k),{{\emptyset}}(k+1),\infty \right)={\rho }_{e}^{(2)}\left({{\emptyset}}(k),O(k+1),\infty \right),$$

(10)

as follows:

$$\alpha {\rho }_{e}^{(2)}\left(O(k),{{\emptyset}}(k+1),\infty \right)=\alpha \mathop{\sum}\limits_{u\in S(e,k)}{[\overrightarrow{p}(\infty )]}_{u}$$

(11a)

$$=\mathop{\sum}\limits_{u\in S(e,k)}{Q}_{u,v(u)}{[\overrightarrow{p}(\infty )]}_{u}$$

(11b)

$$=\mathop{\sum}\limits_{u\in S(e,k)}{Q}_{v(u),u}{[\overrightarrow{p}(\infty )]}_{v(u)}$$

(11c)

$$=\alpha \mathop{\sum}\limits_{u\in S(e,k)}{[\overrightarrow{p}(\infty )]}_{v(u)}$$

(11d)

$$=\alpha {\rho }_{e}^{(2)}\left({{\emptyset}}(k),O(k+1),\infty \right),$$

(11e)

where the equality between Eqs. (11b) and (11c) holds due to detailed balance. Due to a conservation of probability we have that

$${\rho }_{e}^{(2)}\left(O(k),{{\emptyset}}(k+1),\infty \right)={\rho }_{e}^{(1)}\left(O(k),\infty \right)-{\rho }_{e}^{(2)}\left(O(k),O(k+1),\infty \right),$$

(12)

and similarly

$${\rho }_{e}^{(2)}\left({{\emptyset}}(k),O(k+1),\infty \right)={\rho }_{e}^{(1)}\left(O(k+1),\infty \right)-{\rho }_{e}^{(2)}\left(O(k),O(k+1),\infty \right).$$

(13)

Combining Eqs. (10), (12) and (13), we have

$${\rho }_{e}^{(1)}\left(O(k),\infty \right)={\rho }_{e}^{(1)}\left(O(k+1),\infty \right),$$

(14)

for 1 ≤ k ≤ K_e − 1. Therefore, we have shown that

$${\rho }_{e}^{(1)}\left(O(k),\infty \right)={\rho }_{e}^{* },$$

(15)

for some constant ${\rho }_{e}^{* }$, for 1 ≤ k ≤ K_e.

Returning to the ODEs in Eq. (9a), we equate the right-hand side to zero to provide a set of algebraic equations for the single-site equilibrium probability functions in terms of the two-site equilibrium probability functions. We find that for two distinct reservoirs i and j connected by a narrow channel e, $\alpha {\rho }_{e}^{* }={\gamma }_{i}\mathop{\sum }\nolimits_{n = 0}^{N}n{\rho }_{i,e}^{(2)}\left(n,{{\emptyset}}(1),\infty \right)={\gamma }_{j}\mathop{\sum }\nolimits_{n = 0}^{N}n{\rho }_{j,e}^{(2)}\left(n,{{\emptyset}}({K}_{e}),\infty \right)$. Expressions for the two-site equilibrium probability functions, ${\rho }_{i,e}^{(2)}\left(n,{{\emptyset}}(1),\infty \right)$ and ${\rho }_{j,e}^{(2)}\left(n,{{\emptyset}}({K}_{e}),\infty \right)$, can be found by first writing down their time-dependent ODEs and solving the algebraic equations that arise by setting the time derivatives to zero, however the resulting expressions would in turn depend upon three-site probability functions. Instead, we close the system at the level of the two-site probability functions by making a moment-closure approximation⁷¹. Utilising the mean-field approximation (MFA)

$${\rho }_{i,e}^{(2)}\left(n,{{\emptyset}}(1),\infty \right)={\rho }_{i}^{(1)}\left(n,\infty \right){\rho }_{e}^{(1)}\left({{\emptyset}}(1),\infty \right),$$

(16)

yields

$$\alpha {\tilde{\rho }}_{e}^{* }={\gamma }_{i}\langle {R}_{i}(\infty )\rangle \left(1-{\tilde{\rho }}_{e}^{* }\right),$$

(17)

and similarly,

$$\alpha {\tilde{\rho }}_{e}^{* }={\gamma }_{j}\langle {R}_{j}(\infty )\rangle \left(1-{\tilde{\rho }}_{e}^{* }\right),$$

(18)

where ${\tilde{\rho }}_{e}^{* }$ denotes the approximation to the exact equilibrium densities ${\rho }_{e}^{* }$ due to the MFA. Therefore, γ_i〈R_i(∞)〉 = γ_j〈R_j(∞)〉 for directly connected reservoirs i and j. For a connected network there exists a path between all pairs of reservoirs, therefore γ_i〈R_i(∞)〉 is equal to some constant γ* for all reservoirs. Noting that $\alpha {\tilde{\rho }}_{e}^{* }={\gamma }^{* }\left(1-{\tilde{\rho }}_{e}^{* }\right)$ for all narrow channels e, reveals that the equilibrium density ${\tilde{\rho }}_{e}^{* }$ is equal to a constant ${\tilde{\rho }}^{* }={\gamma }^{* }/(\alpha +{\gamma }^{* })$ for all narrow channels. Combining $\mathop{\sum }\nolimits_{i = 1}^{| {{{{{{{\mathcal{V}}}}}}}}| }\langle {R}_{i}\rangle +{K}_{{{{{\rm{tot}}}}}}{\tilde{\rho }}^{* }=N$, and 〈R_i〉 = γ*/γ_i, yields ${\gamma }^{* }=\left(N-{K}_{{{{{\rm{tot}}}}}}{\tilde{\rho }}^{* }\right)h({{{{{{{\boldsymbol{\gamma }}}}}}}})/| {{{{{{{\mathcal{V}}}}}}}}|$, where [γ]_i = γ_i and h(γ) is the harmonic mean of the reservoir jump rates. Substituting the expression for γ* into ${\tilde{\rho }}^{* }={\gamma }^{* }/(\alpha +{\gamma }^{* })$, and noting that h(γ) = 〈τ〉⁻¹ where $\langle {{{{{{{\boldsymbol{\tau }}}}}}}}\rangle =\mathop{\sum }\nolimits_{i = 1}^{| {{{{{{{\mathcal{V}}}}}}}}| }{\tau }_{i}/| {{{{{{{\mathcal{V}}}}}}}}|$, results in the quadratic equation

$${K}_{{{{{\rm{tot}}}}}}{\left({\tilde{\rho }}^{* }\right)}^{2}-\left(\left(N+{K}_{{{{{\rm{tot}}}}}}\right)+\alpha | {{{{{{{\mathcal{V}}}}}}}}| \langle {{{{{{{\boldsymbol{\tau }}}}}}}}\rangle \right){\tilde{\rho }}^{* }+N=0.$$

(19)

Taking the smaller root of Eq. (19) (the only root between zero and one) yields

$${\tilde{\rho }}^{* }=\frac{\left(N+{K}_{{{{{\rm{tot}}}}}}\right)+\alpha | {{{{{{{\mathcal{V}}}}}}}}| \langle {{{{{{{\boldsymbol{\tau }}}}}}}}\rangle -\sqrt{{\left(\left(N+{K}_{{{{{\rm{tot}}}}}}\right)+\alpha | {{{{{{{\mathcal{V}}}}}}}}| \langle {{{{{{{\boldsymbol{\tau }}}}}}}}\rangle \right)}^{2}-4N{K}_{{{{{\rm{tot}}}}}}}}{2{K}_{{{{{\rm{tot}}}}}}}.$$

(20)

The validity of this analytical approximation to the equilibrium occupancy is explored in Supplementary Note 1 and Supplementary Fig. 1.

High-density condition

For the approximate equilibrium density ${\tilde{\rho }}^{* }$, let ${\tilde{\rho }}^{* }=1-\varepsilon$ where ε ≪ 1 to ensure that the narrow channel equilibrium occupancy is high. Linearising Eq. (19) and solving in terms of ε, yields $\varepsilon =\alpha | {{{{{{{\mathcal{V}}}}}}}}| \langle {{{{{{{\boldsymbol{\tau }}}}}}}}\rangle /\left(\left(N-{K}_{{{{{\rm{tot}}}}}}\right)+\alpha | {{{{{{{\mathcal{V}}}}}}}}| \langle {{{{{{{\boldsymbol{\tau }}}}}}}}\rangle \right)$. As ε ≪ 1 we must have $\langle {{{{{{{\boldsymbol{\tau }}}}}}}}\rangle \ll \left(N-{K}_{{{{{\rm{tot}}}}}}\right)/\left(\alpha | {{{{{{{\mathcal{V}}}}}}}}| \right)$.

Reduced Markov model

In this section, we present the derivation of the RMM. We derive the transition rates ${k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({{{{{{{\bf{n}}}}}}}}\right)$ of individuals between adjacent reservoirs i and j by studying the time taken for an individual to be exchanged between the reservoirs. We refer to this time as the vacancy switching time as it is more convenient to invoke particle–hole duality⁵³ and model the dynamics of a vacant site rather than the interacting individuals themselves.

Consider an initial configuration of individuals where every lattice site along a narrow channel connecting reservoirs i and j are occupied, and n_i and n_j individuals occupy the ith and jth reservoirs, respectively. The only attempted movements affecting the narrow channel (i,j) that are not blocked by exclusion are either the individual in lattice site one jumps into the ith reservoir, or the individual in lattice site K_(i,j) jumps into the jth reservoir, and both jumps occur at rate α. In the latter case, the jth reservoir is occupied by n_j + 1 individuals and lattice site K_(i,j) becomes vacant. The rate at which the vacant lattice site K_(i,j) is re-occupied by an individual from the jth reservoir is γ_j(n_j + 1), and this competes with the rate α, the rate at which the individual in lattice site K_(i,j) − 1 jumps into lattice site K_(i,j). In the high-density regime the vacant lattice site K_(i,j) is almost immediately re-occupied by an individual from the jth reservoir and no exchange of individuals occurs. However, eventually the individual in lattice site K_(i,j) − 1 will jump before any individual in the jth reservoir, resulting in a vacancy at lattice site K_(i,j) − 1.

Let the lattice sites with indices between two and K_(i,j) − 1 be referred to as the internal lattice sites of the narrow channel. Then ${T}_{i,j}^{\,{{{{\rm{enter}}}}}\,}$ is the time taken for a vacancy to first enter the internal lattice sites of the narrow channel at the end connected to the jth reservoir. A vacancy in the internal lattice sites follows a symmetric random walk with jump rates α in both directions until eventually, at time ${T}_{i,j}^{\,{{{{\rm{absorb}}}}}\,}$, the vacancy reaches one of the end lattice sites of the channel, namely K_(i,j) or one. If the vacancy reaches lattice site K_(i,j) then almost immediately an individual in the jth reservoir jumps into lattice site K_(i,j) and there is no exchange of an individual between the two reservoirs. However, if a vacancy reaches lattice site one then almost immediately an individual in the ith reservoir jumps into lattice site one. However, there are now n_i − 1 and n_j + 1 individuals in the ith and jth reservoirs, respectively, and an individual has been exchanged between the ith and jth reservoirs. A vacancy at lattice site K_(i,j) − 1 hits lattice site one before lattice site K_(i,j) with probability 1/(K_(i,j) − 1). Therefore, the number of attempts before the vacancy is absorbed at lattice site one, G_i,j, is geometrically distributed with success probability 1/(K_(i,j) − 1).

The time taken for a vacancy to enter the internal lattice sites at lattice site K_(i,j) − 1 and subsequently reach lattice site one, is referred to as the vacancy switching time and is denoted by ${T}_{i,j}^{\,{{{{\rm{switch}}}}}\,}({n}_{j})$. The vacancy switching time is expressed as the following random sum

$${T}_{i,j}^{\,{{{{\rm{switch}}}}}\,}({n}_{j})=\mathop{\sum }\limits_{k=1}^{{G}_{i,j}}\left({T}_{i,j}^{\,{{{{\rm{enter}}}}},k}+{T}_{i,j}^{{{{{\rm{absorb}}}}}\,,k}\right),$$

(21)

where ${T}_{i,j}^{\,{{{{\rm{enter}}}}},k}$ and ${T}_{i,j}^{\,{{{{\rm{absorb}}}}},k}$ are independent instances of the random variables ${T}_{i,j}^{\,{{{{\rm{enter}}}}}\,}$ and ${T}_{i,j}^{\,{{{{\rm{absorb}}}}}\,}$, respectively. Therefore, the RMM in the high-density regime is defined to have transition rates ${k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({{{{{{{\bf{n}}}}}}}}\right)={\left\langle {T}_{i,j}^{{{{{\rm{switch}}}}}}({n}_{j})\right\rangle }^{-1}$ for an individual to be exchanged from the ith to the jth reservoir.

The first moment of the vacancy switching time in Eq. (21) is

$$\left\langle {T}_{i,j}^{\,{{{{\rm{switch}}}}}\,}({n}_{j})\right\rangle =\langle {G}_{i,j}\rangle \left(\left\langle {T}_{i,j}^{\,{{{{\rm{enter}}}}}\,}\right\rangle +\left\langle {T}_{i,j}^{\,{{{{\rm{absorb}}}}}\,}\right\rangle \right),$$

(22)

where 〈G_i,j〉 = K_(i,j) − 1 and, from calculation of first passage times on a finite lattice⁵⁸, $\left\langle {T}_{i,j}^{\,{{{{\rm{absorb}}}}}\,}\right\rangle =({K}_{(i,j)}-2)/2\alpha$. Recall that ${T}_{i,j}^{\,{{{{\rm{enter}}}}}\,}$ is the time for a vacancy to enter lattice site K_(i,j) − 1. Initially every lattice site is full and the individual at lattice site K_(i,j) jumps into the jth reservoir after an exponentially distributed amount of time, X, with rate parameter α. Then either the individual in lattice site K_(i,j) − 1 jumps into lattice site K_(i,j) at rate α, or an individual in the jth reservoir jumps into lattice site K_(i,j) at rate γ_j(n_j + 1). The time taken for either jump to occur is exponentially distributed, Y, with rate parameter α + γ_j(n_j + 1). The vacancy at lattice site K_(i,j) enters lattice site K_(i,j) − 1 with probability $q=\alpha /\left(\alpha +{\gamma }_{j}({n}_{j}+1)\right)$, thus ${T}_{i,j}^{\,{{{{\rm{enter}}}}}\,}=\mathop{\sum }\nolimits_{k = 1}^{G(q)}{X}^{k}+{Y}^{k}$ where G(q) is a geometric random variable with success probability q and X^k and Y^k are independent instances of the exponential random variables with rate parameters α and α + γ_j(n_j + 1), respectively. The first moment of ${T}_{i,j}^{\,{{{{\rm{enter}}}}}\,}$ is

$$\left\langle {T}_{i,j}^{\,{{{{\rm{enter}}}}}\,}\right\rangle =\frac{\alpha +{\gamma }_{j}({n}_{j}+1)}{\alpha }\left(\frac{1}{\alpha }+\frac{1}{\alpha +{\gamma }_{j}({n}_{j}+1)}\right).$$

(23)

From Eq. (23), and recalling that $\Big\langle {T}_{i,j}^{\,{{{{\rm{switch}}}}}\,}({n}_{j})\Big\rangle =\langle {G}_{i,j}\rangle \Big(\Big\langle {T}_{i,j}^{\,{{{{\rm{enter}}}}}\,}\Big\rangle \,+\Big\langle {T}_{i,j}^{\,{{{{\rm{absorb}}}}}\,}\Big\rangle \Big)$, ${k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}({{{{{\bf{n}}}}}})={\left\langle {T}_{i,j}^{{{{{\rm{switch}}}}}}({n}_{j})\right\rangle }^{-1}$ and ${\tau }_{j}={\gamma }_{j}^{-1}$, the transition rates for the RMM in the high-density regime have the explicit formulae

$${k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}({{{{{\bf{n}}}}}})=\frac{1}{{K}_{(i,j)}-1}{\left(\frac{{\tau }_{j}^{-1}({n}_{j}+1)+2\alpha }{{\alpha }^{2}}+\frac{{K}_{(i,j)}-2}{2\alpha }\right)}^{-1},$$

(24)

for $1\le i \;\ne \; j\le | {{{{{{{\mathcal{V}}}}}}}}|$. The validity of the RMM depends on how accurately ${T}_{i,j}^{\,{{{{\rm{switch}}}}}\,}({n}_{j})$ is approximated by the exponential distribution with rate parameter ${k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}({{{{{{{\bf{n}}}}}}}})$, which is investigated in Supplementary Note 1.

Ornstein–Uhlenbeck process

In this section, we perform a coarse graining of the RMM in the high-density regime to yield an OU process that governs the exchange of individuals in a networked environment. To make progress we write down the chemical master equations that govern the RMM. Let the vector ν_i,j for $i \; \ne \; j\in \{1,\ldots ,| {{{{{{{\mathcal{V}}}}}}}}| \}$ be defined as ${[{{{{{{{{\boldsymbol{\nu }}}}}}}}}_{i,j}]}_{k}={\delta }_{j,k}-{\delta }_{i,k}$ for $1\le k\le | {{{{{{{\mathcal{V}}}}}}}}|$, where δ_j,k and δ_i,k are Kronecker deltas. A transition from state vector n to n + ν_i,j, corresponds to an exchange of a single individual from the ith to the jth reservoir. Such a transition can only occur if reservoirs i and j are directly connected via a narrow channel and occurs at rate ${k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({{{{{{{\bf{n}}}}}}}}\right)$ given in Eq. (24). Let the adjacency matrix ${{{{{{{\boldsymbol{{{{{{{{\mathcal{A}}}}}}}}}}}}}}}}$ be a $| {{{{{{{\mathcal{V}}}}}}}}| \times | {{{{{{{\mathcal{V}}}}}}}}|$ matrix with entry ${{{{{{{{\mathcal{A}}}}}}}}}_{i,j}$ equal to one if a narrow channel connecting reservoirs i and j is present in the network, and zero otherwise. Additionally, define p(n, t) to be the probability that the individuals are distributed amongst the reservoirs with state vector n at time t. The chemical master equations governing the evolution of p(n, t) are

$$\frac{{{{{{{{\rm{d}}}}}}}}p({{{{{{{\bf{n}}}}}}}},t)}{{{{{{{{\rm{d}}}}}}}}t}=\mathop{\sum }\limits_{i=1}^{| {{{{{{{\mathcal{V}}}}}}}}| }\mathop{\sum }\limits_{j=1}^{| {{{{{{{\mathcal{V}}}}}}}}| }{{{{{{{{\mathcal{A}}}}}}}}}_{i,j}\left\{{k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({{{{{{{\bf{n}}}}}}}}-{{{{{{{{\boldsymbol{\nu }}}}}}}}}_{i,j}\right)p({{{{{{{\bf{n}}}}}}}}-{{{{{{{{\boldsymbol{\nu }}}}}}}}}_{i,j},t)-{k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({{{{{{{\bf{n}}}}}}}}\right)p({{\bf{n}}},t)\right\},$$

(25)

where ${k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({{{{{{{\bf{n}}}}}}}}\right)=0$, when n_i = N_HD or n_j = 0 to avoid transitions to states with non-negative entries, or entries that exceed the total population N_HD = N − K_tot.

Fokker–Planck equation

To derive the Fokker–Planck equation corresponding to Eq. (25), we introduce ${{{{{{{\bf{x}}}}}}}}=({x}_{1},\ldots ,{x}_{| {{{{{{{\mathcal{V}}}}}}}}| })$, where x_i = n_i/N_HD is the fraction of the population that occupies the ith reservoir. For N_HD ≫ 1, the fractions x_i are approximately continuous and lie in the interval [0, 1]. Introducing Q(x, t) = p(n, t) and performing a Taylor expansion in ϵ = 1/N_HD of Eq. (25), yields the linear Fokker–Planck equation

$$\frac{\partial Q({{{{{{{\bf{x}}}}}}}},t)}{\partial t}=\mathop{\sum }\limits_{i=1}^{| {{{{{{{\mathcal{V}}}}}}}}| }\mathop{\sum }\limits_{j=1}^{| {{{{{{{\mathcal{V}}}}}}}}| }{{{{{{{{\mathcal{A}}}}}}}}}_{i,j}\left\{\epsilon {\nabla }_{i,j}\left[{g}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({{{{{{{\bf{x}}}}}}}}\right)Q({{{{{{{\bf{x}}}}}}}},t)\right]+\frac{{\epsilon }^{2}}{2}{\nabla }_{i,j}^{2}\left[{g}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({{{{{{{\bf{x}}}}}}}}\right)Q({{{{{{{\bf{x}}}}}}}},t)\right]\right\},$$

(26)

where ${g}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({{{{{{{\bf{x}}}}}}}}\right)={k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({N}_{{{{{\rm{HD}}}}}}{{{{{{{\bf{x}}}}}}}}\right)$. The operator ∇_i,j is defined as ∂/∂x_i − ∂/∂x_j, and the partial differential equation (PDE) in Eq. (26) is defined on the domain ${{{{{{{\bf{x}}}}}}}}\in {[0,1]}^{| {{{{{{{\mathcal{V}}}}}}}}| }$, with zero-flux boundary conditions.

Equilibrium vector

The equilibrium vector x*, is the distribution of individuals that satisfies the following equations:

$$\mathop{\sum }\limits_{j=1}^{| {{{{{{{\mathcal{V}}}}}}}}| }{{{{{{{{\mathcal{A}}}}}}}}}_{i,j}\left[{g}_{i,j}^{\,{{{{\rm{HD}}}}}\,}({{{{{{{{\bf{x}}}}}}}}}^{* })-{g}_{j,i}^{\,{{{{\rm{HD}}}}}\,}({{{{{{{{\bf{x}}}}}}}}}^{* })\right]=0,$$

(27)

for $1\le i\le | {{{{{{{\mathcal{V}}}}}}}}|$. Eq. (27) is known as the global balance equation. The distribution of individuals x* that solves the global balance equations is such that the total transition rate out of each reservoir is equal to the total transition rate in. For large N_HD the rate functions are approximately given by ${g}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({{{{{{{{\bf{x}}}}}}}}}^{* }\right)\approx {\alpha }^{2}{\tau }_{j}/\left(\left({K}_{(i,j)}-1\right){N}_{{{{{\rm{HD}}}}}}{x}_{j}^{* }\right)$. Substituting this approximation into Eq. (27), yields the following system of equations:

$$\frac{{\alpha }^{2}}{{N}_{{{{{\rm{HD}}}}}}}\mathop{\sum }\limits_{j=1}^{| {{{{{{{\mathcal{V}}}}}}}}| }\frac{{{{{{{{{\mathcal{A}}}}}}}}}_{i,j}}{{K}_{(i,j)}-1}\left(\frac{{\tau }_{j}}{{x}_{j}^{* }}-\frac{{\tau }_{i}}{{x}_{i}^{* }}\right)=0,$$

(28)

for $1\le i\le | {{{{{{{\mathcal{V}}}}}}}}|$. For b such that ${[{{{{{{{\bf{b}}}}}}}}]}_{i}={\tau }_{i}/{x}_{i}^{* }$ and M such that for i ≠ j, ${M}_{i,j}={{{{{{{{\mathcal{A}}}}}}}}}_{i,j}/\left({K}_{(i,j)}-1\right)$ and ${M}_{i,i}=-\mathop{\sum }\nolimits_{j\ne i}^{| {{{{{{{\mathcal{V}}}}}}}}| }{M}_{i,j}$, Eq. (28) is equivalent to Mb = 0. For a connected network the null space of M is spanned by the constant vector and, along with the condition that $\mathop{\sum }\nolimits_{i = 1}^{| {{{{{{{\mathcal{V}}}}}}}}| }{x}_{i}^{* }=1$, the unique solution to Eq. (28) is given by ${x}_{i}^{* }={\tau }_{i}/\mathop{\sum }\nolimits_{k = 1}^{| {{{{{{{\mathcal{V}}}}}}}}| }{\tau }_{k}$ for $1\le i\le | {{{{{{{\mathcal{V}}}}}}}}|$.

Localising the Fokker–Planck equation

To extract an equilibration time from the Fokker–Planck equation in Eq. (26), we localise the PDE about the equilibrium vector. Let z be a perturbation about the equilibrium vector, such that x = x* + z and ∣z_i∣ ≪ 1 for $1\le i\le | {{{{{{{\mathcal{V}}}}}}}}|$. Introducing $\tilde{Q}({{{{{{{\bf{z}}}}}}}},t)=Q({{{{{{{\bf{x}}}}}}}},t)$ and localising Eq. (26) about x* yields

$$\frac{\partial \tilde{Q}({{{{{\bf{z}}}}}},t)}{\partial t}=\; \epsilon \mathop{\sum }\limits_{i=1}^{| {{{{{\mathcal{V}}}}}}| }\frac{\partial \tilde{Q}}{\partial {z}_{i}}\left\{\mathop{\sum }\limits_{j=1}^{| {{{{{\mathcal{V}}}}}}| }{{{{{{\mathcal{A}}}}}}}_{i,j}\left[{g}_{i,j}^{\,{{{{\rm{HD}}}}}\,}({{{{{{\bf{x}}}}}}}^{* })-{g}_{j,i}^{\,{{{{\rm{HD}}}}}\,}({{{{{{\bf{x}}}}}}}^{* })\right]\right\}\\ +\epsilon \mathop{\sum }\limits_{i=1}^{| {{{{{\mathcal{V}}}}}}| }\frac{\partial }{\partial {z}_{i}}\left\{\left[\left(\mathop{\sum }\limits_{j=1}^{| {{{{{\mathcal{V}}}}}}| }{{{{{{\mathcal{A}}}}}}}_{i,j}{\left({g}_{i,j}^{{{{{\rm{HD}}}}}}\right)}^{\prime}({{{{{{\bf{x}}}}}}}^{* }){z}_{j}\right)-\left(\mathop{\sum }\limits_{j=1}^{| {{{{{\mathcal{V}}}}}}| }{{{{{{\mathcal{A}}}}}}}_{i,j}{\left({g}_{j,i}^{{{{{\rm{HD}}}}}}\right)}^{\prime}({{{{{{\bf{x}}}}}}}^{* })\right){z}_{i}\right]\tilde{Q}\right\}\\ +\frac{{\epsilon }^{2}}{2}\mathop{\sum }\limits_{i=1}^{| {{{{{\mathcal{V}}}}}}| }\frac{\partial }{\partial {z}_{i}}\left\{\mathop{\sum }\limits_{j=1}^{| {{{{{\mathcal{V}}}}}}| }{{{{{{\mathcal{A}}}}}}}_{i,j}\left[{g}_{i,j}^{\,{{{{\rm{HD}}}}}\,}({{{{{{\bf{x}}}}}}}^{* })+{g}_{j,i}^{\,{{{{\rm{HD}}}}}\,}({{{{{{\bf{x}}}}}}}^{* })\right]\left(\frac{\partial }{\partial {z}_{i}}-\frac{\partial }{\partial {z}_{j}}\right)\tilde{Q}\right\}.$$

(29)

Note that the first bracketed term on the right-hand side of Eq. (29) is equal to zero from Eq. (27). Adopting Einstein summation notation, Eq. (29) can be rewritten as

$$\frac{\partial \tilde{Q}(\overrightarrow{z},t)}{\partial t}={F}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\frac{\partial }{\partial {z}_{i}}\left[{z}_{j}\tilde{Q}\right]+{D}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\frac{{\partial }^{2}\tilde{Q}}{\partial {z}_{i}\partial {z}_{j}},$$

(30)

with zero-flux boundary conditions at z_i → ±∞, where ${F}_{i,j}^{\,{{{{\rm{HD}}}}}\,}$ and ${D}_{i,j}^{\,{{{{\rm{HD}}}}}\,}$ are entries of the drift and diffusion matrices, F^HD and D^HD, respectively. The entries of the drift matrix F^HD are

$${F}_{i,j}^{\,{{{{\rm{HD}}}}}\,}=\epsilon {{{{{{{{\mathcal{A}}}}}}}}}_{i,j}{\left({g}_{i,j}^{{{{{\rm{HD}}}}}}\right)}^{\prime}({{{{{{{{\bf{x}}}}}}}}}^{* }),$$

(31a)

for i ≠ j, and

$${F}_{i,i}^{\,{{{{\rm{HD}}}}}\,}=-\epsilon \mathop{\sum }\limits_{j=1}^{| {{{{{{{\mathcal{V}}}}}}}}| }{{{{{{{{\mathcal{A}}}}}}}}}_{i,j}{\left({g}_{j,i}^{{{{{\rm{HD}}}}}}\right)}^{\prime}({{{{{{{{\bf{x}}}}}}}}}^{* }),$$

(31b)

for $1\le i\le | {{{{{{{\mathcal{V}}}}}}}}|$. The entries of the diffusion matrix D^HD are

$${D}_{i,j}^{\,{{{{\rm{HD}}}}}\,}=-\frac{{\epsilon }^{2}}{2}{{{{{{{{\mathcal{A}}}}}}}}}_{i,j}\left({g}_{i,j}^{\,{{{{\rm{HD}}}}}\,}({{{{{{{{\bf{x}}}}}}}}}^{* })+{g}_{j,i}^{\,{{{{\rm{HD}}}}}\,}({{{{{{{{\bf{x}}}}}}}}}^{* })\right),$$

(32a)

for i ≠ j, and

$${D}_{i,i}^{\,{{{{\rm{HD}}}}}\,}=\frac{{\epsilon }^{2}}{2}\mathop{\sum }\limits_{j=1}^{| {{{{{{{\mathcal{V}}}}}}}}| }{{{{{{{{\mathcal{A}}}}}}}}}_{i,j}\left({g}_{i,j}^{\,{{{{\rm{HD}}}}}\,}({{{{{{{{\bf{x}}}}}}}}}^{* })+{g}_{j,i}^{\,{{{{\rm{HD}}}}}\,}({{{{{{{{\bf{x}}}}}}}}}^{* })\right),$$

(32b)

for $1\le i\le | {{{{{{{\mathcal{V}}}}}}}}|$. The PDE in Eq. (30) is in the form of a linear Fokker–Planck equation for a multivariate OU process for which the full probability distribution is known⁵⁴. Given an initial configuration of individuals x₀ the configuration of individuals at time t is normally distributed with mean vector μ(t; x₀) and covariance matrix Σ(t; x₀), given by

$${{{{{{{\boldsymbol{\mu }}}}}}}}(t;{{{{{{{{\bf{x}}}}}}}}}_{0})=\exp \left(-t{{{{{{{{\bf{F}}}}}}}}}^{{{{{\rm{HD}}}}}}\right){{{{{{{{\bf{x}}}}}}}}}_{0}+\left({{{{{{{\bf{I}}}}}}}}-\exp \left(-t{{{{{{{{\bf{F}}}}}}}}}^{{{{{\rm{HD}}}}}}\right)\right){{{{{{{{\bf{x}}}}}}}}}^{* },$$

(33)

and

$${{{{{{{\boldsymbol{\Sigma }}}}}}}}(t;{{{{{{{{\bf{x}}}}}}}}}_{0})=\int\nolimits_{0}^{t}\exp \left(-u{{{{{{{{\bf{F}}}}}}}}}^{{{{{\rm{HD}}}}}}\right){{{{{{{{\bf{D}}}}}}}}}^{{{{{\rm{HD}}}}}}\exp \left(-u{\left({{{{{{{{\bf{F}}}}}}}}}^{{{{{\rm{HD}}}}}}\right)}^{T}\right){{{{{{{\rm{d}}}}}}}}u,$$

(34)

respectively, where I is the identity matrix. The timescale upon which the moments decay to equilibrium is dictated by the spectral gap of F^HD. Additionally, multiplying Eq. (30) by each z_i in turn and integrating over ${\mathbb{R}}^{|{{\mathcal{V}}}|}$ yields dμ(t)/dt = −F^HDμ(t). This system of ODEs is reminiscent of the system of ODEs that governs the evolution of the probability distribution for a CTMC and therefore we can view the networked graph Laplacian as effectively being a transition rate matrix.

Tagged individual crossing probability

In this section, we provide the technical details for the derivation of the tagged individual crossing probability. Let distinct reservoirs i and j be connected by a narrow channel of length K_(i,j) such that the site with index one is adjacent to the ith reservoir and the site with index K_(i,j) is adjacent to the jth reservoir. We consider the probability that a tagged individual, initially in the second lattice site of a narrow channel connecting the ith and jth reservoirs (Fig. 4a), which are occupied by n_i and n_j background individuals, respectively, reaches the site with index K_(i,j) before the site with index one. We note that, just as for the vacancy switching time, as soon as a tagged individual reaches a non-internal lattice site (either site one or K_(i,j)) it is considered to have reached the adjacent reservoir. However, unlike the dynamics of a vacancy, the probability that a tagged individual moves towards the ith or jth reservoir is not symmetric as it depends on the rates ${k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}({{{{{{{\bf{n}}}}}}}})$ and ${k}_{j,i}^{\,{{{{\rm{HD}}}}}\,}({{{{{{{\bf{n}}}}}}}})$. Furthermore, these transition rates will change as the tagged individual walks along the narrow channel reflecting the change in the configuration of the background individuals. To make progress on this complex first-passage problem we formulate it as a recurrence relation.

Let q_i→j(k) be the probability that a background individual is exchanged from the ith to the jth reservoir before an exchange in the opposing direction, whilst the occupancies of the ith and jth reservoirs are n_i + 2 − k and n_j + k − 2, respectively. The index k corresponds to the position of the tagged individual, and for k = 2 the occupancy of the reservoirs is n_i and n_j. Additionally, let ${p}_{k}^{\,{{{{\rm{cross}}}}}\,}({n}_{i},{n}_{j})$ be the probability that the tagged individual reaches site K_(i,j) (the site adjacent to the jth reservoir) before site one (the site adjacent to the ith reservoir), given that it is initially at site k and the occupancy of the two reservoirs is n_i + 2 − k and n_j + k − 2, respectively. Then we can write down the recurrence relation

$${p}_{k}^{\,{{{{\rm{cross}}}}}}({n}_{i},{n}_{j})={q}_{i\to j}(k){p}_{k+1}^{{{{{\rm{cross}}}}}\,}({n}_{i},{n}_{j})+\left(1-{q}_{i\to j}(k)\right){p}_{k-1}^{\,{{{{\rm{cross}}}}}\,}({n}_{i},{n}_{j}),$$

(35)

for 2 ≤ k ≤ K_(i,j) − 1, where ${p}_{1}^{\,{{{{\rm{cross}}}}}\,}=0$ and ${p}_{{K}_{(i,j)}}^{\,{{{{\rm{cross}}}}}\,}=1$. Manipulating Eq. (35) yields

$${p}_{k+1}^{\,{{{{\rm{cross}}}}}}({n}_{i},{n}_{j})-{p}_{k}^{{{{{\rm{cross}}}}}\,}({n}_{i},{n}_{j})=\frac{\left(1-{q}_{i\to j}(k)\right)}{{q}_{i\to j}(k)}\left({p}_{k}^{\,{{{{\rm{cross}}}}}}({n}_{i},{n}_{j})-{p}_{k-1}^{{{{{\rm{cross}}}}}\,}({n}_{i},{n}_{j})\right).$$

(36)

Defining ${r}_{k}({n}_{i},{n}_{j})={p}_{k}^{\,{{{{\rm{cross}}}}}}({n}_{i},{n}_{j})-{p}_{k-1}^{{{{{\rm{cross}}}}}\,}({n}_{i},{n}_{j})$ reduces the recurrence relation in Eq. (36) to a first order recurrence relation with solution

$${r}_{k}({n}_{i},{n}_{j})={r}_{2}({n}_{i},{n}_{j})\mathop{\prod }\limits_{\ell =2}^{k-1}\left(\frac{1-{q}_{i\to j}(\ell )}{{q}_{i\to j}(\ell )}\right).$$

(37)

Noting that $\mathop{\sum }\nolimits_{k = 2}^{{K}_{(i,j)}}{r}_{k}({n}_{i},{n}_{j})={p}_{{K}_{(i,j)}}^{\,{{{{\rm{cross}}}}}\,}({n}_{i},{n}_{j})=1$ and ${r}_{2}({n}_{i},{n}_{j})={p}_{2}^{\,{{{{\rm{cross}}}}}\,}({n}_{i},{n}_{j})$ reveals that

$${p}_{2}^{\,{{{{\rm{cross}}}}}\,}({n}_{i},{n}_{j})={\left[1+\mathop{\sum }\limits_{k = 3}^{{K}_{(i,j)}}\mathop{\prod }\limits_{\ell = 2}^{k-1}\left(\frac{1-{q}_{i\to j}(\ell )}{{q}_{i\to j}(\ell )}\right)\right]}^{-1},$$

(38)

where ${p}_{2}^{\,{{{{\rm{cross}}}}}\,}({n}_{i},{n}_{j})$ is the tagged individual crossing probability. We note that the transition rates ${k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({{{{{{{\bf{n}}}}}}}}\right)$ depend upon the occupancy of the jth reservoir only, as such we redefine ${k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({n}_{j}\right)={k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({{{{{{{\bf{n}}}}}}}}\right)$. Recall that q_i→j(k) is the probability that a background individual is exchanged from the ith to the jth reservoir before an exchange in the opposing direction, whilst the occupancies of the ith and jth reservoirs are n_i + 2−k and n_j + k−2, respectively. Therefore,

$${q}_{i\to j}(k)=\frac{{k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({n}_{j}+k-2\right)}{{k}_{i,j}^{\,{{{{\rm{HD}}}}}\,}\left({n}_{j}+k-2\right)+{k}_{j,i}^{\,{{{{\rm{HD}}}}}\,}\left({n}_{i}+2-k\right)} \sim \frac{{\tau }_{i}^{-1}\left({n}_{i}+3-k\right)}{{\tau }_{i}^{-1}\left({n}_{i}+3-k\right)+{\tau }_{j}^{-1}\left({n}_{j}+k-1\right)},$$

(39)

where the asymptote in Eq. (39) comes from Eq. (24) for large populations. Substituting the right-hand side of Eq. (39) into Eq. (38) and rewriting the product in Eq. (38) in terms of Beta functions yields

$${p}_{2}^{\,{{{{\rm{cross}}}}}\,}({n}_{i},{n}_{j}) \sim {\left[1+\frac{\mathop{\sum }\nolimits_{k = 3}^{{K}_{(i,j)}}{\left(\frac{{\tau }_{i}}{{\tau }_{j}}\right)}^{k-2}{{{{{{{\rm{B}}}}}}}}\left({n}_{j}+k-1,{n}_{i}+4-k\right)}{{{{{{{{\rm{B}}}}}}}}\left({n}_{j}+1,{n}_{i}+2\right)}\right]}^{-1}.$$

(40)

Finally, letting x_i = n_i/N_HD and noting that ${{{{{{{\rm{B}}}}}}}}(x,y) \sim \sqrt{2\pi }{x}^{x-1/2}{y}^{y-1/2}/{\left(x+y\right)}^{x+y-1/2}$, a corollary of Stirling’s approximation, we arrive at an expression for ${p}_{{{{{\rm{TI}}}}}}\left({x}_{i},{x}_{j};{K}_{(i,j)}\right)$, the tagged individual crossing probability

$${p}_{{{{{\rm{TI}}}}}}\left({x}_{i},{x}_{j};{K}_{(i,j)}\right) \sim {f}_{0}\left({x}_{i},{x}_{j}\right){\left[\mathop{\sum }\limits_{k = 0}^{{K}_{(i,j)}-2}{f}_{k}\left({x}_{i},{x}_{j}\right)\right]}^{-1},$$

(41)

where the functions ${f}_{k}\left({x}_{i},{x}_{j}\right)$ are given by

$${f}_{k}\left({x}_{i},{x}_{j}\right)= \;{\left(\frac{{\tau }_{i}}{{\tau }_{j}}\right)}^{k}{\left(\frac{{x}_{i}}{{x}_{i}+{x}_{j}}+\frac{2-k}{{N}_{{{{{\rm{HD}}}}}}\left({x}_{i}+{x}_{j}\right)}\right)}^{{N}_{{{{{\rm{HD}}}}}}{x}_{i}+3/2-k} \\ \times{\left(\frac{{x}_{j}}{{x}_{i}+{x}_{j}}+\frac{1+k}{{N}_{{{{{\rm{HD}}}}}}\left({x}_{i}+{x}_{j}\right)}\right)}^{{N}_{{{{{\rm{HD}}}}}}{x}_{j}+1/2+k}.$$

(42)

Tagged individual mean exit time

The derivation of the average time taken for the tagged individual initially at the second lattice site to leave the narrow channel by reaching either site one or K_(i,j) is very similar to the tagged individual crossing probability. Firstly, let ${E}_{k}^{\,{{{{\rm{exit}}}}}\,}({n}_{i},{n}_{j})$ be the expected time taken for the tagged individual initially at lattice site k to exit the narrow channel when the occupancies of the ith and jth reservoirs are n_i + 2 − k and n_j + k − 2, respectively. The expected exit times ${E}_{k}^{\,{{{{\rm{exit}}}}}\,}({n}_{i},{n}_{j})$ obey the following recurrence relation:

$${E}_{k}^{\,{{{{\rm{exit}}}}}}({n}_{i},{n}_{j})={q}_{i\to j}(k){E}_{k+1}^{{{{{\rm{exit}}}}}\,}({n}_{i},{n}_{j})+\left(1-{q}_{i\to j}(k)\right){E}_{k-1}^{\,{{{{\rm{exit}}}}}\,}({n}_{i},{n}_{j})+{T}_{k}({n}_{i},{n}_{j}),$$

(43)

where ${T}_{k}({n}_{i},{n}_{j})={\left({k}_{i,j}^{{{{{\rm{HD}}}}}}\left({n}_{j}+k-2\right)+{k}_{j,i}^{{{{{\rm{HD}}}}}}\left({n}_{i}+2-k\right)\right)}^{-1}$ is the average time taken for a background individual exchange event to occur across the narrow channel connecting the ith and jth reservoirs when they have occupancies n_i + k − 2 and n_j + 2 − k, respectively. Repeating a near identical analysis of Eq. (43) as was seen for the tagged individual crossing probability yields an expression for ${m}_{{{{{\rm{TI}}}}}}\left({x}_{i},{x}_{j};{K}_{(i,j)}\right)={E}_{2}^{\,{{{{\rm{exit}}}}}\,}\left({N}_{{{{{\rm{HD}}}}}}{x}_{i},{N}_{{{{{\rm{HD}}}}}}{x}_{j}\right)$, the tagged individual mean exit time

$${m}_{{{{{\rm{TI}}}}}}\left({x}_{i},{x}_{j};{K}_{(i,j)}\right) \sim {p}_{{{{{\rm{TI}}}}}}\left({x}_{i},{x}_{j};{K}_{(i,j)}\right)\left[{h}_{1}\left({x}_{j}\right)+\mathop{\sum }\limits_{k=2}^{{K}_{(i,j)}-2}\mathop{\sum }\limits_{\ell =1}^{k}\frac{{h}_{\ell }({x}_{j}){f}_{k}\left({x}_{i},{x}_{j}\right)}{{f}_{\ell }\left({x}_{i},{x}_{j}\right)}\right],$$

(44)

where ${h}_{\ell }({x}_{j})=\left({K}_{(i,j)}-1\right)\left({N}_{{{{{\rm{HD}}}}}}{x}_{j}+\ell \right)/\left({\tau }_{j}{\alpha }^{2}\right)$, and the ${f}_{k}\left({x}_{i},{x}_{j}\right)$ are as in Eq. (42).