Spin-coupling-induced Improper Polarizations and Latent Magnetization in Multiferroic BiFeO₃

Abstract

Multiferroic BiFeO₃ (BFO) that exhibits a gigantic off-centering polarization (OCP) is the most extensively studied material among all multiferroics. In addition to this gigantic OCP, the BFO having R3c structural symmetry is expected to exhibit a couple of parasitic improper polarizations owing to coexisting spin-polarization coupling mechanisms. However, these improper polarizations are not yet theoretically quantified. Herein, we show that there exist two distinct spin-coupling-induced improper polarizations in the R3c BFO on the basis of the Landau-Lifshitz-Ginzburg theory: ΔP _LF arising from the Lifshitz gradient coupling in a cycloidal spin-density wave, and ΔP _ms originating from the biquadratic magnetostrictive interaction. With the help of ab initio calculations, we have numerically evaluated magnitudes of these improper polarizations, in addition to the estimate of all three relevant coupling constants. We further predict that the magnetic susceptibility increases substantially upon the transition from the bulk R3c BFO to the homogeneous canted spin state in a constrained epitaxial film, which satisfactorily accounts for the experimental observation. The present study will help us understand the magnetoelectric coupling and shed light on design of BFO-based materials with improved multiferroic properties.

Introduction

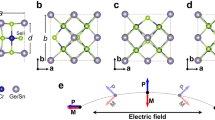
Multiferroics are an interesting group of materials that exhibit both ferroelectricity and anti-ferromagnetism with coupled electric and magnetic order parameters^1,2. Multiferroism is the subject of intensive scientific investigations as these materials are able to offer a wide range of interesting applications that include sensors, transducers, memories, spintronics and ferroelectric photovoltaics^{3,4,5,6,7,8,9}. Among numerous multiferroics, BiFeO₃ (BFO) is currently the only ABO₃-type simple perovskite that exhibits room-temperature multiferroism and, thus, is considered to be the most promising candidate for practical applications of multiferroics. It is a rhombohedrally distorted ferroelectric perovskite (T _c  ≈ 1100 K) with the space group R3c and shows canted antiferromagnetism up to 643 K (Néel temperature, T _N )^10,11,12. The R3c BFO is known to possess the largest reported value of the switchable polarization of ~90 μC/cm ² along the pseudo-cubic [111]_c direction (or equivalently, [001]_h in hexagonal notation; Fig. 1)^13,14. According to the previous ab initio studies^14,15,16,17, the stereochemically active lone-pair electrons originating from the hybridization of 6s and 6p atomic orbitals of Bi are responsible for the off-centering displacement (OCD) of the Bi ion along [111]_c (or [001]_h). Interestingly, the R3c BFO is further characterized by the incommensurate cycloidal spin structure with a periodicity of 620 Å along the [110]_h direction in hexagonal setting^18,19.

Figure 1

A half unit-cell hexagonal structure of BiFeO₃ having R3c space-group symmetry. The hexagonal lattice parameters shown in the figure (a = b = 5.580 Å, c = 13.872 Å) are based on our previous Rietveld refinement¹⁷. In the same figure, a pseudo-cubic representation is also shown along the [111]_c direction which is equivalent to the polar [001]_h direction in hexagonal notation.

The magnetoelectric (ME) coupling between polarization (P) and magnetization (M) order parameters is the single most important subject of multiferroics². In case of the R3c BFO, strong ME coupling is not anticipated due to the absence of a strong interaction between the ferroelectric OCD at the Bi-ion site and the G-type antiferromagnetic (AFM) spin moment at the Fe-ion site. However, the G-type AFM alignment plus the cycloidal spin ordering of BFO allows opportunities for interfacial magnetic coupling in multiferroic heterostructures, where BFO plays some important roles as ferroelectric substrate, AFM pinning layer for exchange bias, and interfacial quantum modulation donor². Indeed, Saenrang and co-workers²⁰ recently demonstrated deterministic and robust room-temperature exchange coupling between the BFO AFM order and the Co overlayer with ~90° in-plane Co-moment rotation upon single-step ferroelectric switching of the monodomain BFO. This has important consequences for practical, low power non-volatile ME devices utilizing BFO²⁰.

In spite of extensive studies on the R3c BFO, however, possible ME coupling mechanisms and associated improper polarizations are not yet quantitatively resolved or lucidly explained. Herein, we show unequivocally that there exist two distinct spin-coupling-induced improper polarizations in the R3c BFO on the basis of the Landau-Lifshitz-Ginzburg phenomenological theory. These are: (i) a small parasitic improper polarization (ΔP _LF ) originating from the Lifshitz exchange coupling, which can be equated with the S _i  × S _j -type vector coupling induced polarization (ΔP _DM ) caused by the reverse Dzyaloshinskii-Moriya (DM) interaction, and (ii) a S _i  · S _j -type scalar coupling induced polarization (ΔP _ms ) caused by the biquadratic magnetostrictive exchange interaction. With the help of ab initio density-functional theory (DFT) calculations, we have evaluated magnitudes of these improper polarizations, in addition to the numerical estimate of all three relevant ME coupling constants. We have further predicted that the magnetic susceptibility increases substantially upon the transition from the bulk R3c BFO to the homogeneous canted spin state in a constrained epitaxial film. These studies will help us comprehensively understand the ME coupling mechanisms in the R3c BFO and shed light on design of BFO-based materials with improved multiferroic properties.

Theoretical Analysis

Improper Polarization and Invariant caused by the Reverse DM Interaction

As mentioned previously, the R3c BFO is represented by a pseudo-cubic unit cell with its proper polarization along the cubic [111]_c direction (i.e., [001]_h in the hexagonal setting; Fig. 1). Let us define [111]_c = [001]_h as the z-direction. On the other hand, the incommensurate cycloidal spin structure with a periodicity of 620 Å suggests the appearance of a small improper polarization in the R3c BFO via the reverse Dzyloshinskii-Moriya (DM) coupling^21,22,23. The spin-density wave (SDW) associated with this incommensurate spin cycloid is characterized by the propagation vector Q along the [110]_h direction in the hexagonal setting^18,19,24,25. Let us define [110]_h as the x-direction (Fig. 1). We will first examine the magnitude of this reverse DM coupling-induced parasitic polarization which is directly linked to the spin cycloid before presenting the relevant thermodynamic potential of the bulk R3c BFO. The induced polarization (ΔP _DM ) by the reverse DM interaction is expressed by the following form:

$${\rm{\Delta }}{{\boldsymbol{P}}}_{DM}={d}_{DM}{\hat{{\boldsymbol{e}}}}_{ij}\times ({{\boldsymbol{M}}}_{{\boldsymbol{i}}}\times {{\boldsymbol{M}}}_{{\boldsymbol{j}}})$$

(1)

where ${\hat{{\boldsymbol{e}}}}_{{ij}}$ denotes a unit vector connecting the two neighboring magnetic (spin) moments, M _i and M _j , at the sites i and j, respectively. Thus, we have to evaluate the position-dependent $({{\boldsymbol{M}}}_{{\boldsymbol{i}}}\times {{\boldsymbol{M}}}_{{\boldsymbol{j}}})$ to assess ΔP _DM due to the cycloidal variation of M with the propagation vector Q along [110]_h.

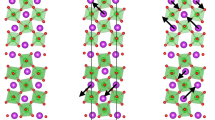
Let us call the net magnetic moment at x = 0 as M _i (i.e., the site i at x = 0). Then, M _i is given by the sum of the two neighboring canted sublattice magnetization vectors, m ₁ and m ₂ , along the z-direction (but at the same x = 0). Since the two neighboring canted magnetizations exhibit a canted antiferromagnetic (AFM) coupling along the c-axis (i.e., along [001]_h) with the canting angle $\phi$, m ₁ and m ₂ can explicitly be written as ${{\boldsymbol{m}}}_{{\boldsymbol{1}}}={{m}}_{{o}}$ $(\cos \,{\phi }\,\,\hat{{\boldsymbol{z}}}+\,\sin \,{\phi }\,\hat{{\boldsymbol{x}}})$ $+{m}_{y}\hat{{\boldsymbol{y}}}\,$  and   ${{\boldsymbol{m}}}_{{\bf{2}}}={m}_{o}(-\cos \,\phi \,\hat{{\boldsymbol{z}}}\,+\,\sin \,\phi \hat{{\boldsymbol{x}}})+{m}_{y}\hat{{\boldsymbol{y}}}$, where m _o denotes the magnitude of m ₁ (or m ₂ ) vector projected on the x-z plane (Fig. 2) and ${m}_{y}$ designates the y-component of canted spin moment with its magnitude given by m _y  = m _o sinχ = m _o sin(0.203°) = 0.0035m _o ¹⁷. Thus, M _i (≡M $(0)$) is given by

$${{\boldsymbol{M}}}_{{\boldsymbol{i}}}=2{{m}}_{{o}}\,\sin \,{\phi }\,\hat{{\boldsymbol{x}}}+2{m}_{y}\hat{{\boldsymbol{y}}}$$

(2)

On the other hand, the two neighboring canted magnetizations, m ₁ and m ₂ , at the site j, that are $\delta$ away from x = 0 are given by ${{\boldsymbol{m}}}_{1}={m}_{o}(\cos \,\phi ^{\prime} \hat{{\boldsymbol{z}}}+\,\sin \,\phi ^{\prime} \hat{{\boldsymbol{x}}})+{m}_{y}\hat{{\boldsymbol{y}}}$ and ${{\boldsymbol{m}}}_{2}={m}_{o}(-\cos \,\phi ^{\prime\prime} \hat{{\boldsymbol{z}}}+\,\sin \,\phi ^{\prime\prime} \hat{{\boldsymbol{x}}})+{m}_{y}\hat{{\boldsymbol{y}}}$, where $\phi ^{\prime} \equiv \phi +{\rm{\Delta }}\phi$ and $\phi ^{\prime\prime} \equiv \phi -{\rm{\Delta }}\phi$ with the variation of the spin-canting angle (Δφ) associated with the translation from x = 0 to x = $\delta$ along [110]_h. Thus, ${{\boldsymbol{M}}}_{{\boldsymbol{j}}}[\equiv {\boldsymbol{M}}(\delta )]$ is given by ${{\boldsymbol{M}}}_{{\boldsymbol{j}}}={m}_{o}\{\sin \phi ^{\prime} +\,\sin \,\phi ^{\prime\prime} \}\,\hat{{\boldsymbol{x}}}+{m}_{o}\{\cos \phi ^{\prime} -\,\cos \,\phi ^{\prime\prime} \}\,\hat{{\boldsymbol{z}}}+2{m}_{y}\hat{{\boldsymbol{y}}}$. This expression is readily transformed into the following form using elementary trigonometric algebra:

$${{\boldsymbol{M}}}_{{\boldsymbol{j}}}=2{m}_{o}\,\sin \,\phi \,\cos ({\rm{\Delta }}\phi )\hat{{\boldsymbol{x}}}-2{m}_{o}\,\sin \,\phi \,\sin ({\rm{\Delta }}\phi )\hat{{\boldsymbol{z}}}+2{m}_{y}\hat{{\boldsymbol{y}}}$$

(3)

Figure 2

Canted sublattice magnetization vectors and associated polarization in the R3c BFO. (a) Two sublattice magnetization vectors, m ₁ and m ₂ , at x = 0 (left-hand side) and at x = δ (right-hand side), projected on the hexagonal x-z plane. The figure shows Δφ-degree clockwise rotation of m ₁ or m ₂ , as the cycloidal spin-density wave (SDW) proceeds from x = 0 to x = δ along the [110]_h SDW propagation axis. (b) Cycloidal variation of M(x) along [110]_h. In contrast, the improper polarization caused by the reverse DM interaction, ${\rm{\Delta }}{{\boldsymbol{P}}}_{DM}$, does uniformly polarize along the z-axis and is x-location-independent. Here, the x-axis is parallel to [110]_h and the polar z-axis is parallel to [001]_h or equivalently to [111]_c. Thus, the y-axis is parallel to [$1\bar{1}0$] _h .

Plugging Eqs (2) and (3) into Eq. (1) yields the following expression for the improper polarization induced by the reverse DM coupling:

$$\begin{array}{rcl}{\rm{\Delta }}{{\boldsymbol{P}}}_{DM} & = & 4{m}_{o}^{2}{d}_{DM}{\sin }^{2}\phi \,\sin ({\rm{\Delta }}\phi )\hat{{\boldsymbol{z}}}-4{m}_{o}{m}_{y}\,\sin \,\phi \{1-\,\cos ({\rm{\Delta }}\phi )\}\hat{{\boldsymbol{y}}}\\ & = & {m}_{o}^{2}\,\sin \,\phi [4{d}_{DM}\,\sin \,\phi \,\sin \,({\rm{\Delta }}\phi )\hat{{\boldsymbol{z}}}-0.014\{1-\,\cos ({\rm{\Delta }}\phi )\}\hat{{\boldsymbol{y}}}]\\ & \approx & 4{m}_{o}^{2}{d}_{DM}\,{\sin }^{2}\phi \,\sin \,({\rm{\Delta }}\phi )\hat{{\boldsymbol{z}}}\end{array}$$

(4)

The last expression of ${{\boldsymbol{P}}}_{DM}$ is valid if $\cos ({\rm{\Delta }}\phi )\approx 1$. As defined previously, ${\rm{\Delta }}\phi$ denotes the variation of the spin-canting angle associated with the translation from one Fe-site to the nearest-neighbor Fe-site along the x-axis. Thus, Δφ = 360° $\times$ (5.58 Å/620 Å) = 3.24°, where 5.58 Å does correspond to the distance between the two nearest-neighbor Fe ions along the x-axis¹⁷. This predicts that $\cos ({\rm{\Delta }}\phi )=0.9984\approx 1$ and supports the validity of the last expression in Eq. (4). We will quantitatively examine the validity of this proposition of ignoring the y-component of the reverse DM coupling induced polarization in ‘Discussion’ section. It is interesting to notice that ${{\boldsymbol{P}}}_{DM}$ is location-independent but depends on the DM coupling strength (d _DM ), canting angle $(\phi ),$ and the periodicity of SDW through ${\rm{\Delta }}\phi$. Thus, the improper polarization induced by the reverse DM coupling does uniformly polarizes along the z-axis, i.e., along [001]_h [Fig. 2].

Within a continuum approximation for magnetic properties, the DM interaction responsible for this cycloidal modulation of spin moments in the R3c BFO can be expressed by inhomogeneous invariants, so-called ‘Lifshitz invariants’ in the free-energy density²⁶. Since the leading terms in the DM interaction are linear with respect to first spatial derivatives of magnetization in an antisymmetric mathematical form, the Lifshitz invariant for the R3c BFO can be written as

$$\begin{array}{ccc}{\rm{\Delta }}{f}_{LF} & = & {\gamma }_{s}{P}_{z}({L}_{z}\frac{{\rm{\partial }}{L}_{x}}{{\rm{\partial }}x}-{L}_{x}\frac{{\rm{\partial }}{L}_{z}}{{\rm{\partial }}x})+{\gamma {}^{{\rm{^{\prime} }}}}_{s}{P}_{x}({L}_{x}\frac{{\rm{\partial }}{L}_{z}}{{\rm{\partial }}z}-{L}_{z}\frac{{\rm{\partial }}{L}_{x}}{{\rm{\partial }}z})\\ & & +\frac{1}{2}{\kappa }_{s}\{{(\frac{{\rm{\partial }}{L}_{x}}{{\rm{\partial }}x})}^{2}+{(\frac{{\rm{\partial }}{L}_{z}}{{\rm{\partial }}x})}^{2}+{(\frac{{\rm{\partial }}{L}_{x}}{{\rm{\partial }}z})}^{2}+{(\frac{{\rm{\partial }}{L}_{z}}{{\rm{\partial }}z})}^{2}\}\end{array}$$

(5)

where ${\gamma }_{s}$ and ${\gamma ^{\prime} }_{s}$ denote the Lifshitz relativistic P-L exchange-coupling constants. Since the R3c BFO is antiferromagnetic (AFM), we used the magnitude of the AFM Néel vector, L, instead of the net magnetization order parameter, M, [$\equiv |{{\boldsymbol{m}}}_{{\bf{1}}}+{{\boldsymbol{m}}}_{{\bf{2}}}|]$, in the description of ${\rm{\Delta }}{f}_{LF}$. Herein, the DM vector is replaced by ${\gamma }_{s}P$ since the polarization couples to gradients of M or L, thereby inducing an inhomogeneous cycloidal spin configuration. In the next section, we will use this form of ${\rm{\Delta }}{f}_{LF}$ in constructing the thermodynamic potential for the R3c BFO.

Landau-Lifshitz-Ginzburg Thermodynamic Potential

Before presenting the free-energy density of the multiferroic R3c BiFeO₃ (BFO), we have first examined the free-energy density of the ferroelectric subsystem, ${\rm{\Delta }}f(P),$ on the basis of Landau-Ginzburg-Devonshire phenomenological theory^27,28,29. As mentioned previously, the R3c BFO is represented by a pseudo-cubic unit cell with its proper polarization along the cubic [111]_c direction (i.e., [001]_h in the hexagonal setting; Fig. 1). Then, the free-energy density (thermodynamic potential) of the ferroelectric subsystem can be expanded on the basis of a paraelectric prototypic cell having cubic ${P}_{m\bar{3}m}$ symmetry:

$${\rm{\Delta }}f(P)={f}_{o}+\frac{1}{2}{\chi }_{p}({P}_{x}^{2}+{P}_{y}^{2}+{P}_{z}^{2})+{\xi ^{\prime} }_{p}({P}_{x}^{4}+{P}_{y}^{4}+{P}_{z}^{4})+{\xi ^{\prime\prime} }_{p}({P}_{x}^{2}{P}_{y}^{2}+{P}_{y}^{2}{P}_{z}^{2}+{P}_{z}^{2}{P}_{x}^{2})$$

(6)

where χ _p denotes the dielectric stiffness, and ${\xi ^{\prime} }_{p},\,{\xi ^{\prime\prime} }_{p}$ are high-order stiffness coefficients. In Eq. (6), the three polarization components along the three orthogonal cubic directions are denoted by P _x ,P _y , and P _z . Then, the proper ferroelectric polarization (P) along the pseudo-cubic [111]_c is given by ${P}^{2}={P}_{x}^{2}+{P}_{y}^{2}+{P}_{z}^{2}$. Substituting this relation into Eq. (6) and suitably rearranging the resulting relation, one can obtain the following relation:

$${\rm{\Delta }}f(P)={f}_{o}+\frac{1}{2}{\chi }_{p}{P}^{2}+{\xi ^{\prime} }_{p}{P}^{4}+{\xi \prime\prime\prime }_{p}({P}_{x}^{2}{P}_{y}^{2}+{P}_{y}^{2}{P}_{z}^{2}+{P}_{z}^{2}{P}_{x}^{2})$$

(7)

where ${\xi \prime\prime\prime }_{p}$ is defined by ${\xi \prime\prime\prime }_{p}\equiv {\xi ^{\prime\prime} }_{p}-2{\xi ^{\prime} }_{p}.$ Since P is parallel to [111]_c, ${P}_{x}={P}_{y}={P}_{z}=\tfrac{1}{\sqrt{3}}P$. Substituting this relation into Eq. (7), one can immediately obtain the following expression:

$${\rm{\Delta }}f(P)={f}_{o}+\frac{1}{2}{\chi }_{p}{P}^{2}+\frac{1}{4}{\xi }_{p}{P}^{4}$$

(8)

where ξ _p is defined by ${\xi }_{p}\equiv \frac{4}{3}(3{\xi ^{\prime} }_{p}+{\xi \prime\prime\prime }_{p}) > 0.$

Considering the Lifshitz invariant for the cycloidal modulation of spin moments [Eq. (5)] and the free-energy density for the ferroelectric subsystem [Eq. (8)], one can write down the Landau-Lifshitz-Ginzburg thermodynamic potential of the single crystalline R3c BFO in terms of two independent order parameters, P and L, where L is an AFM Néel vector describing the staggered sublattice magnetization. The model free-energy density $({\rm{\Delta }}f)$ with respect to the paraphrase where $\langle P\rangle =\langle L\rangle =0$ is

$$\begin{array}{ccc}{\rm{\Delta }}f(P,\,L) & = & \frac{1}{2}{\chi }_{p}{P}^{2}+\frac{1}{4}{\xi }_{p}{P}^{4}+\frac{1}{2}{\chi }_{l}{L}^{2}+\frac{1}{4}{\xi }_{l}{L}^{4}-{\gamma }_{q}{P}^{2}({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})+\frac{1}{2}{\kappa }_{G}\sum _{i=x,y,z}({\boldsymbol{\nabla }}{L}_{i}{)}^{2}\\ & & +\,{\gamma }_{s}{P}_{z}({L}_{z}\frac{{\rm{\partial }}{L}_{x}}{{\rm{\partial }}x}-{L}_{x}\frac{{\rm{\partial }}{L}_{z}}{{\rm{\partial }}x})+{\gamma }_{s}{\rm{^{\prime} }}{P}_{x}({L}_{x}\frac{{\rm{\partial }}{L}_{z}}{{\rm{\partial }}z}-{L}_{z}\frac{{\rm{\partial }}{L}_{x}}{{\rm{\partial }}z})\\ & & +\,\frac{1}{2}{\kappa }_{s}\{{(\frac{{\rm{\partial }}{L}_{x}}{{\rm{\partial }}x})}^{2}+{(\frac{{\rm{\partial }}{L}_{z}}{{\rm{\partial }}x})}^{2}+{(\frac{{\rm{\partial }}{L}_{x}}{{\rm{\partial }}z})}^{2}+{(\frac{{\rm{\partial }}{L}_{z}}{{\rm{\partial }}z})}^{2}\}\end{array}$$

(9)

where P denotes the magnitude of the total ferroelectric polarization (proper + improper) developed along the hexagonal c-axis, i.e., [001]_h, or, equivalently, along [111]_c of the pseudo-cubic unit cell (Fig. 1)^13,14. According to our Berry-phase calculations, P ≈ P _z and P _z is as high as ~90 μC/cm² for the undoped BFO having the R3c space-group symmetry¹⁷, where P _z designates the proper off-centering polarization developed along the hexagonal [001] direction. Here, we would like to remind that ‘z’ does not refer to the cubic [001] direction. In addition, P _x  = 0 as the SDW-propagation direction (Q) is parallel to x [Fig. 3]. Equation (4) formally supports this conclusion. Several previous investigators adopted similar forms of the free-energy density in their theoretical analysis of the R3c BFO^24,30,31,32. However, the present form [Eq. (9)] is best suited to theoretical treatment of the spin-coupling-induced improper polarizations and the latent magnetization that are the two main subjects of the present study. The magnitude of the AFM Néel vector, L, is defined as L = |m ₁ − m ₂ |, where m ₁ and m ₂ denote two canted neighboring sublattice magnetization vectors²⁴. Then, it can be shown immediately that M and L are not independent of each other but are interrelated by M ² − L ² = 4(m ₁  · m ₂ ). Thus, the magnetostrictive coupling invariant in Eq. (9) can be rewritten using the following biquadratic form:

$${\rm{\Delta }}{f}_{ms}\,(\equiv {\rm{\Delta }}\,{f}_{q})=-{\gamma }_{q}{P}^{2}({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})=-\frac{1}{4}{\gamma }_{q}{P}^{2}({M}^{2}-{L}^{2}).$$

Figure 3

A two dimensional representation of the AFM Néel vector, L(x), that forms a continuously varying SDW with the propagation vector Q along the [110]_h. Herein, the improper polarization arising from the Lifshitz exchange coupling in the SDW is denoted by ${\rm{\Delta }}{{\boldsymbol{P}}}_{LF}$ and is predicted to be parallel to the z-axis or [001]_h.

Lifshitz Invariant associated with Cycloidal Spin-density Wave

As described previously, the single crystalline R3c BFO is characterized by the incommensurate SDW with the propagation vector Q along the [110]_h spiral direction in hexagonal setting^18,19,24. As schematically shown in Fig. 3, the x-location-dependent Néel vector [L(x)] forms a continuously varying cycloidal vector on the x-z plane with its propagation direction Q along $\hat{{\boldsymbol{x}}}$ (=[110]_h). Thus, the Néel vector is given by ${\boldsymbol{L}}(x)={L}_{x}\hat{{\boldsymbol{x}}}+{L}_{z}\hat{{\boldsymbol{z}}}$. Since the Néel vector L(x) lies on the x-z plane, L _y  = 0. Accordingly, we establish the following expressions for two orthogonal components of L(x):

$${L}_{x}={L}_{o}\,\sin (Qx)\,\,{\rm{a}}{\rm{n}}{\rm{d}}\,\,{L}_{z}={L}_{o}\,\cos (Qx)$$

(10)

where Q ≡ |Q| = 2π/λ with λ = 620 Å. One can readily obtain the following relations for M _x and M _z from Eq. (10): M _x  = M _o cos(Qx) and M _z  = −M _o sin(Qx). Thus, M(x) and L(x) vectors are perpendicular to each other.

Let us then find a Lifshitz invariant arising from this cycloidal SDW. One can compactly rewrite the Lifshitz invariant by assuming that ${\gamma }_{s}={\gamma }_{s}^{\prime}$ for simplicity.

$$\begin{array}{rcl}{\rm{\Delta }}{{f}}_{{LF}} & = & {{\gamma }}_{{s}}{\boldsymbol{P}}\cdot \{{\boldsymbol{L}}({\boldsymbol{\nabla }}\cdot {\boldsymbol{L}})-({\boldsymbol{L}}\cdot {\boldsymbol{\nabla }}){\boldsymbol{L}}\}+\frac{{1}}{{2}}{{k}}_{{s}}\{{({\nabla }_{{x}}{{L}}_{{x}})}^{2}+{({\nabla }_{{x}}{{L}}_{{z}})}^{2}+{({\nabla }_{{z}}{{L}}_{{x}})}^{2}+{({\nabla }_{{z}}{{L}}_{{z}})}^{2}\}\\ & \approx & {{\gamma }}_{{s}}{\boldsymbol{P}}\cdot \{{\boldsymbol{L}}({\boldsymbol{\nabla }}\cdot {\boldsymbol{L}})-({\boldsymbol{L}}\cdot {\boldsymbol{\nabla }}){\boldsymbol{L}}\}\end{array}$$

(11)

In obtaining the last expression, we omitted terms representing the square of Néel-vector gradients. According to Mostovoy³³, these nonlinear square terms do not practically contribute to the uniform improper polarization caused by the Lifshitz P-L exchange coupling. Since ${\boldsymbol{L}}(x)={L}_{x}\hat{{\boldsymbol{x}}}+{L}_{z}\hat{{\boldsymbol{z}}}$, it can be shown that the Lifshitz invariant is given by

$$\begin{array}{rcl}{\rm{\Delta }}{{f}}_{{LF}} & \approx & {{\gamma }}_{s}\{{P}_{x}\hat{{\boldsymbol{x}}}+{P}_{y}\hat{{\boldsymbol{y}}}+{P}_{z}\hat{{\boldsymbol{z}}}\}\cdot \{({L}_{x}\frac{\partial {L}_{z}}{\partial z}-{L}_{z}\frac{\partial {L}_{x}}{\partial z})\hat{{\boldsymbol{x}}}+({L}_{z}\frac{\partial {L}_{x}}{\partial x}-{L}_{x}\frac{\partial {L}_{z}}{\partial x})\hat{{\boldsymbol{z}}}\}\\ & = & {{\gamma }}_{s}{P}_{z}({L}_{z}\frac{\partial {L}_{x}}{\partial x}-{L}_{x}\frac{\partial {L}_{z}}{\partial x})\end{array}$$

(12)

In obtaining the last expression, we used the equality that $\frac{{\rm{\partial }}{L}_{z}}{{\rm{\partial }}z}=\frac{{\rm{\partial }}{L}_{x}}{{\rm{\partial }}z}=0$ since both L _x and L _z are independent of the z-coordinate [Fig. 3] and that P _x  = 0 as the SDW-propagation direction (Q) is parallel to x. Combining this result with the two relations given in Eq. (10), one can obtain the following expression of the Lifshitz invariant:

$${\rm{\Delta }}{f}_{LF}={\gamma }_{s}{P}_{z}{L}_{o}^{2\,}\{{\cos }^{2}(Qx)+{\sin }^{2}(Qx)\}Q=\,{\gamma }_{s}{P}_{z}{L}_{o}^{2\,}Q$$

(13)

where L _o (≡ L = |m ₁  − m ₂ |) denotes the magnitude of Néel vector and is given by ${L}_{o}^{2}=4{m}_{o}^{2}{\cos }^{2}\phi \approx 4{m}_{o}^{2}$ since φ ≈ 0.7° [Fig. 2].

R. de Sousa and J. E. Moore²⁴ used another form of the Lifshitz exchange coupling for the R3c BFO, which is apparently different from Δf _LF presented in Eq. (11). It is given by

$${\rm{\Delta }}{f^{\prime} }_{LF}={\gamma }_{s}{\boldsymbol{P}}\cdot \{{\boldsymbol{L}}({\boldsymbol{\nabla }}\cdot {\boldsymbol{L}})+{\boldsymbol{L}}\times ({\boldsymbol{\nabla }}\times {\boldsymbol{L}})\}$$

(14)

After carrying out several steps for mathematical rearrangements, one can show that

$${\rm{\Delta }}{f^{\prime} }_{LF}={\gamma }_{s}[\{{P}_{x}{L}_{x}(\frac{\partial {L}_{x}}{\partial x})+{P}_{x}{L}_{z}(\frac{\partial {L}_{z}}{\partial x})\}+\{{P}_{z}{L}_{z}(\frac{\partial {L}_{x}}{\partial x})-{P}_{z}{L}_{x}(\frac{\partial {L}_{z}}{\partial x})\}]$$

(15)

In obtaining the above relation, we used the equality that $(\frac{\partial {L}_{x}}{\partial y})=(\frac{\partial {L}_{x}}{\partial z})=(\frac{\partial {L}_{z}}{\partial y})=0$. As mentioned previously, P _x  = 0 since the SDW-propagation direction (Q) is parallel to x. Then, combining Eq. (15) with Eq. (10) immediately yields

$${\rm{\Delta }}{f^{\prime} }_{LF}=\,{\gamma }_{s}{P}_{z}({L}_{z}\frac{\partial {L}_{x}}{\partial x}-{L}_{x}\frac{\partial {L}_{z}}{\partial x})={\gamma }_{s}{P}_{z}{L}_{o}^{2\,}Q$$

(16)

Accordingly, ${\rm{\Delta }}{f}_{LF}={\rm{\Delta }}{f^{\prime} }_{LF}$. This indicates that the two apparently different forms of the Lifshitz invariant [i.e., Eqs (11) and (14)] are equal to each other under the condition of cycloidal spin ordering confined in an x-z plane with the translational symmetry along $\hat{{\boldsymbol{y}}}$ and the propagation direction along $\hat{{\boldsymbol{x}}}$ which is parallel to [110]_h.

Free-energy Minimization for Deducing Two Distinct Improper Polarizations

Incorporating the results of Eq. (13) for the Lifshitz invariant into Eq. (9), we obtain a simplified form of the thermodynamic potential.

$$\begin{array}{c}{\rm{\Delta }}f(P,L)=\,\frac{1}{2}{\chi }_{p}{P}^{2}+\frac{1}{4}{\xi }_{p}{P}^{4}+\frac{1}{2}{\chi }_{l}{L}^{2}+\frac{1}{4}{\xi }_{l}{L}^{4}-\frac{1}{4}{\gamma }_{q}{P}^{2}({M}^{2}-{L}^{2})\\ \quad \quad \quad \quad \quad +\frac{1}{2}{\kappa }_{G}\sum _{i=x,y,z}{({\boldsymbol{\nabla }}{L}_{i})}^{2}+{\gamma }_{s}P{L}^{2}Q\end{array}$$

(17)

where we used the notation P for the proper off-centering polarization, P _z , since P _z ≈ P. Then, consider the free-energy functional for a finite volume, ΔF = ∫dvΔf(P,L). We impose the following equality for equilibrium: $\delta \Delta F=\int dv\{{(\frac{\partial {\rm{\Delta }}f}{\partial P})}_{L}\delta P+{(\frac{\partial {\rm{\Delta }}f}{\partial L})}_{P}\delta L\}=0$. Since the P-L cross-coupling is sufficiently weak, one can establish:

$$\int dv\,\delta P{(\frac{\partial {\rm{\Delta }}f}{\partial P})}_{L}=\,\int dv\,\delta L{(\frac{\partial {\rm{\Delta }}f}{\partial L})}_{P}=0\,$$

(18)

Let us first consider the equilibrium off-centering (proper) polarization. One can immediately establish the following equality by imposing Eq. (18) to Eq. (17):

$$\int dv\,\delta P\{\,{\chi }_{p}P+{\xi }_{p}{P}^{3}-\frac{1}{2}{\gamma }_{q}({M}^{2}-{L}^{2})P+{\gamma }_{s}{L}^{2}Q\}=0\,$$

(19)

If the Lifshitz-coupling term were absent, one would obtain the following relation from Eq. (19): ${P}_{o}\{{\chi }_{p}+{\xi }_{p}{P}_{o}^{2}-\frac{1}{2}{\gamma }_{q}({M}^{2}-{L}^{2})\}=0.$ Then, one immediately obtains the following expression for the equilibrium polarization (P _o ) in the absence of the Lifshitz exchange coupling:

$${P}_{o}^{2}=-(\frac{1}{{\xi }_{p}})\{{\chi }_{p}-\frac{1}{2}{\gamma }_{q}({M}^{2}-{L}^{2})\}\equiv {({P}_{eq(0)}+{\rm{\Delta }}{P}_{ms})}^{2}$$

(20)

where ${P}_{eq(0)}$ denotes the equilibrium (proper) off-centering polarization in the absence of any intrinsic ME coupling and ${\rm{\Delta }}{P}_{ms}$ ($\equiv |{\rm{\Delta }}{{\boldsymbol{P}}}_{ms}|$) represents a small improper polarization caused by the magnetostrictive exchange coupling. Thus, ${P}_{o}$ is comprised of two distinct terms, namely, ${P}_{o}={P}_{eq(0)}+{\rm{\Delta }}{P}_{ms}$. Since ${P}_{eq(0)}\gg {\rm{\Delta }}{P}_{ms},$ we establish the following relations from Eq. (20):

$${({P}_{eq(0)})}^{2}=-(\frac{{\chi }_{p}}{{\xi }_{p}})\,\,\,{\rm{a}}{\rm{n}}{\rm{d}}\,\,\,{\rm{\Delta }}{P}_{ms}=\frac{{\gamma }_{q}({M}^{2}-{L}^{2})}{4{\xi }_{p}{P}_{eq(0)}}=\frac{{\gamma }_{q}(\,{{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})}{{\xi }_{p}{P}_{eq(0)}} < 0$$

(21)

According to the Curie-Weiss law, ${\chi }_{p}=\frac{4\pi }{c}(T-{T}_{c})$, where T _c denotes the ferroelectric Curie temperature (≈1100  K for the R3c BFO)^11,34. Thus, χ _p < 0 below T _c . Let the total equilibrium polarization that satisfies Eq. (19) be P _eq . We then establish

$${P}_{eq}\equiv {P}_{o}+{\rm{\Delta }}{P}_{LF}=({P}_{eq(0)}+{\rm{\Delta }}{P}_{ms})+{\rm{\Delta }}{P}_{LF}$$

(22)

In the above equation, ${\rm{\Delta }}{P}_{LF}$ ($\equiv |{\rm{\Delta }}{{\boldsymbol{P}}}_{LF}|$) appears due to the last term in the parenthesis of Eq. (19) and thus represents a small improper polarization arising from the Lifshitz coupling.

Owing to the Lifshitz invariant, one cannot obtain a correct analytic solution of P _eq from Eq. (19). We thus treat ${\rm{\Delta }}{P}_{LF}$ as a small perturbation to P _o and obtain a reasonably accurate solution for ${\rm{\Delta }}{P}_{LF}$. Substituting Eq. (22) into Eq. (19) yields the following equality:

$$\begin{array}{l}\{{\chi }_{p}{P}_{o}+{\xi }_{p}{P}_{o}^{3}-\frac{1}{2}{\gamma }_{q}({M}^{2}-{L}^{2}){P}_{o}\}\\ +{\chi }_{p}{\rm{\Delta }}{P}_{LF}+{\xi }_{p}\{3{P}_{o}^{2}{\rm{\Delta }}{P}_{LF}+3{P}_{o}{({\rm{\Delta }}{P}_{LF})}^{2}\}\\ -\frac{1}{2}{\gamma }_{q}({M}^{2}-{L}^{2}){\rm{\Delta }}{P}_{LF}+{\gamma }_{s}{L}_{o}^{2}Q=0\end{array}$$

(23)

As discussed previously, the terms inside the first parenthesis are equal to 0. Neglecting the term containing ${({\rm{\Delta }}{P}_{LF})}^{2}$, we eventually derive the following expressions of ${\rm{\Delta }}{P}_{LF}$:

$${\rm{\Delta }}{P}_{LF}=\,\frac{-{\gamma }_{s}\,{L}_{o}^{2}\,Q}{\{-2{\chi }_{p}+{\gamma }_{q}({M}^{2}-{L}^{2})\}}=\,\frac{-{\gamma }_{s}\,{L}_{o}^{2}\,Q}{2{\xi }_{p}{P}_{o}^{2}} > 0\,$$

(24)

In obtaining the second expression of Eq. (24), we substitute Eq. (20) for ${P}_{o}^{2}.$ On the other hand, we used the following equality in obtaining the last relation:$\,\,{\chi }_{p}+{\xi }_{p}{P}_{o}^{2}-\frac{1}{2}{\gamma }_{q}({M}^{2}-{L}^{2})=0.$ This equality was previously discussed in conjunction with Eq. (19).

On the other hand, the improper polarization caused by the magnetostrictive exchange coupling (${\rm{\Delta }}{P}_{ms}$) is given in Eq. (21). Let us now rewrite ${\rm{\Delta }}{P}_{ms}$ in terms of ${L}_{o}^{2}$ to compare this with ${\rm{\Delta }}{P}_{LF}$. The term, m ₁  · m ₂ , appeared in Eq. (21) can be rewritten in terms of the AFM spin angle $\theta$ as ${{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}}\approx {m}_{o}^{2}\,\cos \,\theta =-{m}_{o}^{2}|\cos \,\theta |=-{m}_{o}^{2}|\cos (178.6^\circ )| < 0.$ In addition to this, ${P}_{o}={P}_{eq(0)}+{\rm{\Delta }}{P}_{ms}\approx {P}_{eq(0)},$ and $|{\boldsymbol{L}}|\equiv |{{\boldsymbol{m}}}_{{\bf{1}}}-{{\boldsymbol{m}}}_{{\bf{2}}}|={L}_{o}=2{m}_{o}\,\cos \,\phi =2{m}_{o}\,\cos (0.7^\circ )\approx 2{m}_{o},$ where $\theta +2\phi$ = 180° [Fig. 2(a)]. Incorporating these three results into Eq. (21), one immediately obtains

$${\rm{\Delta }}{P}_{ms}=\frac{-{\gamma }_{q}{L}_{o}^{2}|\cos \,\theta |}{4{\xi }_{p}{P}_{o}}\approx \frac{-{\gamma }_{q}{m}_{o}^{2}}{{\xi }_{p}{P}_{o}} < 0$$

(25)

The above equation demonstrates that the improper polarization caused by the magnetostrictive interaction belongs to S _i  · S _j -type scalar coupling. According to Eq. (25), $|{\rm{\Delta }}{P}_{ms}|$ is inversely proportional to P _o . In contrast, $|{\rm{\Delta }}{P}_{LF}|$ is inversely proportional to the square of P _o . Since |cos θ| ≈ 1, the ratio of these two antiparallel improper polarizations is obtained from Eqs (24) and (25), namely, $\frac{|\Delta {P}_{LF}|}{|\Delta {P}_{ms}|}=\frac{2|{\gamma }_{s}|Q}{{\gamma }_{q}{P}_{o}}=\frac{4\pi |{\gamma }_{s}|}{{\gamma }_{q}{P}_{o}\lambda }.$ Finally, the corresponding coupling invariant (${\rm{\Delta }}{f}_{ms}$) can be obtained by using the relation described previously, ${{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}}=-{m}_{o}^{2}|\cos \,\theta |$.

$$\Delta {f}_{ms}(\equiv {\rm{\Delta }}{f}_{q})=-\frac{1}{4}{\gamma }_{q}{P}^{2}({M}^{2}-{L}^{2})=-{\gamma }_{q}{P}^{2}({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})=+{\gamma }_{q}{P}^{2}{m}_{o}^{2}|\cos \,\theta |$$

(26)

where P is nearly equal to P _z or P _o . The subscript ‘q’ appeared in $\Delta {f}_{q}$ emphasizes that the magnetostrictive interaction is represented by a biquadratic coupling of the form, P ² M ² or P ² L ². According to ϕ ⁴-expansion adopted in Eq. (8) [or Eq. (17)], the Landau coefficient ξ _p should be positive. Thus, Eq. (26) tells us that the biquadratic P-M cross-coupling thermodynamically stabilizes the R3c BFO system if γ _q < 0. On the contrary, the biquadratic magnetostrictive coupling destabilizes the system with a concomitant decrease in P _o (i.e., ${\rm{\Delta }}{P}_{ms}$ < 0) if  γ _q  > 0. According to the experimental result reported by S. Lee et al.²⁵, the latter case (γ _q  > 0) is applicable to the R3c BFO. Our theoretical estimate also supports this conclusion (‘Discussion’ section).

Since ${\rm{\Delta }}{P}_{LF}$ appeared in Eq. (24) is equal to $|{\rm{\Delta }}{{\boldsymbol{P}}}_{DM}|$ that is given in Eq. (4), one can derive the following analytical expression for the reverse DM interaction coefficient (d _DM ) which is a measure of the strength of the reverse DM coupling:

$${d}_{DM}=\frac{\pi |{\gamma }_{s}|}{\lambda {\xi }_{p}\,\sin (\Delta \phi ){\tan }^{2}\phi {P}_{o}^{2}}$$

(27)

As expected, d _DM is proportional to the Lifshitz P-L exchange-coupling constant (|γ _s |) but is inversely proportional to λ (wavelength of the SDW, 620 Å along the [110]_h). To estimate d _DM , thus, one should first know γ _s , ξ _p , and P _o . We will show all the details in ‘Discussion’ section.

Ginzburg Gradient Energy and Equilibrium Magnetic Remanence

Let us examine the second relation of Eq. (18) by applying Eq. (17) to this requirement.

$$\int dv\,\delta L{(\frac{\partial {\rm{\Delta }}f}{\partial L})}_{P}=\int dv\,\delta L[{\chi }_{l}L+{\xi }_{l}{L}^{3}+\frac{1}{2}{\gamma }_{q}{P}^{2}L+2{\gamma }_{s}PQL+\frac{1}{2}{\kappa }_{G}\frac{\partial \{{\sum }_{i}{(\nabla {{\boldsymbol{L}}}_{i})}^{2}\}}{\partial L}]=0\,$$

(28)

where κ _G denotes the Ginzburg gradient-energy coefficient. The last term inside the parenthesis of Eq. (28) can be rewritten as

$$\frac{1}{2}{\kappa }_{G}\frac{{\rm{\partial }}\{{\sum }_{i}{({\boldsymbol{\nabla }}{{\boldsymbol{L}}}_{i})}^{2}\}}{{\rm{\partial }}L}=\frac{1}{2}{\kappa }_{G}\frac{{\rm{\partial }}\{{\sum }_{i}{({\boldsymbol{\nabla }}{{\boldsymbol{L}}}_{i})}^{2}\}}{{\rm{\partial }}{L}_{i}}\frac{{\rm{\partial }}{L}_{i}}{{\rm{\partial }}L}=-{\kappa }_{G}\sum _{i}{{\boldsymbol{\nabla }}}^{2}{L}_{i}{(\frac{{\rm{\partial }}{L}_{i}}{{\rm{\partial }}L})}_{{L}_{j}}$$

(29)

Then, we obtain the following type Euler-Lagrange equation from Eq. (28):

$$L\{{\chi }_{l}+{\xi }_{l}{L}^{2}+\frac{1}{2}{\gamma }_{q}{P}^{2}+2{\gamma }_{s}PQ\}-{\kappa }_{G}\sum _{i}{\nabla }^{2}{L}_{i}{(\frac{\partial {L}_{i}}{\partial L})}_{{L}_{j}}=0$$

(30)

The Ginzburg gradient term in the above equation is comprised of three distinct terms, namely,

$$-{\kappa }_{G}\sum _{i}{\nabla }^{2}{L}_{i}{(\frac{\partial {L}_{i}}{\partial L})}_{{L}_{j}}=-{\kappa }_{G}\{\,{\nabla }^{2}{L}_{x}{(\frac{\partial {L}_{x}}{\partial L})}_{{L}_{y},{L}_{z}}+{\nabla }^{2}{L}_{y}{(\frac{\partial {L}_{y}}{\partial L})}_{{L}_{x},{L}_{z}}+{\nabla }^{2}{L}_{z}{(\frac{\partial {L}_{z}}{\partial L})}_{{L}_{x},{L}_{y}}\}$$

(31)

Since ∇² L _x  = ∇ · ∇ L _x and $\frac{\partial {L}_{x}}{\partial y}=\frac{\partial {L}_{x}}{\partial z}=0$, it is not difficult to show that ∇² L _x  = −L _o Q ² sin(Qx), where L _o denotes the magnitude of the AFM Néel vector. Similarly, it can be shown readily that ∇² L _z  = ∇ · ∇ L _z  = −L _o Q ²cos(Qx). On the contrary, ∇² L _y  = ∇ · ∇ L _y = 0. In addition, it is straightforward to show ${(\frac{\partial {L}_{x}}{\partial L})}_{{L}_{y},{L}_{z}}=\frac{{L}_{o}}{{L}_{x}}=\frac{1}{\sin (Qx)}$ and ${(\frac{\partial {L}_{z}}{\partial L})}_{{L}_{x},{L}_{y}}=\frac{{L}_{o}}{{L}_{z}}=\frac{1}{\cos (Qx)}$. Putting all these results into Eq. (31) and rearranging yields to the following expression for the Ginzburg gradient term:

$$+\frac{1}{2}{\kappa }_{G}\frac{\partial \{{\sum }_{i}{(\nabla {{\boldsymbol{L}}}_{i})}^{2}\}}{\partial L}=-{\kappa }_{G}\sum _{i}{\nabla }^{2}{L}_{i}{(\frac{\partial {L}_{i}}{\partial L})}_{{L}_{j}}=+2{\kappa }_{G}{L}_{o}{Q}^{2}$$

(32)

where L = L _o . Substituting Eq. (32) into Eq. (28) yields the following expression for the equilibrium magnitude of the AFM Néel vector:

$${({L}_{eq})}^{2}={({L}_{eq(0)})}^{2}-\frac{\{\,\frac{1}{2}{\gamma }_{q}{P}^{2}+2{\gamma }_{s}PQ+2{\kappa }_{G}{Q}^{2}\,\}}{{\xi }_{l}}$$

(33)

where ${({L}_{eq(0)})}^{2}\equiv -{\chi }_{l}/{\xi }_{l}$. Thus, ${L}_{eq(0)}$ denotes the equilibrium magnitude of the Néel vector in the absence of any coupling (i.e., γ _q  = γ _s  = κ _G  = 0). Then, the equilibrium magnetic remanence (${M}_{eq}$) is related to ${L}_{eq}$ via the following relation: ${({M}_{eq})}^{2}={({L}_{eq})}^{2}+4{({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})}_{eq}$. Combining this relation with Eq. (33) yields

$${({M}_{eq})}^{2}={({M}_{eq(0)})}^{2}+4\delta {({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})}_{eq}-\frac{\{\frac{1}{2}{\gamma }_{q}{P}^{2}+2{\gamma }_{s}PQ+2{\kappa }_{G}{Q}^{2}\}}{{\xi }_{l}}$$

(34)

where $\delta {({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})}_{eq}\equiv {({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})}_{eq}-{({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})}_{eq(0)}$ and M _eq(0) denotes the equilibrium magnetic remanence in the absence of any coupling. Thus, the Lifshitz exchange coupling enhances ${M}_{eq}$ if ${\gamma }_{s} < 0$ which corresponds to thermodynamically favorable Lifshitz coupling [Eq. (13)]. According to our theoretical estimate, γ _s is indeed negative as described in ‘Discussion’ section. In contrast, the Ginzburg gradient term always suppresses M _eq as ${\kappa }_{G} > 0.$

The Ginzburg gradient energy can be computed by considering the space average of the gradient term in Eq. (17), namely, ${\rm{\Delta }}{f}_{G}=\frac{1}{2}{\kappa }_{G}\langle {\sum }_{i}{({\boldsymbol{\nabla }}{L}_{i})}^{2}\rangle$ = $\frac{1}{2}{\kappa }_{G}\langle {({\boldsymbol{\nabla }}{L}_{x})}^{2}+{({\boldsymbol{\nabla }}{L}_{y})}^{2}+{({\boldsymbol{\nabla }}{L}_{z})}^{2}\rangle$. It can be shown readily that ${({\boldsymbol{\nabla }}{L}_{x})}^{2}=({\boldsymbol{\nabla }}{L}_{x})\cdot ({\boldsymbol{\nabla }}{L}_{x})$ $=\,{L}_{o}^{2}{Q}^{2}\,{\cos }^{2}(Qx)$ and ${({\boldsymbol{\nabla }}{L}_{z})}^{2}={L}_{o}^{2}{Q}^{2}\,{\sin }^{2}(Qx).$ On the contrary, (${\boldsymbol{\nabla }}$ L _y )² = 0 since L _y  = 0. Thus, the space average of the Ginzburg gradient term is

$${\rm{\Delta }}{f}_{G}=\frac{1}{2}{\kappa }_{G}\langle \sum _{i}{({\boldsymbol{\nabla }}{L}_{i})}^{2}\rangle =\frac{1}{2}{\kappa }_{G}{L}_{o}^{2}{Q}^{2}$$

(35)

Since κ _G  > 0, the Ginzburg gradient term always increases the free-energy density.

Discussion

Estimate of the Two distinct Improper Polarizations

Having theoretically identified the two spin-coupling-induced improper polarizations in the R3c BFO (i.e., ${\rm{\Delta }}{{P}}_{ms},\,{\rm{\Delta }}{{P}}_{LF}$), we now focus on the numerical estimate of these values with the help of ab initio density-functional theory (DFT) calculations and experimental measurements. For this, let us first consider the improper polarization caused by the magnetostrictive exchange coupling, ΔP _ms . As given in Eq. (20), this induced polarization is defined by ${\rm{\Delta }}{P}_{ms}\equiv {P}_{o}-{P}_{eq(0)}$. Since P _eq(0) denotes the off-centering (normal) ferroelectric polarization along the polar z-axis or [001]_h under the imposed condition of ${\boldsymbol{M}}={{\boldsymbol{m}}}_{{\bf{1}}}+{{\boldsymbol{m}}}_{{\bf{2}}}=0$, it does correspond to the Berry-phase polarization^35,36 obtained without imposing any spin structure (i.e., paramagnetic phase). In contrast, ${P}_{o}$ represents the net off-centering ferroelectric polarization that includes the exchange coupling effect. Thus, P _o corresponds to the Berry-phase polarization computed by imposing the canted sublattice spin structure with ${{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}}={m}_{o}^{2}\,\cos \,\theta$ = ${m}_{o}^{2}\,\cos (\pi -2\phi )={m}_{o}^{2}\,\cos (178.6^\circ )$. Since ΔP _ms belongs to ${{\boldsymbol{S}}}_{i}\cdot {{\boldsymbol{S}}}_{j}$-type scalar-coupling-induced improper polarization, the computed value of P _o by the Berry-phase method should be independent of the inclusion of spin-orbit coupling effect²². Our DFT calculations predict that ${\rm{\Delta }}{P}_{ms}\equiv {P}_{o}-{P}_{eq(0)}=-20\,$ nC/cm ², which indicates ${\gamma }_{q} > 0$ according to Eq. (25).

Let us estimate the improper polarization (${\rm{\Delta }}{{P}}_{LF}$) arising from the Lifshitz gradient coupling. For this, we have to first consider the slowly varying spin reorientation with the periodicity of 620 Å along [110]_h or x-axis. The distance between the two neighboring Fe-spin sites along the [110]_h SDW propagation axis is 5.580 Å. Thus, the spin-rotation angle (Δϕ) between the two neighboring Fe sites in the x-z plane is given by Δϕ = 360° $\times$ (5.58/620) = 3.24°. We have imposed the spin-orientation structure and performed ab initio calculations by adopting a 2 × 2 × 1 supercell. The estimated ab initio value of ΔP _LF is ~15 nC/cm ². However, this computed value is substantially smaller than the experimental value of 36 nC/cm ² along [001]_h ³⁶. Considering reliability of our ab initio value, we will adopt this experimental value in the evaluation of the Lifshitz coupling constant, γ _s , in the next section. We schematically depict these two distinct improper polarizations with their directions in Fig. 4 and these can be summarized by the following ratio: −ΔP _ms :+ΔP _LF  = 20:36 = 5:9.

Figure 4

A schematic representation of the off-centering proper ferroelectric polarization, P _eq(0), and the three parasitic improper polarizations, ${\rm{\Delta }}{{\boldsymbol{P}}}_{ms},\,\,{\rm{\Delta }}{{\boldsymbol{P}}}_{LF},$ and ${\rm{\Delta }}{{\boldsymbol{P}}}_{n}$ in the R3c BFO. Among these three improper polarizations, ${\rm{\Delta }}{{\boldsymbol{P}}}_{LF}$ is parallel to P _eq(0) but ${\rm{\Delta }}{{\boldsymbol{P}}}_{ms}$ is anti-parallel to P _eq(0). In contrast, ${\rm{\Delta }}{{\boldsymbol{P}}}_{n}$ is perpendicular to P _eq(0).

Theoretical Estimate of the Three Relevant Coupling Constants

Let us first estimate the biquadratic magnetostrictive coupling constant (γ _q ) by exploiting Eq. (25). As estimated in the previous subsection, $\Delta {P}_{ms}={P}_{o}-{P}_{eq(0)}=-2.0\times {10}^{-4}$ C/m ². According to our Berry-phase calculations, P _o  = 86.3 μC/cm ² = 0.863 C/m ². To experimentally check this value, we have fabricated a highly [111]_c-oriented 400-nm-thick BFO thin film on the (111)SrRuO₃/SrTiO₃ substrate [Fig. 5]. As shown in the polarization-electric field (P-E) hysteresis loop [Fig. 6], the remanent polarization of the [001]_h-axis-grown BFO film is ~90 μC/cm ², which nearly coincides with the computed value of P _o (=86.3 μC/cm ²).

Figure 5

High-resolution theta-2theta x-ray diffraction pattern (XRD) of the BiFeO₃(BFO)/SrRuO₃/SrTiO₃(111) thin-film heterostructure obtained using pulsed laser deposition. As shown, all three layers are characterized by the [111]_c-preferential growth. The thicknees of the ferroelectric BFO layer grown along the pseudo-cubic [111]_c is ~400 nm.

Figure 6

Polarization-electric field (P−E) hysteresis loop of the preferential [111]_c-oriented BFO film (400-nm-thick) obtained at a measuring frequency of 1 kHz at 300 K. As shown, the net switching polarization (2P _r ) of the [111]_c-preferentially grown BFO film is ~180 μC/cm ², which indicates that the remanent polarization (P _r ) is ~90 μC/cm ². According to the XRD pattern (Fig. 5), the in-plane film strain in the [111]_c-oriented BFO layer is fully relaxed at the thickness of 400 nm. Thus, the measured P _r value (~90 μC/cm ²) can be treated as a bulk P _r value of the R3c BFO.

As can be deduced from Eq. (17), the invariant for the ferroelectric subsystem is given by ${\rm{\Delta }}{f}_{p}=\frac{1}{2}{\chi }_{p}{P}^{2}+\frac{1}{4}{\xi }_{p}{P}^{4}$ − ${\gamma }_{q}{P}^{2}({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})\approx \frac{1}{2}{\chi }_{p}{P}^{2}+\frac{1}{4}{\xi }_{p}{P}^{4}$ since the biquadratic exchange coupling contribution is negligibly small as compared with the preceding two terms. From this relation, the Landau ϕ ⁴-expansion coefficient ξ _p can be derived in terms of P _eq and ${({\rm{\Delta }}{f}_{p})}_{eq},$ where ${({\rm{\Delta }}{f}_{p})}_{eq}$ denotes the equilibrium free-energy density of the ferroelectric subsystem with respect to that of the paraelectric reference system. This can be written explicitly as

$${\xi }_{p}=-4\,{({\rm{\Delta }}{f}_{p})}_{eq}\cdot {({P}_{eq})}^{-4}$$

(36)

where (P _eq )² = −χ _p /ξ _p . On the other hand, P _eq (=P _o ) = 0.863 C/m ². According to the ab initio calculations¹⁷, ${({\rm{\Delta }}{f}_{p})}_{eq}=-0.381\,eV$ per hexagonal cell containing six BFO formula cells (a = 5.57987 Å, c = 13.87229 Å), which is equivalent to −0.163 × 10⁺⁹ J/m ³. Plugging these two values into Eq. (36), one finds that ${\xi }_{p}=+1.175\times {10}^{+9}$ $(J\cdot {m}^{5}/{C}^{4}).\,$ On the other hand, ${m}_{o}\approx 5{\mu }_{B}=4.637\times {10}^{-23}\,(J\cdot {T}^{-1})$ for the high-spin Fe³⁺ in the R3c BiFeO₃ (ref.²). In addition, $|\cos \,\theta |=|\cos (\pi -2\phi )|=|\cos (178.6^\circ )|\approx 1$. Using all these values and rewriting Eq. (25) in terms of γ _q , we obtain

$${\gamma }_{q}=\frac{-{\xi }_{p}{P}_{o}\{{P}_{o}-{P}_{eq(o)}\}}{{m}_{o}^{2}}=+9.43\times {10}^{+49}\,(m\cdot {T}^{2}/J\cdot {C}^{2})$$

(37)

To estimate the Lifshitz exchange-coupling constant (γ _s ), we have reconsidered Eq. (24). As mentioned previously, we have adopted the experimental value of 3.6 × 10⁻⁴ (C/m ²) as ΔP _LF . In addition to this, we use the following values for the estimate of γ _s : P _o  = 0.863 (C/m ²), ${\xi }_{p}=+1.175\times {10}^{+9}(J\cdot {m}^{5}/{C}^{4}),$ Q = 2π/λ = 1.013 × 10⁺⁸ (m ⁻¹), and ${L}_{o}^{2}=4{m}_{o}^{2}\,{\cos }^{2}\phi \approx 4{m}_{o}^{2}$ with ${m}_{o}=4.637\times {10}^{-23}\,(J\cdot {T}^{-1})$. Using these five values and rewriting Eq. (24) in terms of γ _s , we obtain

$${\gamma }_{s}=\frac{-2\,{\xi }_{p}{P}_{o}^{2}{\rm{\Delta }}{P}_{LF}}{{L}_{o}^{2}\,Q}=-7.23\times {10}^{+41}({T}^{2}/J\cdot C)$$

(38)

As discussed previously, a negative sign of γ _s indicates that the cycloidal spin ordering is formed spontaneously in the unstrained R3c BFO. Let us now estimate d _DM , a measure of the reverse DM interaction, using Eq. (27). Then, plugging P _o  = 0.863 (C/m ²), ${\xi }_{p}=+1.175\times {10}^{+9}(J\cdot {m}^{5}/{C}^{4}),$ λ = 620 Å, Δφ = 3.24°, φ = 0.7°, and ${\gamma }_{s}=-7.23\times {10}^{+41}({T}^{2}/J\cdot C)$ into Eq. (27), we obtain ${d}_{DM}=+4.98\times {10}^{+44}({T}^{2}/J\cdot V\cdot {m}^{2})$.

Having estimated d _DM , we are now ready to examine our previous proposition that the y-component value of the reverse DM coupling-induced polarization [≡ΔP _DM (y) or ΔP_n] is relatively negligible as compared with the corresponding z-component value [$\equiv {\rm{\Delta }}{P}_{DM}(z)$] (See, the previous section of ‘Improper Polarization and Invariant caused by the Reverse DM Interaction’). According to Eq. (4), the ratio of the two perpendicular improper polarizations can be written as

$$\frac{{\rm{\Delta }}{P}_{DM}(y)}{{\rm{\Delta }}{P}_{DM}(z)}=\frac{{m}_{y}\{1-\,\cos ({\rm{\Delta }}\phi )\}}{{m}_{o}{d}_{DM}\,\sin \,\phi \,\sin ({\rm{\Delta }}\phi )}$$

(39)

We used the following values to estimate the above ratio: Δφ = 3.24°, φ = 0.7°, d _DM  = +4.98 × 10⁺⁴⁴ (T ²/J · V · m ²), and $({m}_{y}/{m}_{o})=\,\sin (\chi )$, where χ denotes the y-component spin-canting angle along the x-axis. In contrast, φ designates the x-component spin-canting angle along the z-axis [Fig. 2]. According to our previous ab initio calculations¹⁷, χ = 0.203° along the x-axis, [110]_h. Plugging all these values into Eq. (39), one obtains that ΔP _DM (y)/ΔP _DM (z) is as small as 1.65 × 10⁻⁴⁷. This clearly justifies our previous proposition that the y-component value of the reverse DM coupling-induced polarization is completely negligible as compared with the corresponding z-component value.

Release of the Latent Magnetization in a Constrained Thin Film

According to the study of Bai and co-workers³⁷, the epitaxial film-constraint induces the destruction of a spatially modulated cycloidal spin structure in the bulk R3c BFO, releasing a latent AFM component locked within the cycloid. This corresponds to a transition from the incommensurately modulated cycloidal spin state to the homogeneously canted spin state in a constrained film with the onset thickness of ~150 nm³⁸. Ryu and co-workers³⁸ further showed that the release of a latent AFM magnetization associated with the transition to the homogeneous spin state accompanies with a pronounced increase in the magnetic susceptibility (${\chi }_{m}$) in epitaxially constrained BFO thin films. We will quantitatively account for these observations by using Eq. (34). For an epitaxially constrained thin film having a homogeneous spin structure, we impose that ${\gamma }_{s}=0$ and κ _G  = 0 by considering the disappearance of a spatially modulated cycloidal spin structure³⁹. For a constrained epitaxial thin film, Eq. (34) thus reads:

$${({M}_{eq(f)})}^{2}={({M}_{eq(0)})}^{2}+4\delta {({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})}_{eq,f}-({\gamma }_{q}{P}^{2}/2{\xi }_{l}),$$

where ${M}_{eq(f)}$ denotes the equilibrium magnetic remanence of the constrained epitaxial film. On the other hand, M _eq(0) denotes the equilibrium magnetic remanence in the absence of any ME coupling. Thus, ${({M}_{eq(0)})}^{2}\equiv -{\chi }_{m}/{\xi }_{m}$. Using this relation and Eq. (34) for ${M}_{eq(b)}$, one can derive the following relation for the latent magnetization released by the transition to the homogeneously canted spin state in a constrained film:

$${\rm{\Delta }}{M}_{eq}\equiv {M}_{eq(f)}-{M}_{eq(b)}=\frac{2\{{\gamma }_{s}PQ+{\kappa }_{G}{Q}^{2}\}}{{\xi }_{l}\,\{{M}_{eq(f)}+{M}_{eq(b)}\}}\approx \frac{\{-|{\gamma }_{s}|PQ+{\kappa }_{G}{Q}^{2}\}}{{\xi }_{l}\,{M}_{eq(b)}} > 0$$

(40)

where M _eq(b) denotes the equilibrium magnetic remanence of the bulk R3c BFO and γ _s < 0. In obtaining Eq. (40) we used the following equality:

$$\begin{array}{rcl}\{4\delta {({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})}_{eq,f}-4\delta {({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})}_{eq,b}\} & = & 4\{{({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})}_{eq,f}-{({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})}_{eq,b}\}\\ & = & 4{m}_{o}^{2}\{\,\cos \,{\theta }_{f}-\,\cos \,{\theta }_{b}\}\approx 0,\end{array}$$

where the AFM spin angle of the bulk R3c BFO (θ _b ) is essentially unaffected by the formation of a constrained thin film, namely, θ _f  = θ _b  = 180° − 2φ = 178.6°. The inequality sign in Eq. (40) reflects the observation associated with the transition to the homogeneously canted spin state in a constrained epitaxial film.

One can readily obtain the following inequality by considering the right-hand-side of Eq. (40): ${k}_{G}\ge \frac{|{\gamma }_{s}|P}{Q}$. Thus, the lower limit of the Ginzburg gradient-energy coefficient [(κ _G ) _l.l.] can be estimated by using ${({k}_{G})}_{l.l.}=\frac{|{\gamma }_{s}|P}{Q}$. Plugging the previously estimated values of γ _s , P and Q into this lower limit, we obtain ${({\kappa }_{G})}_{l.l.}=6.16\times {10}^{+33}({T}^{2}/J\cdot m)$. Thus, we have estimated all four coupling constants needed for the Landau-Lifshitz-Ginzburg treatment of the R3c BFO.

The saturation magnetization (M _s ) or magnetic susceptibility (χ _M ), in general, can be readily estimated from the M-H hysteresis curve. On the contrary, ΔM _eq is too small^30,38 to quantitatively discuss this effect in terms of γ _s and κ _G . Thus, we have examined a variation in χ _M . In doing this, we first consider the thermodynamic potential of the AFM subsystem. One can write the following relation by exploiting Eq. (17) for Δf(L), Eq. (13) for the Lifshitz invariant, and Eq. (35) for the Ginzburg gradient term:

$${\rm{\Delta }}f(L)=\,+\frac{1}{2}{\chi }_{l}{L}^{2}+\frac{1}{4}{\xi }_{l}{L}^{4}-\frac{1}{4}{\gamma }_{q}{P}^{2}({M}^{2}-{L}^{2})+\frac{1}{2}{\kappa }_{G}{L}^{2}{Q}^{2}+{\gamma }_{s}P{L}^{2}Q\,\,$$

(41)

where ${L}^{2}={M}^{2}-4({{\boldsymbol{m}}}_{{\bf{1}}}\cdot {{\boldsymbol{m}}}_{{\bf{2}}})={M}^{2}-4{m}_{o}^{2}\,\cos \,\theta > {M}^{2}.$ Plugging this result into Eq. (41) and adding the term, − H · M, to Eq. (41), one can obtain the free-energy functional [Δf _H (M, θ)] under an external magnetic field, H. Taking the dynamic equilibrium condition, i.e., ${(\partial {\rm{\Delta }}{f}_{H}(M,\theta )/\partial M)}_{P,\theta }=0,$ one can eventually derive the following relation for the inverse magnetic susceptibility:

$$\frac{1}{{\chi }_{M}}\equiv {(\frac{{\rm{\partial }}H}{{\rm{\partial }}M})}_{P,\theta }=\{{\chi }_{l}+3{\xi }_{l}{M}^{2}+4{\xi }_{l}{m}_{o}^{2}|\cos \,\theta |+(2{\gamma }_{s}PQ+{\kappa }_{G}{Q}^{2})\}$$

(42)

The term inside a small bracket, 2γ _s PQ + κ _G Q ², is non-zero for a bulk crystal but is zero for a constrained epitaxial film. If this term is positive, the inverse susceptibility decreases or equivalently, M _s increases upon the transition to the homogeneous spin state in a constrained epitaxial film. On the contrary, the reverse is true if this term is negative. According to the experimental observation of χ _m ³⁸, the former is true. In other words, 2γ _s PQ + κ _G Q ² > 0, or equivalently, $|{\gamma }_{s}| < \frac{{k}_{G}Q}{2P}$.

According to Eq. (40), the enhanced magnetic remanence associated with the formation of epitaxially constrained film (ΔM _eq ) is determined by two material parameters, γ _s and κ _G . We thus have examined the effects of these two parameters on ΔM _eq as a function of the wavelength (λ) of cycloidal SDW. In doing this, we have multiplied ΔM _eq by ξ _l M _eq(b) since ΔM _eq itself is too small to be experimentally evaluated. Thus, Eq. (40) is rearranged as

$$y\equiv \{{\xi }_{l}{M}_{eq(b)}\}\cdot {\rm{\Delta }}{M}_{eq}=+{\kappa }_{G}{Q}^{2}-|{\gamma }_{s}|PQ=\frac{4{\pi }^{2}{\kappa }_{G}}{{\lambda }^{2}}-\frac{2\pi |{\gamma }_{s}|P}{\lambda }$$

(43)

Thus, y is a measure of the enhanced magnetic remanence upon the transition to the homogeneous canted spin state in a constrained thin film. As shown in Fig. 7, y decreases rapidly with increasing λ value and reaches its characteristic minimum value, which is regardless of |γ _s | or κ _G value. According to Eq. (43), y reaches its minimum at ${\lambda }_{min}=\frac{4\pi {k}_{G}}{|{\gamma }_{s}|P}$, explaining the computed result shown in Fig. 7. The characteristic minimum y value is ${y}_{min}=-\frac{|{\gamma }_{s}{|}^{2}{P}^{2}}{4{k}_{G}} < 0$. Thus, the magnitude of y _min is proportional to the square of |γ _s | but is inversely proportional to κ _G . This prediction is graphically illustrated in Fig. 7. Equation (43) further predicts that y becomes 0 at ${\lambda }_{c}=\frac{2\pi {k}_{G}}{|{\gamma }_{s}|P}$, which is regardless of |γ _s |. Thus, the critical value λ _c corresponding to (κ _G ) _l.l. (i.e., lower limit of κ _G ) can be deduced by plugging ${\kappa }_{G}=\frac{\,|{\gamma }_{s}|P}{Q}=6.16\times {10}^{+33}({T}^{2}/J\cdot m)$ into ${\lambda }_{c}=\frac{2\pi {k}_{G}}{|{\gamma }_{s}|P}$, yielding λ _c  =  620 Å. This λ _c value corresponds to the curve (ii) in Fig. 7. In case of the R3c BFO, only the region with y ≥ 0 is experimentally meaningful since the release of the latent magnetization is observed upon the transition to the homogeneously canted spin state in epitaxially constrained BFO thin films. As shown in Fig. 7, λ should be smaller than a certain critical value for ΔM _eq  > 0 (i.e., for y ≥ 0). Since ${\lambda }_{c}=\frac{2\pi {k}_{G}}{|{\gamma }_{s}|P}$, this critical λ _c value increases with κ _G but decreases with increasing value of |γ _s |.

Figure 7

Plotting the computed y value, which is a measure of ΔM _eq as a function of the wavelength (λ) of SDW. The κ _G and |γ _s | values corresponding to the three computed curves are: (i) $|{\gamma }_{s}|=7.23\times {10}^{+41}({T}^{2}/J\cdot C)$ and ${\kappa }_{G}=2{({\kappa }_{G})}_{l.l.}=12.32\times {10}^{+33}({T}^{2}/J\cdot m),$ (ii) $|{\gamma }_{s}|=7.23\times \,{10}^{+41}({T}^{2}/J\cdot C)$ and ${\kappa }_{G}={({\kappa }_{G})}_{l.l.}=$ $6.16\times {10}^{+33}({T}^{2}/J\cdot m),$ (iii) $|{\gamma ^{\prime} }_{s}|=2|{\gamma }_{s}|=14.46\times {10}^{+41}({T}^{2}/J\cdot C)$ and ${\kappa }_{G}={({\kappa }_{G})}_{l.l.}=$ $6.16\times {10}^{+33}({T}^{2}/J\cdot m)$. The same polarization (P) value of 0.863 (C/m ²) was used for all three curves. For given κ _G and |γ _s | values, there exists a certain critical value of λ below which ${\rm{\Delta }}{M}_{eq} > 0,$ or equivalently, the latent magnetization is released upon the transition to the homogeneously canted spin state in an epitaxially constrained film. The three critical λ _c values are 1240 Å, 620 Å, and 310 Å for the curve (i), (ii), and (iii), respectively.

Conclusion

We have theoretically identified the three free-energy invariants (${\rm{\Delta }}{f}_{LF},\,{\rm{\Delta }}{f}_{ms},\,{\rm{\Delta }}{f}_{G}$) that are closely related to the manifestation of the two distinct spin-coupling-induced improper polarizations by suitably exploiting the Landau-Lifshitz-Ginzburg thermodynamic potential for the R3c BFO. The two relevant parasitic improper polarizations are: (i) ${\rm{\Delta }}{{\boldsymbol{P}}}_{LF}$ arising from the Lifshitz gradient coupling, which can be equated with the improper polarization caused by the reverse DM interaction, ΔP _DM , and (ii) ΔP _ms originating from the magnetostrictive interaction. The two improper polarizations are comparable in their magnitudes (20 vs. 36 nC/cm ²). The direction of the off-centering proper ferroelectric polarization (P _eq(0)) is parallel to ΔP _LF while it is antiparallel to ΔP _ms . We have further predicted that the magnetic susceptibility (χ _m ) increases substantially upon the transition to the homogeneous spin state in a constrained epitaxial BFO film, which accounts for the experimental observation well.

Computational Methods

To obtain material parameters needed to quantitatively estimate three distinct polarizations and coupling constants, we have performed first-principles DFT calculations on the basis of the generalized gradient approximation (GGA)⁴⁰ and the GGA+U method⁴¹ implemented with the projector augmented-wave (PAW) method⁴² using the Vienna ab initio simulation package (VASP)^43,44. The Hubbard U _eff of 4.5 eV was chosen on the basis of empirical corrections. We explicitly treated five valence electrons for Bi (6s ²6p ³), eight for Fe (3d ⁶4s ²), and six for oxygen (2s ²2p ⁴). Actual DFT calculations were performed using (i) a 4 × 4 × 3 Monkhorst-Pack k-point mesh⁴⁵ centered at Γ for the R3c structure, (ii) a 500 eV plane-wave cutoff, and (iii) the tetrahedron method with the Blöchl corrections for the Brillouin-zone integrations⁴⁶. Structural optimizations were basically performed for the 30-atoms cell which corresponds to a hexagonal unit cell. In contrast, we adopted a 2 × 2 × 1 hexagonal supercell (containing 4 unit cells) to evaluate ΔP _LF .  The ions were relaxed until the Hellmann-Feynman forces on them were less than 0.01 eV/Å.