M-Polynomials and topological indices of V-Phenylenic Nanotubes and Nanotori

Abstract

V-Phenylenic nanotubes and nanotori are most comprehensively studied nanostructures due to widespread applications in the production of catalytic, gas-sensing and corrosion-resistant materials. Representing chemical compounds with M-polynomial is a recent idea and it produces nice formulas of degree-based topological indices which correlate chemical properties of the material under investigation. These indices are used in the development of quantitative structure-activity relationships (QSARs) in which the biological activity and other properties of molecules like boiling point, stability, strain energy etc. are correlated with their structures. In this paper, we determine general closed formulae for M-polynomials of V-Phylenic nanotubes and nanotori. We recover important topological degree-based indices. We also give different graphs of topological indices and their relations with the parameters of structures.

Introduction

Mathematical models, based on polynomial-representations of chemical compounds, can be used to predict their properties. Mathematical chemistry is rich in tools such as polynomials and functions which can forecast properties of compounds. Topological indices are numerical parameters of a graph which characterize its topology and are usually graph invariant. They describe the structure of molecules numerically and are used in the development of quantitative structure activity relationships (QSARs). A degree-based topological index is one sub-class where index is computed on the basis of degrees of molecular graph. These numerical values correlate structural facts and chemical reactivity, biological activities and physical properties^1,2,3,4,5. Experiments and results revealed that material properties such as boiling point, strain energy, heats of formation and reaction, viscosity, radius of gyration, and fracture toughness of a molecule are tightly connected to its structure and this fact plays a dominant role in chemical graph theory^{1, 3, 6,7,8}.

Usually topological indices are computed using definitions^{9,10,11,12,13,14,15}. One wishes to find a compact general method that can produce many topological indices of a certain category^{16, 17}. One well-established method is the computation of a general polynomial whose derivatives or integrals or blend of both, evaluated at some particular point yield topological indices. For example, Hosoya polynomial (also called Wiener polynomial), is a general polynomial whose derivatives evaluated at 1 produce Weiner and Hyper Weiner indices¹⁶. This polynomial is considered to be the most general polynomial in the context of determination of distance-based topological indices. Thus computations of distance-based topological indices reduce to computation of one single polynomial.

The M-polynomial plays parallel role in the context of degree-based topological indices and give closed formulas of more than ten degree-based topological indices^{17,18,19,20,21,22}. It is the most general polynomial developed up till now. This, in particular, implies that knowing the M-polynomial of a given family of graphs, a closed formula for any such index can be obtained routinely. Moreover, we hope that a deeper analysis of the properties of the M-polynomial will open up new general insights in the study of degree-based topological indices. Although there are other polynomials like Zagreb polynomials and Forgotten polynomial but these polynomials only give one or two degree-based topological indices (for details see^{23, 24}).

Rapid advancements are being made in this field on day to day basis. In this report, we intend to compute the M-Polynomials and Topological indices of V-Phenylenic nanotubes and nanotori. The structures of V-Phenylenic nanotubes and nanotorus consist of several C ₄ C ₆ C ₈ nets. A C ₄ C ₆ C ₈ net is a trivalent decoration made by alternate C ₄ , C ₆ , and C ₈ . Phenylenes are polycyclic conjugated molecules, composed of four-membered and six-membered rings such that every four-membered ring is adjacent to two six-membered rings and a four-membered ring is adjacent to two eight-membered rings. We denote the V-Phenylenic nanotubes and nanotorus by VPHX[m, n], and VPHY[m, n] respectively, where m and n are the number of atoms in rows and columns. In ⁹, authors computed Pi polynomial and related topological indices of V-Phenylenic nanotubes and nanotori and in¹⁰ computed general forms of theta polynomial and theta index of these materials. Many well-known topological indices of these materials have been recently computed. For example, authors computed vertex Pi index in¹¹, GA and atom-bond connectivity index in¹², eccentricity connectivity index in¹³, GA ₅ index in¹⁴ and fourth atom-bond connectivity index in¹⁵.

All graphs in this report are connected and simple. For the rest of this article we reserve V(G) as set of vertices, E(G) as the set of edges and d _v as the degree of a vertex v.

Definition 1. The M-polynomial associated to a graph G denoted as M (G, x, y) is¹⁷

$$M(G,x,y)=\sum _{\delta \le i\le j\le {\rm{\Delta }}}{m}_{ij}(G){x}^{i}{y}^{j},$$

(1)

where δ = Min{d _v |v ∈ V (G)},Δ = Max{d _v |v ∈ V (G)}, and m _ij (G) is the edge vu ∈ E(G) such that {d _v , d _u } = {i, j}.

Example: Let we have a graph G shown in Fig. 1 for which |E(G)| = 24 and |V(G)| = 17. It is easy to see that the set of vertices of G can be divided into two parts with respect to degree of the vertices, i.e. V ₁(G) = {v ∈ V(G): d _v  = 2} and V ₂(G) = {v ∈ V(G): d _v  = 16} such that |V ₁(G)| = 16 and |V ₂(G)| = 1. The set of edges of G also has two partitions, i.e. E ₁(G) = {uv ∈ E(G): d _u  = d _v  = 2} and E ₂(G) = {uv ∈ E(G): d _u  = 2 and d _v  = 16} such that |E ₁(G)| = 8 and |E ₂(G)| = 16. Also we can observe that δ = 2 and Δ = 16.

Figure 1

Graph G.

Hence by (1) we get

$$\begin{array}{rcl}M(G;x,y) & = & \sum _{2\le i\le j\le 16}\,{m}_{ij}{x}^{i}{y}^{j}\\ & = & \sum _{2\le 2}{m}_{22}{x}^{2}{y}^{2}+\sum _{2\le 16}{m}_{216}{x}^{2}{y}^{16}\\ & = & \sum _{uv\in {E}_{1}(G)}{m}_{22}{x}^{2}{y}^{2}+\sum _{uv\in {E}_{2}(G)}{m}_{216}{x}^{2}{y}^{16}\\ & = & |{E}_{1}(G)|{x}^{2}{y}^{2}+|{E}_{2}(G)|{x}^{2}{y}^{16}\\ & = & 8{x}^{2}{y}^{2}+16{x}^{2}{y}^{16}.\end{array}$$

Path number was the first distance-based topological index formulated by Wiener²⁵, now known as Wiener index. Gradually it became famous because of its various applications; see for details^{6, 26}. Later Milan Randić in 1975, introduced Randić index²⁷, R _−1/2(G), given by

$${R}_{-1/2}(G)=\sum _{uv\in E(G)}\frac{1}{\sqrt{{d}_{u}{d}_{v}}}.$$

(2)

The generalized Randić index was proposed independently by Bollobas et al.²⁸ and Amic et al.²⁹ in 1998 and has been studied extensively by both chemist and mathematicians³⁰. A detailed survey is given in ref. 31.

The general version of Randić index is

$${R}_{\alpha }(G)=\sum _{uv\in E(G)}\frac{1}{{({d}_{u}{d}_{v})}^{\alpha }},$$

(3)

and the inverse Randić index is defined as $R{R}_{\alpha }(G)=\sum _{uv\in E(G)}{({d}_{u}{d}_{v})}^{\alpha }$.

Obviously for $\alpha =-\frac{1}{2}$ in (3), we obtain R _−1/2(G) as its particular case.

The Randić index has lots of applications in many diverse areas^{32,33,34,35,36,37,38} including drug designs. There are many reasonable arguments about the physical usage of such a simple graph invariant, but the actual fact is still a mystery.

First and second Zagreb indices^{23, 24, 39}, were introduced by Gutman and Trinajstić defined as: ${M}_{1}(G)=$ $\sum _{uv\in E(G)}({d}_{u}+{d}_{v})$ and ${M}_{2}(G)=\sum _{uv\in E(G)}({d}_{u}\times {d}_{v})$ respectively whereas second modified Zagreb index is:

$${}^{m}M_{2}(G)=\sum _{uv\in E(G)}\frac{1}{{d}_{u}{d}_{v}}.$$

(4)

The Symmetric division index which determines surface area of polychlorobiphenyls is defined as:

$${\rm{S}}{\rm{D}}{\rm{D}}({\rm{G}})=\sum _{uv\in E(G)}\{\frac{min({d}_{u},{d}_{v})}{max({d}_{u},{d}_{v})}+\frac{max({d}_{u},{d}_{v})}{min({d}_{u},{d}_{v})}\}.$$

(5)

The other version of Randic index is harmonic index defined as:

$$H(G)=\sum _{vu\in E(G)}\frac{2}{{d}_{u}+{d}_{v}}.$$

(6)

I(G), Inverse sum-index, is

$$I(G)=\sum _{vu\in E(G)}\frac{{d}_{u}{d}_{v}}{{d}_{u}+{d}_{v}}.$$

(7)

A(G), augmented Zagreb index, is

$$A(G)=\sum _{vu\in E(G)}{\{\frac{{d}_{u}{d}_{v}}{{d}_{u}+{d}_{v}-2}\}}^{3}.$$

(8)

This index gives best approximation of heat of formation of alkanes^{40, 41}. Let M(G; x, y) = f(x, y) then the following Table 1 relates above described topological indices with M-polynomial¹⁷.Where

$$\begin{array}{ccc}{Q}_{\alpha }(f(x,y)) & = & {x}^{\alpha }f(x,y),\quad {D}_{x}=x\frac{{\rm{\partial }}(f(x,y))}{{\rm{\partial }}x},\\ {D}_{y} & = & \,y\frac{{\rm{\partial }}(f(x,y))}{{\rm{\partial }}y},\quad {S}_{x}={\int }_{0}^{x}\frac{f(t,y)}{t}dt,\\ {S}_{y} & = & {\int }_{0}^{y}\frac{f(x,t)}{t}dt,\quad J(f(x,y))=f(x,x).\,\end{array}$$

Table 1 Relations of topological indices with M-polynomial.

Main Results

Here we present our main results, starting with the general closed forms of M-polynomials of V-Phenylenic nanotubes VPHX[m, n] with m and n taking only positive integral value. Then we compute M-polynomial of V-Phenylenic nanotori VPHY[m, n]. In the end, we rapidly compute many topological indices from the derived M-polynomials. We also give 3-D Plots of these polynomials using Maple 13 developed by Maplesoft. For convenience, we place V-Phenylenic nanotubes VPHX[m, n] and V-Phenylenic nanotori VPHY[m, n] into two different sections. For the rest of this article, we take m and n to be positive integers.

Computational aspects of V-Phynelenic nanotubes

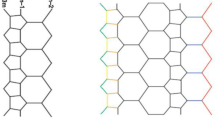
Let G=VPHX[m, n] be the V-Phenylenic nanotubes. From Fig. 2, we see that the graph has 6mn number of vertices and 9mn number of edges. The vertex partition and edge partition of graph G are shown in Tables 1 and 2 respectively.

Figure 2

2-D Lattice molecular graph of V-Phynelenic nanotube VPHX[m, n].

Table 2 The partition of V(G) of G = VPHX[m, n].

Theorem 1: Let VPHX[m, n] is the V-Phenylenic nanotubes then

$$M(VPHX[m,n];x,y)=4m{x}^{2}{y}^{3}+m(9n-5){x}^{3}{y}^{3}.$$

(9)

Proof: Let VPHX[m, n] is V-Phenylenic nanotubes, where m and n are the numbers of atoms in each row and column respectively. It is easy to see from Fig. 2 that

$$|V(VPHX[m,n])|=6mn,$$

(10)

$$|E(VPHX[m,n])|=9\,mn\mbox{--}m.$$

(11)

From Table 2, the vertex set of VPHX[m, n] have two partitions:

$${V}_{1}(VPHX[m,n])=\{u\in V(VPHX[m,n]):{d}_{u}=2\},$$

(12)

$${V}_{2}(VPHX[m,n])=\{u\in V(VPHX[m,n]):{d}_{u}=3\}$$

(13)

such that

$$|{V}_{1}(VPHX[m,n])|=2m,$$

(14)

$$|{V}_{2}(VPHX[m,n])|=6mn-2m.$$

(15)

From Table 3, the edge set of VPHX[m, n] have two partitions:

$${E}_{1}(VPHX[m,n])=\{e=uv\in E(VPHX[m,n]):{d}_{u}=2,{d}_{v}=3\},$$

(16)

$${E}_{2}(VPHX[m,n])=\{e=uv\in E(VPHX[m,n]):{d}_{u}={d}_{v}=3\}.$$

(17)

Table 3 Edge partition of edge sets of G = VPHX[m, n].

In Fig. 2 yellow labeled edges correspond to E ₁ and back labeled edges correspond to E ₂.

$$|{E}_{1}(VPHX[m,n])|=4m,$$

(18)

$$|{E}_{2}(VPHX[m,n])|=|E(VPHX[m,n])|-4m=9mn-m-4m=m(9n-5).$$

(19)

Now from the definition of the M-polynomial

$$\begin{array}{rcl}M(VPHX[m,n];x,y) & = & \sum _{i\le j}{m}_{ij}{x}^{i}{y}^{j}\\ & = & \sum _{2\le 3}{m}_{23}{x}^{2}{y}^{3}+\sum _{3\le 3}{m}_{33}{x}^{3}{y}^{3}\\ & = & \sum _{uv\in {E}_{1}(VPHX[m,n])}{m}_{23}{x}^{2}{y}^{3}+\sum _{uv\in {E}_{2}(VPHX[m,n])}{m}_{33}{x}^{3}{y}^{3}\\ & = & |{E}_{1}(VPHX[m,n])|{x}^{2}{y}^{3}+|{E}_{2}(VPHX[m,n])|{x}^{3}{y}^{3}\\ & = & 4m{x}^{2}{y}^{3}+m(9n-5){x}^{3}{y}^{3}.\end{array}$$

(20)

Above Fig. 3 is plotted using Maple 13. This suggests that values obtained by M-polynomial show different behaviors corresponding to different parameters x and y. We can control values of M-polynomial through these parameters. Clearly, Fig. 2 shows that along one side intercept is an upward opening parabola and along the other side is the downward parabola.

Figure 3

The plot of the M-polynomial of V-Phynelenic nanotube VPHX[1, 1].

Following proposition computes topological indices of V-Phenylenic nanotubes.

Proposition 2. Let VPHX[m, n] is the V-Phenylenic nanotubes.

• 1. M ₁(VPHX[m, n]) = 20m + 6m(9n − 5).

• 2. M ₂(VPHX[m, n]) = 24m + 9m(9n − 5).

• 3. ${}^{m}M_{2}(VPHX[m,n])=\frac{2}{3}m+\frac{1}{9}m(9n-5).$

• 4. R _α (VPHX[m, n]) = 2^α+ ²3^α m + 3^2α m(9n − 5).

• 5. $R{R}_{\alpha }(VPHX[m,n])=\frac{m}{{2}^{\alpha -2}{3}^{\alpha }}+\frac{m(9n-5)}{{3}^{2\alpha }}.$

• 6. $SSD(VPHX[m,n])=\frac{26}{3}m+2m(9n-5).$

• 7. $H(VPHX[m,n])=\frac{4}{5}m+\frac{1}{6}m(9n-5).$

• 8. $I(VPHX[m,n])=\frac{24}{5}m+\frac{3}{2}m(9n-5){\rm{.}}$

• 9. $A(VPHX[m,n])=32m+\frac{729}{64}m(9n-5).$

Proof.

Let

$$M(VPHX[m,n];x,y)=f(x,y)=4m{x}^{2}{y}^{3}+m(9n-5){x}^{3}{y}^{3}.$$

(21)

Then

$${D}_{x}(f(x,y))=8m{x}^{2}{y}^{3}+3m(9n-5){x}^{3}{y}^{3},$$

(22)

$${D}_{y}(f(x,y))=12m{x}^{2}{y}^{3}+3m(9n-5){x}^{3}{y}^{3},$$

(23)

$$({D}_{y}{D}_{x})(f(x,y))=24m{x}^{2}{y}^{3}+9m(9n-5){x}^{3}{y}^{3},$$

(24)

$${S}_{x}{S}_{y}(f(x,y))=\frac{2}{3}m{x}^{2}{y}^{3}+\frac{1}{9}m(9n-5){x}^{3}{y}^{3},$$

(25)

$${{D}_{x}}^{\alpha }{{D}_{y}}^{\alpha }(f(x,y))={2}^{\alpha +2}\times {3}^{\alpha }m{x}^{2}{y}^{3}+{3}^{2\alpha }m(9n-5){x}^{3}{y}^{3},$$

(26)

$${{S}_{x}}^{\alpha }{{S}_{y}}^{\alpha }(f(x,y))=\frac{1}{{2}^{\alpha -2}{3}^{\alpha }}m{x}^{2}{y}^{3}+\frac{1}{{3}^{2\alpha }}m(9n-5){x}^{3}{y}^{3},$$

(27)

$${S}_{y}{D}_{x}(f(x,y))=\frac{8}{3}m{x}^{2}{y}^{3}+m(9n-5){x}^{3}{y}^{3},$$

(28)

$${S}_{x}{D}_{y}(f(x,y))=6m{x}^{2}{y}^{3}+m(9n-5){x}^{3}{y}^{3},$$

(29)

$${S}_{x}Jf(x,y)=\frac{4}{5}m{x}^{5}+\frac{1}{6}m(9n-5){x}^{6},$$

(30)

$${S}_{x}J{D}_{x}{D}_{y}(f(x,y))=\frac{24}{5}m{x}^{5}+\frac{3}{2}m(9n-5){x}^{6},$$

(31)

$${{S}_{x}}^{3}{Q}_{-2}J{{D}_{x}}^{3}{{D}_{y}}^{3}f(x,y)={2}^{5}m{x}^{3}+\frac{{3}^{6}}{{4}^{3}}m(9n-5){x}^{4}.$$

(32)

Now from Table 1

• 1. ${M}_{1}(VPHX[m,n])={({D}_{x}+{D}_{y})(f(x,y))|}_{x=y=1}=20m+6m(9n-5).$

• 2. ${M}_{2}(VPHX[m,n])={{D}_{x}{D}_{y}(f(x,y))|}_{x=y=1}=24m+9m(9n-5).$

• 3. ${}^{m}M_{2}(VPHX[m,n])={{S}_{x}{S}_{y}(f(x,y))|}_{x=y=1}=\frac{2}{3}m+\frac{1}{9}m(9n-5).$

• 4. R _α (VPHX[m, n]) = 2^α+23^α m + 3^2α m(9n − 5).

• 5. $R{R}_{\alpha }(VPHX[m,n])=\frac{m}{{2}^{\alpha -2}{3}^{\alpha }}+\frac{m(9n-5)}{{3}^{2\alpha }}.$

• 6. $SSD(VPHX[m,n])={({S}_{y}{D}_{x}+{S}_{x}{D}_{y})(f(x,y))|}_{x=y=1}=\frac{26}{3}m+2m(9n-5).$

• 7. $H(VPHX[m,n])=2{S}_{x}J(f(x,y)){|}_{x=1}=\frac{4}{5}m+\frac{1}{6}m(9n-5).$

• 8. $I(VPHX[m,n])={S}_{x}J{D}_{x}{D}_{y}{(f(x,y))}_{x=1}=\frac{24}{5}m+\frac{3}{2}m(9n-5).$

• 9. $A(VPHX[m,n])={{{S}_{x}}^{3}{Q}_{-2}J{{D}_{x}}^{3}{{D}_{y}}^{3}(f(x,y))|}_{x=1}=32m+\frac{729}{64}m(9n-5).$

Computational aspects of the V-Phenylenic nanotori

Let VPHY[m, n] be the V-Phenylenic nanotori. From Fig. 4, we see that the graph has 6 mn number of vertices and 9  mn edges. The graph has no vertex partitions because every vertex in the graph has degree 3.

Figure 4

2D-lattice of V-Phenylenic nanotori VPHY[m, n].

Theorem 1: Let VPHY[m, n] is the V-Phenylenic nanotori then

$$M(VPHY[m,n];x,y)=9mn{x}^{3}{y}^{3}.$$

(33)

Proof: Let VPHY[m, n] is V-Phenylenic nanotori, where m and n are the number of atoms in each row and column respectively. It is easy to see from Fig. 4 that

$$|V(VPHY[m,n])|=6mn,$$

(34)

$$|E(VPHY[m,n])|=9mn.$$

(35)

There is only one type of vertices in the vertex set of VPHY[m, n]:

$${V}_{1}(VPHY[m,n])=\{u\in V(VPHY[m,n]):{d}_{u}=3\}$$

(36)

such that

$$|{V}_{1}(VPHY[m,n])|=6mn.$$

(37)

Also the edge set of VPHY[m, n] have only one type of edges:

$${E}_{1}(VPHY[m,n])=\{e=uv\in E(VPHY[m,n]):{d}_{u}={d}_{v}=3\}$$

(38)

such that

$$|{E}_{1}(VPHY[m,n])|=9mn.$$

(39)

Now again from (1) we have

$$\begin{array}{rcl}M(VPHY[m,n];x,y) & = & \sum _{i\le j}{m}_{ij}{x}^{i}{y}^{j}=\sum _{3\le 3}{m}_{33}{x}^{3}{y}^{3}\\ & = & \sum _{uv\in {E}_{2}(VPHY[m,n])}{m}_{33}{x}^{3}{y}^{3}\\ & = & |{E}_{2}(VPHX[m,n])|{x}^{3}{y}^{3}=9mn{x}^{3}{y}^{3}.\end{array}$$

(40)

Above Fig. 5 is plotted using Maple 13. This suggests that values obtained by M-polynomial show different behaviors corresponding to different parameters x and y. We can control these values through these parameters. Following proposition computes topological indices of V-Phenylenic nanotubes.

Figure 5

Plot of the M-polynomial of V-Phenylenic nanotori VPHY[1, 1].

Proposition 2. Let VPHY[m, n] is the V-Phenylenic nanotori. Then

• 1. M ₁(VPHY[m, n]) = 54mn.

• 2. M ₂(VPHy[m, n]) = 81mn.

• 3. ^m M ₂(VPHY[m, n]) = mn.

• 4. RR _α (VPHY[m, n]) = 3^2α+2 mn.

• 5. R _α (VPHY[m, n]) = 3^2−2α mn.

• 6. SSD(VPHY[m, n]) = 18mn.

• 7. $H(VPHY[m,n])=\frac{3}{2}mn.$

• 8. $I(VPHY[m,n])=\frac{27}{2}mn.$

• 9. $A(VPHY[m,n])=\frac{{3}^{8}}{{4}^{3}}mn.$

Conclusions and Discussions

We computed general forms of M-polynomials of V-Phenylenic nanotube and nanotori for the first time. Then we computed formulas for many degree-based topological indices with these polynomials. These indices are functions depending upon parameters of structures and are experimentally correlated with many properties. Moreover, we want to conclude that all indices are linearly related with the structural parameters m and n as the following Fig. 6 suggest. First one is the graph of augmented Zagreb index of V-Phenylenic Nanotube, $A({Z}_{n})=32m+\frac{729}{64}m(9n-5)$ with m and n as parameters. Second we see that this index rises with the rise in m and third shows the same tendency.

Figure 6

Plots of augmented Zagreb index of VPHX[m, n] 3D left, for m = 4 middle and for n = 5 right.

We conclude that all nine indices show the same behaviour.