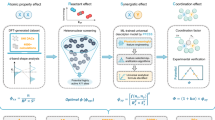
Abstract
The development of non-noble metal electrocatalysts for the Oxygen Evolution Reaction (OER) is advancing towards the use of multi-element materials. To reveal the complex correlations of multi-element OER electrocatalysts, we developed an iterative workflow combining high-throughput experiments and AI-generated content (AIGC) processes. An increased number of 909 (compared to 145 in previous literature) universal descriptors for inorganic materials science were constructed and used as Artificial Neural Network (ANN) input. A large number of statistical ensembles with each ANN individual ensemble having a reduced number of descriptors were integrated with a new Hierarchical Neural Network (HNN) algorithm. This algorithm addresses the longstanding challenge of balancing overwhelming descriptor numbers with insufficient datasets in traditional ANN approaches to materials science problems. As a result, the combination of AIGC and experimental validation significantly enhanced prediction accuracy, increase the R2 values from 0.7 to 0.98 for Tafel slopes.
Similar content being viewed by others
Introduction
The electro-catalytic oxygen evolution reaction (OER) involves the four-electron transfer. It is a rate-limiting step in water splitting and metal-air batteries1,2. Tremendous research efforts have been focused on non-noble metal OER electrocatalysts to replace the scarce and expensive noble metal catalysts (e.g., IrO2 and RuO2)3,4,5. Furthermore, multi-element materials, including ternary materials, quaternary materials and even high-entropy materials, which possess multiple active sites and associated synergistic effects have gained attention recently6,7. However, predicting the best performer among the vast compositional combinations as the number of the constituent elements increases exceeds the capability of human minds8. Hence, using artificial intelligence (AI) to build predictive models based on limited but expanding scales of data is an urgent demand from the materials research society.
Due to the improvement of computational power and statistical algorithms, AI has been employed in various scientific fields9,10,11. Xu et al. asserted that the integration of AI approaches in the materials genome Initiative (MGI) is instrumental to empower the forthcoming generation of materials scientists and facilitating a fundamental paradigm shift in materials research12. The accuracy of an AI model is highly dependent on the quantity and quality of data13,14,15. Datasets should also obey the “Findable, Accessible, Interoperable, and Reusable” (FAIR) principles16,17. Many public online resources contain a large amount of Density Functional Theory (DFT) results, and AI models have been trained based on DFT results instead of experimental data to predict material properties18. Especially in the study of multinary catalysts and even high-entropy alloys (HEAs) catalysts, which are characterized by their multiple and complex catalytic active sites, DFT combined with Machine Learning (ML) has proved effective in predicting the binding energies of various reaction intermediates on multiple catalytic active sites19,20,21,22. By integrating ML with first-principles calculations, researchers have identified HEAs with catalytic activities comparable to ruthenium for ammonia decomposition19 and platinum for ORR20. They have also uncovered local scaling relationships that constrain the optimization potential for multistep reactions and revealed CoMoFeNiCu alloys as stable and cost-effective HER catalysts21,22. These findings underscore the powerful role of computational methods in advancing catalyst design.
Further studies have advanced from modeling indirect parameters (e.g., binding energies) towards direct property parameters (e.g., exchange current densities, overpotentials and Tafel slopes)23,24,25. Saidi’s work introduces a novel electrochemical model that integrates computational and experimental approaches to enhance catalyst efficiency, leveraging computationally efficient hydrogen adsorption energy calculations23. Additionally, by refining Nørskov’s kinetic model for hydrogen evolution with a metal-dependent rate constant, they align theoretical predictions with experimental data and suggests further enhancements through machine learning24. Moreover, another work successfully grounds the Bell-Evans-Polanyi relation in hydrogen evolution kinetics by correlating activation energy with computed hydrogen adsorption free energy across multiple metal electrodes, thereby improving catalyst design prediction and accuracy25. Nevertheless, some material properties, such as catalytic activity indicators (overpotentials, turnover frequencies) for amorphous materials, are challenging to be calculated by DFT, but are easier to be measured experimentally. Therefore, we decided to employ reliable and systematic experimental datasets to develop AI models with better predictive capability for amorphous systems.
Although gathering experimental data from publications provides a viable solution, some concerns have been raised about “data corruption” by mining material data from previous literature26. Alexander J. Norquist et al. emphasized the importance of the inclusion of both successful and unsuccessful experiments in AI-assisted material discovery to achieve more accurate AI predictions27. One should also be cautious that a large number of experiments on OER catalysts with identical compositions exhibit significant variations due to different testing conditions, such as electrodes, electrolytes and potentials. High-throughput experimental methods provide a solution since they are capable of producing systematic datasets within a specified test condition, eliminating uncertainty and inconsistency28.
This study aims to take the combined advantages of a new Hierarchical Neural Network (HNN) algorithm-based AI model and systematic data to establish a catalytic performance predictive model for multi-element OER electrocatalysts. First of all, a total of 119 catalytic datasets were generated using high-throughput experiments under similar synthetic and testing conditions to train and test the HNN-based AI models. The model then generated Tafel slopes and onset overpotentials for a new ternary system. Further performance validation of the system by experiments was performed to improve the predictive capability of the model. The optimized model showed a predictive error of 2% and 4% for Tafel slopes and onset overpotentials, respectively, compared to the experiments.
Methods
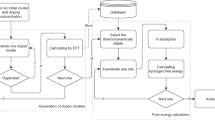
The present research employed the AI model for inorganic materials science by following these steps: (1) data collection, (2) calculating the values of descriptors (features) for each data point, (3) determining the best dimension of descriptors for each individual neural network ensemble for a given dataset, and (4) constructing HNN algorithm-based AI models. The iterative workflow of this HNN-based AI model is applicable broadly for the discovery of advanced inorganic functional materials. The evaluation metrics for the model, R2 and MAE, are detailed in Section 3 of the Supporting Information.
The collection of systematic experimental datasets
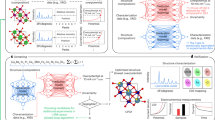
The OER electrocatalysts data was acquired using high-throughput aerogel synthesis techniques and systematic electrochemical characterization, as detailed in our previous work29,30. Multiple composition variables were accurately controlled by preparing the metal precursor solutions via a multi-channel feeding system equipped with an in-line mixer. After parallel sol to gel transition and supercritical drying, a large number of amorphous samples with different compositions were synthesized and followed by systematic Linear Sweep Voltammetry (LSV) measurements. Ternary plots of correlation between composition and electrocatalytic performance were constructed. Two composition-Tafel slopes correlation plots of FexCoyNiz and FexCoyCez electrocatalysts were obtained from high-throughput experiments with 52 data points (Fig. 4a, b). The material phases, morphologies and structures were greatly affected by the synthetic parameters (including temperature, pressure, etc.) in wet-chemical synthesis. The high-throughput synthesis ensures identical experimental conditions for all samples, i.e., the amorphous aerogels have similar morphologies and surface area to mass ratios, thereby ensuring the resultant variable electrochemical properties are primarily determined by the compositions.
Descriptor (Feature) constructions
In previous work, researchers selected a certain group of descriptors for AI models aiming at certain material properties31. In this work, we proposed to use a comprehensive and universal collection of descriptors for all different functionalities of inorganic materials. This approach will be helpful for future development of large materials AI models integrating large sets of functionalities.
Logan et al.32 pioneered the construction of universal descriptors by utilizing 22 elemental properties, which are depicted as the first 22 elemental properties in Table S1. Based on the 22 elemental properties and the statistical construction rules, a total of 145 descriptors were proposed, and then used to train and predict the formation energy and Tc of superconductors33,34,35. In this study, additional 31 elemental properties were added to sum up a total number of 53 elemental properties, as listed in Table S1. Key thermal, physical and crystallographic information was retrieved from databases (OQMD, Mathematica, ICSD and nuclear-power) or literature36,37,38. The descriptors construction rules are outlined in Table S2. A total of 901 descriptors were constructed based on the elemental properties and statistical construction rules. The configurational entropy \((\triangle {S}_{{con}})\), occupation state of valence electron and ionicity are also calculated and contributed to the other 8 descriptors to sum up to a total of 909 descriptors. Weights were allocated to the lowest, maximum, and range values according to the construction rules. It is noteworthy that \(\triangle {S}_{{con}}\) and Absolute Percentage (AP) error were added here as construction rules for descriptors due to their significant relevance in materials science. Configurational entropy serves as an indicator of the degree of disorders in the atomic distribution. The concept of AP is related to variations in atomic size and electronegativity among the different elements with a substantial impact on the material structure and properties.
The reduction of descriptor dimension for individual ANN ensemble
Due to the scarcity of experimental data in materials science, it is impossible to train all 909 descriptors using a single neural network. For example, in an Artificial Neural Network (ANN) with only two hidden layers and 909 input descriptors, more than one billion hyper-parameters would need to be determined by data training. This has posed a long-lasting challenge for an ANN AI model to solve materials science problems. A Genetic Algorithm (GA) was developed by Holland39 and frequently employed to reduce the dimension of descriptors (feature extraction) for an ANN based ML process40,41.
We used GA to reduce the dimension of descriptors for an ANN (Fig. 1) approach to the performance of electrocatalysts (including Tafel slopes and onset overpotentials). Figure 1 illustrates the progress of GA iterations on the x-axis, with the descriptor dimension (d) represented on the left y-axis and the testing R2 on the right y-axis. The descriptors reach a best dimensionality of 15 in a single ANN for the given dataset after iterative GA selection for Tafel slopes and onset overpotentials learning, with a testing R2 of 0.682 and 0.651, respectively.
Numerous ANN models, each based on different sets of reduced dimension descriptors, reached their upper limit of testing scores. The descriptors that appear most frequently during the GA iteration for Tafel slopes and onset overpotentials are shown in Table 1. Other studies have focused on identifying the most suitable set of descriptors33,34,35,36,37,38, whereas in this work the top five most frequently appearing descriptors were defined as “main descriptors”.
We found that the main descriptors screened out by the GA obey the previously reported design rationales of electrocatalysts. The electronegativity differences of various elements (MDT1) affect the charge distribution and electron cloud around the catalytic active sites, thereby affecting the adsorption and desorption kinetics of reactants42. The MDT5 and MDO3 were found to affect the work function, and correlated with the interfacial charge transfer and activity in electrocatalysts43,44. The MDO1 and MDO4 are related to the characteristics of d-electron orbitals and tuning the d-orbital electrons were found to be effective in regulating the reactant adsorption and formation of intermediate reactive species34.
Hierarchical Neural Network integrating statistical ensembles
Among these 909 descriptors, besides of five main descriptors, the remaining descriptors were classified as other descriptors. By retaining 5 main descriptors to highlight their significance and choosing additional 10 descriptors from a total pool of 909 through a randomized combinatorial algorithm, we can construct a maximum number of \({{\rm{C}}}_{904}^{10}=2.5\times {10}^{23}\) individual neural network ensembles. The selection of the optimal descriptor dimension for a specific ANN structure and dataset is carried out using GA. In conventional ML methodologies, typically only a single set of optimal descriptor combinations is chosen, disregarding alternative combinations34.
Extensive testing indicates that the various combinations of these 909 descriptors exhibit a range of performance variations from marginal declines to significant drops, but none are completely irrelevant. This observation leads us to infer that different combinations of 15 descriptors reveal distinct collective correlations between descriptors and labels (or properties). These correlations can be incrementally uncovered through training each individual neural network ensemble with 15 descriptors in parallel by the same set of data points. The full breadth of complex relationships between the 909 descriptors and various catalytic material labels is encapsulated across all individual ensembles.
To integrate the knowledge from these ensembles, a specialized statistical algorithm is necessary. Traditional algorithms, such as bagging, boosting, and stacking, often depend on straightforward geometric averaging of ensemble outputs4,35,45,46,47,48. However, owing to the variable performances across ensembles with different descriptor sets, simple geometric averaging will not effectively capture all valuable insights.
To tackle this challenge, we have devised a novel statistical integration algorithm termed ‘Hierarchical Neural Network’’ (HNN), as illustrated in Fig. 2. Each dashed box in the schematic represents an individual ensemble capable of producing one output, labeled as \({{\rm{O}}}_{{\rm{m}}}^{{\rm{i}}}\), where m and i signify the ordering of ensemble within the same layer and the layer number, respectively. Outputs from ensembles of one layer, derived from random combinations, serve as inputs (descriptors) to the next, maintaining consistent dimensionality across layers for uniformity. Outputs of each layer are inputs for the subsequent layer, supporting continuous knowledge integration and refinement. Through iterative training, appropriate weights for each neural were determined, and performance of the model progressively enhances.
The overall underlying correlation of the 909 descriptors to the key property is trained, firstly by parallel training of more than 104 such similar individual ensembles, each with a different combination of input descriptors by the same set of data points; secondly, the overall knowledge of this more than 104 statistic ensembles is then integrated and trained by the HNN algorithm. Different ensembles contain both overlapping knowledge and unique information, resulting in a superior final integrated outcome.
With a different perspective, the quantity of datasets effectively delineates the boundary conditions of the mathematical problem. With a mere 119 boundary conditions, inputting all 909 descriptors into a neural network with three hidden layers leads to an excessively high number of hyper-parameters, surpassing 9093, which compromises model training. Each individual ensemble can be likened to an individual slice in a CT scan. The hierarchical architecture of the HNN captures these correlations by cutting more than 104 slices under the same 119 boundary conditions. As the number of layers increases, the solution progressively converges to the true value. In this work, the accuracy of key properties of Tafel slopes and onset overpotentials saturate once the number of layers exceeds four, corresponding to more than thirty thousand individual ensembles.
We note that Saidi et al. introduced a ‘hierarchical convolutional neural network’’ that categorizes the data and then applied independent convolutional neural networks to each category49. Differing from that, the term “hierarchical” in this work primarily refers to the architecture of the statistical integration of large number of ensembles.
Results & discussion
The Tafel slopes and onset overpotentials, both of which are considered the key material-dependent indicator of catalytic performance, predicted by different models are shown in Fig. 3.
In Fig. 3, the numbers of 15, 145 and 909 represent the number of descriptors. Specifically, the number 15 refers to the top 15 most frequently appearing descriptors screened by GA (Fig. 2). ‘145’ is the number of universal descriptors employed in previous literature32. ‘909’ is the number of the universal descriptors proposed in this work. ANN, XGBoost and HNN indicate different AI algorithms. XGBoost50 is widely recognized as a powerful and popular machine learning algorithm, leveraging tree boosting, also known as ensemble modeling. Dataset1 contains data from FexCoyNiz (as shown in Fig. 4a) and FexCoyCez (as shown in Fig. 4b) composition-performance correlation diagram. Dataset2 contains Dataset1 and data from 30% FexCoyLaz (as shown in Fig. S3d). Dataset3 contains Dataset1 and data from 100% FexCoyLaz (as shown in Fig. 4c). Dataset4 contains Dataset3 and data of La-Co-Al, Li, K. Models trained using the 909-HNN algorithm on datasets 1-4 are named Model1T through Model4T, respectively.
The analysis uncovers several noteworthy trends: First, the performance of each model improves as the dataset size expands. We observed that with only 52 data points from two relation diagrams, the model (Model1T) showed a tendency to overfit. However, expanding the dataset to 73 samples from three relation diagrams (Model2T) significantly enhanced the prediction accuracy.
Second, the performance of 909-ANN model performance fell below that of the 15-ANN model and the 909-XGBoost. This demonstrated the contradiction between a large number of descriptors and a small number of data points existing in the traditional ANN algorithm unsolved, more descriptors will make things worse.
Third, 909-HNN outperforms all other models with different algorithms. This demonstrates that HNN algorithm effectively resolves the long-lasting contradiction between a large number of descriptors and insufficient datasets in the traditional ANN approach to materials science problems. In the following content, our study extends beyond training data evaluation by predicting and validating Tafel slope values for 15 new binary and ternary electrocatalysts. This validation step is crucial as it tests the model’s predictive power on unseen data, which is a fundamental way to check for overfitting.
The optimized AI model was further employed to predict the full composition-performance relation diagram based on experimental datasets. The final predictions and experimental comparisons of the ternary composition-Tafel-slopes correlation diagrams for Fe-Co-Ni, Fe-Co-Ce, and Fe-Co-La by Model4T are shown in Fig. 4d–f.
The predictions made by the model are commonly known as generated content (GC). One approach is to consider the GC as novel data and employ an adversarial algorithm to ensure its consistency with the original data. However, we believe that in materials science, GC should beto regarded as a prediction, and it can only be considered true and usable as data when it is experimentally validated. To illustrate the importance of the iteration of prediction and validation process, we plotted Fig. S3 & S4, and described the process in Section 4 of the supporting information.
Based on Model3T, the Tafel slope values for 15 new binary and ternary electrocatalysts were predicted and validated by experiments shown in Table 2 and Fig. S4b. Considering the feasibility of experimental synthesis for further verification and performance regulation, we selected three categories of elements from the periodic table for this research: transition metals, rare-earth metals, and alkali metals. Transition metals (training and predicted data: Fe, Co, Ni; predicted data only: Cu, Mn) are ideal non-noble metal OER catalysts due to their partially filled d-orbital electrons that effectively participate in the multi-electron transfer process. Rare earth metals (training and predicted data: La, Ce) can enhance OER catalytic activity by modulating the electronic state of transition metals through their unique 4 f electronic structure. The incorporation of alkali metals (predicted data only: Al, Li, K) may further modulate the electronic structure of transition metals, elevate the O 2p bands, and stimulate the release of lattice oxygen to enhance OER activity. Halogens are excluded from consideration due to their high electronegativity and strong ionic bonding with metals, which result in no catalytic effect on OER.
Interestingly, Model3T is able to predict the behavior of these 15 new electrocatalysts well. This is due to the fact that the model proposed here is specifically tailored for non-noble metal OER electrocatalysts, predominantly comprising transition metals and rare earth elements. In the set of 15 newly predicted electrocatalysts, each material incorporates at least one previously encountered element, such as Fe, Co, Ce, Ni, or La. For materials that include non-transition metals and rare earth elements, such as Al, Li, and K, the model’s predictive accuracy is slightly lower, with errors ranging from 2.6% to 10.8%. For example, the Tafel slope prediction error for La1Co1Al1 is 10.8%. Conversely, for materials that contain elements analogous to previously encountered transition metals, the prediction errors are lower, ranging from 0.9% to 6%. For instance, the Tafel slope prediction error for La1Co1Cu1 is 0.9%. Additionally, the Tafel slopes and onset overpotentials of these 15 new datasets also fall within the previously mentioned ranges. This suggests that the model has effectively captured the interactions between transition metals and rare earth elements in OER electrocatalysis. However, for more complex scenarios, a dataset of this limited size is insufficient for the model to achieve optimal performance.
To further improve, we added Al, Li, and K containing compounds to Dataset3 to form Dataset4. The Model4T performance shows a minor enhancement with R2 of 0.961(Fig. S4c). The difference between experiment and Model4T predictions for all 15 catalysts were shown in Fig. S4d with R2 of 0.981. As shown in Table 2, Model4T demonstrates the largest error of 5.2% for the Ce1Co1Ni1-based compounds and the smallest error of 0.01% for the La1Ni1Fe1-based compounds. These results demonstrated great predictive power with the systematic “small datasets”.
In summary, we employed a new HNN algorithm-based AI model to predict the Tafel slopes and onset overpotentials for multi-element OER electrocatalysts, yielding several noteworthy points. First, we expanded the number of universal descriptors used for ML of inorganic materials from 145 to 909. Notably, none of the five main descriptors (most frequently used) in this study were among the originally proposed set of 145 descriptors, highlighting the importance to enrich the universal descriptors. Second, we developed a HNN algorithm to integrate a large set of statistical ANN ensembles with reduced dimension of descriptors, whichresolved the contradiction between the overwhelming number of descriptors and limited scientific datasets. Third, the substantial increase in the total number of descriptors combined with the HNN algorithm led to remarkably improved prediction accuracy. Fourth, we found that even a small amount of GC datasets can significantly enhance the predictive power of AI models. However, it is crucial to validate GC through scientific experiments before it is further used. This work demonstrates the capability to accurately predict the performance of multi-element non-noble metal electrocatalysts using small, systematic datasets, thereby accelerating the path to materials innovation.
Data availability
The Tafel slopes and onset overpotentials data are provided in the supplementary file named “dataset”. The code used to generate the results in this study is available from the corresponding author upon reasonable request.
References
Chu, S. & Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 488, 294–303 (2012).
Luo, J. et al. Water photolysis at 12.3% efficiency via perovskite photovoltaics and Earth-abundant catalysts. Science 345, 1593–1596 (2014).
Calvillo, L. et al. Insights into the durability of Co–Fe spinel oxygen evolution electrocatalysts via operando studies of the catalyst structure. J. Mater. Chem. A 6, 7034–7041 (2018).
Wang, M. et al. Recent advances in transition-metal-sulfide-based bifunctional electrocatalysts for overall water splitting. J. Mater. Chem. A 9, 5320–5363 (2021).
Zhang, B. et al. Homogeneously dispersed multimetal oxygen-evolving catalysts. Science 352, 333–337 (2016).
Yao, Y. et al. High-entropy nanoparticles: Synthesis-structure-property relationships and data-driven discovery. Science 376, eabn3103 (2022). p.
Nguyen, T. X. et al. Advanced high entropy perovskite oxide electrocatalyst for oxygen evolution reaction. Adv. Funct. Mater. 31, 2101632 (2021).
Stein, H. S. et al. Functional mapping reveals mechanistic clusters for OER catalysis across (Cu–Mn–Ta–Co–Sn–Fe) O x composition and pH space. Mater. Horiz. 6, 1251–1258 (2019).
Ingraham, J. B. et al. Illuminating protein space with a programmable generative model. Nature 623, 1070–1078 (2023).
Merchant, A. et al. Scaling deep learning for materials discovery. Nature 624, 80–85 (2023).
King-Smith, E. et al. Probing the chemical ‘reactome’with high-throughput experimentation data. Nat. Chem. 1–11. (2024)
Xu, Y. et al. Artificial intelligence: A powerful paradigm for scientific research. The Innovation 2 (2021).
Gudivada, V., Apon, A. & Ding, J. Data quality considerations for big data and machine learning: going beyond data cleaning and transformations. Int. J. Adv. Softw. 10, 1–20 (2017).
Liu, Y. et al. Data quantity governance for machine learning in materials science. Natl Sci. Rev. 10, nwad125 (2023).
Jain, A. et al. Overview and importance of data quality for machine learning tasks. In Proceedings of the 26th ACM SIGKDD international conference on knowledge discovery & data mining. 2020).
Wilkinson, M. D. et al. The FAIR Guiding Principles for scientific data management and stewardship. Sci. Data 3, 1–9 (2016).
Jacobsen, A. et al. FAIR principles: interpretations and implementation considerations. Data Intell. 2, 10–29 (2020).
Wei, J. et al. Machine learning in materials science. InfoMat 1, 338–358 (2019).
Saidi, W. A., Shadid, W. & Veser, G. T. Optimization of high-entropy alloy catalyst for ammonia decomposition and ammonia synthesis. J. Phys. Chem. Lett. 12, 5185–5192 (2021).
Saidi, W. A. Optimizing the catalytic activity of Pd-based multinary alloys toward oxygen reduction reaction. J. Phys. Chem. Lett. 13, 1042–1048 (2022).
Saidi, W. A. Emergence of local scaling relations in adsorption energies on high-entropy alloys. npj Comput. Mater. 8, 86 (2022).
Saidi, W. A., Nandi, T. & Yang, T. Designing multinary noble metal‐free catalyst for hydrogen evolution reaction. Electrochem. Sci. Adv. 3, e2100224 (2023).
Yang, T. T. & Saidi, W. A. Reconciling the volcano trend with the Butler–Volmer model for the hydrogen evolution reaction. J. Phys. Chem. Lett. 13, 5310–5315 (2022).
Yang, T. T. et al. Revisiting trends in the exchange current for hydrogen evolution. Catal. Sci. Technol. 11, 6832–6838 (2021).
Yang, T. T. & Saidi, W. A. The Bell-Evans-Polanyi relation for hydrogen evolution reaction from first-principles. npj Comput. Mater. 10, 98 (2024).
Hong, W. T., Welsch, R. E. & Shao-Horn, Y. Descriptors of oxygen-evolution activity for oxides: a statistical evaluation. J. Phys. Chem. C. 120, 78–86 (2016).
Raccuglia, P. et al. Machine-learning-assisted materials discovery using failed experiments. Nature 533, 73–76 (2016).
Chen, Z. et al. Development of high‐throughput wet‐chemical synthesis techniques for material research. Mater. Genome Eng. Adv. 1, e5 (2023).
Chen, Z. et al. High-performance oxygen evolution reaction electrocatalysts discovered via high-throughput aerogel synthesis. ACS Catal. 13, 601–611 (2022).
Cai, B. et al. Developing an Fe x Co y La z-based amorphous aerogel catalyst for the oxygen evolution reaction via high throughput synthesis. J. Mater. Chem. A 12, 1793–1803 (2024).
Gheyas, I. A. & Smith, L. S. Feature subset selection in large dimensionality domains. Pattern Recognit. 43, 5–13 (2010).
Ward, L. et al. A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput. Mater. 2, 1–7 (2016).
Ward, L. et al. Including crystal structure attributes in machine learning models of formation energies via Voronoi tessellations. Phys. Rev. B 96, 024104 (2017).
Stanev, V. et al. Machine learning modeling of superconducting critical temperature. npj Comput. Mater. 4, 29 (2018).
Zhang, J. et al. An integrated machine learning model for accurate and robust prediction of superconducting critical temperature. J. Energy Chem. 78, 232–239 (2023).
Miracle, D. et al. An assessment of binary metallic glasses: correlations between structure, glass forming ability and stability. Int. Mater. Rev. 55, 218–256 (2010).
Lide, D. R. CRC handbook of chemistry and physics. Vol. 85: CRC Press (2004).
De Boer, F. R. et al. Cohesion in metals. Transition metal alloys (1988).
Holland, J. H. Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence: MIT press. (1992).
Michalewicz, Z. & Schoenauer, M. Evolutionary algorithms for constrained parameter optimization problems. Evolut. Comput. 4, 1–32 (1996).
Gu, S., Cheng, R. & Jin, Y. Feature selection for high-dimensional classification using a competitive swarm optimizer. Soft Comput. 22, 811–822 (2018).
Wang, X. et al. Electronic structure regulation of the Fe-based single-atom catalysts for oxygen electrocatalysis. Nano Energy. p. 109268 (2024).
Radinger, H. et al. Work function describes the electrocatalytic activity of graphite for vanadium oxidation. ACS Catal. 12, 6007–6015 (2022).
Qin, R. et al. Ru/Ir‐Based Electrocatalysts for Oxygen Evolution Reaction in Acidic Conditions: From Mechanisms, Optimizations to Challenges. Advanced Science. p. 2309364 (2024).
Mishra, A. et al. Ensemble-based machine learning models for phase prediction in high entropy alloys. Comput. Mater. Sci. 210, 111025 (2022).
Wang, X. et al. ThermoEPred-EL: Robust bandgap predictions of chalcogenides with diamond-like structure via feature cross-based stacked ensemble learning. Comput. Mater. Sci. 169, 109117 (2019).
Nguyen, D.-N. et al. Ensemble learning reveals dissimilarity between rare-earth transition-metal binary alloys with respect to the Curie temperature. J. Phys.: Mater. 2, 034009 (2019).
Sun, B. et al. Ensemble learning based on stacking and blending predicts glass forming ability. Mater. Today Commun. 37, 107385 (2023).
Saidi, W. A., Shadid, W. & Castelli, I. E. Machine-learning structural and electronic properties of metal halide perovskites using a hierarchical convolutional neural network. npj Comput. Mater. 6, 36 (2020).
Chen, T. & Guestrin, C. Xgboost: A scalable tree boosting system. in Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining (2016).
Acknowledgements
We acknowledge the funding support from National Key R&D Program of China (Grant No. 2022YFB3807700), Shenzhen Fundamental Research Funding (No. JCYJ20220818100612027 and JCYJ20220818100613028), National Natural Science Foundation of China (Grant No. 22309075) and the Major Science and Technology Infrastructure Project of Shenzhen Material Genome Big-Science Facilities Platform.
Author information
Authors and Affiliations
Contributions
S.M.X. developed the AI algorithms, drafted the manuscript, and created the visualizations. Z.Y.C. provided guidance on the high-throughput experimental design and edited the manuscript. M.Y.Q. contributed to the manuscript revision. B.J.C., W.X.L. and R.G.Z. conducted the high-throughput experiments and managed the data collection. C.X. performed the formal analysis, drafted sections of the manuscript, and edited the final version. X.-D.X., the principal investigator, conceptualized the research, provided overall supervision, and secured the financial support for the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Xu, S., Chen, Z., Qin, M. et al. Developing new electrocatalysts for oxygen evolution reaction via high throughput experiments and artificial intelligence. npj Comput Mater 10, 194 (2024). https://doi.org/10.1038/s41524-024-01386-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-024-01386-4