Tensor-structured algorithm for reduced-order scaling large-scale Kohn–Sham density functional theory calculations

Abstract

We present a tensor-structured algorithm for efficient large-scale density functional theory (DFT) calculations by constructing a Tucker tensor basis that is adapted to the Kohn–Sham Hamiltonian and localized in real-space. The proposed approach uses an additive separable approximation to the Kohn–Sham Hamiltonian and an L₁ localization technique to generate the 1-D localized functions that constitute the Tucker tensor basis. Numerical results show that the resulting Tucker tensor basis exhibits exponential convergence in the ground-state energy with increasing Tucker rank. Further, the proposed tensor-structured algorithm demonstrated sub-quadratic scaling with system-size for both systems with and without a gap, and involving many thousands of atoms. This reduced-order scaling has also resulted in the proposed approach outperforming plane-wave DFT implementation for systems beyond 2000 electrons.

Introduction

Density functional theory (DFT) has been the workhorse of ab-initio materials simulations for over three decades, providing many key insights into materials properties and materials behavior. In order to study ground-state properties, based on the Hohenberg–Kohn theorem¹ and the Kohn–Sham formulation², DFT reduces the Schrödinger equation in 3N_e spatial coordinates (N_e denoting the number of electrons) to an equivalent problem in the electron-density that only depends on three spatial coordinates. This reduces the exponential computational complexity (with system-size) of solving the Schrödinger equation to the cubic computational complexity of DFT. While DFT has enabled wide-ranging ab-initio calculations, with ~1/4th of the computational resources on some public supercomputers utilized for DFT calculations, the cubic computational complexity has limited routine DFT calculations to typical system-sizes involving a few hundred atoms. In an attempt to enable DFT calculations on large-scale systems that are critical to understanding many aspects of complex materials phenomena, many efforts over the past three decades have focused on developing reduced-order scaling algorithms for electronic structure calculations^{3,4,5,6,7,8,9,10,11,12,13}. These approaches have either relied on a localized representation of the single-electron wavefunctions (such as Wannier functions⁵) or the exponential decay of the density-matrix in real-space, and have been demonstrated to provide close to linear-scaling complexity for materials with a gap. However, they have not been widely successful for metallic systems (without a gap) either due to the errors resulting from realizing locality in the wavefunctions in real-space or due to the higher prefactors that make these approaches computationally more expensive than the traditional cubic-scaling algorithms for system-sizes of interest. In this work, we present an alternative direction by using tensor-structured ideas to achieve systematically convergent and efficient DFT calculations that exhibit sub-quadratic scaling for systems with and without a gap over system-sizes spanning many thousands of atoms.

This line of work is motivated from a study that revealed a low-rank representation for the electronic structure using Tucker and canonical tensor decomposition^14,15,16. Another study based on a posteriori analysis showed that the rank required to approximate the electron-density is only weakly dependent on the system-size¹⁷. These studies have thereby prompted the development of a tensor-structured approach for DFT calculations¹⁸, where a Tucker tensor basis adapted to the Kohn–sham Hamiltonian was employed to solve the Kohn–Sham equations. Importantly, the rank of the Tucker tensor basis was only weakly dependent with system-size for materials systems with and without a gap, which revealed the potential for realizing a reduced-order scaling approach for DFT calculations. However, since the constructed Tucker tensor basis is global, the representation of the Kohn–Sham Hamiltonian in this basis was dense. An L₂ localization scheme that was explored to localize the Tucker tensor basis did not provide sufficient locality to exploit sparsity in the Kohn–Sham Hamiltonian. With increasing system-size, albeit the slow growth in the size of the Hamiltonian matrix due to the weak rank dependence, the approach became computationally prohibitive for large systems and limited the system-sizes to a few hundred atoms.

In this work, L₁ localization is used to overcome the aforementioned drawbacks, and we demonstrate systematically convergent, efficient and reduced-order scaling large-scale DFT calculations using tensor-structured techniques (cf. Fig. 1 for an overview of the approach). The L₁ localization utilizes the idea of auto-encoder commonly recognized in machine learning to construct a series of 1-D functions that are localized yet closely approximate the function space of interest. The 1-D localized functions that are a close approximation to the eigensubspace of a suitably constructed additive separable approximation of the Kohn–Sham Hamiltonian are used to generate the localized Tucker tensor basis for the DFT problem. The locality of the Tucker tensor basis results in a sparse discrete Kohn–Sham Hamiltonian matrix, which is exploited in the solution of the Kohn–Sham equations using the Chebyshev filtering subspace iteration scheme. The sparsity of the Kohn–Sham Hamiltonian matrix represented in the localized Tucker tensor basis improves both the computational efficiency and the memory footprint. Further, as will be demonstrated, the proposed approach has enabled sub-quadratic scaling DFT calculations on large-scale systems involving many thousands of atoms. The approach is generic and treats both systems with and without a gap on an equal footing. Importantly, this translates to substantial speed-ups over Quantum Espresso (QE), a widely used state-of-the-art plane-wave DFT code^19,20, with speed-ups of ~8-fold for metallic nano-particles containing ~2000 atoms.

Fig. 1: Overview of the tensor-structured algorithm for Kohn–Sham DFT using L₁ localized functions.

The tensor-structured algorithm seeks to construct a systematically convergent reduced-order tensor-structured basis for efficiently solving the Kohn–Sham equations. To this end, an additive separable approximation to the Kohn–Sham Hamiltonian is constructed, whose eigenbasis presents a suitable reduced-order basis, given by ${T}_{I}={\psi }_{1,{i}_{1}}{\psi }_{2,{i}_{2}}{\psi }_{3,{i}_{3}}$, where I is a composite index I = (i₁, i₂, i₃). However, the discrete Kohn–Sham Hamiltonian in this basis is dense due to the global nature of the 1-D functions ${\psi }_{k,{i}_{k}}$, k = 1, 2, 3 (lower-left). The L₁ localization is applied to alleviate this bottleneck, where localized tensor-structured basis functions are constructed such that the subspace spanned by this localized basis is a close approximation to the eigensubspace of the separable Hamiltonian. Denoting the localized 1-D functions by ${\psi }_{k,{i}_{k}}^{{\rm{L}}}$, the 3-D localized basis functions are given by ${T}_{I}^{{\rm{L}}}={\psi }_{1,{i}_{1}}^{{\rm{L}}}{\psi }_{2,{i}_{2}}^{{\rm{L}}}{\psi }_{3,{i}_{3}}^{{\rm{L}}}$. The 3-D localized basis functions, being compactly supported, yields a sparse Hamiltonian (lower-right). The resulting sparse Hamiltonian, in conjunction with the slow growth of the Tucker rank with system-size to accurately represent the electronic structure, has provided sub-quadratic scaling with system-size for both insulating and metallic systems spanning over many thousands of atoms.

Results

The Kohn–Sham DFT formulation

The ground state energy in Kohn–Sham DFT (spin-independent formulation) of a materials system with N_a atoms and N_e electrons is computed by solving a non-interacting single-particle Schrödinger equation in a mean-field determined by the effective potential V_eff(x):

$$\left(-\frac{1}{2}{\nabla }^{2}+{V}_{{\rm{eff}}}({\bf{x}})\right){{{\Psi }}}_{i}={\epsilon }_{i}{{{\Psi }}}_{i},\quad i\in \{1,...,N\}.$$

(1)

Equation (1) represents a non-linear eigenvalue problem with ${\mathcal{H}}:= -\frac{1}{2}{\nabla }^{2}+{V}_{{\rm{eff}}}$ being the Kohn–Sham Hamiltonian, and ϵ_i denoting the ith Kohn–Sham eigenvalue and Ψ_i denoting the corresponding Kohn–Sham orbital (eigenvector). The effective potential V_eff and the subsequent Hamiltonian matrix elements can be evaluated efficiently using a low-rank Tucker tensor approximation and tensor-structured techniques (cf. Supplementary Method: Kohn–Sham effective potential computation using tensor-structured techniques). The electron-density ρ(x) is computed in terms of the Kohn–Sham eigenstates as $\rho ({\bf{x}})=2\mathop{\sum }\nolimits_{i = 1}^{N}f({\epsilon }_{i};\mu){\left|{{{\Psi }}}_{i}({\bf{x}})\right|}^{2}$, where $f({\epsilon }_{i};\mu)$ denotes the orbital occupancy factor given by the Fermi–Dirac distribution $f(\epsilon ;\mu)=1/\left(1+{\mathrm {exp}}(\frac{\epsilon\, -\,\mu }{{k}_{{\mathrm {B}}}T})\right)$ with the Boltzmann constant k_B, the Fermi energy μ, and the smearing temperature T. We note that Eq. (1) represents a non-linear eigenvalue problem, as the Kohn–Sham Hamiltonian depends on ρ, which in turn depends on the eigenstates. Thus, Eq. (1) is solved self-consistently via a self-consistent field (SCF) iteration²¹.

Tensor-structured algorithm using L ₁ localized 1-D functions

In our previous work¹⁸, it was suggested that an additive separable approximation to the Kohn–Sham Hamiltonian can be used to construct a Tucker tensor basis that is systematically convergent. In particular, using a tensor-structured cuboidal domain Ω spanned by the tensor product of 1-D domains ω_k=1,2,3, an additive separable approximation to the Kohn–Sham Hamiltonian (${{\mathcal{H}}}_{1}({x}_{1})+{{\mathcal{H}}}_{2}({x}_{2})+{{\mathcal{H}}}_{3}({x}_{3})\approx {\mathcal{H}}({\bf{x}})$) retains some features of the Hamiltonian, and thus presents a useful operator to generate reduced-order basis functions. To this end, the eigenfunctions of the additive separable approximation to the Hamiltonian, which constitute a Tucker tensor basis formed from the 1-D eigenfunctions of the separable parts of the Hamiltonian (${{\mathcal{H}}}_{k}$, k = 1, 2, 3), are used to solve the Kohn–Sham equations. While an efficient basis, the global nature of the ensuing Tucker tensor basis limits the computational efficiency of the algorithms to solve the Kohn–Sham equations. In the proposed work, in place of the 1-D eigenfunctions of ${{\mathcal{H}}}_{k}$, we instead construct compressed modes preserving the subspace spanned by the 1-D eigenfunctions using the L₁ localization technique²². The obtained 1-D localized functions are then used to generate the 3-D Tucker tensor basis, which is localized in real-space and allows us to exploit the sparsity of the Kohn–Sham Hamiltonian represented in this basis for both computational efficiency and realizing reduced-order scaling in solving the Kohn–Sham equations. The various aspects of our tensor-structured algorithm are now presented, which include the generation of the additive separable approximation of the Kohn–Sham Hamiltonian, the evaluation of the L₁ localized 1-D functions, the construction of the localized Tucker tensor basis, the projection of the Kohn–Sham problem onto the localized Tucker tensor basis, and the solution of the Kohn–Sham equations.

Construction of separable Hamiltonian

We seek to construct a separable approximation to the Kohn–Sham Hamiltonian ${{\mathcal{H}}}_{1}({x}_{1})+{{\mathcal{H}}}_{2}({x}_{2})+{{\mathcal{H}}}_{3}({x}_{3})\approx {\mathcal{H}}({\bf{x}})$ based on a rank-1 approximation of the eigenfunction corresponding to the lowest eigenvalue. To this end, we consider the rank-1 representation for the eigenfunction as ${{\Psi }}^{\prime} ({\bf{x}})={\psi }_{1}({x}_{1}){\psi }_{2}({x}_{2}){\psi }_{3}({x}_{3})$. Thus, the problem of computing the smallest eigenvalue of the Kohn–Sham Hamiltonian using the rank-1 approximation is given by the variational problem

$$\mathop{\min }\limits_{{\psi }_{k}}\ L({{\Psi }}^{\prime})\quad \quad \,{\mathrm{subject}} \, {\mathrm{to:}}\,\left\langle {{\Psi }}^{\prime} | {{\Psi }}^{\prime} \right\rangle =1$$

(2)

with the Lagrangian $L({{\Psi }}^{\prime})=\left\langle {{\Psi }}^{\prime} \right|-\frac{1}{2}{\nabla }^{2}+{V}_{{\rm{eff}}}({\bf{x}})\left|{{\Psi }}^{\prime} \right\rangle$. Upon taking the variations of the functional with respect to ψ₁, ψ₂ and ψ₃, we obtain three simultaneous 1-D problems

$${{\mathcal{H}}}_{k}{\psi }_{k}={\alpha }_{k}{\psi }_{k},\quad k=1,2,3.$$

(3)

As ${{\mathcal{H}}}_{k}$ and α_k are parametrized by ψ_l≠k, the three simultaneous 1-D problems represent a non-linear problem that can be solved self-consistently via SCF iteration (cf. Supplementary Method: Minimization problem for computing separable Hamiltonian approximation). Upon achieving self-consistency, the 1-D Hamiltonians (${{\mathcal{H}}}_{k}$) we obtain represent the additive separable approximation of the Kohn–Sham Hamiltonian that we seek. The eigenfunctions of this additive separable approximation to the Hamiltonian, which can be obtained as the tensor product of the 1-D eigenfunctions of ${{\mathcal{H}}}_{k}$ (k = 1, 2, 3), constitute a complete basis, thus providing systematic convergence as will be demonstrated subsequently.

We note that the proposed approach represents one possibility of systematically constructing an additive separable approximation to the Kohn–Sham Hamiltonian, and other possibilities may exist. We also note that the resulting tensor-structured basis—the eigenbasis of ${{\mathcal{H}}}_{1}+{{\mathcal{H}}}_{2}+{{\mathcal{H}}}_{3}$—is expected to be better than the plane-wave basis. To elaborate, the plane-wave basis is the eigenbasis of the Laplace operator (which is additive separable), whereas the additive separable approximation obtained via the proposed approach includes both the Laplace operator and an additive separable approximation of the Kohn–Sham potential V_eff, thus retaining some additional features of the Kohn–Sham Hamiltonian and providing a better basis than the plane-wave basis. The superior approximation properties of the proposed tensor-structured basis over the plane-wave basis will be demonstrated subsequently via numerical benchmark studies (cf. Tables 1 and 2).

Table 1 Comparison of the computational performance for Aluminum nano-particles.

Table 2 Comparison of the computational performance for silicon quantum dots.

We further note that the Kohn–Sham Hamiltonian changes during the course of the SCF iteration. In principle, the separable approximation to the Kohn–Sham Hamiltonian can be computed for each SCF iteration adapting the tensor-structured basis to the Hamiltonian in a given SCF iteration. However, in this work, we choose to keep the basis fixed after computing the tensor-structured basis in the first SCF iteration using the Kohn–Sham potential obtained from the superposition of atomic densities. This is motivated from our numerical studies on the benchmark examples involving both metallic and insulating systems, which demonstrate that the approximation properties of the resulting tensor-structured basis are not substantially altered. In particular, the difference in the ground-state energies obtained by either using a fixed basis constructed in the first SCF or adapting the basis in every SCF is substantially smaller than the basis discretization error. We refer to Supplementary Note 1 for data supporting this observation (cf. Supplementary Table 1).

Computation of L ₁ localized 1-D functions

The tensor-structured basis computed using the 1-D eigenfunctions of ${{\mathcal{H}}}_{k}$ represents an efficient basis. However, the global nature of the basis limits the computational efficiency and scaling (with system-size) of the solution to the Kohn–Sham equations. To this end, we use the L₁ localization approach²² to construct a spatially localized tensor-structured basis that is a close approximation to the original tensor-structured basis. The localized basis is obtained by solving the following variational problem (for k = 1, 2, 3):

$$\mathop{\min }\limits_{{{\mathbf{\Psi }}}_{k}^{\prime}\in {{\mathbb{R}}}^{n\times {N}_{k}}}\frac{1}{\mu }\left|{{\mathbf{\Psi }}}_{k}^{\prime}\right|+{\rm{Tr}}({{{\mathbf{\Psi }}}_{k}^{\prime}}^{{\mathrm {T}}}{{\mathbf{H}}}_{k}{{\mathbf{\Psi }}}_{k}^{\prime})\quad {\rm{s.t.}}\ \ {{{\mathbf{\Psi }}}_{k}^{\prime}}^{{\mathrm {T}}}{{\mathbf{\Psi }}}_{k}^{\prime}={\mathbf{I}},$$

(4)

where H_k is the matrix representation of ${{\mathcal{H}}}_{k}$ in a suitable orthogonal basis with dimension n, ${{\bf{\Psi }}}_{k}^{\prime}$ denotes the representation of N_k trial localized functions in the chosen basis, and μ is a parameter controlling the trade-off between the representability of the original eigensubspace and the locality of the 1-D functions, with $\left|\cdot \right|$ denoting the L₁ norm of the matrix. The minimizer of this variational problem, henceforth denoted as ${{\mathbf{\Psi }}}_{k}^{{\rm{L}}}$, provides localized functions whose span closely approximates the eigensubspace of the lowest N_k eigenfunctions of ${{\mathcal{H}}}_{k}$, as will be demonstrated subsequently. We refer to the “Methods” section for the solution procedure employed to solve the aforementioned variational problem.

Construction of the localized 3-D Tucker tensor basis ${{\mathbb{T}}}^{{\rm{L}}}$

The 1-D localized functions whose span is a close approximation to the subspace spanned by the 1-D eigenfunctions of ${{\mathcal{H}}}_{k}$ are subsequently used to construct the 3-D Tucker tensor basis. Denoting the 1-D localized functions as ${\psi }_{1,{i}_{1}}^{{\rm{L}}}({x}_{1})$, ${\psi }_{2,{i}_{2}}^{{\rm{L}}}({x}_{2})$, ${\psi }_{3,{i}_{3}}^{{\rm{L}}}({x}_{3})$, the 3-D localized tensor-structured basis functions ${T}_{I}^{{\rm{L}}}$ are given by

$${T}_{I}^{{\rm{L}}}({\bf{x}})={\psi }_{1,{i}_{1}}^{{\rm{L}}}({x}_{1}){\psi }_{2,{i}_{2}}^{{\rm{L}}}({x}_{2}){\psi }_{3,{i}_{3}}^{{\rm{L}}}({x}_{3}),$$

(5)

where 1 ≤ i_d ≤ R_d and I is the composite index $I={({i}_{1},{i}_{2},{i}_{3})}_{1\le {i}_{{\mathrm {d}}}\le {R}_{{\mathrm {d}}}}$. The rank of the Tucker tensor basis is given by (R₁, R₂, R₃) which denotes the number of localized 1-D functions in each direction. The space spanned by the 3-D localized tensor-structured basis functions is denoted as ${{\mathbb{T}}}^{{\rm{L}}}$.

Projection of the Kohn–Sham Hamiltonian onto ${{\mathbb{T}}}^{{\rm{L}}}$

The Kohn–Sham Hamiltonian is projected onto ${{\mathbb{T}}}^{{\rm{L}}}$ spanned by the 3-D tensor-structured localized basis functions. We note that the Kohn–Sham effective potential V_eff is a functional of the electron-density ρ, and is comprised of a local-part ${V}_{{\rm{eff}}}^{{\rm{loc}}}$ (local in real-space) and a non-local part ${V}_{{\rm{ext}}}^{{\rm{nl}}}$. ${V}_{{\rm{eff}}}^{{\rm{loc}}}$ includes the Hartree potential (V_H), the exchange-correlation potential and the local-part of the pseudopotential, whereas ${V}_{{\rm{ext}}}^{{\rm{nl}}}$ comprises of the non-local projectors of the pseudopotential (cf. Supplementary Method: Kohn–Sham effective potential computation using tensor-structured techniques). The convolution integral involved in the evaluation of V_H can be efficiently computed using a low-rank Tucker tensor decomposition of the electron-density (R_ρ denoting the rank of the decomposition) and approximating the Coulomb integral by a series of Gaussian functions^14,23 (cf. Supplementary Method: Kohn–Sham effective potential computation using tensor-structured techniques). Subsequently, a low-rank Tucker tensor approximation of ${V}_{{\rm{eff}}}^{{\rm{loc}}}$ and ${V}_{{\rm{ext}}}^{{\rm{nl}}}$ is utilized, with R_V and ${R}_{{\rm{V}}}^{{\rm{nl}}}$ denoting the corresponding ranks, respectively. Denoting the low-rank Tucker approximation of the effective potential V_eff by ${\tilde{V}}_{{\rm{eff}}}$, whose approximation error decays exponentially with the Tucker rank^14,15, the projection of the Kohn–Sham Hamiltonian onto ${{\mathbb{T}}}^{{\rm{L}}}$ is given by

$${\tilde{H}}_{I,J}^{{\rm{L}}}=\left\langle {T}_{I}^{{\rm{L}}}\right|-\frac{1}{2}{\nabla }^{2}+{\tilde{V}}_{{\rm{eff}}}(\rho ;{\bf{R}})\left|{T}_{J}^{{\rm{L}}}\right\rangle \ .$$

(6)

We note that the low-rank representation ${\tilde{V}}_{{\rm{eff}}}$ reduces the integrals involved in Eq. (6) to tensor products of one-dimensional integrals, thereby facilitating the efficient evaluation of Hamiltonian matrix elements (cf. Supplementary Method: Computation of projected Hamiltonian).

The projected Kohn–Sham Hamiltonian matrix elements are computed, and a truncation tolerance is introduced to zero out the Hamiltonian matrix elements below the tolerance. This truncation is performed in every SCF iteration, which improves the sparsity of the Hamiltonian matrix and thereby reducing the memory footprint of the calculation. Furthermore, the sparsity of the Hamiltonian matrix also reduces the computational complexity of the algorithm employed to solve the Kohn–Sham equations, which is discussed subsequently. We note that the error in the ground-state energy, corresponding to the truncation of the Hamiltonian matrix elements, systematically decreases with tighter truncation tolerance. We refer to Supplementary Note 2 (Supplementary Table 2) which provides data to support this observation. Furthermore, we note that a truncation tolerance of 10⁻⁴ Ha provides excellent sparsity in the Hamiltonian, with the error resulting from the truncation being significantly smaller than the basis discretization error and the desired chemical accuracy in ground-state energy (cf. Supplementary Note 2).

Computation of the occupied eigenstates

The discretized Kohn–Sham problem, corresponding to Eq. (1), in the localized orthonormal tensor-structured basis is given by the standard eigenvalue problem

$${{\bf{H}}}^{{\rm{L}}}{{\mathbf{\Psi }}}_{i}={\epsilon }_{i}{{\mathbf{\Psi }}}_{i}\ ,\quad i\in \{1,\ldots ,N\}$$

(7)

where H^L denotes the truncated sparse Kohn–Sham Hamiltonian matrix. We use the Chebyshev filtering-based subspace iteration (ChFSI)²⁴ to efficiently solve the Kohn–Sham equations. The ChFSI method has been demonstrated to be efficient with good parallel scalability for real-space implementations of DFT^25,26,27. In the ChFSI method, in each SCF iteration, a suitably constructed Chebyshev filter using H^L is employed to construct a close approximation to the relevant eigensubspace of the occupied states. The action of the Chebyshev filter on a given subspace can be cast as a recursive iteration involving matrix-vector multiplications between H^L and vectors obtained during the course of recursive iteration. Since H^L is sparse, the computational complexity of the Chebyshev filtering operation scales as ${\mathcal{O}}({R}^{3}N)$, where $R=\max \{{R}_{1},{R}_{2},{R}_{3}\}$. In ChFSI, the Chebyshev filtered vectors are orthogonalized using a Gram–Schmidt orthogonalization procedure, and subsequently the Kohn–Sham eigenstates are computed by projecting H^L onto the Chebyshev-filtered subspace and diagonalizing this projected Hamiltonian. The computational complexity of the orthogonalization procedure and the subspace projection scales as ${\mathcal{O}}({R}^{3}{N}^{2})$ while the diagonalization cost scales as ${\mathcal{O}}({N}^{3})$. As demonstrated in Supplementary Table 3 (cf. Supplementary Note 3), Chebyshev filtering, which scales linearly with N, remains the dominant cost even at 25,000 electrons for the various benchmark examples considered in this work. We note that, at even larger system sizes, other costs that exhibit quadratic-scaling (orthogonalization and subspace projection) and cubic-scaling (diagonalization) with N can start to compete. However, at such a point, explicit diagonalization can be avoided, and already developed ideas¹³ of localizing the Chebyshev-filtered vectors in conjunction with Fermi-operator expansion can be adopted to retain the reduced-order scaling for systems with or without a gap. We refer to the methods section for details on the various numerical parameters employed in conducting the DFT calculations using the SCF iteration approach via the ChFSI technique.

Eigensubspace representability of L ₁ localized 1-D functions

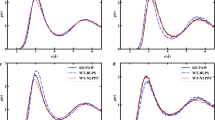
We now demonstrate the ability of the L₁ localized functions to closely approximate the eigensubspace of ${{\mathcal{H}}}_{k}$ using Al₁₄₇ nano-particle with icosahedral symmetry. We compute the additive separable approximation of the Kohn–Sham Hamiltonian for this nano-particle, and, then compute the lowest 70 eigenstates of ${{\mathcal{H}}}_{k}$. We subsequently use the L₁ localization approach to compute the localized functions that are a close approximation to the eigensubspace. Figure 2 shows the lowest five eigenfunctions of ${{\mathcal{H}}}_{1}$ (one of the 1-D separable Hamiltonian) (top) and the corresponding 1-D localized functions (bottom). We refer to Supplementary Note 4 (Supplementary Fig. 1) for an illustration of all 70 eigenstates and the corresponding 1-D localized functions. It is evident that, while the eigenfunctions are global in nature, the functions obtained from the L₁ localization approach are localized in real-space. This locality is key to the sparsity of the Kohn–Sham Hamiltonian matrix in the Tucker tensor basis, and the resulting computational efficiency.

Fig. 2: 1-D functions from separable Hamiltonian.

1-D functions in x₁ direction constructed from the additive separable approximation of the Kohn–Sham Hamiltonian for Al₁₄₇ nano-particle. Top: Lowest five eigenfunctions of ${{\mathcal{H}}}_{1}$. Bottom: The corresponding L₁ localized 1-D functions.

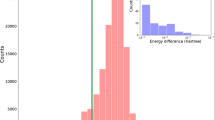
In order to demonstrate the accuracy of the L₁ localization approach in closely approximating the eigensubspace of the separable Hamiltonian, we consider the first 70 eigenstates of ${{\mathcal{H}}}_{1}$ and the eigenvalues of the matrix ${K}_{ij}=\langle {\psi }_{1,i}^{{\rm{L}}}|{{\mathcal{H}}}_{1}|{\psi }_{1,j}^{{\rm{L}}}\rangle$, 1 ≤ i, j, ≤70. Figure 3 shows the eigenvalues of ${{\mathcal{H}}}_{1}$ and the eigenvalues of K_ij. It is interesting to note that the eigenvalues of the first 65 states are almost identical, with only slight deviations for the higher states. This demonstrates that the space spanned by the localization functions obtained using the L₁ localization approach is a close approximation to the eigensubspace of ${{\mathcal{H}}}_{k}$. We also note here that better accuracy can be achieved, when necessary, by simply increasing the size of N_k to be solved for in Eq. (4). In order to assess the accuracy afforded by the localization procedure in the ground-state energy, we computed the ground-state energy of Al₁₄₇ using the 3-D localized basis with rank 70, and compared that with the energy obtained using the eigenbasis of ${{\mathcal{H}}}_{1}+{{\mathcal{H}}}_{2}+{{\mathcal{H}}}_{3}$ (i.e., without localization) of the same rank. The energy obtained without localization is −56.61882 eV per atom in comparison to −56.61893 eV per atom obtained using localization. Thus, the error introduced due to localization is ~0.1 meV per atom, which is substantially smaller than the basis discretization error of ~8.5 meV per atom corresponding to rank 70 (reference energy is −56.6274 eV per atom; cf. Table 1).

Fig. 3: Representability of the 1-D localized functions.

Comparison of the eigenvalues of the 1-D separable Hamiltonian in x₁ direction of Al₁₄₇ nano-particle (marked with blue circle) with the eigenvalues of ${K}_{ij}=\langle {\psi }_{1,i}^{{\rm{L}}}|{{\mathcal{H}}}_{k}|{\psi }_{1,j}^{{\rm{L}}}\rangle$ (marked with red cross and labeld as SOC).

Convergence of the tensor-structured basis

We next investigate the convergence properties of the 3-D Tucker tensor basis constructed from the 1-D localized functions. For the convergence study we consider two benchmark problems: (i) C₆₀ (fullerene) molecule; (ii) tris (bipyridine) ruthenium, a transition metal complex. We note that these systems have no tensor structure symmetry and serve as stringent benchmarks to assess the convergence and accuracy afforded by the proposed Tucker tensor basis. The ground-state energy for these molecules is computed for various Tucker tensor ranks R (R₁ = R₂ = R₃ = R), with the 3-D Tucker tensor basis getting systematically refined with increasing R. In this study, R_ρ, R_V and ${R}_{{\rm{V}}}^{{\rm{nl}}}$ are chosen stringently such that the resulting errors are significantly smaller than the basis discretization errors, and they are held fixed for increasing R. In particular, we used R_ρ = 45, R_V = 65 and ${R}_{{\rm{V}}}^{{\rm{nl}}}=20$ for fullerene, and R_ρ = 80, R_V = 55 and ${R}_{{\rm{V}}}^{{\rm{nl}}}=20$ for tris (bipyridine) ruthenium. The basis discretization error (convergence with respect to R) is measured with respect to a well-converged QE result. The converged QE ground-state energies for fullerene molecule is taken to be −155.1248 eV per atom (E_cut = 60 Ha) and that of tris (bipyridine) ruthenium is taken to be −118.2128 eV per atom (E_cut = 65 Ha).

Figure 4a, b shows the relative error in the ground-state energy for the various ranks of the Tucker tensor basis. It is evident from these results that the Tucker tensor basis constructed using our approach provides an exponential convergence in the ground-state energy with increasing Tucker rank. The convergence study of these molecules suggests that the proposed tensor-structured technique provides systematic convergence with high accuracy and is capable of handling generic materials systems, including those involving transition metals.

Fig. 4: Convergence with respect to the Tucker rank.

a Fullerene and b Tris (bipyridine) ruthenium. The electron-density isocontours are provided in the inset.

Performance and scaling analysis

To study the performance and scaling with system-size of the proposed tensor-structured approach for DFT calculations, we consider two classes of benchmark systems: (i) Aluminum nano-particles of various sizes ranging from 13 atoms to 6525 atoms; (ii) Silicon quantum dots with system-sizes ranging from 26 atoms to 7355 atoms. These benchmark systems constitute materials systems with and without a gap, thus allowing us to assess the system-size scaling for both classes of materials. In order to compare the efficiency of the proposed tensor-structured approach with the widely used plane-wave DFT calculations, we also conducted the DFT calculations using QE wherever possible. For the sake of estimating the computational efficiency, the energy cut-off for QE and the Tucker rank are chosen such that the ground-state energy is converged to within 10 meV per atom measured with respect to a highly converged reference calculation. The reference ground-state energies are obtained from QE (using a high-energy cut-off) for smaller systems and the DFT-FE code²⁶—a massively parallel real-space code for large-scale DFT calculations—for larger system-sizes. The cell size for plane-wave calculations is chosen such that each atom is at least 10 Bohr away from the boundary, which was needed to obtain the desired accuracy.

In these benchmark calculations, the additive separable approximation to the Kohn–Sham Hamiltonian is computed only in the first SCF iteration and the resulting 3-D Tucker basis is held fixed for subsequent SCF iterations. We note that the approximation properties of an adaptive Tucker basis (where the basis is regenerated for every SCF iteration) and the fixed Tucker basis are similar, with the differences in the accuracy being substantially smaller than the basis discretization error for a given Tucker rank. We refer to Supplementary Note 1 (Supplementary Table 1) which provides data supporting this observation. In the tensor-structured calculations reported subsequently, all the numerical parameters—ranks for approximating electron-density and effective Kohn–Sham potential $({R}_{\rho },{R}_{{\rm{V}}},{R}_{{\rm{V}}}^{{\rm{nl}}})$ in ${\tilde{{\bf{H}}}}^{{\rm{L}}}$, and the truncation tolerance adopted in computing H^L—are chosen such that the resulting errors are substantially smaller than the basis discretization error in the ground-state energy associated with the Tucker rank R of the localized 3-D Tucker tensor basis and the desired chemical accuracy. In particular, for the Aluminum nano-particles we used R_ρ = 40, R_V = 50 and ${R}_{{\rm{V}}}^{{\rm{nl}}}=25$. In the case of Silicon quantum dots, we used R_ρ = 55, R_V = 55 and ${R}_{{\rm{V}}}^{{\rm{nl}}}=25$. The truncation tolerance in computing H^L was chosen to be 10⁻⁴ Ha for all the calculations, which provides excellent sparsity for H^L, and, importantly, the sparsity is either steady or improves with increasing system-size (cf. Supplementary Tables 2 and 3). The error in ground-state energy associated with this choice of truncation tolerance is ~1 meV per atom (cf. Supplementary Table 2), as opposed to the targeted accuracy in this study of being within 10 meV per atom of reference energies.

Aluminum nano-particles

The computational efficiency afforded by the proposed tensor-structured approach in comparison to QE for the various aluminum nano-particles with icosahedral symmetry considered in this work is provided in Table 1. We note that the Tucker rank required to achieve the desired accuracy only grows slowly with increasing system-size. Importantly, we note that the number of basis functions needed to achieve the desired accuracy using the localized Tucker basis is smaller than the plane-wave basis. As previously discussed, this is a consequence of the superior approximation properties of the Tucker tensor basis generated as the eigenbasis of an additive separable approximation of the Kohn–Sham Hamiltonian that in addition to the Laplace operator retains some characteristics of the Kohn–Sham potential, as opposed to the plane-wave basis which corresponds to the eigenbasis of the Laplace operator. In terms of the computational time, while QE is more efficient for the smaller system-sizes, the tensor-structured approach starts to substantially outperform for larger system-sizes. Notably, for Al₂₀₅₇, the tensor-structured approach is 8-fold more efficient. Furthermore, using the computational times, the scaling of the proposed tensor-structured approach is estimated to be around ${\mathcal{O}}({N}_{{\rm{e}}}^{1.78})$ with N_e denoting the number of electrons (cf. Fig. 5a). Notably, the scaling with system-size is sub-quadratic for this metallic system over system-sizes spanning many thousands of atoms, as opposed to the cubic-scaling complexity for plane-wave DFT calculations. We note that this is a consequence of the slow growth of the Tucker rank with system-size that results in a sub-linear growth of the total number of basis functions with system-size. The breakdown of the computational costs for the various steps of the calculation is provided in Supplementary Note 3 (cf. Supplementary Table 3).

Fig. 5: Computational complexity of the tensor-structured approach.

a Aluminum nano-particles ${\mathcal{O}}({N}_{{\rm{e}}}^{1.78})$ and b Silicon quantum dots ${\mathcal{O}}({N}_{{\rm{e}}}^{1.8})$.

Silicon quantum dots

Table 2 compares the computational performance of the proposed tensor-structured approach with QE for a wide range of silicon quantum dots passivated with hydrogen. As in the case of aluminum nano-particles, the Tucker tensor basis is more efficient than the plane-wave basis in terms of the number of basis functions to attain the desired accuracy. In terms of computational time, the proposed tensor-structured approach starts competing with QE beyond a few hundred atoms, and significantly outperforms for larger systems. Moreover, the scaling with system-size for the tensor-structured algorithm, for a range of system-sizes with the largest containing 7355 atoms, is estimated to be ${\mathcal{O}}({N}_{{\rm{e}}}^{1.8})$ (cf. Fig. 5b). Notably, this scaling is similar to that obtained for aluminum nano-particles as the algorithm treats systems with and without a gap on a similar footing.

Discussion

We have presented a tensor-structured algorithm, where the Tucker tensor basis is constructed as a tensor product of localized 1-D functions whose span closely approximates the eigensubspace of a suitably constructed additive separable approximation to the Kohn–Sham Hamiltonian. The resulting localized Tucker tensor basis, that is adapted to the Kohn–Sham Hamiltonian, provides a systematically convergent basis as evidenced by the exponential convergence of the ground-state energy with increasing Tucker rank. Our numerical studies on the computational performance suggest that the proposed approach exhibits sub-quadratic scaling (with system-size) over a wide range of system-sizes with the largest involving many thousands of atoms. Importantly, sub-quadratic scaling is realized for both systems with and without a gap, as the algorithm treats both metallic and insulating systems on an equal footing. Further, comparing the computational efficiency of the proposed approach with QE, we observe significant outperformance for system-sizes beyond 5000 electrons.

We note that the sub-quadratic scaling is a consequence of the slow growth of the Tucker rank with system-size, with the resulting number of basis functions growing sub-linearly with system-size even for systems containing many thousands of atoms. By combining the proposed approach with reduced-order scaling techniques that exploit the locality of the wavefunctions in real-space, there is further room to reduce the scaling with system-size and is a useful future direction to pursue. Further, the proposed tensor-structured approach is amenable to GPU acceleration that can further substantially enhance the computational efficiency of the approach, and is currently being pursued. We note that the benchmark systems presented here were restricted to non-periodic calculations as the proposed tensor-structured approach was implemented in a non-periodic setting as a first step of an ongoing effort. However, we remark that the ideas presented here are generic and can be extended to periodic calculations.

Methods

Tucker tensor representation

Tucker tensor representation is a higher-order generalization of principal component analysis for a tensor^28,29,30. An N-way tensor is approximated by a Tucker tensor through Tucker decomposition with a smaller N-way core tensor and N factor matrices whose columns are the rank-1 components from the decomposition^{28,29,30,31,32}. In the scope of this work, the discussion is restricted to three-way tensor. Let $A\in {{\mathbb{R}}}^{{I}_{1}\times {I}_{2}\times {I}_{3}}$ be a real-valued three-way tensor of size I₁ × I₂ × I₃ indexed by a set of integers (i₁, i₂, i₃)

$${A}_{({i}_{1},{i}_{2},{i}_{3})}={a}_{{i}_{1}{i}_{2}{i}_{3}},$$

(8)

where ${i}_{d}\in \{1,2,...,{I}_{d}\},{I}_{d}\in {\mathbb{N}}$ and d ∈ {1, 2, 3} denotes the dimensions. A Tucker tensor representation of the tensor A with decomposition rank R = (R₁, R₂, R₃) for each direction has the form

$$A\approx {A}^{({\bf{R}})}=\mathop{\sum }\limits_{{r}_{1}=1}^{{R}_{1}}\mathop{\sum }\limits_{{r}_{2}=1}^{{R}_{2}}\mathop{\sum }\limits_{{r}_{3}=1}^{{R}_{3}}\sigma {{\bf{u}}}_{1}^{{r}_{1}}\circ {{\bf{u}}}_{2}^{{r}_{2}}\circ {{\bf{u}}}_{3}^{{r}_{3}},$$

(9)

where $\sigma \in {{\mathbb{R}}}^{{R}_{1}\!\times\! {R}_{2}\!\times\! {R}_{3}}$ is the core tensor, ${{\bf{u}}}_{d}^{{r}_{d}}\in {{\mathbb{R}}}^{{I}_{d}}$ forms the factor matrix ${{\bf{U}}}_{d}\in {{\mathbb{R}}}^{{I}_{d}\!\times\! {R}_{d}}$, and "∘" denotes the vector outer product ${({{\bf{u}}}_{1}^{{r}_{1}}\circ {{\bf{u}}}_{2}^{{r}_{2}}\circ {{\bf{u}}}_{3}^{{r}_{3}})}_{{i}_{1},{i}_{2},{i}_{3}}:= {u}_{1,{i}_{1}}^{{r}_{1}}{u}_{2,{i}_{2}}^{{r}_{2}}{u}_{3,{i}_{3}}^{{r}_{3}}$. The core tensor stores the coefficients ${\sigma }_{{r}_{1}{r}_{2}{r}_{3}}$ for each rank-1 tensor ${{\bf{u}}}_{1}^{{r}_{1}}\circ {{\bf{u}}}_{2}^{{r}_{2}}\circ {{\bf{u}}}_{3}^{{r}_{3}}$. The core tensor and the factor matrices can be viewed as the higher-order correspondence of the singular values and unitary matrices. The tensor representation of the Tucker form can be obtained with the higher-order singular value decomposition (HOSVD). The HOSVD flattens the given tensor in three directions and employs singular-value decomposition to obtain the factor matrices. The factor matrices are then used to contract with the given tensor to obtain the core tensor. We refer to³² and³³ for details of HOSVD and further review on tensor decomposition and tensor analysis. In this work, an MPI implementation in C++ for Tucker decomposition is used^34,35.

Computation of L ₁ localized 1-D functions

The variational problem in Eq. (4) is solved by the splitting orthogonality constraint algorithm (SOC). The SOC algorithm introduces two auxiliary variables controlling the orthonormality and the locality constraints and translates the constrained minimization problem into unconstrained problems. The unconstrained problems are then optimized iteratively. The SOC algorithm is capable of providing a set of compressed modes with good locality, yet preserving the orthogonality. We refer to Ozolinš et al.²² and Lai and Osher³⁶ for a detailed discussion, and present the algorithm in the context of this work in the Supplementary Method: SOC Algorithm for the sake of completeness.

Ground-state DFT calculations

All calculations are performed using the norm-conserving Troullier–Martin pseudopotentials in Kleinmann–Bylander form^37,38, and a local density approximation (LDA) for the exchange-correlation functional^39,40,41. In the ChFSI method employed to solve the Kohn–Sham equations, we use a Chebyshev filter constructed using polynomial degree of 10–20 for the various materials systems reported in this study. The n-stage Anderson mixing scheme⁴² is employed in the SCF iteration. We used Fermi–Dirac smearing with T = 500 K for computing the orbital occupancies. The performance benchmarks are obtained on compute nodes comprising of 68-core Intel Xeon Phi Processor 7250 and 96 GB memory per node. All calculations were performed in the good parallel-scaling regime to ensure that the obtained computational times (node-hours) are representative of the computational efficiency of the approach.