Abstract
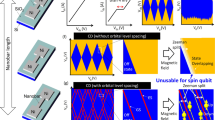
The main characteristics of good qubits are long coherence times in combination with fast operating times. It is well known that carbon-based materials could increase the coherence times of spin qubits, which are among the most developed solid-state qubits. Here, we propose how to form spin qubits in graphene quantum dots. A crucial requirement to achieve this goal is to find quantum-dot states where the usual valley degeneracy in bulk graphene is lifted. We show that this problem can be avoided in quantum dots based on ribbons of graphene with armchair boundaries. The most remarkable new feature of the proposed spin qubits is that, in an array of many qubits, it is possible to couple any two of them via Heisenberg exchange with the others being decoupled by detuning. This unique feature is a direct consequence of the quasi-relativistic spectrum of graphene.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
References
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120–126 (1998).
Elzerman, J. M. et al. Single-shot read-out of an individual electron spin in a quantum dot. Nature 430, 431–435 (2004).
Hanson, R. et al. Single-shot readout of electron spin states in a quantum dot using spin-dependent tunnel rates. Phys. Rev. Lett. 94, 196802 (2005).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Koppens, F. H. L. et al. Driven coherent oscillations of a single electron spin in a quantum dot. Nature 442, 766–771 (2006).
Khaetskii, A. V. & Nazarov, Y. V. Spin relaxation in semiconductor quantum dots. Phys. Rev. B 61, 12639–12642 (2000).
Khaetskii, A. V. & Nazarov, Y. V. Spin-flip transitions between Zeeman sublevels in semiconductor quantum dots. Phys. Rev. B 64, 125316 (2001).
Golovach, V. N., Khaetskii, A. V. & Loss, D. Phonon-induced decay of the electron spin in quantum dots. Phys. Rev. Lett. 93, 016601 (2004).
Burkard, G., Loss, D. & DiVincenzo, D. P. Coupled quantum dots as quantum gates. Phys. Rev. B 59, 2070–2078 (1999).
Erlingsson, S. I., Nazarov, Y. V. & Fal’ko, V. I. Nucleus-mediated spin-flip transitions in GaAs quantum dots. Phys. Rev. B 64, 195306 (2001).
Khaetskii, A. V., Loss, D. & Glazman, L. Electron spin decoherence in quantum dots due to interaction with nuclei. Phys. Rev. Lett. 88, 186802 (2002).
Coish, W. A. & Loss, D. Hyperfine interaction in a quantum dot: Non-Markovian electron spin dynamics. Phys. Rev. B 70, 195340 (2004).
Johnson, A. C. et al. Triplet–singlet spin relaxation via nuclei in a double quantum dot. Nature 435, 925–928 (2005).
Koppens, F. H. L. et al. Control and detection of singlet-triplet mixing in a random nuclear field. Science 309, 1346–1350 (2005).
Min, H. et al. Intrinsic and Rashba spin-orbit interactions in graphene sheets. Phys. Rev. B 74, 165310 (2006).
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005).
Zhang, Y., Tan, Y.-W., Stormer, H. L. & Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 438, 201–204 (2005).
Cheianov, V. V. & Fal’ko, V. I. Selective transmission of Dirac electrons and ballistic magnetoresistance of n–p junctions in graphene. Phys. Rev. B 74, 041403R (2006).
Dombay, N. & Calogeracos, A. Seventy years of the Klein paradox. Phys. Rep. 315, 41–58 (1999).
Katsnelson, M. I., Novoselov, K. S. & Geim, A. K. Klein paradox in graphene. Nature Phys. 2, 620–625 (2006).
McClure, J. W. Diamagnetism of graphite. Phys. Rev. 104, 666–671 (1956).
Semenoff, G. W. Condensed-matter simulation of a three-dimensional anomaly. Phys. Rev. Lett. 53, 2449–2452 (1984).
DiVincenzo, D. P. & Mele, E. J. Self-consistent effective-mass theory for intralayer screening in graphite intercalation compounds. Phys. Rev. B 29, 1685–1694 (1984).
Silvestrov, P. G. & Efetov, K. B. Quantum dots in graphene. Phys. Rev. Lett. 98, 016802 (2007).
Nilsson, J., Castro Neto, A. H., Guinea, F. & Peres, N. M. R. Transmission through a biased graphene bilayer barrier. Preprint at <http://www.arxiv.org/cond-mat/0607343> (2006).
De Martino, A., Dell’Anna, L. & Egger, R. Magnetic confinement of massless Dirac fermions in graphene. Preprint at <http://www.arxiv.org/cond-mat/0610290> (2006).
Brey, L. & Fertig, H. A. Electronic states of graphene nanoribbons studied with the Dirac equation. Phys. Rev. B 73, 235411 (2006).
Tworzydło, J., Trauzettel, B., Titov, M., Rycerz, A. & Beenakker, C. W. J. Quantum-limited shot noise in graphene. Phys. Rev. Lett. 96, 246802 (2006).
Grabert, H. & Devoret, M. H. (eds) Single Charge Tunnelling (Plenum, New York, 1991).
Svore, K. M., Terhal, B. M. & DiVincenzo, D. P. Local fault-tolerant quantum computation. Phys. Rev. A 72, 022317 (2005).
Acknowledgements
We thank H. A. Fertig and L. M. K. Vandersypen for discussions and acknowledge support from the Swiss NSF, NCCR Nanoscience, DARPA, ONR and JST ICORP.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
About this article
Cite this article
Trauzettel, B., Bulaev, D., Loss, D. et al. Spin qubits in graphene quantum dots. Nature Phys 3, 192–196 (2007). https://doi.org/10.1038/nphys544
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys544