Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Multicomponent fractional quantum Hall effect in graphene

Nature Physics volume 7, pages 693–696 (2011)Cite this article

Abstract

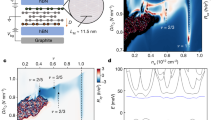
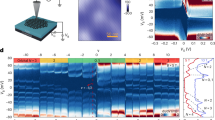
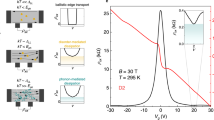
The fractional quantum Hall effect1,2,3,4 (FQHE) in an electron gas with multiple internal degrees of freedom provides a model system to study the interplay between symmetry breaking and emergent topological order5. In graphene, the structure of the honeycomb lattice endows the electron wavefunctions with an additional quantum number, termed valley isospin, which, combined with the usual electron spin, yields four-fold degenerate Landau levels (LLs; refs 6, 7). This additional symmetry modifies the FQHE and is conjectured to produce new incompressible ground states in graphene8,9,10,11,12,13,14,15,16,17. Here we report multiterminal measurements of the FQHE in high-mobility graphene devices fabricated on hexagonal boron nitride substrates18. The measured energy gaps are large, particularly in the second Landau level, where they are up to 10 times larger than those reported in the cleanest conventional systems. In the lowest Landau level the hierarchy of FQH states reflects the additional valley degeneracy.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Magnetotransport.
Figure 2: Fractional quantum Hall effect.
Figure 3: Energy gaps.

Similar content being viewed by others

References

  1. Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982).

    Article  ADS  Google Scholar 

  2. Laughlin, R. B. Anomalous quantum Hall effect: An incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 50, 1395–1398 (1983).

    Article  ADS  Google Scholar 

  3. Halperin, B. Theory of the quantized Hall conductance. Helv. Phys. Acta 56, 75–102 (1983).

    Google Scholar 

  4. Jain, J. K. Composite-fermion approach for the fractional quantum Hall effect. Phys. Rev. Lett. 63, 199–202 (1989).

    Article  ADS  Google Scholar 

  5. Das Sarma, S. & Pinczuk, A. Perspectives in Quantum Hall Effects (Wiley, 1997).

    Google Scholar 

  6. Novoselov, K. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005).

    Article  ADS  Google Scholar 

  7. Zhang, Y., Tan, Y., Stormer, H. & Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 438, 201–204 (2005).

    Article  ADS  Google Scholar 

  8. Toke, C., Lammert, P. E., Crespi, V. H. & Jain, J. K. Fractional quantum Hall effect in graphene. Phys. Rev. B 74, 235417 (2006).

    Article  ADS  Google Scholar 

  9. Yang, K., Das Sarma, S. & MacDonald, A. H. Collective modes and skyrmion excitations in graphene SU(4) quantum Hall ferromagnets. Phys. Rev. B 74, 075423 (2006).

    Article  ADS  Google Scholar 

  10. Nomura, K. & MacDonald, A. H. Quantum Hall ferromagnetism in graphene. Phys. Rev. Lett. 96, 256602 (2006).

    Article  ADS  Google Scholar 

  11. Apalkov, V. M. & Chakraborty, T. Fractional quantum Hall states of Dirac electrons in graphene. Phys. Rev. Lett. 97, 126801 (2006).

    Article  ADS  Google Scholar 

  12. Goerbig, M. O. & Regnault, N. Analysis of a SU(4) generalization of Halperin’s wave function as an approach towards a SU(4) fractional quantum Hall effect in graphene sheets. Phys. Rev. B 75, 241405 (2007).

    Article  ADS  Google Scholar 

  13. Khveshchenko, D. V. Composite Dirac fermions in graphene. Phys. Rev. B 75, 153405 (2007).

    Article  ADS  Google Scholar 

  14. Toke, C. & Jain, J. K. SU(4) composite fermions in graphene: Fractional quantum Hall states without analog in GaAs. Phys. Rev. B 75, 245440 (2007).

    Article  ADS  Google Scholar 

  15. Shibata, N. & Nomura, K. Coupled charge and valley excitations in graphene quantum Hall ferromagnets. Phys. Rev. B 77, 235426 (2008).

    Article  ADS  Google Scholar 

  16. Shibata, N. & Nomura, K. Fractional quantum Hall effects in graphene and its bilayer. J. Phys. Soc. Jpn 78, 104708 (2009).

    Article  ADS  Google Scholar 

  17. Papić, Z., Goerbig, M. O. & Regnault, N. Atypical fractional quantum Hall effect in graphene at filling factor 1/3. Phys. Rev. Lett. 105, 176802 (2010).

    Article  ADS  Google Scholar 

  18. Dean, C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nature Nanotech. 5, 722–726 (2010).

    Article  ADS  Google Scholar 

  19. Zhang, Y. et al. Landau-level splitting in graphene in high magnetic fields. Phys. Rev. Lett. 96, 136806 (2006).

    Article  ADS  Google Scholar 

  20. Du, X., Skachko, I., Duerr, F., Luican, A. & Andrei, E. Y. Fractional quantum Hall effect and insulating phase of Dirac electrons in graphene. Nature 462, 192–195 (2009).

    Article  ADS  Google Scholar 

  21. Bolotin, K. I., Ghahari, F., Shulman, M. D., Stormer, H. L. & Kim, P. Observation of the fractional quantum Hall effect in graphene. Nature 462, 196–199 (2009).

    Article  ADS  Google Scholar 

  22. Checkelsky, J. G., Li, L. & Ong, N. P. Zero-energy state in graphene in a high magnetic field. Phys. Rev. Lett. 100, 206801 (2008).

    Article  ADS  Google Scholar 

  23. Ghahari, F., Zhao, Y., Cadden-Zimansky, P., Bolotin, K. & Kim, P. Measurement of the ν=1/3 fractional quantum Hall energy gap in suspended graphene. Phys. Rev. Lett. 106, 046801 (2011).

    Article  ADS  Google Scholar 

  24. Goerbig, M. O., Moessner, R. & Douçot, B. Electron interactions in graphene in a strong magnetic field. Phys. Rev. B 74, 161407 (2006).

    Article  ADS  Google Scholar 

  25. Dethlefsen, A. F., Mariani, E., Tranitz, H-P., Wegscheider, W. & Haug, R. J. Signatures of spin in the ν=1/3 fractional quantum Hall effect. Phys. Rev. B 74, 165325 (2006).

    Article  ADS  Google Scholar 

  26. Ando, T. Screening effect and impurity scattering in monolayer graphene. J. Phys. Soc. Jpn 75, 074716 (2006).

    Article  ADS  Google Scholar 

  27. Kumar, A., Manfra, M. J., Csáthy, G. A., Pfeiffer, L. N. & West, K. W. Nonconventional odd denominator fractional quantum Hall states in the second Landau level. Phys. Rev. Lett. 105, 246808 (2010).

    Article  ADS  Google Scholar 

  28. Padmanabhan, M., Gokmen, T. & Shayegan, M. Composite fermion valley polarization energies: Evidence for particle–hole asymmetry. Phys. Rev. B 81, 113301 (2010).

    Article  ADS  Google Scholar 

  29. Lai, K., Pan, W., Tsui, D. C. & Xie, Y-H. Fractional quantum Hall effect at ν=2/3 and 4/3 in strained Si quantum wells. Phys. Rev. B 69, 125337 (2004).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank J. K. Jain, C. Toke, N. Shibata, M. O. Goerbig and M. Foster for discussions, J. Sanchez-Yamagishi and P. Jarillo-Herrero for fabrication advice regarding the PVA, and I. Meric, Z. Kagan, A. Tsoi, N. Baklitskaya and I. Mendonca for help with the device preparation. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation Cooperative Agreement No. DMR-0654118, the State of Florida and the US Department of Energy. This work is supported by DARPA CERA, AFOSR MURI, FCRP through C2S2 and FENA, NSEC (No. CHE-0117752) and NYSTAR. P.K. and A.F.Y. acknowledge support from DOE (DE-FG02-05ER46215).

Author information

Author notes

  1. C. R. Dean and A. F. Young: These authors contributed equally to this work

Authors and Affiliations

  1. Department of Electrical Engineering, Columbia University, New York, New York 10027, USA

    C. R. Dean & K. L. Shepard

  2. Department of Mechanical Engineering, Columbia University, New York, New York 10027, USA

    C. R. Dean, L. Wang & J. Hone

  3. Department of Physics, Columbia University, New York, New York 10027, USA

    A. F. Young, P. Cadden-Zimansky, H. Ren & P. Kim

  4. National High Magnetic Field Laboratory, Tallahassee, Florida 32310, USA

    P. Cadden-Zimansky

  5. Advanced Materials Laboratory, National Institute for Materials Science, 1-1 Namiki, Tsukuba 305-0044, Japan

    K. Watanabe & T. Taniguchi

Authors
  1. C. R. Dean
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. A. F. Young
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. P. Cadden-Zimansky
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. L. Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. H. Ren
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. K. Watanabe
    View author publications

    You can also search for this author inPubMed Google Scholar

  7. T. Taniguchi
    View author publications

    You can also search for this author inPubMed Google Scholar

  8. P. Kim
    View author publications

    You can also search for this author inPubMed Google Scholar

  9. J. Hone
    View author publications

    You can also search for this author inPubMed Google Scholar

  10. K. L. Shepard
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

C.R.D. and A.F.Y. performed all experiments including sample fabrication and measurement, and wrote the paper. P.C-Z. contributed to sample measurement. L.W. and H.R. contributed to sample fabrication. K.W. and T.T. synthesized the h-BN samples. J.H., P.K. and K.L.S. advised on experiments.

Corresponding author

Correspondence to P. Kim.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 199 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dean, C., Young, A., Cadden-Zimansky, P. et al. Multicomponent fractional quantum Hall effect in graphene. Nature Phys 7, 693–696 (2011). https://doi.org/10.1038/nphys2007

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphys2007

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing