Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Multiple-length-scale elastic instability mimics parametric resonance of nonlinear oscillators

Nature Physics volume 7, pages 56–60 (2011)Cite this article

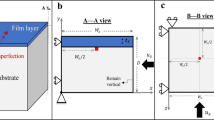
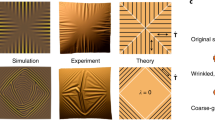
Abstract

Spatially confined rigid membranes reorganize their morphology in response to the imposed constraints. A crumpled elastic sheet presents a complex pattern of random folds focusing the deformation energy1, whereas compressing a membrane resting on a soft foundation creates a regular pattern of sinusoidal wrinkles with a broad distribution of energy2,3,4,5,6,7,8. Here, we study the energy distribution for highly confined membranes and show the emergence of a new morphological instability triggered by a period-doubling bifurcation. A periodic self-organized focalization of the deformation energy is observed provided that an up–down symmetry breaking, induced by the intrinsic nonlinearity of the elasticity equations, occurs. The physical model, exhibiting an analogy with parametric resonance in a nonlinear oscillator, is a new theoretical toolkit to understand the morphology of various confined systems, such as coated materials or living tissues, for example wrinkled skin3, internal structure of lungs9, internal elastica of an artery10, brain convolutions11,12 or formation of fingerprints13. Moreover, it opens the way to a new kind of microfabrication design of multiperiodic or chaotic (aperiodic) surface topographythrough self-organization.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Evolution of morphologies, wavelengths and amplitudes with compression.
Figure 2: Predictions of the model and comparison with experimental profiles.
Figure 3: Additional consequences of the up–down symmetry breaking for wrinkled patterns.

Similar content being viewed by others

References

  1. Witten, T. A. Stress focusing in elastic sheets. Rev. Mod. Phys. 79, 643–675 (2007).

    Article  ADS  MathSciNet  Google Scholar 

  2. Bowden, N., Brittain, S., Evans, A. G., Hutchinson, J. W. & Whitesides, G. M. Spontaneous formation of ordered structures in thin films of metals supported on an elastomeric polymer. Nature 393, 146–149 (1998).

    Article  ADS  Google Scholar 

  3. Cerda, E. & Mahadevan, L. Geometry and physics of wrinkling. Phys. Rev. Lett. 90, 074302 (2003).

    Article  ADS  Google Scholar 

  4. Vandeparre, H. et al. Slippery or sticky boundary conditions: Control of wrinkling in metal-capped thin polymer films by selective adhesion to substrates. Phys. Rev. Lett. 99, 188302 (2007).

    Article  ADS  Google Scholar 

  5. Vandeparre, H. & Damman, P. Wrinkling of stimuloresponsive surfaces: Mechanical instability coupled to diffusion. Phys. Rev. Lett. 101, 124301 (2008).

    Article  ADS  Google Scholar 

  6. Huang, J. et al. Capillary wrinkling of floating thin polymer films. Science 317, 650–653 (2007).

    Article  ADS  Google Scholar 

  7. Jiang, H. et al. Finite deformation mechanics in buckled thin films on compliant supports. Proc. Natl Acad. Sci. 104, 15607–15612 (2007).

    Article  ADS  Google Scholar 

  8. Pocivavsek, L. et al. Stress and fold localization in thin elastic membranes. Science 320, 912–916 (2008).

    Article  ADS  Google Scholar 

  9. Diamant, H., Witten, T. A., Ege, C., Gopal, A. & Lee, K. Y. C. Topography and instability of monolayers near domain boundaries. Phys. Rev. E 63, 061602 (2001).

    Article  ADS  Google Scholar 

  10. Strupler, M. et al. Second harmonic microscopy to quantify renal interstitial brosis and arterial remodeling. J. Biomed. Opt. 13, 054041 (2008).

    Article  ADS  Google Scholar 

  11. Richman, D. P., Stewart, R. M., Hutchinson, J. W. & Caviness, V. S. Jr Mechanical model of brain convolutional development. Science 189, 18–21 (1975).

    Article  ADS  Google Scholar 

  12. Toro, R. & Burnod, Y. A morphogenetic model for the development of cortical convolutions. Cereb. Cortex 15, 1900–1913 (2005).

    Article  Google Scholar 

  13. Kücken, M. & Newell, A. C. A model for fingerprint formation. Europhys. Lett. 68, 141–146 (2004).

    Article  ADS  Google Scholar 

  14. Efimenko, K. et al. Nested self-similar wrinkling patterns in skins. Nature Mater. 4, 293–297 (2005).

    Article  ADS  Google Scholar 

  15. Feigenbaum, M. J. Quantitative universality for a class of nonlinear transformations. J. Stat. Phys. 19, 25–52 (1978).

    Article  ADS  MathSciNet  Google Scholar 

  16. Feigenbaum, M. J. The universal metric properties of nonlinear transformations. J. Stat. Phys. 21, 669–706 (1979).

    Article  ADS  MathSciNet  Google Scholar 

  17. Libchaber, A., Laroche, C. & Fauve, S. Period doubling cascade in mercury, a quantitative measurement. J. Physique 43, L211–L216 (1982).

    Google Scholar 

  18. Guevara, M. R., Glass, L. & Shrier, A. Phase locking, period-doubling bifurcations, and irregular dynamics in periodically stimulated cardiac cells. Science 214, 1350–1353 (1981).

    Article  ADS  Google Scholar 

  19. Fox, J. J., Bodenschatz, E. & Gilmour, R. F. Period-doubling instability and memory in cardiac tissue. Phys. Rev. Lett. 89, 138101 (2002).

    Article  ADS  Google Scholar 

  20. Berger, C. M. et al. Period-doubling bifurcation to alternans in paced-cardiac tissue: Crossover from smooth to border-collision characteristics. Phys. Rev. Lett. 99, 058101 (2007).

    Article  ADS  Google Scholar 

  21. Melo, F., Umbanhowar, P. B. & Swinney, H. L. Hexagons, kinks, and disorder in oscillated granular layers. Phys. Rev. Lett. 75, 3838–3841 (1995).

    Article  ADS  Google Scholar 

  22. Venkataramani, S. C. & Ott, E. Spatiotemporal bifurcation phenomena with temporal period doubling: Patterns in vibrated sand. Phys. Rev. Lett. 80, 3495–3498 (1998).

    Article  ADS  Google Scholar 

  23. Gilet, T. & Bush, J. Chaotic bouncing of a droplet on a soap film. Phys. Rev. Lett. 102, 014501 (2009).

    Article  ADS  Google Scholar 

  24. Losert, W., Shi, B. Q. & Cummins, H. Z. Spatial period-doubling instability of dendritic arrays in directional solidification. Phys. Rev. Lett. 77, 889–891 (1996).

    Article  ADS  Google Scholar 

  25. Hutchinson, J. W. & Koiter, W. T. Postbuckling theory. Appl. Mech. Rev. 23, 1353–1366 (1970).

    Google Scholar 

  26. Groenewold, J. Wrinkling of plates coupled with soft elastic media. Physica A 298, 32–45 (2001).

    Article  ADS  MathSciNet  Google Scholar 

  27. McLachlan, N. W. Theory and Application of Mathieu Functions (Dover, 1962).

    Google Scholar 

  28. Blanch, G. Chapter 20: Mathieu Functions. in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (ed. Abramowitz, M.) (Dover, 1972).

    Google Scholar 

  29. Sanmartín, J. R. O Botafumeiro: Parametric pumping in the middle ages. Am. J. Phys. 52, 937–945 (1984).

    Article  ADS  Google Scholar 

  30. Van den Broeck, C. & Bena, I. in Stochastic Processes in Physics, Chemistry, and Biology 557 (eds Freund, J. A. & Pöschel, T.) 257–267 (Lect. Notes Phys., 2000).

    Book  Google Scholar 

Download references

Acknowledgements

The authors thank T. Witten, B. Davidovitch, H. Diamant, S. Desprez, C. Troetsler, S. Gabriele and G. Carbone for discussions. This work was supported by the Belgian National Funds for Scientific Research (Mandat Impulsion Scientifique), the Government of the Region of Wallonia (CORRONET and REMANOS Research Programmes) and the European Science Foundation (Eurocores FANAS programme, EBIOADI collaborative research project). F.B. acknowledges financial support from a return grant delivered by the Federal Scientific Politics.

Author information

Authors and Affiliations

  1. Laboratoire Interfaces & Fluides Complexes, CIRMAP, Université de Mons — UMONS, 20 Place du Parc, B-7000 Mons, Belgium

    Fabian Brau, Hugues Vandeparre, Abbas Sabbah, Christophe Poulard & Pascal Damman

  2. Laboratoire de Physique Statistique, Ecole Normale Supérieure, UPMC Paris 06, Université Paris Diderot, CNRS, 24 rue Lhomond, 75005 Paris, France

    Arezki Boudaoud

Authors
  1. Fabian Brau
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hugues Vandeparre
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Abbas Sabbah
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Christophe Poulard
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Arezki Boudaoud
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Pascal Damman
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

F.B. and P.D. designed the experiments; F.B., H.V., A.S. and C.P. carried out the experiments; F.B., A.B. and P.D. developed the theoretical model; F.B. and P.D. wrote the manuscript.

Corresponding author

Correspondence to Pascal Damman.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 508 kb)

Supplementary Information

Supplementary Movie 1 (MOV 552 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Brau, F., Vandeparre, H., Sabbah, A. et al. Multiple-length-scale elastic instability mimics parametric resonance of nonlinear oscillators. Nature Phys 7, 56–60 (2011). https://doi.org/10.1038/nphys1806

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphys1806

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing