Statistical inference for noisy nonlinear ecological dynamic systems

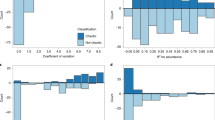
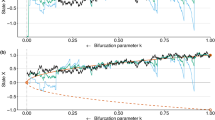
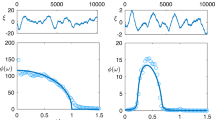
Abstract

Chaotic ecological dynamic systems defy conventional statistical analysis. Systems with near-chaotic dynamics are little better. Such systems are almost invariably driven by endogenous dynamic processes plus demographic and environmental process noise, and are only observable with error. Their sensitivity to history means that minute changes in the driving noise realization, or the system parameters, will cause drastic changes in the system trajectory¹. This sensitivity is inherited and amplified by the joint probability density of the observable data and the process noise, rendering it useless as the basis for obtaining measures of statistical fit. Because the joint density is the basis for the fit measures used by all conventional statistical methods², this is a major theoretical shortcoming. The inability to make well-founded statistical inferences about biological dynamic models in the chaotic and near-chaotic regimes, other than on an ad hoc basis, leaves dynamic theory without the methods of quantitative validation that are essential tools in the rest of biological science. Here I show that this impasse can be resolved in a simple and general manner, using a method that requires only the ability to simulate the observed data on a system from the dynamic model about which inferences are required. The raw data series are reduced to phase-insensitive summary statistics, quantifying local dynamic structure and the distribution of observations. Simulation is used to obtain the mean and the covariance matrix of the statistics, given model parameters, allowing the construction of a ‘synthetic likelihood’ that assesses model fit. This likelihood can be explored using a straightforward Markov chain Monte Carlo sampler, but one further post-processing step returns pure likelihood-based inference. I apply the method to establish the dynamic nature of the fluctuations in Nicholson’s classic blowfly experiments^3,4,5.