Main

The features of superconductivity are mostly governed by the superconducting (SC) gap Δ, or equivalently, by the SC wavefunction, which takes complex values with amplitude and phase degrees of freedom. Nematic superconductivity is characterized by spontaneous rotational-symmetry breaking (RSB) in the amplitude of the SC gap8 (Fig. 1a). Thus, once a nematic superconductor is cooled below its SC transition temperature Tc, RSB in various bulk properties is expected to emerge, while the RSB is absent in the normal (N) state9. We emphasize that nematic superconductors are distinct from known ‘unconventional’ superconductors such as p-wave or d-wave superconductors2, in which spontaneous RSB occurs only in the phase factor of Δ, and thus phase-sensitive junction techniques are required to detect it10. Nematic superconductivity is also different from nematicity originating from the properties of normal-state conduction electrons recently found in various systems3,4,5,6. Materials realization of nematic superconductivity has never been reported (see Supplementary Note 12 for details).

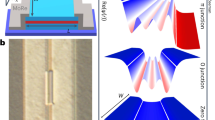
Figure 1: Candidate material for nematic superconductivity: CuxBi2Se3.
figure 1

a, Comparison of nematic and ordinary superconductivity in a hexagonal crystal system, with a nematic liquid-crystal phase and an ordinary liquid phase. The thickness of the blue region in the top panels illustrates the superconducting gap amplitude in the reciprocal space. The grey ovals in the bottom panels represent molecules in a liquid-crystal system. b, Crystal structure of CuxBi2Se3 with x ∼ 0.3. The structure of the quintuple layer (QL) is shown in the right bottom figure. c, Definitions of the axes and field angles with respect to the crystal structure. The purple spheres represent Bi atoms. d, Schematic description of SC gap structures Δ1, Δ2, Δ3, Δ4x and Δ4y proposed for CuxBi2Se3 in refs 7,13. The ovals are Fermi surfaces, whose surface colour represents the gap magnitude, with black indicating Δk = 0.

Full size image

Among known superconductors, the copper-doped topological insulator CuxBi2Se3 (ref. 11), consisting of triangular-lattice layers of Bi and Se with intercalated Cu between layers (Fig. 1b, c), is rather unique. In addition to the ordinary s-wave SC state Δ1, possible unconventional odd-parity SC states, labelled Δ2, Δ3, Δ4x, and Δ4y, originating from strong spin–orbit interactions and its multi-orbital nature have been proposed (Fig. 1d)7,12,13. These odd-parity states can be also categorized as topological SC states, which are accompanied by stable surface states originating from the non-trivial topology of the SC wavefunction. Among these states, the Δ4x and Δ4y states are predicted to be nematic SC states with a non-zero nematic order parameter8. Experimentally, the zero-bias conductance peak observed in the point-contact spectroscopy, indicating the existence of unusual surface states, evidences topological superconductivity14. On the other hand, a scanning tunnelling microscopy (STM) experiment on the ab-plane revealed s-wave-like tunnelling spectra15, which was later actually found to be inconsistent with the s-wave (Δ1) scenario16. Rather, it was proposed that the STM spectra may be explained within the topological superconductivity scenario by taking into account the possible quasi-two-dimensional (Q2D) nature of the Fermi surface12,17. More recently, by means of the nuclear-magnetic resonance (NMR), spin-rotational symmetry was revealed to be broken in the SC state18, suggesting realization of the Δ4x or Δ4y states.

In this Letter, based on the high-resolution specific-heat C measurements of single-crystalline CuxBi2Se3 (Tc ≈ 3.2 K) under accurate two-axis field-directional control using a vector magnet with a rotating stage19, we report thermodynamic evidence for spontaneous RSB in the SC gap amplitude for the first time among any known superconductors. We further obtained evidence for the Δ4y state, with gap minima (or nodes) along one of the Bi–Bi bonding directions. Our results unambiguously show that CuxBi2Se3 belongs to a new class of materials with odd-parity nematicity and topological superconductivity. We emphasize that the conclusion holds irrespectively of the dimensionality of the actual normal-state electronic structure (see Supplementary Note 9).

In Fig. 2a, we compare the dependence of C/T on the in-plane field angle φ for Sample #1 in the SC and N states. Here, as shown in Fig. 1c, we define the x-axis as one of the six equivalent Bi–Bi bond directions within the ab-plane, the y-axis as the direction perpendicular to x within the plane, and φ as the azimuthal angle of the field with respect to x. In addition, the z-axis is parallel to the c-axis and the angle θ is the polar angle with respect to z. Although C/T is independent of φ in the N state, C(φ)/T in the SC state unexpectedly exhibits clear two-fold oscillation. For the rhombohedral crystal symmetry of CuxBi2Se3, C(φ)/T should exhibit six-fold oscillation. Thus, the observed two-fold oscillation in C(φ)/T clearly breaks the rotational symmetry of the underlying lattice. The RSB is more easily recognized in the polar plot of C(φ)/T in Fig. 2b. A possible extrinsic origin for such RSB is field misalignment with respect to the ab-plane. To examine this possibility, we measured the dependence of C on the polar angle θ for various φ, presented as a surface colour plot in Fig. 2c (also see Supplementary Fig. 3). Evidently, C(θ)/T exhibits minima at θ = 90° for any φ, excluding the possibility of field misalignment. In addition, the two-fold oscillation has been reproduced in several samples (Supplementary Fig. 7). Furthermore, one sample (#3) exhibits shifted and smaller oscillations, indicating the existence of multiple ‘nematic domains’, which manifest the spontaneous nature of the RSB (see Supplementary Note 7). Therefore, the rotational symmetry of the lattice is intrinsically and spontaneously broken in the SC state, evidencing nematic superconductivity in CuxBi2Se3.

Figure 2: Evidence for nematic superconductivity in CuxBi2Se3.
figure 2

a, Oscillation of the specific heat at 0.6 K versus in-plane magnetic field angle in the SC state (0.3 T, blue points) compared to the data in the N state (3.5 T, grey points). Here, ΔC(φ) /T is defined as C(φ) /T − C(H ∥ x) /T and the data at 3.5 T are vertically shifted by 0.1 mJ K−2 mol−1. The broken curve is the fitting result with ΔC(φ)/T = A0 + A2 cos(2φ). The data are obtained by averaging the specific-heat signal for typically 30–60 s, and the error bars indicate the standard deviation of the acquired raw data. b, Polar plot of ΔC(φ)/T at 0.6 K and 0.3 T (H ∥ ab), together with the fitting result. The polar angle of a data point in this 2D plot corresponds to the azimuthal field angle φ, and the distance from the origin indicates the magnitude of ΔC/T. c, Colour map of ΔC(θ, φ)/T on a sphere in the Hx–Hy–Hz space, based on the θ-sweep data at 0.6 K and 0.3 T (see also Supplementary Fig. 3a). d, In-plane anisotropy of Hc2 at 0.6 K. The definition of the error bars is explained in Supplementary Fig. 10. The broken curve presents the result of fitting with Hc2(φ) = H0 + H2 cos(2φ) + H6 cos(6φ). e, In-plane magnetic-field dependence of the specific heat for various φ. The arrows mark Hc2. The inset presents data in the whole field range.

Full size image

Next, we discuss the in-plane anisotropy of Hc2 presented in Fig. 2d. In Fig. 2e, we present the field-strength dependence of C/T at 0.6 K for various in-plane field directions. Clearly, C(H)/T curves again do not obey the expected six-fold rotational symmetry: the curves are substantially different between φ = 0° and 60°. We here define Hc2 as the onset of deviation from the linear field dependence in the N state (see Supplementary Note 10). The obtained Hc2(φ) (Fig. 2d) is clearly dominated by two-fold oscillation. Indeed, by fitting Hc2(φ) with H0 + H2 cos(2φ) + H6 cos(6φ), we obtain μ0H0 = 2.37 ± 0.03 T, μ0H2 = 0.37 ± 0.04 T, and μ0H6 = −0.05 ± 0.04 T. Interestingly, H2 is as large as 16% of H0. This striking in-plane Hc2 anisotropy not only supports the nematic SC state of CuxBi2Se3, but also indicates the existence of a single nematic domain in this sample (see Supplementary Note 7).

As one can clearly see in Fig. 2, the observed in-plane field-angle dependences of C and Hc2 are both dominated by the two-fold components. The large two-fold behaviour is probably due to the dominance of the two-fold component originating from the nematic SC order parameter over the ordinary component, such as the one originating from Fermi-surface anisotropy, as discussed in Supplementary Note 13.

Among the proposed SC states for CuxBi2Se3, only the Δ4x and Δ4y states spontaneously break the in-plane rotational symmetry8,9. Thus, the observed bulk nematicity provides strong evidence for the two possible nematic states, the nodal Δ4x state (with nodes along the ky-direction, protected by the mirror symmetry8) and the fully gapped Δ4y state (with gap minima along the kx-direction; also see Supplementary Note 9) can be distinguished by the position of the gap minima or nodes. With this aim in mind, we investigate C(φ)/T of Sample #1, with a single nematic domain, in more detail. When the SC gap has minima (including nodes), C/T exhibits oscillatory behaviour as a function of field angle, because of the field-angle-dependent quasiparticle excitations originating from the gap anisotropy20,21. At low-temperature and low-field conditions, C/T exhibits minima when the field is parallel to the Fermi velocity at a gap minimum vFmin, as shown in Fig. 3d. Furthermore, it has been predicted and observed that, in addition to the C/T oscillation originating from Hc2 anisotropy, the C/T oscillations exhibit sign changes depending on the temperature and field conditions: for example, at intermediate temperatures, C/T exhibits maxima for H ∥ vFmin (refs 22,23). Thus, detailed experiments as well as comparison with theoretical calculations are required to conclude the gap structure.

Figure 3: Superconducting gap structure of CuxBi2Se3.
figure 3

a–c, Experimental ΔC(φ) /T data compared to fitting results with A0 + A2 cos (2φ) (broken curves). Each curve is shifted vertically by 0.4 mJ K−2 mol−1. Notice that the sample is entirely in the N state at 3.0 T but is in the SC state near φ = 0° at 2.5 T due to the Hc2 anisotropy (see Fig. 2e). The vertical arrows indicate minimum positions in ΔC(φ)/T. For the definition of the error bars, see the caption of Fig. 2a. d, Schematics of the field-angle-dependent quasiparticle excitation (red dots) in the low-temperature and low-field limit. e, Colour map of A2 within the SC phase. In the blue and red regions, ΔC(φ)/T exhibits minima at φ = 0° and 90°, respectively. The circles and squares indicate Hc2 along x and y. The definition of the error bars in Hc2 is explained in Supplementary Fig. 9. f,g, Calculated ΔCcal(φ)/T ≡ Ccal(φ)/T − Ccal(φmin)/T with offsets. Here, Ccal is the calculated specific heat and φmin is the field direction where H ∥ vFmin. The solid and broken curves are for point minima (Δmin/Δmax = 0.1) and for point nodes, respectively. h, Colour map of for point-node gap. In the blue and red regions, ΔCcal(φ)/T exhibits a minimum and maximum at φ = φmin, respectively.

Full size image

Figure 3a–c represents the observed C(φ)/T curves in various conditions. Two-fold oscillation with a minimum at φ = 0° (H ∥ x) is observed at 0.6 K in the SC state. However, at higher temperatures, the oscillation inverts sign above ∼1.5–2.0 T at 1.0 K and ∼1.0 T at 1.5 K, exhibiting a maximum at φ = 0°. The temperature and field dependence of the oscillation prefactor A2 is summarized in Fig. 3e as a colour plot. A boundary between positive and negative A2 exists within the SC phase. These observations are compared with theoretical calculations based on the Kramer–Pesch approximation in Fig. 3f, g. Here, we assume a gap structure with gap minima or point nodes along an in-plane direction φ = φmin on a spherical Fermi surface. The calculated C(φ)/T curves for both cases of gap minima and nodes resemble the observed ones fairly well: they exhibit two-fold oscillation with a minimum for φ = φmin at low temperatures and low fields, and reversed oscillation with a maximum for φ = φmin at elevated temperatures. This oscillation inversion is due to contributions from the density of states at finite energies, as well as of quasiparticle scattering by vortices22. As shown in Fig. 3h, the phase-inversion line passes T/Tc ∼ 0.35 near H/Hc2 = 0 and T/Tc ∼ 0.15 near H/Hc2 = 0.25, again qualitatively similar to the observation (Fig. 3e).

From these agreements between experiment and theory, we conclude that the SC gap of CuxBi2Se3 is Δ4y, possessing gap minima or nodes lying along the kx-direction. Although it is not straightforward to distinguish gap minima or nodes from our data alone, it is more natural to expect that the Δ4y state is fully gapped to have gap minima, due to symmetry and energetic reasons8 (see Supplementary Note 9).

The odd-parity nematic SC state in CuxBi2Se3 unveiled here is accompanied by a nematicity in the macroscopically coherent odd-parity wavefunction. In this respect, it is clearly distinct from any known nematic states realized in liquid crystals or in non-SC electrons. In the future, it would be interesting to investigate the unusual consequences of odd-parity nematic SC ordering, such as unusual quantization phenomena associated with topological defects or new collective modes arising from the nematic order parameter.

Note added in proof: We notice that a report on two-fold symmetric behaviour in resistivity of a related compound, SrxBi2Se3, appeared on the arXiv server (arXiv:1603.04197; 14 March 2016) shortly after ours (arXiv:1602.08941; 29 February 2016). This work has been recently published24.

Methods

Sample preparation and characterization.

Single crystals of Bi2Se3 were grown by a conventional melt-growth method. Single-crystal samples of CuxBi2Se3 were then obtained by intercalating Cu to single crystals of Bi2Se3 by means of an electrochemical technique25. The value of the Cu content x was determined by the total charge flow during the intercalation process, as well as by the mass change between before and after the intercalation. The crystal axis directions were determined from Laue photos before the intercalation. The onset Tc was checked by using a superconducting quantum interference device (SQUID) magnetometer (MPMS, Quantum Design). After this process, the samples were stored in vacuum until they were mounted to the calorimeter. In the present study, we used three samples, which are labelled Samples #1, #2 and #3. All samples are single crystals of rectangular shapes with x ≃ 0.3. The characteristics of each sample are listed in Supplementary Table 1.

Specific-heat measurement.

We used a 3He-4He dilution refrigerator (Kelvinox 25, Oxford Instruments) to cool down the samples. We performed specific-heat measurement in the temperature range 0.09 K ≤ T ≤ 4 K. We constructed a custom-made high-resolution calorimeter26, shown in Supplementary Fig. 1a. In our calorimeter, a sample was sandwiched between a thermometer and a heater, both of which were made using RuO2 chip resistors. We mounted a sample inside a glove box with an Ar atmosphere. We measured the specific heat by using the a.c. method27: we applied an a.c. current to the heater using a current source (6221, Keithley Instruments), and measured the resultant temperature modulation amplitude Tac and the phase shift φac using lock-in amplifiers (SR830, Stanford Research Systems). The offset sample temperature T was also recorded by another lock-in amplifier. An excitation current to the thermometer was applied using another current source. For most of the data, the raw heat capacity Craw was then obtained as Craw = [P/(2ωHTac)]sinφac, where P is the a.c. heat flow produced by the heater and ωH is the frequency of the heater current. Multiplication by the factor sinφac allows for more accurate evaluation of the heat capacity, even for smaller frequencies28. Notice that the frequency of the temperature oscillation is two times higher than ωH. We typically used ωH = 1.3 Hz and Tac/T ∼ 1.5–2.0% for measurements. For the temperature dependence of C/T below 0.6 K and at zero field (Supplementary Fig. 2), we evaluated Craw by another method to improve the accuracy: we measured the ωH dependence of Tac and fitted Tac(ωH) with the function Tac(ωH) = [P/(4ωHCraw)][1 + (2ωHτ1)2 + (2ωHτ2)−2]−1/2 to obtain Craw, where τ1 and τ2 are the external and internal relaxation times, respectively. The heat capacity of the sample stage (addenda) was measured separately by using a piece of pure silver as a reference sample, and subtracted from the total heat capacity to extract the sample contribution. The addenda contribution is typically 10–20% of the total heat capacity. We confirmed that the addenda does not produce detectable changes in either the θ or φ dependences.

Magnetic-field control.

We applied the magnetic field using a vector-magnet system19, which consists of two orthogonal superconducting solenoids (pointing in the vertical and horizontal directions, respectively) and a rotation stage, as schematically shown in Supplementary Fig. 1c. Within the laboratory frame, we can rotate the magnetic field both vertically, by changing the relative field strengths of the two orthogonal solenoids, and horizontally, by using the horizontal rotation stage. For the vertical rotation, the magnetic field of the solenoids can be controlled with a resolution of 0.1 mT, which results in an angular resolution of 0.006° at 1 T and 0.06° at 0.1 T. The horizontal rotator has an angular resolution of 0.001°, with negligible backlash. Thus, this system allows for a precise two-axis control of the field direction. The directions of the crystalline axes with respect to the laboratory frame are determined by making use of the anisotropy in Hc2. Once the directions of the crystalline axes are determined, we can rotate the magnetic field within the sample frame with the aid of our automation software. All field angle values presented in this Letter are defined in the sample frame. The precision and accuracy of the field alignment are approximately 1°. Notice that this is worse than those achieved for more anisotropic superconductors such as Sr2RuO4 (ref. 26), because of the relatively small out-of-plane Hc2 anisotropy of CuxBi2Se3 (see Supplementary Note 11). Nevertheless, this small anisotropy of CuxBi2Se3 in turn makes the misalignment effect rather small, as explained in Supplementary Note 3.

Theoretical calculation.

The field-angle-dependent heat capacity is calculated on the basis of the Kramer–Pesch approximation, which is appropriate in a low-magnetic-field region29. By using the quasiclassical framework, a Dirac Bogoliubov-de Gennes (BdG) Hamiltonian which describes a topological superconductivity with point nodes derived from the first-principle calculations is reduced to a BdG Hamiltonian for spin-triplet p-wave superconductivity. The corresponding d-vector is d(kF) = (vFz sinφN, −vFz cosφN, vFy cosφN − vFx sinφN). For this state, point nodes are located in the φN-direction on the ab-plane30. Here, we consider a three-dimensional spherical Fermi surface. In the case of a fully gapped order parameter with gap minima, we consider the gap |Δ(k)| = |d(kF)| (1 − r) + |d|maxr, where |d|max is the maximal value of |d(kF)| and r (0 < r < 1) corresponds to the ratio between the minimal and maximal values of |Δ(kF)|. We also performed calculations for a Q2D Fermi surface. We used a Q2D tight-binding model for the normal-state electronic band17 and assumed a point-nodal gap31, as schematically shown in the inset of Supplementary Fig. 6c.

Data availability.

Data supporting the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.