Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Topological boundary modes in isostatic lattices

Nature Physics volume 10, pages 39–45 (2014)Cite this article

Subjects

Abstract

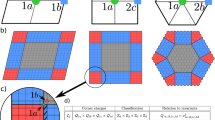
Frames, or lattices consisting of mass points connected by rigid bonds or central-force springs, are important model constructs that have applications in such diverse fields as structural engineering, architecture and materials science. The difference between the number of bonds and the number of degrees of freedom in these lattices determines the number of their zero-frequency ‘floppy modes’. When these are balanced, the system is on the verge of mechanical instability and is termed isostatic. It has recently been shown that certain extended isostatic lattices exhibit floppy modes localized at their boundary. These boundary modes are insensitive to local perturbations, and seem to have a topological origin, reminiscent of the protected electronic boundary modes that occur in the quantum Hall effect and in topological insulators. Here, we establish the connection between the topological mechanical modes and the topological band theory of electronic systems, and we predict the existence of new topological bulk mechanical phases with distinct boundary modes. We introduce one- and two- dimensional model systems that exemplify this phenomenon.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: 1D SSH and isostatic lattice models.
Figure 2: Deformed kagome lattice model.
Figure 3: Zero modes at domain walls.
Figure 4: Zero modes at the edge.

Similar content being viewed by others

References

  1. Phillips, J. C. Topology of covalent non-crystalline solids 2. medium-range order in chalcogenide alloys and α-Si((Ge). J. Non-Cryst. Solids 43, 37–77 (1981).

    Article  ADS  Google Scholar 

  2. Thorpe, M. F. Continuous deformations in random networks. J. Non-Cryst. Solids 57, 355–370 (1983).

    Article  ADS  Google Scholar 

  3. Feng, S. & Sen, P. N. Percolation on elastic networks—new exponent and threshold. Phys. Rev. Lett. 52, 216–219 (1984).

    Article  ADS  Google Scholar 

  4. Jacobs, D. J. & Thorpe, M. F. Generic rigidity percolation—the pebble game. Phys. Rev. Lett. 75, 4051–4054 (1995).

    Article  ADS  Google Scholar 

  5. Liu, A. J. & Nagel, S. R. Nonlinear dynamics—Jamming is not just cool any more. Nature 396, 21–22 (1998).

    Article  ADS  Google Scholar 

  6. Liu, A. J. & Nagel, S. R. Granular and jammed materials. Soft Matter 6, 2869–2870 (2010).

    Article  ADS  Google Scholar 

  7. Liu, A. J. & Nagel, S. R. The jamming transition and the marginally jammed solid. Annu. Rev. Condens. Matter Phys. 1, 347–369 (2010).

    Article  ADS  Google Scholar 

  8. Torquato, S. & Stillinger, F. H. Jammed hard-particle packings: From Kepler to Bernal and beyond. Rev. Mod. Phys. 82, 2633–2672 (2010).

    Article  ADS  Google Scholar 

  9. Wyart, M., Nagel, S. R. & Witten, T. A. Geometric origin of excess low-frequency vibrational modes in weakly connected amorphous solids. Europhys. Lett. 72, 486–492 (2005).

    Article  ADS  Google Scholar 

  10. Wyart, M. On the rigidity of amorphous solids. Ann. De Phys. 30, 1–96 (2005).

    Article  Google Scholar 

  11. Wilhelm, J. & Frey, E. Elasticity of stiff polymer networks. Phys. Rev. Lett. 91, 108103 (2003).

    Article  ADS  Google Scholar 

  12. Heussinger, C. & Frey, E. Floppy modes and nonaffine deformations in random fibre networks. Phys. Rev. Lett. 97, 105501 (2006).

    Article  ADS  Google Scholar 

  13. Huisman, L. & Lubensky, T. C. Internal stresses, normal modes and non-affinity in three-dimensional biopolymer networks. Phys. Rev. Lett. 106, 088301 (2011).

    Article  ADS  Google Scholar 

  14. Broedersz, C., Mao, X., Lubensky, T. C. & MacKintosh, F. C. Criticality and isostaticity in fibre networks. Nature Phys. 7, 983–988 (2011).

    Article  ADS  Google Scholar 

  15. Souslov, A., Liu, A. J. & Lubensky, T. C. Elasticity and response in nearly isostatic periodic lattices. Phys. Rev. Lett. 103, 205503 (2009).

    Article  ADS  Google Scholar 

  16. Mao, X. M., Xu, N. & Lubensky, T. C. Soft modes and elasticity of nearly isostatic lattices: Randomness and dissipation. Phys. Rev. Lett. 104, 085504 (2010).

    Article  ADS  Google Scholar 

  17. Mao, X. M. & Lubensky, T. C. Coherent potential approximation of random nearly isostatic kagome lattice. Phys. Rev. E 83, 011111 (2011).

    Article  ADS  Google Scholar 

  18. Mao, X. M., Stenull, O. & Lubensky, T. C. Elasticity of a filamentous kagome lattice. Phys. Rev. E 87, 042602 (2013).

    Article  ADS  Google Scholar 

  19. Kapko, V., Treacy, M. M. J., Thorpe, M. F. & Guest, S. D. On the collapse of locally isostatic networks. Proc. R. Soc. A 465, 3517–3530 (2009).

    Article  ADS  MathSciNet  Google Scholar 

  20. Maxwell, J. C. On the calculaton of the equilibrium stiffness of frames. Phil. Mag. 27, 294–299 (1865).

    Article  Google Scholar 

  21. Calladine, C. R. Buckminster Fuller’s ‘tensegrity’ structures and clerk Maxwell’s rules for the construction of stiff frames. Int. J. Solids Struct. 14, 161–172 (1978).

    Article  Google Scholar 

  22. Sun, K., Mao, X. & Lubensky, T. C. Surface phonons, elastic response, and conformal invariance in twisted kagome lattices. Proc. Natl Acad. Sci. USA 109, 12369–12374 (2012).

    Article  ADS  Google Scholar 

  23. Halperin, B. I. Quantized hall conductance, current-carrying edge states, and the existence of extended states in a two-dimensional disordered potential. Phys. Rev. B 25, 2185–2190 (1982).

    Article  ADS  Google Scholar 

  24. Haldane, F. D. M. Model for a quantum hall effect without landau levels—condensed matter realization of the parity anomaly. Phys. Rev. Lett. 61, 2015–2018 (1988).

    Article  ADS  MathSciNet  Google Scholar 

  25. Kane, C. L. & Mele, E. J. Z(2) topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).

    Article  ADS  Google Scholar 

  26. Bernevig, B. A., Hughes, T. L. & Zhang, S-C. Quantum spin hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).

    Article  ADS  Google Scholar 

  27. Moore, J. E. & Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 75, 121306 (2007).

    Article  ADS  Google Scholar 

  28. Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).

    Article  ADS  Google Scholar 

  29. Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).

    Article  ADS  Google Scholar 

  30. Qi, X-L. & Zhang, S-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).

    Article  ADS  Google Scholar 

  31. Su, W. P., Schrieffer, J. R. & Heeger, A. J. Solitons in polyacetalene. Phys. Rev. Lett. 42, 1698 (1979).

    Article  ADS  Google Scholar 

  32. Nakahara, M. Geometry, Topology and Physics (Hilger, 1990).

    Book  Google Scholar 

  33. Dirac, P. A. M. The quantum theory of the electron. R. Soc. Lond. Proc. A 117, 610–624 (1928).

    Article  ADS  Google Scholar 

  34. Witten, E. Dynamical breaking of supersymmetry. Nucl. Phys. B 188, 513–554 (1981).

    Article  ADS  Google Scholar 

  35. Cooper, F., Khare, A. & Sukhatme, U. Supersymmetry and quantum mechanics. Phys. Rep. 251, 267–385 (1995).

    Article  ADS  MathSciNet  Google Scholar 

  36. Schnyder, A. P., Ryu, S., Furusaki, A. & Ludwig, A. W. W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008).

    Article  ADS  Google Scholar 

  37. Jackiw, R. & Rebbi, C. Solitons with fermion number 1/2. Phys. Rev. D 13, 3398–3409 (1976).

    Article  ADS  MathSciNet  Google Scholar 

  38. Volovik, G. E. The Universe in a Helium Droplet (Clarenden, 2003).

    MATH  Google Scholar 

  39. Haldane, F. D. M. & Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 100, 013904 (2008).

    Article  ADS  Google Scholar 

  40. Wang, Z., Chong, Y. D., Joannopoulos, J. D. & Soljačić, M. Reflection-free one-way edge modes in a gyromagnetic photonic crystal. Phys. Rev. Lett. 100, 013905 (2008).

    Article  ADS  Google Scholar 

  41. Prodan, E. & Prodan, C. Topological phonon modes and their role in dynamic instability of microtubules. Phys. Rev. Lett. 103, 248101 (2009).

    Article  ADS  Google Scholar 

  42. Berg, N., Joel, K., Koolyk, M. & Prodan, E. Topological phonon modes in filamentary structures. Phys. Rev. E 83, 021913 (2011).

    Article  ADS  Google Scholar 

  43. Callias, C. Axial anomalies and index theorems on open spaces. Commun. Math. Phys. 62, 213–234 (1978).

    Article  ADS  MathSciNet  Google Scholar 

  44. Bott, R. & Seeley, R. Some remarks on paper of callias. Commun. Math. Phys. 62, 235–245 (1978).

    Article  ADS  Google Scholar 

  45. Hirayama, M. & Torii, T. fermion fractionalization and index theorem. Prog. Theor. Phys. 68, 1354–1364 (1982).

    Article  ADS  MathSciNet  Google Scholar 

  46. Niemi, A. J. & Semenoff, G. W. fermion number fractionalization in quantum field theory. Phys. Rep. 135, 99–193 (1986).

    Article  ADS  MathSciNet  Google Scholar 

  47. Lakes, R. Foam structures with a negative Poisson’s ratio. Science 235, 1038–1040 (1987).

    Article  ADS  Google Scholar 

  48. Lawler, M. J. Emergent gauge dynamics of highly frustrated magnets. New J. Phys. 15, 043043 (2013).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

T.C.L. is grateful for the hospitality of the Newton Institute, where some of this work was carried out. This work was supported in part by a Simons Investigator award to C.L.K. from the Simons Foundation and by the National Science Foundation under DMR-1104707 (T.C.L.) and DMR-0906175 (C.L.K.).

Author information

Authors and Affiliations

  1. Department of Physics and Astronomy, University of Pennsylvania, Philadelphia, Pennsylvania 19104, USA

    C. L. Kane & T. C. Lubensky

Authors
  1. C. L. Kane
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. C. Lubensky
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

C.L.K. and T.C.L. contributed to the formulation of the problem, theoretical calculations, and the preparation of the manuscript.

Corresponding author

Correspondence to T. C. Lubensky.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 417 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kane, C., Lubensky, T. Topological boundary modes in isostatic lattices. Nature Phys 10, 39–45 (2014). https://doi.org/10.1038/nphys2835

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphys2835

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing