Main

The average temporal avalanche shape has been measured for earthquakes6 and for dislocation avalanches in plastically deformed metals7,8, but the primary experimental and theoretical focus has always been Barkhausen avalanches in magnetic systems5,6,9,10,11. Theory and experiment agreed well for avalanche sizes and durations, but the strikingly asymmetric shapes found experimentally in ribbons11 disagreed sharply with the theoretical predictions, for which the asymmetry in the scaling shapes under time reversal was at most very small4,6. (We note that the relevant models are not microscopically time-reversal invariant; temporal symmetry is thus emergent.) Doubts about universality4 were resolved when eddy currents were shown to be responsible for the asymmetry, at least on short timescales12, but the exact form of the asymptotic universal scaling function of the Barkhausen avalanche shape still remained elusive.

Here, we report an experimental study of Barkhausen noise in permalloy thin films, where a careful study of the average avalanche shapes leads to symmetric shapes, undistorted by eddy currents (which are suppressed by the sample geometry). We provide a quantitative explanation of the experimental results by solving exactly the mean-field theories for two general models of magnetic reversal: a domain-wall dynamics model13 and the random-field Ising model14. The two mean-field theories are shown to be equivalent, and allow us to compute the average temporal avalanche shape as a function of typical experimental control parameters such as the field rate and the demagnetizing factor.

The relevant statistical information encoded in the Barkhausen noise could in principle be derived from the joint two-point time-velocity distribution Gc,k(V,t;V ′,t+Δ), yielding the conditional probability that the noise at time t+Δ is equal to V ′ if it was equal to V at time t. Here, c is the external field rate and k the demagnetizing factor. The standard avalanche distributions can be derived from this parent distribution; for example the duration distribution is given by

The renormalization group makes use of an emergent scale invariance for Barkhausen noise. Here, the two-point time-velocity distribution, when coarse-grained in time by a factor b and rescaled downwards in velocity by a factor bx, rescales at long durations to itself:

where is the rescaled field rate, the rescaled demagnetizing factor and x,y,w are universal scaling exponents. Repeating n rescalings until Δ/bn=1, leads to a universal scaling form

where is a universal multivariable scaling function and c0 and k0 are the small scale values of the field rate and demagnetizing factor, respectively.

Universal scale invariant forms can then be derived for all statistical quantities of interest, including the temporal average shape. For avalanches of duration T, the average shape is defined as the average velocity for avalanches that begin and end at V =0 in a duration T. It has an associated universal scaling form,

where is a universal scaling function, dependent on the rescaled time λ≡Δ/T, the rescaled demagnetizing factor K≡(k/k0)Tw, and the driving field C≡(c/c0)Ty. It is universal in the sense that in the scaling regime it does not depend on microscopic features of the material, so long as the system is at a critical point.

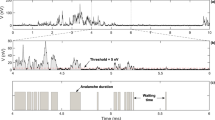
We record the Barkhausen noise by a standard inductive technique on a 1-μm-thick permalloy film with polycrystalline structure (see Methods section for details on the measurement and sample preparation). The Barkhausen noise is composed of a series of intermittent pulses, due to avalanches in the magnetization, combined with background instrumental noise. In most crackling noise phenomena, avalanches are usually identified by setting a threshold Vth above the background noise. This method works well if the signal to noise ratio is high, but can induce spurious effects otherwise15. Our thin films have a correspondingly weak signal, thus making the use of Vth inappropriate. In addition, the measurement apparatus has a response function that distorts the original pulses. We instead extract the pulses using Wiener deconvolution16, which optimally filters the background noise and avoids the use of thresholds (see Fig. 1).

Figure 1: Extracting average shapes from noisy data by Wiener deconvolution.
figure 1

Time-series data (jagged line) are traditionally separated into avalanches using a threshold Vth set above the instrumental noise (dotted blue line)—here breaking one avalanche into a few pieces. We instead do an optimal Wiener deconvolution (smoothed red curve, see text), allowing the use of a zero threshold (solid black line), which avoids distortions of the average shape and also gives more decades of size and duration scaling. Averaging over all avalanches with this duration gives us 〈V (t,T)〉 (dashed green curve).

Full size image

The universality class of the Barkhausen noise in a sample is usually identified by measuring the voltage distribution, the power spectrum and the distributions of avalanche sizes S and durations T (ref. 17; Fig. 2). Notice the striking agreement between data and simulations (roughly matched in number of avalanches), including two well-known predictions: the (unusual) rate-dependent critical exponents in Fig. 2a,b,d, and the crossover in 〈S〉 versus T due to the demagnetization factor in Fig. 2c (not before seen in the mean-field universality class5, presumably hidden by eddy-current effects). Notice that in Fig. 2a,b,d these are three-variable scaling functions, although in the first two cases no analytical form is known. The remaining small discrepancies have experimental explanations: the weak dependence of the demagnetizing factor k on the rate is plausibly due to changing experimental conditions, the rate-driven vertical shifts in Fig. 2c are due to the presence of instrumental noise, and the deviations in Fig. 2d are at voltages below the instrumental noise level of 18 nV.

Figure 2: Multivariable scaling; experiment (symbols) versus ABBM mean-field theory (lines), at different sweep frequencies Ω.
figure 2

a,b, For the distributions of avalanche sizes S (a) and of durations T (b), we confirm c∼Ω, and k approximately constant (see insets, and also equation (2)), as theoretically expected. Note the rate-dependent critical exponents P(S)∼S−(3/2−c/2), and P(T)∼T−(2−c). The error bars in the insets of a,b are estimated errors of the best-fit parameters c and k based on random sampling around the best fit. (Vertical scales are shifted towards higher values for clarity.) c, The mean avalanche size 〈S〉∼Tx+1=T2 below the demagnetization cutoff and ∼T above it, and the power spectrum for Ω=0.05 Hz goes as ω−(x+1)=ω−2 (inset). d, The distribution of voltages P(V |k,c)∝Vc−1exp(−k V). Note that a,b and d are three-variable scaling forms. The error bars have been calculated by using the bootstrap method, with random replacement of entire magnetization cycles.

Full size image

Finally, we focus on the measurement of the average temporal avalanche shape, considering all the avalanches of a given duration T and averaging the voltage signal at each time step t. (In practice, we average the avalanches using duration bins centred at T and with geometrically increasing sizes.) Figure 3a shows the resulting nearly symmetric temporal average avalanche shape, which starts out as a parabola and then flattens as the duration of the avalanche increases (see Fig. 3c).

Figure 3: Experiment and theory: average shapes and scaling.
figure 3

a, The temporal average avalanche shape for different avalanche durations T, rescaled to unit height and duration. Notice the symmetric, parabolic shape for short durations, and the flattening for longer durations. b, Mean-field calculation for the average shape including a demagnetizing factor k as in equation (1). The shape is an inverted parabola, 4t/T(1−t/T), for short durations and flattens at long durations. Here, k is 0.05 μs−1, slightly different from the value used in Fig. 2. c,d, Deviations from the inverted parabola. Note the quantitative agreement between experiment and theory. The error bars have been calculated by using the bootstrap method, with random replacement of entire magnetization cycles.

Full size image

It has been argued that dipolar magnetic fields are sufficiently long-ranged that mean-field theory should be quantitatively applicable in three-dimensional samples18. Similar considerations apply to many of the systems exhibiting crackling noise, such as dislocation-mediated plasticity19 and earthquakes20 where long-range interactions are provided by elastic strains. Our films are thinner than polycrystalline ribbons known to exhibit mean-field behaviour17, but thicker than previously studied two-dimensional films21. The classic mean-field theory for domain-wall depinning is the single-degree of freedom ABBM model13, which treats the domain wall as a rigid object at position X(t), advancing in a random pinning field statistically chosen as a random walk in X,

with 〈W(X)〉=0 and 〈W(X)W(X′)〉=|X−X′| (Brownian noise). The ABBM model predicts that the avalanche size and duration distributions decay as power laws with rate-dependent exponents10. The exact form of the scaling functions for these distributions, including the cutoff to the power-law behaviour, can be computed in the limit c=0 (ref. 10). To compare with experiments for c>0, we resort to numerical integration of equation (1), obtaining close agreement, as shown in Fig. 2.

The average avalanche shape in the ABBM model has not been extensively explored numerically, but an approximate analytical calculation10,22 gave a lobe of a sinusoid . In that calculation, the approximation 〈V (X(t),T)〉≃V (〈X(t)〉,T)〉 was made. (That is, the fluctuations in the growth of the avalanche size with time were neglected, leading to a slight distortion of the predicted temporal average avalanche shape.) We avoid this approximation by using a transformation23,24 to a time-dependent noise with a variance proportional to the avalanche velocity V (ξ(t) has unit variance)

which can be solved in the Stratonovich interpretation in the limit c=0, k=0. After defining a new variable Y =V1/2, we have a stochastic equation that we may solve explicitly. Using the resulting probability for the first return to the origin, we calculate the temporal shape10,25 (see Supplementary Information):

where in the future we will use t instead of Δ to denote the time elapsed from the beginning of the avalanche. We have numerically verified that the average shape is indeed an inverted parabola (and not the lobe of a sine wave10).

Interestingly, an inverted parabola was reported6,9 in numerical studies of the (nucleated) random-field Ising model in the mean-field limit (the ‘shell’ model)14. Front depinning and nucleated transitions have different upper critical dimensions and different short-range critical exponents, and it was conceivable that their mean-field theories had different average shapes, albeit sharing critical exponents.

On closer examination, these two models are the same in the continuum limit. The shell model has a set of interacting spins Mi=±1 with random fields hi distributed by a Gaussian, interacting with a strength J/N with all other spins; each spin flips when the net field it feels, , is positive. Here, H(t)=H0+c t is the external field, increasing with rate c, and the spin feels the magnetization through both the infinite-range coupling J/N and the demagnetizing factor k. A shell-model avalanche proceeds in parallel, with a shell of Vn unstable spins flipping at the n-th time-step, then triggering a new set of spins Vn+1 to flip:

where P is the Poisson distribution for the set of spins Vn+1 to be included in the range {f,f+2J Vn}. For large V, we may approximate the Poisson distribution as a Gaussian , leading to , which is clearly a discretized version of equation (2), where is the distance to the critical threshold. This equivalence, in retrospect, provides an alternative explanation for the origin of Brownian noise statistics for the ABBM domain-wall potential18.

Finally, we consider the effects of the two main physical perturbations, the driving field c and the demagnetizing factor k. The transformed equation (2) now takes the form

Under rescaling , tt/b, and for uncorrelated Gaussian white noise, we have ξb1/2ξ. By balancing the noise with the left-hand side, we find x=1; thus the driving field is marginal (y=0), and the demagnetizing factor is relevant, with scaling dimension w=1. The demagnetizing factor k sets the characteristic maximum of the avalanche size and duration. The two-point probability function in the case c=0 can be found exactly26 and the functional form of the resulting shape is

and hence the scaling function is

Intuitively, the form of the scaling function leads to a flattening of the average shape at long times because k acts to cap the velocities.

As can be seen in Fig. 3, this behaviour is verified by our experiments: the value of k is chosen to be 0.05 μs−1, slightly different from the value used to fit the data shown in Fig. 2; this difference is expected because our analytical form is available only for c=0; simulations at c,k given in the insets of Fig. 2a and b respectively, yield good, albeit noisy, agreement with experiment. Also, the small residual asymmetry remaining is plausibly attributable to amplifier-induced distortions that were not possible to correct for. The impulse response functions of the individual instruments (amplifier, low-pass filter and sensing coils) were measured subsequently to taking the data, and used to deconvolve the resulting signal (see Supplementary Information).

The effect of the driving field c, a marginal field at mean-field, can be calculated exactly at k=0 using a result from ref. 27: for an absorbing boundary condition at V =0, the two-point probability function for the Brownian motion in a logarithmic potential is Gc,k=0(V,t;ε,0)=4/(Γ[1+ν])(4t)−(1+ν)ε2νVe−V2/(4t)(1+O(ε2)), where ν=(1−c)/2. Using this expression, the scaling form is reduced in magnitude but remains parabolic, with .

What lessons can be drawn from our work? The optimal extraction of signal from noise is an understated but remarkably powerful tool in the study of crackling noise. Using such tools, modern experiments that allow simultaneous analysis of multiple properties can provide sharp tests of proposed theories. Finally, universal multiparameter scaling functions are powerful predictive tools in problems with emergent scale invariance, going far beyond power laws: shapes are more informative than slopes.

Methods

Sample preparation and experimental measurements. A 1-μm-thick ferromagnetic film with nominal composition Ni81Fe19 (permalloy) is deposited by magnetron sputtering from a commercial target, on a glass substrate covered by a 2-nm-thick Ta buffer layer. The deposition is carried out with the substrate moving at constant speed through the plasma to improve the film uniformity, with the following parameters: base vacuum of 10−7 torr, deposition pressure of 5.2 mtorr (99.99% pure Ar at 20 sccm constant flow), and 65 W radiofrequency power. The deposition rate of 0.28 nm s−1 is calibrated with X-ray diffraction, which also confirms the polycrystalline character of the film. Quasi-static magnetization curves obtained with a vibrating sample magnetometer indicate isotropic in-plane magnetic properties with an out-of-plane anisotropy contribution, a behaviour related to the stress stored in the film, and to the columnar microstructure28,29,30.

Barkhausen noise time series are obtained using the inductive technique in an open magnetic circuit. The sample has dimensions 10 mm×4 mm. Sample and pickup coils are inserted in a long solenoid with compensation for the effects of the border. The sample is driven by a triangular driving magnetic field with an amplitude high enough to saturate the film (±15 kA m−1). The driving field frequency is varied in the range 0.05–0.4 Hz. Barkhausen noise is detected by a 400-turn sensing coil (3.5 mm long, 4.5 mm wide, 1.25 MHz resonance frequency) wound around the central part of sample. A second pickup coil, with the same cross-section and number of turns, is adapted to compensate the signal induced by the magnetizing field. The Barkhausen signal is then amplified and filtered with a 100 kHz low-pass filter, and data finally acquired at 0.2 and 4 million samples per second. The data at different rates are statistically very similar after Wiener filtering (spurious peaks are present in the high-frequency regime of the spectrum, independently of the rate), with very small differences at short durations and small voltages. Wiener filtering is practically more efficient at large rates, for uncorrelated noise, but the noise amplitude remains larger than at low rates. Thus, the optimal use of this filter depends on the observables studied. For the distributions in Fig. 2, to gain more accuracy at short durations and small avalanche sizes by reducing the noise level, the low rate is used. For the average temporal shapes, in Fig. 3, it being more important to capture variations of the signal at small timescales by a more accurate Wiener filter, the large rate is used. The time series is acquired just around the central part of the hysteresis loop near the coercive field, where the domain-wall motion is the main magnetization mechanism24. By using a thin film, we have removed the confounding effects of eddy currents, whose timescale12 for the present sample is estimated to be Tp∼0.04 μs, much smaller than the avalanche durations studied.

Data analysis. To address the low signal from the thin film, we analyse the data by using Wiener deconvolution16. The output signal is assumed to be of the form , where h(t) denotes the impulse response function, V (t) the original microscopic signal, and n(t) the background noise. Given an estimated impulse response Fourier series , an estimated deconvolved noise power spectrum and a theoretically expected frequency spectrum for the deconvolved signal , the filtered data V (t) is the inverse Fourier transform of

Here, the impulse function is estimated by measuring the impulse response of the individual instruments composing the apparatus. We note that if the signal has a high resolution, a detailed knowledge of the impulse response function is needed to remove the effect of the instrument. As a signal function, we use a power fit (see also Supplementary Information). To estimate the noise contribution , we measure the power spectrum of the instrumental noise, recorded without the material, maximizing over several runs. The Wiener deconvolution, shown in Fig. 1 and in the inset of Fig. 2c, smoothens the signal and removes spurious high-frequency oscillations due to the amplifier and filters used in the experiments. Importantly, this procedure also allows us to avoid the use of thresholds for defining the temporal extent of the avalanches, improving our estimates for both the scaling exponents and the average avalanche shapes.