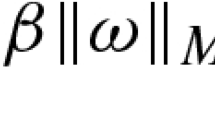Abstract
Let \(I^d \)be the d‐dimensional cube, \(I^d = [0,1]^d \), and let \(F \ni f \mapsto Sf \in L_\infty (I^d ) \)be a linear operator acting on the Sobolev space F, where Fis either
or
where
We assume that the problem elements fsatisfy the condition \(\sum\nolimits_{\left| m \right| = r} {{\text{esssup}}} _{x \in I^d } \left| {f^{(m)} (x)} \right| \leqslant 1 \)and that Sis continuous with respect to the supremum norm.
We study sensitivity of optimal recovery of Sfrom inexact samples of ftaken at npoints forming a uniform grid on \(I^d \). We assume that the inaccuracy in reading the sample vector is measured in the pth norm and bounded by a nonnegative number δ. The sensitivity is defined by the difference between the optimal errors corresponding to the exact and perturbed readings, respectively. Our main result is that this difference is bounded by \(\mathcal{A}\delta \), where \(\mathcal{A} \)is a positive constant independent of the number of samples. This indicates that the curse of dimension, which badly affects the optimal errors, does not extend to sensitivity.
Similar content being viewed by others
References
R. Abgrall and T. Sonar, On the use of Mühlbach expansions in the recovery step of ENO methods, Numer. Math. 76(1) (1997) 1-25.
S. Amat, F. Aràndiga, A. Cohen and R. Donat, Tensor product multiresolution analysis with error control, Technical Report GrAN-99-4, Department de Matemàtica Aplicada, University of València (1999).
F. Aràndiga, R. Donat and A. Harten, Multiresolution based on weighted averages of the hat function I: Linear reconstruction operators, SIAM J. Numer. Anal. 36(1) (1999) 160-203.
F. Aràndiga, R. Donat and A. Harten, Multiresolution based on weighted averages of the hat function II: Nonlinear reconstruction operators, SIAM J. Sci. Comput. 20(3) (1999) 1053-1093.
A. Cohen, I. Daubechies and J. Feauveau, Biorthogonal bases of compactly supported wavelets, Comm. Pure Appl. Math. 45 (1992) 485-560.
R. Donat, Studies on error propagation for certain nonlinear approximations to hyperbolic equations: Discontinuities in derivative, SIAM J. Numer. Anal. 31 (1994) 655-679.
M. Guichaoua, Analyses multiréolution biorthogonales associés àla réolution d'éuations aux derivés partielles, Ph.D. thesis, Ecole Supéieure de Méanique de Marseille, Universitéde la Mediterrané Aix-Marseille II (1999).
A. Harten, ENO schemes with subcell resolution, J. Comput. Phys. 83 (1989) 148-184.
A. Harten, Discrete multiresolution analysis and generalized wavelets, J. Appl. Numer. Math. 12 (1993) 153-192.
A. Harten, Multiresolution representation of data II: General framework, SIAM J. Numer. Anal. 33 (1996) 1205-1256.
A. Harten, B. Engquist, S. Osher and S. Chakravarthy, Uniformly high order accurate essentially non-oscillatory schemes III, J. Comput. Phys. 71 (1987) 231-303.
A. Harten and I. Yad-Shalom, Fast multiresolution algorithms for matrix-vector multiplication, SIAM J. Numer. Anal. 371 (1994) 1191-1218.
W. Sweldens, The lifting scheme: a customer-design construction of biorthogonal wavelets, Appl. Comput. Harmon. Anal. 3(2) (1996) 186-200.
W. Sweldens, The lifting scheme: a construction of second generation wavelets, SIAM J. Math. Anal. 29(2) (1998) 511-546 (electronic).
Rights and permissions
About this article
Cite this article
Kowalski, M.A. Sensitivity of best recovery in the Sobolev spaces \(W_\infty ^{r,d} \), \(\widetilde W_\infty ^{r,d}\)for perturbed sampling. Numerical Algorithms 23, 251–261 (2000). https://doi.org/10.1023/A:1019152001173
Issue Date:
DOI: https://doi.org/10.1023/A:1019152001173