Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-05-24T07:32:13.200Z Has data issue: false hasContentIssue false
  • English
  • Français

IDEAL PROJECTIONS AND FORCING PROJECTIONS

Published online by Cambridge University Press:  12 December 2014

SEAN COX  and
MARTIN ZEMAN
SEAN COX
Affiliation:
DEPARTMENT OF MATHEMATICS AND APPLIED MATHEMATICS VIRGINIA COMMONWEALTH UNIVERSITY 1015 FLOYD AVENUE RICHMOND, VIRGINIA 23284, USAE-mail: scox9@vcu.edu
MARTIN ZEMAN
Affiliation:
DEPARTMENT OF MATHEMATICS 340 ROWLAND HALL UNIVERSITY OF CALIFORNIA, IRVINE IRVINE, CA 92697-3875, USAE-mail: mzeman@math.uci.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well known that saturation of ideals is closely related to the “antichain-catching” phenomenon from Foreman–Magidor–Shelah [10]. We consider several antichain-catching properties that are weaker than saturation, and prove:

  1. (1) If 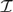${\cal I}$ is a normal ideal on 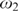$\omega _2 $ which satisfies stationary antichain catching, then there is an inner model with a Woodin cardinal;

  2. (2) For any 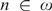$n \in \omega $, it is consistent relative to large cardinals that there is a normal ideal 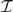${\cal I}$ on 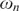$\omega _n $ which satisfies projective antichain catching, yet 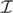${\cal I}$ is not saturated (or even strong). This provides a negative answer to Open Question number 13 from Foreman’s chapter in the Handbook of Set Theory ([7]).

Type
Articles
Information
The Journal of Symbolic Logic , Volume 79 , Issue 4 , December 2014 , pp. 1247 - 1285
Copyright
Copyright © The Association for Symbolic Logic 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Balcar, B. and Franek, F., Completion of factor algebras of ideals, Proceedings of the American Mathematical Society, vol. 100 (1987), no. 2, pp. 205–212.CrossRefGoogle Scholar
Baumgartner, James E. and Taylor, Alan D., Saturation properties of ideals in generic extensions. II, Transactions of the American Mathematical Society, vol. 271 (1982), no. 2, pp. 587–609.Google Scholar
Burke, Douglas R., Precipitous towers of normal filters, this JOURNAL, vol. 62 (1997), no. 3, pp. 741–754.Google Scholar
Claverie, Benjamin and Schindler, Ralf, Woodin’s axiom (*), bounded forcing axioms, and precipitous ideals on ω 1, this JOURNAL, vol. 77 (2012), no. 2, pp. 475–498.Google Scholar
Cox, Sean, PFA and ideals on ω 2whose associated forcings are proper, Notre Dame Journal of Formal Logic, vol. 53 (2012), no. 3, pp. 397–412.Google Scholar
Cummings, James, Iterated forcing and elementary embeddings, Handbook of set theory, vols. 1–3, Springer, Dordrecht, 2010, pp. 775–883.CrossRefGoogle Scholar
Foreman, Matthew, Ideals and Generic Elementary Embeddings, Handbook of set theory, Springer, Dordrecht, 2010.CrossRefGoogle Scholar
Foreman, Matthew and Komjath, Peter, The club guessing ideal: Commentary on a theorem of Gitik and Shelah, Journal of Mathematical Logic, vol. 5 (2005), no. 1, pp. 99–147.CrossRefGoogle Scholar
Foreman, Matthew and Magidor, Menachem, Large cardinals and definable counterexamples to the continuum hypothesis, Annals of Pure and Applied Logic, vol. 76 (1995), no. 1, pp. 47–97.CrossRefGoogle Scholar
Foreman, M., Magidor, M., and Shelah, S., Martin’s maximum, saturated ideals, and nonregular ultrafilters. I, Annals of Mathematics, second series, vol. 127 (1988), no. 1, pp. 1–47.Google Scholar
Foreman, M., Magidor, M., and Shelah, S., Martin’s maximum, saturated ideals and nonregular ultrafilters. II, Annals of Mathematics, second series, vol. 127 (1988), no. 3, pp. 521–545.CrossRefGoogle Scholar
Gitik, Moti, The nonstationary ideal on ℵ2, Israel Journal of Mathematics, vol. 48 (1984), no. 4, pp. 257–288.CrossRefGoogle Scholar
Gitik, Moti and Shelah, Saharon, Forcings with ideals and simple forcing notions, Israel Journal of Mathematics, vol. 68 (1989), no. 2, pp. 129–160.CrossRefGoogle Scholar
Jech, Thomas, Set theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Jech, T., Magidor, M., Mitchell, W., and Prikry, K., Precipitous ideals, this JOURNAL, vol. 45 (1980), no. 1, pp. 1–8.Google Scholar
Kanamori, Akihiro, The higher infinite, 2nd ed., Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Ketchersid, Richard, Larson, Paul, and Zapletal, JindŘich, Increasing δ ½ and Namba-style forcing, this Journal, vol. 72 (2007), no. 4, pp. 1372–1378.Google Scholar
Larson, Paul B., The stationary tower, University Lecture Series, vol. 32, American Mathematical Society, Providence, RI, 2004. Notes on a course by W. Hugh Woodin.Google Scholar
Mitchell, W. J. and Schimmerling, E., Weak covering without countable closure, Mathematical Research Letters, vol. 2 (1995), no. 5, pp. 595–609.Google Scholar
Schimmerling, E. and Steel, J. R., The maximality of the core model, Transactions of the American Mathematical Society, vol. 351 (1999), no. 8, pp. 3119–3141.CrossRefGoogle Scholar
Claverie, Benjamin and Schindler, Ralf-Dieter, Woodin’s axiom (*), bounded forcing axioms, and precipitous ideals on ω 1, this JOURNAL, vol. 77 (2012), no. 2, pp. 475–498.Google Scholar
Steel, John R., The core model iterability problem, Lecture Notes in Logic, vol. 8, Springer-Verlag, Berlin, 1996.CrossRefGoogle Scholar
Hugh Woodin, W., The axiom of determinacy, forcing axioms, and the nonstationary ideal, de Gruyter Series in Logic and its Applications, vol. 1, Walter de Gruyter & Co., Berlin, 1999.Google Scholar
Zeman, Martin, Inner models and large cardinals, de Gruyter Series in Logic and its Applications, vol. 5, Walter de Gruyter & Co., Berlin, 2002.Google Scholar