Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-06-10T03:58:41.038Z Has data issue: false hasContentIssue false
  • English
  • Français

Singularity formation on perturbed planar shock waves

Published online by Cambridge University Press:  08 May 2018

W. Mostert Open the ORCID record for W. Mostert [Opens in a new window] ,
D. I. Pullin ,
R. Samtaney  and
V. Wheatley
W. Mostert
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, CA 91125, USA
D. I. Pullin
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, CA 91125, USA
R. Samtaney
Affiliation:
Mechanical Engineering, Physical Sciences and Engineering Division, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia, 23955-6900
V. Wheatley
Affiliation:
School of Mechanical and Mining Engineering, University of Queensland, QLD 4072, Australia
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an analysis that predicts the time to development of a singularity in the shape profile of a spatially periodic perturbed, planar shock wave for ideal gas dynamics. Beginning with a formulation in complex coordinates of Whitham’s approximate model geometrical shock dynamics (GSD), we apply a spectral treatment to derive the asymptotic form for the leading-order behaviour of the shock Fourier coefficients for large mode numbers and time. This is shown to determine a critical time at which the coefficients begin to decay, with respect to mode number, at an algebraic rate with an exponent of 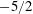$-5/2$ , indicating loss of analyticity and the formation of a singularity in the shock geometry. The critical time is found to be inversely proportional to a representative measure of perturbation amplitude $\unicode[STIX]{x1D716}$ with an explicit analytic form for the constant of proportionality in terms of gas and shock parameters. To leading order, the time to singularity formation is dependent only on the first Fourier mode. Comparison with results of numerical solutions to the full GSD equations shows that the predicted critical time somewhat underestimates the time for shock–shock (triple-point) formation, where the latter is obtained by post-processing the numerical GSD results using an edge-detection algorithm. Aspects of the analysis suggest that the appearance of loss of analyticity in the shock surface may be a precursor to the first appearance of shock–shocks, which may account for part of the discrepancy. The frequency of oscillation of the shock perturbation is accurately predicted. In addition, the analysis is extended to the evolution of a perturbed planar, fast magnetohydrodynamic shock for the case when the external magnetic field is aligned parallel to the unperturbed shock. It is found that, for a strong shock, the presence of the magnetic field produces only a higher-order correction to the GSD equations with the result that the time to loss of analyticity is the same as for the gas-dynamic flow. Limitations and improvements for the analysis are discussed, as are comparisons with the analogous appearance of singularity formation in vortex-sheet evolution in an incompressible inviscid fluid.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 846 , 10 July 2018 , pp. 536 - 562
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chisnell, R. F. 1957 The motion of a shock wave in a channel, with applications to cylindrical and spherical shock waves. J. Fluid Mech. 2, 286–298.Google Scholar
Clavin, P. 2013 Nonlinear analysis of shock–vortex interaction: Mach stem formation. J. Fluid Mech. 721, 324–339.CrossRefGoogle Scholar
Denet, B., Biamino, L., Lodato, G., Vervisch, L. & Clavin, P. 2015 Model equation for the dynamics of wrinkled shockwaves: comparison with DNS and experiments. Combust. Sci. Technol. 187 (1–2), 296–323.Google Scholar
Faria, L. M., Kasimov, A. R. & Rosales, R. R. 2015 Theory of weakly nonlinear self-sustained detonations. J. Fluid Mech. 784, 163–198.Google Scholar
Freeman, N. C. 1957 On the stability of plane shock waves. J. Fluid Mech. 2 (4), 397–411.Google Scholar
Gelb, A. & Tadmor, E. 1999 Detection of edges in spectral data. Appl. Comput. Harmon. Anal. 7, 101–135.Google Scholar
Gelb, A. & Tadmor, E. 2000 Detection of edges in spectral data. Part II. Nonlinear enhancement. SIAM J. Numer. Anal. 38 (4), 1389–1408.Google Scholar
Gelb, A. & Tadmor, E. 2006 Adaptive edge detectors for piecewise smooth data based on the minmod limiter. J. Sci. Comput. 28 (2/3), 279–306.Google Scholar
Henshaw, W. D., Smyth, N. F. & Schwendeman, D. W. 1986 Numerical shock propagation using geometrical shock dynamics. J. Fluid Mech. 171, 519–545.CrossRefGoogle Scholar
Lodato, G., Vervisch, L. & Clavin, P. 2016 Direct numerical simulation of shock wavy-wall interaction: analysis of cellular shock structure and flow patterns. J. Fluid Mech. 789, 221–258.Google Scholar
Lodato, G., Vervisch, L. & Clavin, P. 2017 Numerical study of smoothly perturbed shocks in the Newtonian limit. Flow Turbul. Combust. 99, 887–908.Google Scholar
Majda, A. & Rosales, R. 1983 A theory for spontaneous Mach stem formation in reacting fronts. Part I. The basic perturbation analysis. SIAM J. Appl. Maths 43, 1310–1334.CrossRefGoogle Scholar
Moore, D. W. 1979 The spontaneous appearance of a singularity in the shape of an evolving vortex sheet. Proc. R. Soc. Lond. A 365 (1720), 105–119.Google Scholar
Mostert, W., Pullin, D. I., Samtaney, R. & Wheatley, V. 2017 Geometrical shock dynamics for magnetohydrodynamic fast shocks. J. Fluid Mech. 811, R2.Google Scholar
Olver, F. W. J. 1974 Asymptotics and Special Functions. Academic Press.Google Scholar
Schwendeman, D. W. 1993 A new numerical method for shock wave propagation based on geometrical shock dynamics. Proc. R. Soc. Lond. A 441 (1912), 331–341.Google Scholar
Watanabe, M. & Takayama, K. 1991 Stability of converging cylindrical shock waves. Shock Waves 1 (2), 149–160.CrossRefGoogle Scholar
Wheatley, V., Pullin, D. I. & Samtaney, R. 2005 Regular shock refraction at an oblique planar density interface in magnetohydrodynamics. J. Fluid Mech. 522, 179–214.Google Scholar
Whitham, G. B. 2011 Linear and Nonlinear Waves. Wiley.Google Scholar
Whitham, G. B. 1957 A new approach to problems of shock dynamics. Part I. Two-dimensional problems. J. Fluid Mech. 2, 145–171.Google Scholar