Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-23T07:29:37.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure and location of branch point singularities for Stokes waves on deep water

Published online by Cambridge University Press:  12 July 2016

Pavel M. Lushnikov
Pavel M. Lushnikov*
Affiliation:
Department of Mathematics and Statistics, University of New Mexico, Albuquerque, MSC01 1115, NM 87131, USA
*
†Email address for correspondence: plushnik@math.unm.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The Stokes wave is a finite-amplitude periodic gravity wave propagating with constant velocity in an inviscid fluid. The complex analytical structure of the Stokes wave is analysed using a conformal mapping of a free fluid surface of the Stokes wave onto the real axis with the fluid domain mapped onto the lower complex half-plane. 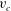There is one square root branch point per spatial period of the Stokes wave located in the upper complex half-plane at a distance $v_{c}$ from the real axis. The increase of Stokes wave height results in 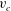$v_{c}$ approaching zero with the limiting Stokes wave formation at 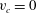$v_{c}=0$. The limiting Stokes wave has a 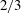$2/3$ power-law singularity forming a 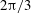$2{\rm\pi}/3$ radians angle on the crest which is qualitatively different from the square root singularity valid for arbitrary small but non-zero 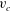$v_{c}$, making the limit of zero 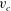$v_{c}$ highly non-trivial. That limit is addressed by crossing a branch cut of a square root into the second and subsequently higher sheets of the Riemann surface to find coupled square root singularities at distances 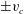$\pm v_{c}$ from the real axis at each sheet. The number of sheets is infinite and the analytical continuation of the Stokes wave into all of these sheets is found together with the series expansion in half-integer powers at singular points within each sheet. It is conjectured that a non-limiting Stokes wave at the leading order consists of an infinite number of nested square root singularities which also implies the existence in the third and higher sheets of additional square root singularities away from the real and imaginary axes. These nested square roots form a 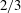$2/3$ power-law singularity of the limiting Stokes wave as 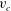$v_{c}$ vanishes.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 800 , 10 August 2016 , pp. 557 - 594
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amick, C. J. & Fraenkel, L. E. 1987 On the behavior near the crest of waves of extreme form. Trans. Am. Math. Soc. 299, 273–298.CrossRefGoogle Scholar
Amick, C. J., Fraenkel, L. E. & Toland, J. F. 1982 On the Stokes conjecture for the wave of extreme form. Acta Math. 148, 193–214.CrossRefGoogle Scholar
Babenko, K. I. 1987 Some remarks on the theory of surface waves of finite amplitude. Sov. Math. Dokl. 35 (3), 599–603.Google Scholar
Buffoni, B., Dancer, E. N. & Toland, J. F. 2000 The sub-harmonic bifurcation of Stokes waves. Arch. Rat. Mech. Anal. 152, 241–271.CrossRefGoogle Scholar
Buffoni, B. & Toland, J. F. 2001 Dual free boundaries for Stokes waves. C. R. Acad. Sci. Paris I 332, 73–78.CrossRefGoogle Scholar
Dyachenko, A. I., Kuznetsov, E. A., Spector, M. & Zakharov, V. E. 1996 Analytical description of the free surface dynamics of an ideal fluid (canonical formalism and conformal mapping). Phys. Lett. A 221, 73–79.CrossRefGoogle Scholar
Dyachenko, S. A., Lushnikov, P. M. & Korotkevich, A. O. 2013a The complex singularity of a Stokes wave. J. Expl Theor. Phys. Lett. 98 (11), 767–771.Google Scholar
Dyachenko, S. A., Lushnikov, P. M. & Korotkevich, A. O.2015a Branch Cuts of Stokes Wave on Deep Water. Part I: numerical Solution and Padé Approximation. arXiv:1507.02784.CrossRefGoogle Scholar
Dyachenko, S. A., Lushnikov, P. M. & Korotkevich, A. O.2015b Library of Stokes waves, http://stokeswave.org.Google Scholar
Dyachenko, S. A., Lushnikov, P. M. & Korotkevich, A. O. 2016 Branch cuts of Stokes wave on deep water. Part I: numerical solution and Padé approximation. Stud. Appl. Maths. doi:101111/sapm.12128.CrossRefGoogle Scholar
Dyachenko, S. A., Lushnikov, P. M. & Vladimirova, N. 2013b Logarithmic scaling of the collapse in the critical Keller–Segel equation. Nonlinearity 26, 3011–3041.CrossRefGoogle Scholar
Fraenkel, L. E. 2007 A constructive existence proof for the extreme Stokes wave. Arch. Rat. Mech. Anal. 183, 187–214.CrossRefGoogle Scholar
Fraenkel, L. E. 2010 The behaviour near the crest of an extreme Stokes wave. Eur. J. Appl. Maths 21, 165–180.CrossRefGoogle Scholar
Fraenkel, L. E. & Harwin, P. J. 2010 On the local uniqueness and the profile of the extreme Stokes wave. Eur. J. Appl. Maths 21, 137–163.CrossRefGoogle Scholar
Golubev, V. V. 1950 Lectures on the Analytic Theory of Differential Equations (in Russian). Gosud. Izd. Techniko-Teor. Leterat.Google Scholar
Grant, M. A. 1973 The singularity at the crest of a finite amplitude progressive Stokes wave. J. Fluid Mech. 59 (2), 257–262.CrossRefGoogle Scholar
Hille, E. 1997 Ordinary Differential Equations in the Complex Domain. Dover.Google Scholar
Ince, E. L. 1956 Ordinary Differential Equations. Dover.Google Scholar
Longuet-Higgins, M. S. & Fox, M. J. H. 1977 Theory of the almost-highest wave: the inner solution. J. Fluid Mech. 80 (4), 721–741.CrossRefGoogle Scholar
Lushnikov, P. M.2015 Branch cuts of Stokes wave on deep water. Part II: structure and location of branch points in infinite set of sheets of Riemann surface. arXiv:1509.03393.Google Scholar
Lushnikov, P. M., Dyachenko, S. A. & Korotkevich, A. O. 2015 Branch cut singularity of Stokes wave on deep water. In Presentation at The Ninth IMACS International Conference on Nonlinear Evolution Equations and Wave Phenomena. University of Georgia, Athens, Georgia, USA, April 02, 2015.Google Scholar
Lushnikov, P. M., Dyachenko, S. A. & Vladimirova, N. 2013 Beyond leading-order logarithmic scaling in the catastrophic self-focusing of a laser beam in Kerr media.. Phys. Rev. A 88, 013845.CrossRefGoogle Scholar
McLeod, J. B. 1987 The asymptotic behavior near the crest of waves of extreme form. Trans. Am. Math. Soc. 299, 299–302.CrossRefGoogle Scholar
McLeod, J. B. 1997 The Stokes and Krasovskii conjectures for the wave of greatest height. Stud. Appl. Maths 98, 311–333.CrossRefGoogle Scholar
Plotnikov, P. I. 1982 A proof of the Stokes conjecture in the theory of surface waves (in Russian). Dinamika Splosh. Sredy 57, 41–76; (English translation 2002 Stud. Appl. Math. 108, 217–244).Google Scholar
Plotnikov, P. I. 1991 Nonuniqueness of solutions of a problem on solitary waves and bifurcations of critical points of smooth functionals (in Russian). Izv. Akad. Nauk SSSR Ser. Mat. 55, 339–366; (English translation in 1992 Math. USSR-Izv. 38, 333357).Google Scholar
Plotnikov, P. I. & Toland, J. F. 2002 The Fourier coefficients of Stokes waves. In Nonlinear Problems in Mathematical Physics and Related Topics, I, International Mathematical Series, pp. 303–315. Kluwer/Plenum.CrossRefGoogle Scholar
Plotnikov, P. I. & Toland, J. F. 2004 Convexity of Stokes waves of extreme form. Arch. Rat. Mech. Anal. 171, 349–416.CrossRefGoogle Scholar
Schwartz, L. W. 1974 Computer extension and analytic continuation of Stokes’ expansion for gravity waves.. J. Fluid Mech. 62 (3), 553–578.CrossRefGoogle Scholar
Shargorodsky, E. & Toland, J. F. 2008 Bernoulli free-boundary problems. Mem. Amer. Math. Soc. 196, 349–416.Google Scholar
Stokes, G. G. 1847 On the theory of oscillatory waves. Trans. Camb. Phil. Soc. 8, 441–455.Google Scholar
Stokes, G. G. 1880a On the theory of oscillatory waves. Math. Phys. Papers 1, 197–229.Google Scholar
Stokes, G. G. 1880b Supplement to a paper on the theory of oscillatory waves. Math. Phys. Papers 1, 314–326.Google Scholar
Tanveer, S. 1991 Singularities in water waves and Rayleigh–Taylor instability. Proc. R. Soc. Lond. A 435, 137–158.Google Scholar
Tanveer, S.2013 Analytical approximation for 2-D nonlinear periodic deep water waves. arXiv:1309.5801.Google Scholar
Verner, J. H. 2010 Numerically optimal Runge–Kutta pairs with interpolants. Numer. Algorithms 53, 383–396.CrossRefGoogle Scholar
Wilkening, J. & Yu, J. 2012 Overdetermined shooting methods for computing standing water waves with spectral accuracy. Comput. Sci. Disc. 5, 014017.CrossRefGoogle Scholar
Williams, J. M. 1981 Limiting gravity waves in water of finite depth. Phil. Trans. R. Soc. Lond. A 302 (1466), 139–188.Google Scholar
Zakharov, V. E. & Dyachenkov, A. I. 1996 High-Jacobian approximation in the free surface dynamics of an ideal fluid.. Physica D 98, 652–664.Google Scholar
Zakharov, V. E., Dyachenko, A. I. & Vasiliev, O. A. 2002 New method for numerical simulation of nonstationary potential flow of incompressible fluid with a free surface. Eur. J. Mech. (B/Fluids) 21, 283–291.CrossRefGoogle Scholar