Article contents
Non-Boussinesq gravity currents propagating on different bottom slopes
Published online by Cambridge University Press: 13 February 2014
Abstract
Experiments on the non-Boussinesq gravity currents generated from an instantaneous buoyancy source propagating on an inclined boundary in the slope angle range 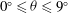 $0^{\circ } \le \theta \le 9^{\circ }$ with relative density difference in the range of
$0^{\circ } \le \theta \le 9^{\circ }$ with relative density difference in the range of 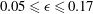 $0.05 \le \epsilon \le 0.17$ are reported, where
$0.05 \le \epsilon \le 0.17$ are reported, where 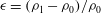 $\epsilon = (\rho _1-\rho _0)/\rho _0$, with
$\epsilon = (\rho _1-\rho _0)/\rho _0$, with 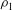 $\rho _1$ and
$\rho _1$ and 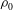 $\rho _0$ the densities of the heavy and light ambient fluids, respectively. We showed that a
$\rho _0$ the densities of the heavy and light ambient fluids, respectively. We showed that a 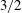 $3/2$ power-law,
$3/2$ power-law, 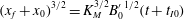 ${(x_f+x_0)}^{3/2}= K_M^{3/2} {B_0'}^{1/2} (t+t_{I0})$, exists between the front location measured from the virtual origin,
${(x_f+x_0)}^{3/2}= K_M^{3/2} {B_0'}^{1/2} (t+t_{I0})$, exists between the front location measured from the virtual origin, 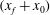 $(x_f+x_0)$, and time,
$(x_f+x_0)$, and time,  $t$, in the early deceleration phase for both the Boussinesq and non-Boussinesq cases, where
$t$, in the early deceleration phase for both the Boussinesq and non-Boussinesq cases, where 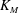 $K_M$ is a measured empirical constant,
$K_M$ is a measured empirical constant, 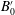 $B_0'$ is the total released buoyancy, and
$B_0'$ is the total released buoyancy, and 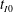 $t_{I0}$ is the
$t_{I0}$ is the  $t$-intercept. Our results show that
$t$-intercept. Our results show that 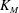 $K_M$ not only increases as the relative density difference increases but also assumes its maximum value at
$K_M$ not only increases as the relative density difference increases but also assumes its maximum value at 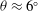 $\theta \approx 6^{\circ }$ for sufficiently large relative density differences. In the late deceleration phase, the front location data deviate from the
$\theta \approx 6^{\circ }$ for sufficiently large relative density differences. In the late deceleration phase, the front location data deviate from the 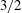 $3/2$ power-law and the flow patterns on
$3/2$ power-law and the flow patterns on 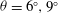 $\theta =6^{\circ },9^{\circ }$ slopes are qualitatively different from those on
$\theta =6^{\circ },9^{\circ }$ slopes are qualitatively different from those on 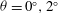 $\theta =0^{\circ },2^{\circ }$. In the late deceleration phase, we showed that viscous effects could become more important and another power-law,
$\theta =0^{\circ },2^{\circ }$. In the late deceleration phase, we showed that viscous effects could become more important and another power-law, 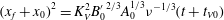 ${(x_f+x_0)}^{2}= K_{V}^{2} {B_0'}^{2/3} {{A}^{1/3}_0} {\nu }^{-1/3} (t+t_{V0})$, applies for both the Boussinesq and non-Boussinesq cases, where
${(x_f+x_0)}^{2}= K_{V}^{2} {B_0'}^{2/3} {{A}^{1/3}_0} {\nu }^{-1/3} (t+t_{V0})$, applies for both the Boussinesq and non-Boussinesq cases, where 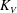 $K_V$ is an empirical constant,
$K_V$ is an empirical constant, 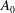 $A_0$ is the initial volume of heavy fluid per unit width,
$A_0$ is the initial volume of heavy fluid per unit width,  $\nu $ is the kinematic viscosity of the fluids, and
$\nu $ is the kinematic viscosity of the fluids, and 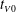 $t_{V0}$ is the
$t_{V0}$ is the  $t$-intercept. Our results also show that
$t$-intercept. Our results also show that 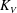 $K_V$ increases as the relative density difference increases and
$K_V$ increases as the relative density difference increases and 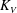 $K_V$ assumes its maximum value at
$K_V$ assumes its maximum value at 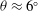 $\theta \approx 6^{\circ }$.
$\theta \approx 6^{\circ }$.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 39
- Cited by




