Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-05-06T23:02:49.876Z Has data issue: false hasContentIssue false
  • English
  • Français

SYLVESTER–GALLAI TYPE THEOREMS FOR APPROXIMATE COLLINEARITY

Part of: Discrete geometry Theory of error-correcting codes and error-detecting codes

Published online by Cambridge University Press:  28 March 2014

ALBERT AI ,
ZEEV DVIR ,
SHUBHANGI SARAF  and
AVI WIGDERSON
ALBERT AI
Affiliation:
Department of Mathematics, University of California, Berkeley, USA
ZEEV DVIR
Affiliation:
Department of Computer Science and Department of Mathematics, Princeton University, USAzdvir@princeton.edu, zeev.dvir@gmail.com
SHUBHANGI SARAF
Affiliation:
Department of Computer Science and Department of Mathematics, Rutgers University, USA
AVI WIGDERSON
Affiliation:
School of Mathematics, Institute for Advanced Study, USA

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study questions in incidence geometry where the precise position of points is ‘blurry’ (for example due to noise, inaccuracy or error). Thus lines are replaced by narrow tubes, and more generally affine subspaces are replaced by their small neighborhood. We show that the presence of a sufficiently large number of approximately collinear triples in a set of points in 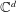${\mathbb{C}}^d$ implies that the points are close to a low dimensional affine subspace. This can be viewed as a stable variant of the Sylvester–Gallai theorem and its extensions. Building on the recently found connection between Sylvester–Gallai type theorems and complex locally correctable codes (LCCs), we define the new notion of stable LCCs, in which the (local) correction procedure can also handle small perturbations in the Euclidean metric. We prove that such stable codes with constant query complexity do not exist. No impossibility results were known in any such local setting for more than two queries.

MSC classification

Secondary: 52C35: Arrangements of points, flats, hyperplanes 94B65: Bounds on codes
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 2 , 01 July 2014 , e3
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© The Author(s) 2014

References

Alon, N., ‘Perturbed identity matrices have high rank: Proof and applications’, Combin. Probab. Comput. 18 (1-2) (2009), 3–15.CrossRefGoogle Scholar
Barak, B., Dvir, Z., Wigderson, A. and Yehudayoff, A., ‘Rank bounds for design matrices with applications to combinatorial geometry and locally correctable codes’, Proceedings of the 43rd annual ACM symposium on Theory of computing, STOC ’11 (ACM, 2011) 519–528.CrossRefGoogle Scholar
Bhattacharyya, A., Dvir, Z., Shpilka, A. and Saraf, S., ‘Tight lower bounds for 2-query lccs over finite fields’, Proc. of FOCS 2011, 2011, 638–647.CrossRefGoogle Scholar
Borwein, P. and Moser, O. J., ‘A survey of Sylvester’s problem and its generalizations’, Aequationes Math. 40 (1990).CrossRefGoogle Scholar
Candes, E. and Tao, T., ‘Decoding by linear programming’, IEEE Trans. Inform. Theory 51 (2005), 4203–4215.CrossRefGoogle Scholar
Donoho, D., ‘Compressed sensing’, IEEE Trans. Inf. Theory 52 (2006), 1289–1306.CrossRefGoogle Scholar
Dvir, Z., ‘Incidence theorems and their applications’, Found. Trends Theor. Comput. Sci. 6 (2012), 257–393.CrossRefGoogle Scholar
Dvir, Z., Saraf, S. and Wigderson, A., ‘Improved rank bounds for design matrices and a new proof of Kelly’s theorem’, Forum of Math. Sigma (2013), (to appear).Google Scholar
Dvir, Z., ‘On matrix rigidity and locally self-correctable codes’, Comput. Complexity 20 (2011), 367–388.CrossRefGoogle Scholar
Dwork, C., McSherry, F. and Talwar, K., ‘The price of privacy and the limits of LP decoding’, Proceedings of the thirty-ninth annual ACM symposium on theory of computing, STOC ’07 (ACM, 2007), 85–94.CrossRefGoogle Scholar
Guruswami, V., Lee, J. R. and Wigderson, A., ‘Expander codes over reals, euclidean sections, and compressed sensing’, Proceedings of the 47th annual Allerton conference on Communication, control, and computing, Allerton’09 (Piscataway, NJ, USA, IEEE Press, 2009) 1231–1234.CrossRefGoogle Scholar
Hoffman, A. J. and Wielandt, H. W., ‘The variation of the spectrum of a normal matrix’, Duke Math. J. 20 (1953), 37–39.CrossRefGoogle Scholar
Kashin, B. S. and Temlyakov, V. N., ‘A remark on compressed sensing’, 2007. Available at: http://www.dsp.ece.rice.edu/cs/KT2007.pdf.Google Scholar
Katz, J. and Trevisan, L., ‘On the efficiency of local decoding procedures for error-correcting codes’, 32nd ACM Symposium on Theory of Computing (STOC), 2000, 80–86.CrossRefGoogle Scholar
Kelly, L. M., ‘A resolution of the Sylvester–Gallai problem of J. P. Serre’, Discrete Comput. Geom. 1 (1986), 101–104.CrossRefGoogle Scholar
Kerenidis, I. and de Wolf, R., ‘Exponential lower bound for 2-query locally decodable codes via a quantum argument’, J. Comput. System Sci. 69 (2004), 395–420.CrossRefGoogle Scholar
Rudelson, M. and Vershynin, R., ‘Geometric approach to error correcting codes and reconstruction of signals’, Int. Math. Res. Not. 64 (2005), 4019–4041.CrossRefGoogle Scholar
Tao, T., ‘From rotating needles to stability of waves: emerging connections between combinatorics, analysis, and PDE’, Not. Am. Math. Soc. 48 (2001), 294–303.Google Scholar
Woodruff, D., ‘New lower bounds for general locally decodable codes’, Electronic Colloquium on Computational Complexity (ECCC), TR07-006, 2007.Google Scholar
Yekhanin, S., ‘Locally decodable codes’, Foundations and trends in theoretical computer science, 2011, to appear. (Preliminary version available for download at http://research.microsoft.com/en-us/um/people/yekhanin/Papers/LDC_now.pdf).CrossRefGoogle Scholar