Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-25T12:20:40.121Z Has data issue: false hasContentIssue false
  • English
  • Français

Improved Ramsey-type results for comparability graphs

Part of: Graph theory Ordered sets

Published online by Cambridge University Press:  13 August 2020

Dániel Korándi  and
István Tomon
Dániel Korándi*
Affiliation:
Institute of Mathematics, EPFL, 1015 Lausanne, Switzerland
István Tomon
Affiliation:
Institute of Mathematics, EPFL, 1015 Lausanne, Switzerland
*
*Corresponding author. Email: daniel.korandi@epfl.ch
Get access Rights & Permissions [Opens in a new window]

Abstract

Several discrete geometry problems are equivalent to estimating the size of the largest homogeneous sets in graphs that happen to be the union of few comparability graphs. An important observation for such results is that if G is an n-vertex graph that is the union of r comparability (or more generally, perfect) graphs, then either G or its complement contains a clique of size 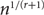$n^{1/(r+1)}$ .

This bound is known to be tight for 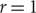$r=1$ . The question whether it is optimal for 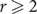$r\ge 2$ was studied by Dumitrescu and Tóth. We prove that it is essentially best possible for 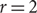$r=2$ , as well: we introduce a probabilistic construction of two comparability graphs on n vertices, whose union contains no clique or independent set of size 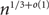$n^{1/3+o(1)}$ .

Using similar ideas, we can also construct a graph G that is the union of r comparability graphs, and neither G nor its complement contain a complete bipartite graph with parts of size 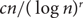$cn/{(log n)^r}$ . With this, we improve a result of Fox and Pach.

MSC classification

Primary: 05C35: Extremal problems
Secondary: 06A07: Combinatorics of partially ordered sets 05C55: Generalized Ramsey theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 29 , Issue 5 , September 2020 , pp. 747 - 756
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported in part by SNSF grants 200020-162884 and 200021-175977.

References

Ajtai, M., Komlós, J. and Szemerédi, E. (1980) A note on Ramsey numbers. J. Combin. Theory Ser. A 29 354–360.CrossRefGoogle Scholar
Bollobás, B. (1988) The isoperimetric number of random regular graphs. European J. Combin. 9 241–244.CrossRefGoogle Scholar
Chen, X., Pach, J., Szegedy, M. and Tardos, G. (2009) Delaunay graphs of point sets in the plane with respect to axis-parallel rectangles. Random Struct. Algorithms 34 11–23.CrossRefGoogle Scholar
Dumitrescu, A. and Tóth, G. (2002) Ramsey-type results for unions of comparability graphs. Graphs Combin. 18 245–251.CrossRefGoogle Scholar
Fox, J. (2006) A bipartite analogue of Dilworth’s theorem. Order 23 197–209.CrossRefGoogle Scholar
Fox, J. and Pach, J. (2009) A bipartite analogue of Dilworth’s theorem for multiple partial orders. European J. Combin. 30 1846–1853.CrossRefGoogle Scholar
Fox, J., Pach, J. and Tóth, C. D. (2010) Turán-type results for partial orders and intersection graphs of convex sets. Israel J. Math. 178 29–50.CrossRefGoogle Scholar
Har-Peled, S. and Smorodinsky, S. (2005) Conflict-free coloring of points and simple regions in the plane. Discrete Comput. Geom. 34 47–70.CrossRefGoogle Scholar
Kostochka, A. (2004) Coloring intersection graphs of geometric figures with a given clique number. In Towards a Theory of Geometric Graphs, Vol. 342 of Contemporary Mathematics, pp. 127–138, AMS.Google Scholar
Kynčl, J. (2012) Ramsey-type constructions for arrangements of segments. European J. Combin. 33 336–339.CrossRefGoogle Scholar
Larman, D., Matoušek, J., Pach, J. and Törőcsik, J. (1994) A Ramsey-type result for convex sets. Bull. Lond. Math. Soc. 26 132–136.CrossRefGoogle Scholar
McGuinness, S. (2000) Colouring arcwise connected sets in the plane I. Graphs Combin. 16 429–439.CrossRefGoogle Scholar
Morgenstern, M. (1994) Existence and explicit constructions of q+1 regular Ramanujan graphs for every prime power q. J. Combin. Theory Ser. B 62 44–62.CrossRefGoogle Scholar
Pach, J. and Tomon, I. (2020) On the chromatic number of disjointness graphs of curves. J. Combin. Theory Ser. B 144 167–190.CrossRefGoogle Scholar
Pach, J. and Törőcsik, J. (1994) Some geometric applications of Dilworth’s theorem. Discrete Comput. Geom. 12 1–7.CrossRefGoogle Scholar
Perepelitsa, I. G. (2003) Bounds on the chromatic number of intersection graphs of sets in the plane. Discrete Math. 262 221–227.CrossRefGoogle Scholar
Raab, M. and Steger, A. (1998) ‘Balls into bins’: a simple and tight analysis. In Randomization and Approximation Techniques in Computer Science, Vol. 1518 of Lecture Notes in Computer Science, pp. 159–170, Springer.Google Scholar
Szabó, T. personal communication.Google Scholar
Tomon, I. (2016) Turán-type results for complete h-partite graphs in comparability and incomparability graphs. Order 33 537–556.CrossRefGoogle Scholar