Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-18T05:29:37.094Z Has data issue: false hasContentIssue false
  • English
  • Français

On the essential spectrum of phase-space anisotropic pseudodifferential operators

Published online by Cambridge University Press:  02 July 2012

MARIUS MĂNTOIU
MARIUS MĂNTOIU*
Affiliation:
Departamento de Matemáticas, Facultad de Ciencias, Universidad de Chile, Las Palmeras 3425, Casilla 653, Santiago, Chile e-mail: mantoiu@uchile.cl
Get access Rights & Permissions [Opens in a new window]

Abstract

A phase-space anisotropic operator in 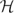=L2(ℝn) is a self-adjoint operator whose resolvent family belongs to a natural C*-completion of the space of Hörmander symbols of order zero. Equivalently, each member of the resolvent family is norm-continuous under conjugation with the Schrödinger unitary representation of the Heisenberg group. The essential spectrum of such a phase-space anisotropic operator is the closure of the union of usual spectra of all its “phase-space asymptotic localizations”, obtained as limits over diverging ultrafilters of ℝn×ℝn-translations of the operator. The result extends previous analysis of the purely configurational anisotropic operators, for which only the behavior at infinity in ℝn was allowed to be non-trivial.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 154 , Issue 1 , January 2013 , pp. 29 - 39
Copyright
Copyright © Cambridge Philosophical Society 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Amrein, W. O., Boutet de Monvel, A. and Georgescu, V.C 0-Groups, Commutator Methods and Spectral Theory of N-Body Hamiltonians (Birkhäuser, Basel, 1996).Google Scholar
[2]Beltiţă, I. and Măntoiu, M. Rieffel quantization and twisted crossed products. submitted.Google Scholar
[3]Bourbaki, N.Eléments de Mathématique: Topologie générale (Hermann, Paris, 1971). Ch. 14Google Scholar
[4]Davies, E. B.Heat Kernels and Spectral Theory (Cambridge University Press, 1989).CrossRefGoogle Scholar
[5]Davies, E. B.Decomposing the essential spectrum. J. Funct. Anal. 257 no. 2, (2009), 506–536.CrossRefGoogle Scholar
[6]Davies, E. B. and Georgescu, V.C*-algebras associated with some second order differential operators. Preprint ArXiV and to appear in J. Operator Theory.Google Scholar
[7]Folland, G. B.Harmonic Analysis in Phase Space. Ann. Math. Stud. 122 (Princeton University Press, Princeton, NJ, 1989).CrossRefGoogle Scholar
[8]Georgescu, V.On the structure of the essential spectrum of elliptic operators in metric spaces. J. Funct. Anal. 260 (2011), 1734–1765.CrossRefGoogle Scholar
[9]Georgescu, V. and Iftimovici, A.Crossed Products of C*-algebras and spectral analysis of quantum Hamiltonians. Commun. Math. Phys. 228 (2002), 519–560.CrossRefGoogle Scholar
[10]Georgescu, V. and Iftimovici, A.Riesz Kolmogorov compactness criterion, Lorentz convergence and Ruelle theorem on locally compact Abelian groups. Potential Analysis 20, (2004) 265–284.CrossRefGoogle Scholar
[11]Georgescu, V. and Iftimovici, A.Localizations at infinity and essential spectrum of quantum Hamiltonians. I. General Theory. Rev. Math. Phys. 18 (4), (2006), 417–483.CrossRefGoogle Scholar
[12]Helffer, B. and Mohamed, A.Caractérisation du spectre essentiel de l'opérateur de Schrödinger avec un champ magnétique. Ann. Inst. Fourier 38 no. 2 (1988), 95–112.CrossRefGoogle Scholar
[13]Kasprzak, P.Rieffel deformation via crossed products. J. Funct. Anal. 257 no. 5 (2009), 1228–1332.CrossRefGoogle Scholar
[14]Last, Y. and Simon, B.The essential spectrum of Schrödinger, Jacobi and CMV operators. J. d'Analyse Math. 98 (2006), 183–220.CrossRefGoogle Scholar
[15]Lauter, R. and Nistor, V.Analysis of geometric operators on open manifolds: a Groupoid Approach. In Quantization of Singular Symplectic Quotient. Progr. Math. 198 (Birkhäuser, Basel 2001), 181–229.CrossRefGoogle Scholar
[16]Măntoiu, M.Compactifications, dynamical systems at infinity and the essential spectrum of generalized Schödinger operators. J. Reine Angew. Math. 550 (2002), 211–229.Google Scholar
[17]Măntoiu, M. Rieffel's pseudodifferential calculus and spectral analysis for quantum Hamiltonians. Preprint ArXiV and to appear in Ann. Inst. Fourier.Google Scholar
[18]Măntoiu, M., Purice, R. and Richard, S.Spectral and propagation results for magnetic Schrödinger operators; a C*-algebraic framework. J. Funct. Anal. 250 (2007), 42–67.CrossRefGoogle Scholar
[19]Rieffel, M. A.Deformation quantization for actions of ℝd. Memoirs Amer. Math. Soc. 506 (1993).Google Scholar
[20]Rabinovich, V. S., Roch, S. and Roe, J.Fredholm indices of band-dominated operators. Int. Eq. Op. Th. 49 (2004), 221–238.Google Scholar
[21]Rabinovich, V. S., Roch, S. and Silbermann, B.Limit Operators and their Applications In Operator Theory. Operator Theory: Adv. and Applic. 150 (Birkhäuser, Basel, 2004).Google Scholar
[22]Raeburn, I. and Williams, D.Morita Equivalence and Continuous-Trace C*-Algebras. Math. Surv. Monogr. 60 (American Mathematical Society, 1998).CrossRefGoogle Scholar
[23]Röckner, M. and Wielens, N.Dirichlet Forms - Closability and Change of Speed Measure. In Infinite Dimensional Analysis and Stochastic Processes, Rese. Notes in Mathe. 124 (Pitman 1985), 119–144.Google Scholar
[24]Woronowicz, S. L.Unbounded elements affiliated with C*-algebras and non-compact quantum groups. Commun. Math. Phys. 136 (1991), 399–432.CrossRefGoogle Scholar