Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-24T03:16:33.637Z Has data issue: false hasContentIssue false
  • English
  • Français

A SUFFICIENT CONDITION FOR A GRAPH TO BE A FRACTIONAL (f, n)-CRITICAL GRAPH

Published online by Cambridge University Press:  29 March 2010

SIZHONG ZHOU
SIZHONG ZHOU*
Affiliation:
School of Mathematics and Physics, Jiangsu University of Science and Technology, Mengxi Road 2, Zhenjiang, Jiangsu 212003, People's Republic of China e-mail: zsz_cumt@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let a, b and n be non-negative integers such that 1 ≤ a ≤ b, and let G be a graph of order p with 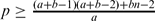and f be an integer-valued function defined on V(G) such that a ≤ f(x) ≤ b for all x ∈ V(G). Let h: E(G) → [0, 1] be a function. If ∑e∋xh(e) = f(x) holds for any x ∈ V(G), then we call G[Fh] a fractional f-factor of G with indicator function h, where Fh = {e ∈ E(G): h(e) > 0}. A graph G is called a fractional (f, n)-critical graph if after deleting any n vertices of G the remaining graph of G has a fractional f-factor. In this paper, it is proved that G is a fractional (f, n)-critical graph if 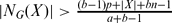for every non-empty independent subset X of V(G), and 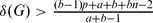. Furthermore, it is shown that the result in this paper is best possible in some sense.

Keywords

05C70
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 52 , Issue 2 , May 2010 , pp. 409 - 415
Copyright
Copyright © Glasgow Mathematical Journal Trust 2010

References

REFERENCES

1.Bondy, J. A. and Murty, U. S. R., Graph theory with applications (Macmillan, London, 1976).CrossRefGoogle Scholar
2.Cai, J., Liu, G. and Hou, J., The stability number and connected [k, k+1]-factor in graphs, Appl. Math. Lett. 22 (6) (2009), 927–931.CrossRefGoogle Scholar
3.Liu, H. and Liu, G., Binding number and minimum degree for the existence of (g, f, n)-critical graphs, J. Appl. Math. Comput. 29 (1–2) (2009), 207–216.CrossRefGoogle Scholar
4.Liu, G. and Zhang, L., Toughness and the existence of fractional k-factors of graphs, Discrete Math. 308 (2008), 1741–1748.CrossRefGoogle Scholar
5.Matsuda, H., Fan-type results for the existence of [a, b]-factors, Discrete Math. 306 (2006), 688–693.Google Scholar
6.Shirerman, E. R. and Ullman, D. H., Fractional graph theory (John Wiley, New York, 1997).Google Scholar
7.Yu, J., Liu, G., Ma, M. and Cao, B., A degree condition for graphs to have fractional factors, Adv. Math. 35 (5) (2006), 621–628.Google Scholar
8.Zhou, S., Independence number, connectivity and (a, b, k)-critical graphs, Discrete Math. 309 (12) (2009), 4144–4148.CrossRefGoogle Scholar
9.Zhou, S., A sufficient condition for a graph to be an (a, b, k)-critical graph, Int. J. Comput. Math.Google Scholar
10.Zhou, S., Some results on fractional k-factors, Indian J. Pure Appl. Math. 40 (2) (2009), 113–121.Google Scholar
11.Zhou, S., Toughness and the existence of fractional k-factors, Math. Prac. Theory 36 (6) (2006), 255–260 (in Chinese).Google Scholar
12.Zhou, S. and Jiang, J., Notes on the binding numbers for (a, b, k)-critical graphs, Bull. Aust. Math. Soc. 76 (2) (2007), 307–314.Google Scholar
13.Zhou, S. and Shen, Q., On fractional (f, n)-critical graphs, Inf. Process. Lett. 109 (14) (2009), 811–815.CrossRefGoogle Scholar