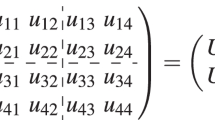1 Introduction

Quantum incompatibility is a fundamental property in quantum physics, which is quite different from classical physics [1]. In quantum physics, some observables or measurements cannot commute with each other, which implies that we cannot acquire precise information from them simultaneously. Quantum incompatibility is considered as an important resource for quantum phenomena and information processing, including quantum nonlocality [2], measurement uncertainty relations [3, 4], uncertain relation [4], contextuality [5, 6], and quantum steering [7–9]. Therefore, it is important to witness and quantify quantum incompatibility as a resource for developing quantum applications.

In order to detect incompatibility, some methods based on entanglement schemes have been proposed [3, 10–12]. In these entanglement-based schemes, spacelike separated entanglement sources are required. Fortunately, entanglement is confirmed not necessarily needed for quantum incompatibility features, which provides an alternative for detecting quantum incompatibility. Recently, quantum state discrimination (QSD) tasks, applied in detecting quantum coherence [13, 14], entropic uncertainty relations, accessible information [14, 15], have been applied in witnessing quantum incompatibility [8, 13, 14, 16–22].

In order to investigate incompatibility witnesses quantificationally, it is convenient to prepare two disjoint state ensembles as two sets of mutually unbiased bases (MUBs) under different noise levels. MUB measurements are among of the most representative incompatible measurements and have been applied in many quantum information protocols [23–26].

Recently, incompatibility witnesses based on hyperplanes have been established [16], linear incompatibility witnesses (LIWs) have been verified [18] and the robustness of incompatibility has been proposed [8]. However, the geometrical properties of the witnesses need to be discussed and the robustness of incompatibility is difficult to calculate. For example, it is difficult to find the optimal ensembles for practical QSD scenarios and contrast the incompatibility of two pairs of positive operator valued measurements (POVMs), which indicates a need for a framework to describe quantum incompatibility processes.

In this paper, we construct a geometrical framework for quantum incompatibility processes. Firstly, we discuss the incompatibility witness based on the gap of prior- and post-measurement guessing probabilities in a two-part QSD scenario of noisy MUBs. Secondly, we discuss the unified and geometrical explanations for the witness and define a new quantifier associated with geometrical properties to quantify incompatibility. Furthermore, we explore the incompatibility of POVMs only using the information of given POVMs in the first application and the incompatibility of POVMs which can be discriminated by MUB. Finally, we show advantages of the framework in describing incompatibility and associate the quantifier with quantum resources.

2 Nonlinear witnesses based on quantum state discrimination tasks

In this section, we pave the way to a geometrical framework for incompatibility. Firstly, we introduce quantum state discrimination tasks, which are the basic physical process for the incompatibility witness. Secondly, we discuss the incompatibility witnessed based on noisy MUBs, where the geometrical properties of the witnesses appear, and discuss the witnesses varying with dimensions and three cases for detecting incompatibility.

2.1 Quantum state discrimination

Consider a pair of POVMs M and N labeled {Mx}x and {Ny}y, satisfying \(\Sigma _{x}M_{x}=\mathbb {I} \) and \(\Sigma _{y}N_{y}=\mathbb {I}\) with outcomes x and y, respectively. M and N are compatible if there exists a joint or parent measurement J labeled Jx,y satisfying ΣyJx,y=Mx and ΣxJx,y=Ny.

In a two-party QSD scenario, Alice prepares two ensembles of quantum states \(\mathcal {E}_{X}=\{ p(x),\Psi _{x}\}_{x} \) and \(\mathcal {E}_{Y}=\{ p(y),\Phi _{y}\}_{y}\), where p(x) and p(y) are the probability distributions of states Ψx and Φy, respectively. Then Bob receives a merged ensemble \(\mathcal {E}\) with a proportion parameter q as follows:

$$ \mathcal{E} = q\mathcal{E}_{X}+(1-q)\mathcal{E}_{Y}=\{ q p(x),\Psi_{x};(1-q)p(y),\Phi_{y} \}_{x,y}, $$
(1)

where q∈(0,1].

Bob has two strategies to guess the label of the state sent from Alice. If the information of given ensemble \(\mathcal {E}_{X}\) or \(\mathcal {E}_{Y}\) is announced before the measurement, the guesser Bob will perform corresponding measurement M or N to detect the state from ensembles \(\mathcal {E}_{X}\) or \(\mathcal {E}_{Y}\), respectively. The probability of guessing the correct label for one ensemble is \( P_{\text {guess}}(\mathcal {E}_{X};M)=\sum _{x} p(x) \text {Tr}(M_{x} \Psi _{x})\). Then the total guessing probability with prior information can be written out as follows:

$$ P_{\text{guess}}^{\text{prior}}(\mathcal{E} ; M, N)=q P_{\text{guess}}\!\left(\mathcal{E}_{X} ; M\right)+(1\!-q) P_{\text{guess}}\left(\mathcal{E}_{Y} ; N\right). $$
(2)

In contrast, if the information of the given set \(\mathcal {E}_{X}\) or \(\mathcal {E}_{Y}\) is announced after the measurement, Bob has to use a fixed measurement J labeled with a cartesian product (X,Y), which is the outcome of measuring two ensembles simultaneously, and adjust J after each round to match the optimal joint measurement. Then the post information guessing probability can be written out as follows:

$$ P_{\text{guess}}^{\text{post}}(\mathcal{E})=\max_{J} P_{\text{guess}}(\mathcal{E} ; J). $$
(3)

If POVMs M and N are compatible, their observation (X,Y) will be divided into compatible pairs \(\mathcal {O}_{X,Y}^{\text {com}} \), else into the incompatible pairs \(\mathcal {O}_{X,Y}^{\text {inc}} \equiv \overline {\mathcal {O}_{X, Y}^{\text {com}}} \). It has been proven that for incompatible measurements, there always exists a partitioned state ensemble \(\mathcal {E}\) such that \( P_{\text {guess}}^{\text {post}}\left (\mathcal {E}\right)<P_{\text {guess}}^{\text {prior}}\left (\mathcal {E}; M, N\right)\). Hence the incompatibility witnesses separating \(\mathcal {O}_{X,Y}^{\text {com}} \) and \(\mathcal {O}_{X,Y}^{\text {inc}} \) in the form of hyperplanes can be written as follows [16]:

$$ W=P_{\text{guess}}^{\text{post}}\left(\mathcal{E}\right)-P_{\text{guess}}^{\text{prior}}\left(\mathcal{E}; M, N\right). $$
(4)

2.2 Incompatibility witnesses based on noisy MUBs

Here, we explore the incompatibility of d-dimension noisy MUB measurements (M,N) with corresponding ensembles \((\mathcal {E}_{X},\mathcal {E}_{Y})\) with noises:

$$ \begin{aligned} &M:\left\{s_{x}\left\vert \psi_{i}^{A}\right\rangle\left\langle\psi_{i}^{A}\right\vert +\left(1-s_{x}\right) \mathbb{I} / d\right\}_{i}, \\ &N:\left\{s_{y}\left\vert \phi_{j}^{B}\right\rangle\left\langle\phi_{j}^{B}\right\vert +\left(1-s_{y}\right) \mathbb{I} / d\right\}_{j}, \end{aligned} $$
(5)

where i,j∈(1,2,⋯,d) and sx,sy∈(0,1].

Parameters sx and sy represent the sharpness of MUB measurements, and the corresponding ensembles under noise levels labeled (rx,ry) are:

$$ \begin{aligned} &\mathcal{E}_{X}:\left\{\frac{1}{d}, r_{x}\left\vert \psi_{i}^{A}\right\rangle\left\langle\psi_{i}^{A}\right\vert +\left(1-r_{x}\right) \mathbb{I} / d\right\}_{i}, \\ &\mathcal{E}_{Y}:\left\{\frac{1}{d}, r_{y}\left\vert \phi_{j}^{B}\right\rangle\left\langle\phi_{j}^{B}\right\vert +\left(1-r_{y}\right) \mathbb{I} / d\right\}_{j}, \end{aligned} $$
(6)

where i,j∈(1,2,⋯,d) and rx,ry∈(0,1].

In this QSD task, we set a balanced proportion parameter \(q = \frac {1}{2} \) and the probability for every state in the ensembles is \(\frac {1}{d}\). The optimal joint measurement J(A,B) for a pair of MUBs is given in Ref. [27]:

$$ \begin{aligned} J_{i, j}=& b(r_{x}\vert \psi_{i}\rangle\langle\psi_{i}\vert +r_{y}\vert \phi_{j}\rangle\langle\phi_{j}\vert)-\frac{d c}{d-1}(\vert \psi_{i}\rangle\langle\psi_{i}\vert\\&+\vert \phi_{j}\rangle\langle\phi_{j}\vert -\vert \psi_{i}\rangle\langle\psi_{i}\vert \vert \phi_{j}\rangle \langle\phi_{j}\vert -\vert \phi_{j}\rangle \langle\phi_{j}\vert \vert \psi_{i}\rangle\langle\psi_{i}\vert), \end{aligned} $$
(7)

where

$$\begin{aligned} b=\frac{1}{\sqrt{r_{x}^{2}+r_{y}^{2}-\frac{2d-4}{d} r_{x} r_{y}}},c=\frac{1}{2}\left(\frac{r_{x}+r_{y}}{\sqrt{r_{x}^{2}+r_{y}^{2}-\frac{2d-4}{d} r_{x} r_{y}}}-1\right). \end{aligned} $$

Here, we can give the mathematical forms of \(P_{\text {guess}}^{\text {post}}\) and \(P_{\text {guess}}^{\text {prior}}\), which are detailed in Appendix A:

$$ \begin{aligned} P_{\text{guess}}^{\text{post}}&=\frac{1}{4} \sqrt{r_{x}^{2}+r_{y}^{2}-\frac{2d-4}{d} r_{x} r_{y}}+\frac{d-2}{4d}(r_{x}+r_{y})+\frac{1}{d},\\ P_{\text{guess}}^{\text{prior}}&=\frac{d-1}{2d}\left(r_{x} s_{x}+r_{y} s_{y}\right)+\frac{1}{d}. \end{aligned} $$
(8)

Recalling Eq. (4), we can write out the incompatibility witness W, which represents the boundary between compatibility and incompatibility:

$$ \begin{aligned} W=&\frac{1}{4} \sqrt{r_{x}^{2}+r_{y}^{2}-\frac{2d-4}{d} r_{x} r_{y}}+\frac{d-2}{4d}(r_{x}+r_{y})\\&-\frac{d-1}{2d}\left(r_{x} s_{x}+r_{y} s_{y}\right). \end{aligned} $$
(9)

In a mathematical perspective, this function is a nonlinear witness of four parameters (rx,ry,sx,sy). When parameters (rx,ry) are fixed, the function will become a linear function for (sx,sy), which is the form of linear witnesses corresponding to the hyperplanes separating \(\mathcal {O}_{X,Y}^{\text {com}}\) and \(\mathcal {O}_{X,Y}^{\text {inc}}\) [18].

Note that the special case that W=0 implies the boundary curve between compatibility and incompatibility in Fig. 1. According to Eq. (9), we can write out the coordinate of the boundary curve in Eq. (10), which we discuss detailly in the next section for the construction of the geometrical framework.

Fig. 1
figure 1

The witnesses for several dimensions have been shown as convex curves and the cases for the incompatibility witness are discussed. a The cases d=2,3,4,6,100 and ∞. The curves of the boundary for W=0 are ellipses. The case d=2 and d=∞ are special, which are a quadrant and line, respectively. The red point shows compatible POVMs in the case d=6, but incompatible POVMs in the case d=100. b There are cases for the incompatibility witness. In the case d=5, the yellow point and red line are tangent point and its tangent line. There are three cases in incompatibility witnesses: olive point: inside the curve; purple: outside the curve but inside the line; orange point: outside the line

Full size image

We discuss the properties of the boundary curve varying with dimensions in Fig. 1a. Intuitively, when the dimension increases, the incompatibility between two MUBs also increases [28]. The red point implies the same noise levels of MUB measurements show compatible or incompatible due to dimensions.

There are three possible cases in practical QSD scenario in Fig. 1b.

  1. 1.

    W<0: Incompatibility is detected existent for this four parameters (rx,ry,sx,sy), which corresponds to the orange point in Fig. 1b.

  2. 2.

    W=0: \(P_{\text {guess}}^{\text {post}}=P_{\text {guess}}^{\text {prior}}\), which is the boundary between compatibility and incompatibility.

  3. 3.

    W>0: Compatibility is detected existent even though the joint measurement performed is not optimal, which corresponds to the olive and purple points in Fig. 1b.

In conclusion, we have discussed the properties of the nonlinear incompatibility witness (NLIW) with four parameters (rx,ry,sx,sy). The boundary between compatibility and incompatibility for a pair of noisy MUB ensembles labeled with (rx,ry) can be represented as a two-dimension convex curve, which implies geometrical properties in the model originated from incompatibility witnesses. Here, we name the model for convex model because the model is essentially originated from the convex combination of partitioned information. In the following contents, we will inspect the model and construct a more intuitive framework for its geometrical properties.

3 The geometrical framework for quantum incompatibility

In this section, we start to construct a framework for incompatibility. Firstly, we give unified and geometrical explanations for incompatibility witnesses in order to discuss the properties in a framework. Secondly, we construct a quantifier of incompatibility based on these explanations, which is associated with the geometrical properties in the framework. Thirdly, we discuss two applications to show the applicability of this framework. Finally, we confirmed that the new-defined quantifier can characterize the resource of incompatibility.

3.1 Unified and geometrical explanations for the witness

In practical QSD scenario, the function of NLIW has four parameters (rx,ry,sx,sy), where four parameters (rx,ry,sx,sy) can be adjusted independently.

It is necessary for the four parameters to have a unified explanation. Recalling Eq. (5), the MUB part in measurements represents the incompatibility part and the white noise represents the compatibility part of POVMs. Recalling Eq. (6), the MUB part in ensembles represents distinguishing POVMs, which leads to the gap of guessing probability of different strategies, and the white noise represents no operation with outcomes of average probability distributions. In one word, (sx,sy) labels POVMs and (rx,ry) scales the incompatibility.

It is worth noting that the operators in Eq. (5) are positive if and only if \(s_{x},s_{y}\in \left [\frac {1}{1-d},1\right ] \) [16], while in the practical incompatibility framework, we restrict them to positive values sx,sy∈(0,1] as noisy versions of the sharp measurements [29].

Then we start to discuss the geometrical explanation for the four parameters. In Fig. 1b, an arbitrary fixed (rx,ry) corresponds to a fixed hyperplane, and all (rx,ry) is supposed to draw corresponding hyperplanes which together form the convex curve. Therefore, we can write out the coordinate of the point on the boundary curve, which is detailed in Appendix B:

$$ \begin{aligned} s_{x}&=\frac{1}{2(d-1)}\left[ \frac{dk-(d-2)}{\sqrt{k^{2}+1-\frac{2d-4}{d} k}}+(d-2)\right], \\ s_{y}&=\frac{1}{2(d-1)}\left[ \frac{d-(d-2)k}{\sqrt{k^{2}+1-\frac{2d-4}{d} k}}+(d-2)\right], \end{aligned} $$
(10)

where \(k= \frac {r_{x}}{r_{y}}\).

The curve as a boundary on (sx,sy) is a function of k and not directly relevant to the value of (rx,ry). Obviously, a set of (sx,sy) can be described by a point in the cartesian coordinate system, while a set of (rx,ry) corresponds to a k. A fixed k in Eq. (10) can be seen as a point \((s_{x_{0}},s_{y_{0}})\) on the curve. The transformation from k to \((s_{x_{0}},s_{y_{0}})\) implies the optimal joint measurement can be replaced by two equivalent measurements \((s_{x_{0}},s_{y_{0}})\) geometrically.

Then the post-measurement guessing probability can be replaced by a point on the convex curve as \( P^{Post} =P(s_{x_{0}},s_{y_{0}})\) with \((s_{x_{0}},s_{y_{0}})\) satisfying Eq. (10). What’s more, the prior-measurement guessing probability of partitioned measurements can replaced by a point (sx,sy) as PPrior=P(sx,sy). As a result, the four parameters are unified as points in the geometrical convex model.

3.2 Quantifying the degree of incompatibility

The degree of incompatibility has been characterized by the robustness of incompatibility and confirmed as a quantifier of incompatibility resources [8]. However, the geometrical property for four parameters disappears because the robustness is defined as the ability of the system to resist noises, which eliminates interaction information among the four parameters.

Therefore, we start to construct a new quantifier of the degree of incompatibility in the QSD scenario. The new quantifier has two desirable properties:

  1. 1.

    It needs to be related or mapped to the geometrical property of the convex model.

  2. 2.

    It needs to be relevant to the noise levels of ensembles prepared by Alice and geometrical distance in the convex model, for example D=S×m, m=rx+ry, where D is the new quantifier, S represents the geometrical distance in the convex model and m is a function of (rx,ry).

In Fig. 2, (sx,sy) and \((s_{x_{0}},s_{y_{0}})\) represent prior- and post-measurement guessing probabilities, respectively. If there exists a new definition of the degree of incompatibility as D, we hope D can satisfy \(D \propto P(s_{x}-s_{x_{0}},s_{y}-s_{y_{0}})\). In this way, we can convert D into a geometrical vector in a two-dimension cartesian coordinate system. Fortunately, considering Eq. (10), it is convenient to construct D satisfying the two requests above:

$$ \begin{aligned} D(r_{x},r_{y},s_{x},s_{y}) &= P^{Prior}-P^{Post} \\ &=\frac{d-1}{2d}\left[r_{x}\left(s_{x}-s_{x_{0}}\right)+r_{y}\left(s_{y}-s_{y_{0}}\right)\right]\\ &=\frac{d-1}{2d}\left[r_{x} \Delta_{x}+r_{y} \Delta_{y}\right]. \end{aligned} $$
(11)
Fig. 2
figure 2

The blue curve represents the boundary W=0 in the plane (sx,sy) varying the value of k and the newly defined D has two forms as Eqs. (11) and (12). a The vector form of D is an effective tool to describe incompatibility by vector connecting equivalent optimal joint measurement \((s_{x_{0}},s_{y_{0}})\) and measurements (sx,sy), which is also able to describe incompatibility between different measurements (sx,sy) and (sx1,sy1) in the case of (rx,ry) fixed. S represents geometrical distance. b The distance form of D is a more intuitive tool to describe incompatibility by distance h between measurements implemented and linear witnesses. All measurements on the parallel of one linear witness have the same degree of incompatibility

Full size image

We call Eq. (11) the vector form of D. In Fig. 2a, (Δx,Δy) represents the vector from PPost to PPrior.

Here we construct a linear map from geometrical space to the quantifier D with coefficients associated with (rx,ry) and the dimension d. Moreover, using this form, we can compare different (sx,sy) under a common given ensembles (rx,ry) by a vector from (sx,sy) to \((s_{x_{1}},s_{y_{1}})\). In addition, if (sx,sy) is exactly at the special point \((s_{x_{0}},s_{y_{0}})\), there appears an interesting phenomenon that compatibility always exists whatever the value of (rx,ry) is, as long as its ratio k is fixed.

Further more, the value of D can be given as

$$ D=\frac{d-1}{2d}\sqrt{r_{x}^{2}+r_{y}^{2}} \times h, $$
(12)

where h is the distance from (sx,sy) to the tangent, which is tangent to the boundary curve in the point \((s_{x_{0}},s_{y_{0}})\).

We call Eq. (12) the distance form of D, which represents the ordinary product of the function of (rx,ry) and the geometrical distance h. In Fig. 2b, the red tangent is actually the LIW with a fixed (rx,ry), and the direction of h represents whether it is incompatible or not. The value |h| can also be linearly mapped into the quantifier D with a coefficient related to the noise levels of ensembles.

Obviously, all points on one parallel of the tangent have a common D, which implies that different (sx,sy) can achieve the same observation. Similarly, the tangent in the point \((s_{x_{0}},s_{y_{0}})\) is the special line, where all points on this line are detected compatible as long as (rx,ry) maintains the fixed ratio k.

In Fig. 2, the region inside convex curve for (sx,sy) represents the observation is compatible regardless of (rx,ry), because no matter what k is, (sx,sy) is always inside the linear witness. But if (sx,sy) is in the region outside the convex curve, the specific question about whether incompatible or not should be considered as two cases of purple and orange points in Fig. 1b.

3.3 Two applications of this framework

The geometrical incompatibility framework provides good tools to describe incompatibility phenomena, which leads to two applications.

For the first application, we consider the case for one who does not care about ensembles in QSD scenario and wants to witness incompatibility between two POVMs. It implies a need to reduce four parameters (rx,ry,sx,sy) to two parameters (sx,sy), which label noisy MUB measurements and are not relevant to ensembles. In this case, we restrict (rx=sx,ry=sy), which means one designs ensembles with the same noise levels as POVMs and in this situation detects incompatibility only depending on the information of given POVMs.

It is easy to prove that the line connecting (rx,ry) and (0,0) is exactly vertical to the corresponding tangent in Fig. 3, which is the LIW of (rx,ry). If a pair of POVMs labeled with (sx,sy) is given, we can obtain the corresponding optimal joint measurement \((s_{x_{0}},s_{y_{0}})\) and D via the following steps. Firstly, We need to draw a line connecting (sx,sy) and (0,0) and draw parallels of its vertical lines. Then, if we find one parallel which is tangent to the convex curve, it is exactly the LIW of (rx=sx,ry=sy), and the tangent point will be the equivalent optimal joint measurement \((s_{x_{0}},s_{y_{0}})\). Finally, the value of D can be obtained via the linear map from (sx,sy), h and d according to Eq. (12).

Fig. 3
figure 3

d=5. In the case (rx=sx,ry=sy,sx,sy), D can be worked out only using geometrical information from the picture, which is an effective and intuitive tool to detect and quantify incompatibility of a pair of POVMs. The olive line connects the (0,0) and (rx,ry). The red line and its parallel represent LIW and they are vertical to the olive line

Full size image

For the second application, we consider the case that POVMs are not noisy MUBs while the ensembles are noisy MUBs, which needs a change in the QSD protocol.

Recalling the protocol, there are three main ingredients for the incompatibility detecting process: (i) a pair of POVMs, whose incompatibility is to be detected, (ii) a pair of ensembles, which are designed to obtain the guessing probability with prior information, and (iii) constructing the optimal joint measurement of ensembles to obtain the guessing probability with post information.

In one word, Alice are requested to design ensembles to obtain \(P_{\text {guess}}^{\text {prior}}\) and \(P_{\text {guess }}^{\text {post}}\) according to POVMs given by Bob. If the case \(P_{\text {guess }}^{\text {post}}<P_{\text {guess}}^{\text {prior}}\) occurs, we can claim that the incompatibility phenomena of the two POVMs appears under the designed ensembles.

If two POVMs E={Ei}i=1,⋯d and F={Fj}j=1,⋯d can recover the labels of two ensembles (A,B) as MUBs, or in another word, can be distinguished by two ensembles as MUBs, satisfying:

$$ \begin{aligned} \text{Tr}\left[E_{m}\left\vert \psi_{m}^{A}\right\rangle\left\langle\psi_{m}^{A}\right\vert\right]&>\text{Tr}\left[E_{m}\left\vert \psi_{i}^{A}\right\rangle\left\langle\psi_{i}^{A}\right\vert \right],i\neq m,\\ \text{Tr}\left[F_{n}\left\vert \phi_{n}^{B}\right\rangle\left\langle\phi_{n}^{B}\right\vert\right]&>\text{Tr}\left[F_{n}\left\vert \phi_{j}^{B}\right\rangle\left\langle\phi_{j}^{B}\right\vert \right],j\neq n. \end{aligned} $$
(13)

Using MUBs as ensembles, we transfer the discrimination of states to the discrimination of POVMs. In this situation, Alice needs to send the information of not only the ensembles but also the labels of the state delivered. Bob does not care about what the density matrixes of (E,F) are but makes sure the probability distribution satisfies Eq. (13).

The prior-measurement guessing probability under ensembles as noisy MUBs is:

$$ \begin{aligned} P_{\text{guess}}^{\text{prior}}=&\frac{1}{2}\left\{\sum_{i}\frac{1}{d}\text{Tr}\left[E_{i}\left(r_{x}\left\vert \psi_{i}^{A}\right\rangle\left\langle\psi_{i}^{A}\right\vert +\frac{1-r_{x}}{d}\mathbb{I}\right)\right] \right.\\&\left.+\sum_{j}\frac{1}{d}\text{Tr}\left[F_{j}\left(r_{y}\left\vert \phi_{j}^{B}\right\rangle\left\langle\phi_{j}^{B}\right\vert +\frac{1-r_{y}}{d}\mathbb{I}\right)\right]\right\}. \end{aligned} $$
(14)

While the post-measurement guessing probability only depends on the ensembles according to Eq. (8). It is natural to convert \(P_{\text {guess}}^{\text {prior}}\) of (E,F) to an equivalent form as \(P(\overline {s_{x}}, \overline {s_{y}})\), which is detailed in Appendix C:

$$ \begin{aligned} \overline{s_{x}}&=\frac{1}{d-1}\left(\sum_{i}\text{Tr}\left[E_{i}\left\vert\psi_{i}^{A}\right\rangle\left\langle\psi_{i}^{A}\right\vert \right]-1\right),\\ \overline{s_{y}}&=\frac{1}{d-1}\left(\sum_{j}\text{Tr}\left[F_{j}\left\vert\phi_{j}^{B}\right\rangle\left\langle\phi_{j}^{B}\right\vert \right]-1\right). \end{aligned} $$
(15)

It is convenient for the POVMs to be rewritten as the form of \(P(\overline {s_{x}}, \overline {s_{y}})\), which implies the geometrical properties also apply for this kind of POVMs.

Here, we change the protocol for detecting the incompatibility of a pair of POVMs. This protocol provides a pair of ensembles as noisy MUB which constitute a convenient ensembles with geometrical information for POVMs to detect or contrast incompatibility. What’s more, the measurements \((\overline {s_{x}}, \overline {s_{y}})\) provide the equivalent \(P_{\text {guess}}^{\text {prior}}\) for (E,F), which implies the same advantage of incompatible POVMs (E,F) to ensembles (rx,ry) as the gap between prior-measurement and post-measurement guessing probability. In this way, we construct a geometrical framework for a kind of POVMs which can be discriminated by MUBs.

3.4 The geometrical framework for quantum incompatibility resources

There are 3 main ingredients for a resource theory [30]: (i) a set of free or resourceless objects, (ii) a set of expensive or resourceful objects, and (iii) a set of allowed transformations between objects, which is supposed unable to create resourceful objects from resourceless objects.

In the geometrical framework, compatible pairs of measurements correspond to the resourceless objects and incompatible pairs correspond to resourceful objects. Then, considering two forms of D, paths of vectors in the convex model carry the information of transformations of quantum incompatibility resources and are linearly mapped into the degree of incompatibility as a quantifier of incompatibility resources.

Obviously, for quantum incompatibility resources in practical QSD tasks, the quantifier D decreases when sharpness (rx,ry) declines maintaining a fixed ratio \(k=\frac {r_{x}}{r_{y}}\). Moreover, for quantum incompatibility between two POVMs under ensembles satisfying (rx=sx,ry=sy), when (sx,sy) decreases and drops inside the convex curve as the olive point in Fig. 1b, the pair of POVMs (sx,sy) is compatible and resourceless, which implies the transformation from expensive objects to free objects which is not able to observe incompatibility phenomena between resourceless objects. It can be seen that D satisfies the three ingredients, and captures the resource of incompatibility.

This advantage of the new framework as a geometrical model is different from the robustness of incompatibility, but they can be linearly correlated with each other in QSD tasks. The robustness of incompatibility in the QSD scenario can be as follows:

$$ 1 + R(A,B) \geq \frac{P^{Prior}}{P^{Post}}. $$
(16)

D can be proven portioned to the lower bound of R in the case of fixed (rx,ry) [8, 18].

4 Conclusion

We construct a geometrical framework for quantum incompatibility resources based on QSD tasks. This framework provides vectors to carry information of transformations for resources, which is also advantageous in describing the incompatibility processes geometrically. We have shown that for incompatible measurements, it is feasible to detect and quantify incompatibility under noisy MUBs with vectors. Furthermore, the geometrical properties in the convex model can be linearly mapped into the quantifier of incompatibility and thus the incompatibility processes, like two applications discussed, are able to be operated intuitively with corresponding vectors. Finally, these properties can be verified by QSD experiments requiring no entanglement.

Our characterization yields a geometrical interpretation of incompatibility resources: the process of incompatibility can be described with geometrical vectors with path information and D is demonstrated as a quantifier of incompatibility resource, which may have potential in other quantum information processes.

Einstein-Podolsky-Rosen steering is related to quantum incompatibility and able to be described in QSD tasks. If two ensembles are compatible, there must exist a local-hidden-state model which implies no steering. And every set of incompatible measurements has the potential of generating EPR steering [8, 31, 32]. These modifications will be an interesting matter of investigation in the case of incompatibility witnesses.

5 Appendix A: Prior- and post-measurement guessing probability

In the two-party system, we have four MUBs labeled with (rx,ry,sx,sy) defined in Eq. (6) and Eq. (5). We set the proportion parameter \(q=\frac {1}{2}\) and mean probability distribution \(p(x)=p(y)=\frac {1}{d}\):

$$ \begin{aligned} P_{guess}^{prior}&=\frac{1}{2}P_{guess}(\mathcal{E}_{X};M)+\frac{1}{2}P_{guess}(\mathcal{E}_{Y};N)\\ &=\frac{1}{2}\sum_{x} p(x) \text{Tr}\left(M_{i} \left(r_{x}\left\vert \psi_{i}^{A}\right\rangle\left\langle\psi_{i}^{A}\right\vert +(1-r_{x}) \mathbb{I} / d\right)\right)\\ &\quad+\frac{1}{2}\sum_{y} p(y) \text{Tr}\left(N_{j} \left(r_{y}\left\vert \phi_{j}^{B}\right\rangle\left\langle\psi_{j}^{B}\right\vert +(1-r_{y}) \mathbb{I} / d\right)\right)\\ &=\frac{1}{2}\left(r_{x}s_{x}+\frac{s_{x}+r_{x}-2r_{x}s_{x}}{d}+\frac{1-s_{x}-r_{x}+r_{x}s_{x}}{d}\right)\\ &\quad+\frac{1}{2}\left(r_{y}s_{y}+\frac{s_{y}+r_{y}-2r_{y}s_{y}}{d}+\frac{1-s_{y}-r_{y}+r_{y}s_{y}}{d}\right)\\ &=\frac{d-1}{2d}\left(r_{x} s_{x}+r_{y} s_{y}\right)+\frac{1}{d}. \end{aligned} $$
(17)

We recall Eq. (7), and write the result as follows:

$$ \begin{aligned} P_{guess}^{post}&=P_{guess}(\mathcal{E};J)\\ &=\sum_{i,j} p(x)p(y) \text{Tr}\left(\left(\frac{1}{2}\Psi_{x}+\frac{1}{2}\Phi_{y}\right)J_{i,j}\right)\\ &=\frac{1}{2}\text{Tr}\left(J_{i,j}\left(r_{x}\left\vert \psi_{i}^{A}\right\rangle\left\langle\psi_{i}^{A}\right\vert +(1-r_{x}) \mathbb{I} / d \right)\right)\\ &\quad+\frac{1}{2}\text{Tr}\left(J_{i,j}\left(r_{y}\left\vert \phi_{j}^{B}\right\rangle\left\langle\phi_{j}^{B}\right\vert +(1-r_{y}) \mathbb{I} / d \right)\right)\\ &=\frac{1}{2}\text{Tr}\left(J_{i,j}\left(r_{x}\left\vert \psi_{i}^{A}\right\rangle\left\langle\psi_{i}^{A}\right\vert \right)\right.+\frac{1}{2}\text{Tr}\left(J_{i,j}\left(r_{y}\left\vert \phi_{j}^{B}\right\rangle\left\langle\phi_{j}^{B}\right\vert \right)\right.\\ &\quad+\frac{1}{2}\text{Tr}\left(J_{i,j}\left(\left(2-r_{x}-r_{y}\right) \mathbb{I} / d\right)\right.\\ &=\frac{r_{x}}{2}\left(b\left(r_{x}+\frac{r_{y}}{d}\right)-c\right)+\frac{r_{y}}{2}\left(b\left(r_{y}+\frac{r_{x}}{d}\right)-c\right)\\ &\quad+\frac{2-r_{x}-r_{y}}{d}[b(r_{x}+r_{y})-2c]\\ &=\frac{1}{4} \sqrt{r_{x}^{2}+r_{y}^{2}-\frac{2d-4}{d} r_{x} r_{y}}+\frac{d-2}{4d}(r_{x}+r_{y})+\frac{1}{d}. \end{aligned} $$
(18)

If we set d=3 and (sx,sy)=(1,1), the results both accord with the experiment result in Ref. [18].

6 Appendix B: Points on the boundary curve

Exploring the geometrical properties in the case of W=0 in Eq. (9), we have:

$$ \begin{aligned} \frac{d-1}{2d}\left(r_{x} s_{x}+r_{y} s_{y}\right)&\!=\frac{1}{4} \sqrt{r_{x}^{2}+r_{y}^{2}-\frac{2d-4}{d} r_{x} r_{y}}+\frac{d-2}{4d}(r_{x}+r_{y}). \end{aligned} $$
(19)

Obviously, it is a function of a straight line for (sx,sy), and if we set \(k = \frac {r_{x}}{r_{y}}\), we will obtain a new form:

$$ \frac{d-1}{2d}\left(k s_{x}+s_{y}\right)\!=\frac{1}{4} \sqrt{k^{2}\!+1-\frac{2d-4}{d} k}+\frac{d-2}{4d}(k+1). $$
(20)

We utilize the intersection of two nearby lines to simulate the boundary curve, and when the variation of k between two lines is small enough, we have:

$$ \begin{aligned} s_{x} &= \frac{2d}{d-1}\frac{\partial \left(\frac{1}{4} \sqrt{k^{2}+1-\frac{2d-4}{d} k}+\frac{d-2}{4d}(k+1)\right)}{\partial k} \\ &=\frac{1}{2(d-1)}\left[ \frac{dk-(d-2)}{\sqrt{k^{2}+1-\frac{2d-4}{d} k}}+(d-2)\right]. \end{aligned} $$
(21)

We can then obtain the form of sx by the function of the straight line:

$$ s_{y}=\frac{1}{2(d-1)}\left[ \frac{d-(d-2)k}{\sqrt{k^{2}+1-\frac{2d-4}{d} k}}+(d-2)\right]. $$
(22)

It is interesting that (sx,sy) here is not directly relevant to the value of (rx,ry), but a function of its ratio k.

7 Appendix C: The equivalent form for a kind of POVMs

For a pair of POVMs can be discriminated by ensembles consisting of noisy MUBs as Eq. (13), we can construct equivalent noisy MUB measurements labeled \(\overline {s_{x}}\) and \(\overline {s_{y}}\) respectively:

$$ \begin{aligned} &\sum_{i}\frac{1}{d}\text{Tr}\left[E_{i}\left(r_{x}\left\vert \psi_{i}^{A}\right\rangle\left\langle\psi_{i}^{A}\right\vert +\frac{1-r_{x}}{d}\mathbb{I}\right)\right]=r_{x}\overline{s_{x}}+\frac{1-r_{x}\overline{s_{x}}}{d},\\ &\sum_{i}\frac{r_{x}}{d}\text{Tr}\left[E_{i}\left\vert \psi_{i}^{A}\right\rangle\left\langle\psi_{i}^{A}\right\vert \right]+\frac{1-r_{x}}{d}=r_{x}\overline{s_{x}}+\frac{1-r_{x}\overline{s_{x}}}{d},\\ &\sum_{i}\frac{1}{d}\text{Tr}\left[E_{i}\left\vert \psi_{i}^{A}\right\rangle\left\langle\psi_{i}^{A}\right\vert \right]=\overline{s_{x}}+\frac{1-\overline{s_{x}}}{d},\\ &\overline{s_{x}}=\frac{1}{d-1}\left(\sum_{i}\text{Tr}\left[E_{i}\left\vert \psi_{i}^{A}\right\rangle\left\langle\psi_{i}^{A}\right\vert \right]-1\right). \end{aligned} $$
(23)

After the same process for \(\overline {s_{y}}\), we convert the \(P_{\text {guess}}^{\text {prior}}\) of (E,F) to an equivalent form as \(P(\overline {s_{x}}, \overline {s_{y}})\).