Non-monotone Exponential Time (NEXT) Model for the Longitudinal Trend of a Continuous Outcome in Clinical Trials

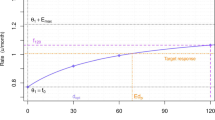
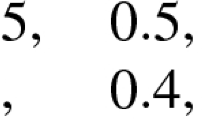Abstract

The dose-response curve has been studied extensively for decades. However, most of these methods ignore intermediate measurements of the response variable and only use the measurement at the endpoint. In early phase trials, it is crucial to utilize all available data due to the smaller sample size. Simulation studies have shown that the longitudinal dose-response surface model provides a more precise parameter estimation compared to the traditional dose response using only data from the primary time point. However, the current longitudinal models with parametric assumptions assume the treatment effect increases monotonically over time, which may be controversial to reality. We propose a parametric non-monotone exponential time (NEXT) model, an enhanced longitudinal dose-response model with greater flexibility, capable of accommodating non-monotonic treatment effects and making predictions for longer-term efficacy. In addition, the estimator for the time to maximum treatment effect and its asymptotic distribution have been derived from NEXT. Extensive simulation studies using known data-generating models and using real clinical data showed the NEXT model outperformed the existing monotone longitudinal models.

Appendix

Proof of the Asymptotic Distribution of the Estimator for $t_p$

The time to maximum treatment effect, $t_p$, can be calculated by solving the following equation

$$\begin{aligned} g(t) = \frac{\partial f(t)}{\partial t} = (\beta _1 +\beta _2 + \beta _1 \beta _2 t) e^{-\beta _1 t} -\beta _2 = 0, \end{aligned}$$

(8)

but it cannot be expressed analytically in a closed form. Therefore, the derivation of the asymptotic distribution of the estimator for $t_p$ is not trivial. Assuming the parameter ${{\varvec{\beta }}}= (\beta _1, \beta _2)'$ can be estimated consistently with

$$\begin{aligned} \sqrt{n} ({\hat{\beta }}-\beta ) \xrightarrow {D} N(0,n\Sigma _{\beta }), \end{aligned}$$

the estimator for $t_p$ can be obtained by solving the equation

$$\begin{aligned} g({{\hat{t}}}_p;\hat{{{\varvec{\beta }}}})=0, \end{aligned},$$

(9)

where

$$\begin{aligned} g({{\hat{t}}}_p; \hat{{{\varvec{\beta }}}})=\frac{\partial f({{\hat{t}}}_p; \hat{{{\varvec{\beta }}}})}{\partial t} = ({{\hat{\beta }}}_1+{\hat{\beta }}_2+{{\hat{\beta }}}_1\hat{\beta }_2 t)e^{-{{\hat{\beta }}}_1 {{\hat{t}}}_p} -{{\hat{\beta }}}_2. \end{aligned}$$

The asymptotic distribution of ${\hat{t}}_p$ can be derived by Taylor expansion on g with respect to t.

$$\begin{aligned} g({\hat{t}}_p,\hat{\beta })= g(t_p,\hat{\beta })+\frac{\partial g(t_p,\hat{\beta })}{\partial t}({\hat{t}}_p-t_p)+O(({\hat{t}}_p-t_p)^2). \end{aligned}$$

Since $g({\hat{t}}_p,\hat{\beta })$ = 0, we have

$$\begin{aligned} {\hat{t}}_p-t_p = - \frac{g(t_p,\hat{\beta })}{g'_{t}(t_p,\hat{\beta })} + O(({\hat{t}}_p-t_p)^2) \end{aligned},$$

(10)

where

$$\begin{aligned} g'_{t}(t_p,\hat{\beta })=\frac{\partial g(t_p,\hat{\beta })}{\partial t} = -\hat{\beta }_1^2 (1+\hat{\beta }_2 t_p)e^{-\hat{\beta }_1 t_p}. \end{aligned}$$

By delta method, we have

$$\begin{aligned} \sqrt{n} \left[ g(t_p,\hat{\beta })-g(t_p,\beta ) \right] \xrightarrow {D} N\left( 0,n[g'_{\beta }(t_p,\beta )]^{T}\Sigma _{\beta }[g'_{\beta }(t_p,\beta )]\right) , \end{aligned}$$

where $\Sigma _{\beta }$ is the variance matrix of $\hat{\beta }$ and

$$\begin{aligned} g'_{\beta }(t_p,\beta )=\frac{\partial g(t_p,\beta )}{\partial \beta }= \left( \begin{array}{c} \frac{\partial g(t_p,\beta )}{\partial \beta _1} \\ \frac{\partial g(t_p,\beta )}{\partial \beta _2} \end{array} \right) = \left( \begin{array}{c} (1-t\beta _1-\beta _1\beta _2t^2)e^{-\beta _1t} \\ (1+\beta _1t)e^{-\beta _1t}-1 \end{array} \right) . \end{aligned}$$

Given $g'_{t}(t_p,\beta )$ is a continuous function, by the Continuous Mapping Theorem, we have

$$\begin{aligned} g'_{t}(t_p,\hat{\beta })\xrightarrow {P} g'_{t}(t_p,\beta ). \end{aligned}$$

Then, by Slutsky’s Theorem, the asymptotic distribution of $\hat{t_p}$ can be written as

$$\begin{aligned} \sqrt{n}({\hat{t}}_p-t_p)=\frac{\sqrt{n}g(t_p,\hat{\beta })}{g'_{t}(t_p,\hat{\beta })} \xrightarrow {D} N(0,n [g'_{t}(t_p,\beta )]^{-2} g'_{\beta }(t_p,\beta )^T \Sigma _\beta g'_{\beta }(t_p,\beta )). \end{aligned}$$

(11)