1 Introduction

Peak current mode (PCM) control has been widely used in power electronic converters due to its accuracy, fast dynamic response and software flexibility [1, 2]. Flying capacitor Buck converters [3], flyback converters [4] and Buck LED drivers [5] are some examples of this PCM control. In full-bridge DC-DC converter applications, PCM control has a simple structure and an inherent built-in overcurrent protection mechanism [6]. Implementation is easy due to the absence of a large inertia filtering link in the current feedback control loop [7]. This also results in the PCM control having a fast response.

In general, PCM control is implemented in cascaded double-loop control structures with the stability mainly depending on the inner current loop. However, when the steady-state duty ratio is higher than 50%, the converters have alternating wide pulses and narrow pulses, namely subharmonic oscillations. These oscillations result in poor system stability. Thus, it is necessary to have an appropriate control [8, 9].

The key to a good PCM control is to accurately model and analyze the characteristics of the current control loop. The numerical calculation in [10,11,12] uses a piecewise linear discrete model to iteratively calculate the circuit response. However, this method, which ignores the influence of parasitic parameters such as the dead-time, and the on–off voltage drop of the switches, is only suitable for simulations. The state space averaging method eases the parameter design for closed-loop controllers [13,14,15,16,17]. However, it is only valid for the low-frequency range below half of the switching frequency. Modeling methods in z-domain [18,19,20] are problematic in terms of high-frequency characteristics since they are based on the same local-averaged state space method. The describing function analysis method in [21] expresses non-linearity with the fundamental component and harmonic components using the Fourier series. However, since the sampling characteristics of the switches are not taken into account, this method cannot illustrate characteristics higher than half of the switching frequency, which are of special importance in the design of high bandwidth controllers. In addition, the aforementioned methods are relatively complicated, which means they are not intuitive enough for practical engineers. Thus, they have limited applications.

The high-frequency characteristics and subharmonic oscillation phenomenon are still less-explored for PCM control in DC-DC converter applications. In this paper, a z-domain modeling method is proposed. By analyzing the small signal step response of the PCM current loop, the geometric constraint relationship between the inductance current and the setting current at each sampling instant is established. Then, the iterative equation of the current and duty cycle are obtained. As a result, the discrete transfer function of the system is derived, which can represent the frequency characteristics above half of the switching frequency. Afterward, the model is converted to the s-domain, so that it is possible to design an appropriate slope compensation to suppress the subharmonic oscillations.

The main contribution of this paper is to propose a z-domain modeling method describing the subharmonic oscillation in the high frequency band, which can explain the instability of the PCM current loop. On the basis of this model, an optimal coefficient adjustment method is provided for slope compensation, which is of great significance to engineering design.

2 Model analysis and current loop modeling

2.1 PCM control system description

A circuit and control diagram of a full-bridge DC-DC converter is shown in Fig. 1. This converter is used for the charging and discharging of a supercapacitor. For the sake of brevity only the charging power flow in the Buck operation mode is investigated, which means the secondary side switches work as if in a synchronous rectifier.

Fig. 1
figure 1

Full-bridge DC-DC converter with PCM control

Full size image

A double closed-loop structure is adopted to control the converter, where PCM control regulates the inner current loop. The control loop includes a voltage feedback compensation network Gc(s), a current comparator, a switching logic control unit, a voltage sensor and a current sensor, where Fv is the voltage feedback coefficient, and Ki is the current sampling transfer function determined by the sensor and the conditioning circuit. The compensated voltage error signal is used to obtain the current loop setting value, and the current comparator is used to modulate the switching duty cycle signal. Then, the average voltage on the inductor is changed by adjusting the turn-on time of the switches.

To simplify the analysis, it is assumed that the transformer is ideal and that the voltages of the DC-bus and the supercapacitor are constant during each switching period. During the steady-state, waveforms of the gate signals and inductance currents can be obtained as shown in Fig. 2.

Fig. 2
figure 2

Steady-state waveforms of a converter in the Buck mode

Full size image

US1–US4 are the driving gate signals for the switches Q1–Q4, IM is the magnetic current, IP is the current of the transformer primary, and IL is the output inductor current.

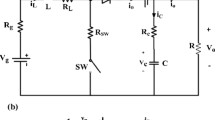
Once the closed loop controller becomes asymptoticly stable, the current loop model in Fig. 1 is equivalent to a simplified PCM circuit in a non-isolated topology as shown in Fig. 3. VD = UD/N is the referred voltage of the DC-bus voltage with respect to the supercapacitor side according to the turns ratio of the transformer, UC is the supercapacitor voltage, L is the inductor, and I2 is the current flowing at the transformer secondary side.

Fig. 3
figure 3

Simplified non-isolated PCM circuit in the Buck mode

Full size image

An ideal waveform of the inductor current is shown in Fig. 4, where Iset is the setting current, Io is the average current, and T is a switching period.

Fig. 4
figure 4

Inductor current according to volt-second balancing

Full size image

The inductor current waveform is continuous. However, its derivative is not equal to 0, and the overall system is not at equilibrium. Therefore, it is a typical nonlinear system. To facilitate the design of the PI controllers, it is necessary to linearize the overall system around its steady-state operation point.

2.2 Traditional linear approximation models

The local-averaging method in [22, 23] is a mainstream modeling method for power electronic converters. Based on the simplified structure diagram in Fig. 3, the first-order approximated current loop model with the inductor current IL as the state variable is established as follows:

$$\dot{I}_{L} = \left( {\frac{{U_{D} }}{NL} - \frac{{U_{C} }}{L}} \right) \cdot D - \frac{{U_{C} }}{L} \cdot \left( {1 - D} \right) = \frac{D}{NL}U_{D} - \frac{{U_{C} }}{L}$$
(1)

Consider the small-signal model IL, D, UD, and UC which are composed of an average value and ripple components:

$$I_{L} = \overline{I}_{L} + \hat{I}_{L} , \, D = \overline{D} + \hat{D}, \, U_{D} = \overline{U}_{D} + \hat{U}_{D} , \, U_{C} = \overline{U}_{C} + \hat{U}_{C}$$
(2)

After substituting (2) into (1) and removing the static values, the nonlinear state model can be established as:

$$\dot{I}_{L} = \frac{{\overline{D} }}{NL}\hat{U}_{D} + \frac{{\overline{U}_{D} }}{NL}\hat{D} - \frac{{\hat{U}_{C} }}{L}$$
(3)

Suppose K1 is the on-time slope of the inductor current. Then, the duty cycle reference in the current loop can be expressed below:

$$D = \frac{{T_{on} }}{T} = \frac{{(I_{set} - I_{L} K_{i} )}}{{T \cdot K_{1} K_{i} }} = (I_{set} - I_{L} K_{i} )G_{1}$$
(4)

where \(G_{1} = \frac{1}{{T \cdot K_{1} K_{i} }},K_{1} = \frac{{V_{D} - V_{C} }}{L}\).

According to (2) and (4), the small signal of the duty cycle in the peak current mode can be the approximately expressed as:

$$\hat{D} \approx \left( {\widehat{I}_{set} - \widehat{I}_{L} K_{i} } \right)G_{1}$$
(5)

From Eqs. (1)–(5), a block diagram of the current loop can be drawn as shown in Fig. 5.

Fig. 5
figure 5

Control block diagram based on the state-space averaging method

Full size image

Therefore, the AC small signal transfer function is as follows:

$$G_{Buck} \left( s \right) = \left. {\frac{{\widehat{I}_{L} (S)}}{{\widehat{I}_{set} (S)}}} \right|_{{\hat{U}_{D} (S) = \hat{U}_{C} (S) = 0}} = \frac{1}{{K_{i} }}\frac{1}{{\frac{NL}{{\overline{U}_{D} G_{1} }}s + 1}}$$
(6)

It can be seen from the transfer function that the system has only one pole in the left half plane and that the system is stable at any duty cycle. However, in actual situations, the inductor current oscillates when D > 0.5. Obviously, Eq. (6) cannot describe this unstable phenomenon.

2.3 Analysis of subharmonic oscillation

Subharmonic oscillation and instability are the two main problems of PCM control [5, 24, 25]. When VC/VD is close to 0.5, the angle between the rising curves of IL and Iset is smaller than the angle between the falling curves of IL and Iset. When there is a disturbance in the input, after a gradual accumulation of disturbances over several switching cycles, the duty cycle of two adjacent switching cycles has one large and one small response, which are asymmetric at the switching frequency [26]. The current loop causes subharmonic oscillation, as shown in Fig. 6.

Fig. 6
figure 6

Time-domain response of a current loop under a sinusoidal disturbance input at half the switching frequency: a VC/VD = 0.25; b VC/VD = 0.5

Full size image

Suppose the current loop input is added to a disturbance signal with an amplitude of one thousandth of the setting current and a frequency of one-half of the switching frequency. When VC/VD is close to 0.5, the current loop exhibits an amplitude amplification at the selective frequency of ½ the switching frequency [27, 28].

This amplification effect can weaken the disturbance suppression capability of the system, reduce the equivalent switching frequency by half, or even lead the system to instability. The results in Fig. 7 show that when the output voltage approaches half the input voltage, a low damping characteristic is exhibited by the signal in the band around the half the switching frequency. In addition, the amplification of the loop amplitude at this frequency increases sharply until it reaches the critical stability condition. In this process, the current loop gradually evolves into an oscillator at half the switching-frequency.

Fig. 7
figure 7

Amplitude-frequency characteristics of GI(Z) with various output-input voltage ratios

Full size image

Phase lag information of the current loop under different input and output conditions is also obtained by frequency-domain analysis.

The bifurcation and oscillation phenomenon in the PCM current loop structure have been explained in [29]. During the process of a proportional increase between the output voltage and the input voltage of a full-bridge DC-DC converter, the steady state of the current loop enters the bifurcation state from the volt-second equilibrium state. Then, the oscillation phenomenon occurs.

3 Stability analysis and slope compensation

3.1 The proposed discrete modeling method

It can be seen from the steady-state operating waveforms of the full-bridge DC-DC converter in Fig. 4, that the rising and falling slopes of the inductor current, the setting current and the current of the starting points at two adjacent switching cycles form a geometric constraint relationship.

Let Iset[n], IL[n], and D[n] be the discretization values of the setting current Iset, the inductor current IL at the start of the sampling period and the duty cycle D during the switching period in the current loop, respectively. Based on the geometric relationship of each variable under the step response, as shown in Fig. 8, a recurrence relationship can be created.

  1. (1)

    Using the tangent theorem of the triangle, the duty cycle D[n] can be calculated by Iset[n], IL[n], and the rising slope of the inductor current.

  2. (2)

    The increment of the inductor current ∆IL[n] during this period is determined by the difference between D[n] and the steady-state duty cycle DDC[n], which is determined by the volt-second balance.

  3. (3)

    By accumulating the values of IL[n] and ∆IL[n] of the present cycle, the inductor current value IL[n + 1] of the next cycle can be derived.

Fig. 8
figure 8

Typical small-signal step response of PCM current control

Full size image

A step response diagram of the current loop operating at a duty cycle of 0.33 is illustrated in Fig. 8. A dynamic structure diagram of this recurrence relation is shown in Fig. 9. Ki is the current feedback constant coefficient in the actual circuit shown in Fig. 1, and ILF[n] is the current feedback signal.

Fig. 9
figure 9

Block diagram for the proposed PCM current control

Full size image

From the geometric relationship of Fig. 8, the duty cycle of each sampling time is:

$$D[n] = (I_{set} [n] - I_{LF} [n])\frac{1}{{K_{1} K_{i} T}}$$
(7)

The incremental change in the inductor current between two sampling instants can be expressed as:

$$\Delta I_{L} [n] = (D\left[ n \right] - D_{DC} \left[ n \right])\frac{{V_{D} }}{L}T$$
(8)

DDC is the steady-state duty cycle determined by the volt-second balancing principle, which results in:

$$K_{1} = \frac{{V_{D} - V_{C} }}{L},D_{DC} \left[ n \right] = \frac{{V_{C} }}{{V_{D} }}$$
(9)

The transfer functions of the overall dynamic structure diagram in Fig. 9 can be obtained according to (7)–(9):

$$G_{1} = \frac{L}{{(V_{D} - V_{C} )K_{i} \cdot T}},G_{2} = \frac{{V_{D} }}{L}T$$
(10)

Therefore, the system shown in Fig. 9 is a simple first-order discrete linear time-invariant system. With the current achieving volt-second balance, the steady-state duty cycle DDC[n] in the structure diagram can be removed to sort out the z-domain small-signal model of the PCM current loop so that the transfer function of GI(Z) can be obtained as follows:

$$G_{I} (Z) = \frac{{G_{1} G_{2} }}{{Z + (G_{1} G_{2} K_{i} - 1)}} = \frac{{\frac{{V_{{\text{D}}} }}{{\left( {V_{D} - V_{{\text{C}}} } \right)K_{i} }}}}{{Z + (\frac{{V_{D} }}{{V_{D} - V_{C} }} - 1)}}$$
(11)

The pole position is used to determine the stability and frequency response characteristics of the current loop on the z-domain. In practice, it is necessary to further manipulate GI(Z) in Eq. (11) by quantifying the frequency domain characteristics in a unit circle of the s-domain to provide a theoretical basis for system stability analysis and oscillation suppression. Therefore, by replacing Z in Eq. (11) with esTs, and multiplying the transfer function of the zero-order sample-hold effect [30], the continuation of the discrete model GI(Z) can be obtained as follows:

$$G_{I} (S) = \frac{{\frac{{V_{D} }}{{\left( {V_{D} - V_{C} } \right)K_{i} }}}}{{e^{{sT_{s} }} + (\frac{{V_{D} }}{{V_{D} - V_{C} }} - 1)}} \cdot \frac{{1 - e^{{ - sT_{s} }} }}{s} \cdot f_{s}$$
(12)

According to the second-order Pade function, esTs can be approximately equal to:

$$e^{{sT_{s} }} \approx \frac{{s^{2} + 6f_{s} s + 12f_{s}^{2} }}{{s^{2} - 6f_{s} s + 12f_{s}^{2} }},\quad \left( {T_{s} = \frac{1}{{f_{s} }}} \right)$$
(13)

Therefore, the s-domain transfer function of the discrete model can be obtained as follows:

$$G_{I} (S) = e^{{ - sT_{s} }} \cdot \frac{k}{{s^{2} + 6f_{s} rs + 12f_{s}^{2} }}$$
(14)

where k = 12fs2/Ki, and r = 1 − 2DDC.

An example using the parameters listed in Table 1 is presented below to show the advantages of the proposed discrete model over the traditional state-space averaging model. Bode diagrams of both models are shown in Fig. 10. When compared with the traditional linear model, the proposed discrete model is more consistent with the actual performance of a system in the high-frequency band.

Table 1 DC-DC converter parameters
Full size table
Fig. 10
figure 10

Bode diagram of the traditional approximation linear model and the proposed discrete model

Full size image

This can be seen more clearly from a spectrum comparison of three current signals after processing by the Chebyshev window as shown in Fig. 11. Among them, IL(t) is the actual inductor current, while ILt(t) and ILd[t] are obtained by the traditional state-space averaging model and the discrete model, respectively.

Fig. 11
figure 11

Spectrum comparison of traditional and discrete methods

Full size image

The spectrum difference between ILd[t] and IL(t) is small within a quarter of the switching frequency. The accuracy of the model is still acceptable when the frequency is close to half the switching frequency since the effect of the duty cycle on the inductor current can be correctly reflected. For practical engineering purposes, it is convenient to carry out the analysis using the traditional approximation. However, the large discrepancy between IL(t) and ILt(t) after half of the switching frequency shows the inherent disadvantages in the traditional state space average method. The spectrum of the inductor current is not well matched and cannot reflect the oscillation at ½ the switching frequency.

3.2 Slope compensation model mechanism

According to the analysis in Sect. 3.1, in order to stabilize the current loop of the system, feedback correction is usually considered to reconfigure the unstable pole of GI(z). For example, the average current mode control in [31] can be used. Slope compensation that superimposes a rising slope signal on the current feedback signal is used to stabilize the PCM current loop [32,33,34,35].

As shown in Fig. 12, Iset is the setting current, IL is the inductor current without disturbances added, ILdb is the inductor current with disturbances added, ∆I0 and ∆I1 indicates the current error at the beginning and end of the period, K1 and K2 are the on-time and off-time slopes of the inductor current (K1 = (VD − VC)/L, K2 = VC/L), Kcp is the compensation slope, and Ts is the switching period.

Fig. 12
figure 12

Current waveforms and slope compensation

Full size image

With the help of slope compensation, the disturbance influence on the current can be suppressed or even eliminated, as shown in Fig. 12. However, it is still not sufficient to explain and solve the problem of subharmonic oscillations.

To address this, it is interesting to analyze the effect of slope compensation. Then, the analytical optimal value of the compensation slope Kcp should be derived by analyzing the z-domain system model presented in Sect. 3.1.

According to Fig. 9 and Eq. (9), the pole of the current loop is:

$$1 - G_{1} G_{2} K_{i} = 1 - \frac{1}{{K_{1} K_{i} }}\frac{{V_{D} }}{L}K_{i} = 1 - \frac{{V_{D} }}{{V_{D} - V_{C} }}$$
(15)

This indicates that instability only depends on the operating points of the input and output voltage, and that it has nothing to do with other parameters, which means that changing the system internal parameters cannot eliminate instability. When the switching device is turned on, the lack of a rise rate causes the gain of the current loop to be too large. Therefore, the crux of the problem is to reduce the loop gain of the current loop without changing the input and output voltage conditions. The solution adopted in this paper is to superimpose a rising slope signal on the current feedback signal, as shown in Fig. 13. In this way, the error at the starting point of the switching cycle results in a lower duty cycle output, which is equivalent to a reduction in the loop gain.

Fig. 13
figure 13

Slope compensation circuit

Full size image

The expressions of the compensated current open-loop gain are as follows:

$$G_{1} G_{2} K_{i} = \frac{1}{{\left( {K_{1} { + }K_{cp} } \right)K_{i} \cdot T}} \cdot \frac{{V_{{\text{D}}} }}{L}T \cdot K_{i} = \frac{1}{{\frac{{V_{{\text{D}}} - V_{{\text{C}}} }}{L} + K_{cp} }}\frac{{V_{{\text{D}}} }}{L}$$
(16)

The condition for system stability is shown below:

$$\left| {G_{1} G_{2} K_{i} - 1} \right| < 1$$
(17)

or:

$$G_{1} G_{2} K_{i} = \frac{{V_{D} }}{{V_{D} - V_{C} + LK_{cp} }} < 2$$
(18)

Therefore, the inequality for the critical compensation condition is:

$$K_{cp} > \frac{{V_{C} - 0.5V_{D} }}{L} = \frac{{\left( {D_{DC} - 0.5} \right)V_{D} }}{L}$$
(19)

If the compensation slope increases to the critical value, the compensation slope is equal to the absolute value of the inductor current falling slope. At this time, Kcp = VC/L and the pole of the current loop are pushed towards the origin of the Z-plane. Then, the current loop becomes a time-delayed first-order system. For step inputs in the range of the small signal, the subharmonic oscillation of the current loop is well suppressed. However, the adjusting time is as long as one switching period, as shown in Fig. 14, where Dcp[n] is the duty cycle with slope compensation.

Fig. 14
figure 14

Current loop step responses with Kcp = VC/L

Full size image

Since the fixed slope rate is not suitable for all of the operating conditions, the compensation slope is parameterized for easy adjustments.

$$K_{cp} = \frac{{\left( {D_{DC} - 0.5 + 0.5X} \right)V_{D} }}{L}$$
(20)

where X is the normalized slope adjustment parameter with a value range of (0, 1]. Accordingly, the range of the slope Kcp is in the range of [(VC − 0.5VD)/L, VC/L]. In these cases, the z-domain small signal transfer function of the PCM current loop can be expressed as follows:

$$G_{d} (Z) = \frac{{G_{1} G_{2} }}{{Z + (G_{1} G_{2} K_{i} - 1)}} = \frac{{\frac{{V_{{\text{D}}} }}{{\left( {V_{D} - V_{{\text{C}}} } \right) + LK_{cp} }} \cdot \frac{1}{{K_{i} }}}}{{Z + \left( {\frac{{V_{{\text{D}}} }}{{\left( {V_{D} - V_{{\text{C}}} } \right) + LK_{cp} }} - 1} \right)}}$$
(21)

To observe the effect of slope compensation, the compensation coefficient X is increased in steps of 0.25. The current loop Bode diagram characteristics for different values of X are shown in Fig. 15.

Fig. 15
figure 15

Current loop amplitude-frequency characteristic with various compensation slopes

Full size image

It is important to note that with an increase of the coefficient X, the damping for the high-frequency signal gradually increases. In addition, the phase shift also increases. In other words, increasing the slope compensation Kcp can improve the stability of the system. However, it also affect the response speed of the system.

Following the analysis in Sect. 3.1, the s-domain expression of Gd(Z) can be obtained by Eqs. (20)-(21) as follows:

$$\left\{ \begin{gathered} G_{d} (S) = e^{{ - sT_{s} }} \cdot \frac{{12f_{s}^{2} }}{{s^{2} + 6f_{s} r_{d} s + 12f_{s}^{2} }} = e^{{ - sT_{s} }} \cdot G_{k} (S) \hfill \\ r_{d} = 1 - \frac{2}{{V_{D} }} \cdot (V_{C} - LK_{cp} ) = X \hfill \\ \end{gathered} \right.$$
(22)

According to Eq. (22), the dynamic performance and the steady-state performance of the system are mainly determined by Gk(S). Therefore, comparing this with a standard second-order system yields:

$$\left\{ \begin{gathered} \omega_{n} = 2\sqrt 3 f_{s} \hfill \\ \xi = \frac{{3f_{s} r_{d} }}{{\omega_{n} }} \hfill \\ \end{gathered} \right.$$
(23)

where ωn is the natural oscillation frequency, and ζ is the damping of the system.

Substituting Eq. (23) into Eq. (22), the normalized slope adjustment parameter X can be calculated as:

$$X = \frac{{\xi \omega_{n} }}{{3f_{s} }} = \frac{2\sqrt 3 }{3} \cdot \xi$$
(24)

In engineering applications, while ensuring the stability of the system, the response speed of the system should be increased as much as possible. Therefore, the damping coefficient ζ for the system is often set to 0.707, which is the optimal damping coefficient.

However, the introduction of the coefficient X brings peak inductor current errors. When X increases, the error increases. As can be seen from Fig. 14, when the slope compensation reaches its maximum value, the actual inductor current cannot approach its reference setting. Therefore, the current setting value needs to be modified according to the slope compensation Kcp together with the steady-state duty cycle D, as shown below:

$$I_{{{\text{set}}}}^{ * } = I_{{{\text{set}}}} + K_{CP} \cdot D \cdot T$$
(25)

After modifying the setting value, the actual peak inductor current is equal to \(I_{{{\text{set}}}}^{*}\). In an ideal case, the error caused by the peak current control can be eliminated.

4 Simulation and experimental results

4.1 Simulation results

A current loop model is built in MATLAB/Simulink to control a full-bridge DC-DC converter working in the Buck mode. The specified parameters set according to an actual system are shown in Table 1. The target inductor current range of the current loop is 0-20A. In this subsection, the effects of the slope compensation on the dynamic and steady-state performances are analyzed by simulations.

In this example, X is chosen as 0.8164 to have the optimal damping coefficient of 0.707. Then, the slope compensation Kcp can be obtained by Eq. (20). The current setting value Iset is modified based on Eq. (25). When the current loop is suddenly set at 20A, the current of systems steps up, and the results are shown in Fig. 16 and Fig. 17.

Fig. 16
figure 16

Current loop step responses under different slope compensation coefficients: a X = − 0.38, Kcp = 0; b X = 0, Kcp = 43,750; c X = 0.8164, Kcp = 212,130; d X = 3, Kcp = 662,500

Full size image
Fig. 17
figure 17

Steady-state current waveforms with different slope compensation coefficients: a X = 0, Kcp = 43,750; b X = 0.8164, Kcp = 212,130

Full size image

With an increase of the slope compensation coefficient X, the subharmonic oscillation phenomenon is gradually suppressed. However, if X is too large, the response speed of the current loop becomes slow, as shown in Fig. 16. When X is equal to 0.8164, the steady-state performance of the current loop is greatly improved. Meanwhile, it also ensures that the system has fast response. This validates the theoretical analysis in Sect. 3, where the system achieves good dynamic and steady-state performances by adding an appropriate slope compensation.

4.2 Experimental results

Experiments were carried out to validate the discrete model and the slope compensation technique. The experimental set-up is shown in Fig. 18. The structure diagram and initial condition settings are shown in Fig. 19. Supercapacitor modular energy storage devices were used as loads at the low-voltage side with the rated voltage being 360 V. The DC-bus supply was used at the high-voltage side, which was made up of an AC power source and a diode rectifier bridge.

Fig. 18
figure 18

Experimental prototype set-up

Full size image
Fig. 19
figure 19

Control structure of the experimental full-bridge DC-DC Buck converter

Full size image

During the experiments, the sampled value of the inductor current was superimposed with a ramp signal, and compared with the setting value, which generates a duty cycle modulation signal. In Fig. 20, CH1 is the ramp signal generated by the ramp circuit according to Kcp, CH3 is the inductor current, CH2 represents the inductor current of the superimposed ramp signal after gain adjustment, and CH4 is the duty cycle signal. The dotted line in the figure indicates the simulated setting value of the inductor current.

Fig. 20
figure 20

Ramp signal and duty cycle waveforms

Full size image

The system was set according to the initial conditions shown in Table 1. When the current loop was suddenly set to 10A, the current of the system steps up, and the experimental waveform is shown in Fig. 21. In this figure, CH1 is the inductor current waveform, CH4 is the primary current waveform, and CH2 and CH3 are the PWM drive signals of the full-bridge module. Due to the addition of the ramp signal, a corresponding peak error was generated, which had been compensated by the correction formula (25).

Fig. 21
figure 21

Step response transient waveforms with different slope compensation coefficients when: a X = 0, Kcp = 43,750; b X = 0.8164, Kcp = 212,130

Full size image

Under the effect of the step response, the system worked in the maximum duty cycle, and the inductor current rose rapidly. However, the subharmonic oscillation phenomenon appeared as shown in Fig. 21a. The optimal value of the slope compensation can be calculated by Eqs. (20), (24), (25) and the corresponding current waveforms are shown in Fig. 21b. When compared with Fig. 21a, it can be seen that the subharmonic oscillation with the new slope compensation was well suppressed. Thus, the inductor current and the primary current were more stable.

Steady-state results are given in Fig. 22 with the same initial conditions. CH1 and CH2 are the PWM drive signals of the full-bridge switches, CH3 is the primary current, and CH4 is the inductor current.

Fig. 22
figure 22

Steady-state waveforms with different slope compensation coefficients in experiments when: a X = 0, Kcp = 43,750; b X = 0.8164, Kcp = 212,130

Full size image

The waveforms in Fig. 22 show that the duty cycles of two adjacent switching cycles have one large and one small response when no slope compensation is added. This is consistent with the analysis in Sect. 3. The presented inductor current and primary current waveforms exhibited subharmonic oscillations, and the transformer emitted significant noise. With the addition of appropriate slope compensation, all of the current waveforms remained stable and the subharmonic oscillations were eliminated.

5 Conclusion

In this paper, a small-signal discrete modeling method was presented and analyzed in the z-domain for the peak-current mode (PCM) control of full-bridge isolated DC-DC Buck converters. This new modeling method can improve the linear approximate accuracy of converters in the high-frequency band above half of the switching frequency when compared with existing local-averaged modeling methods. The new modeling method can be used to explain the instability problem of current control loops. Furthermore, an adjustable slope compensation coefficient has been provided based on the system model in the z-domain, which makes the slope compensation reliable and optimal. Simulation and experimental results have been shown to verify the accuracy of the modeling method, and the capability of the adjustable slope compensation in suppressing the subharmonic oscillations and improving dynamic and steady-state performance.