Non-IID quantum federated learning with one-shot communication complexity

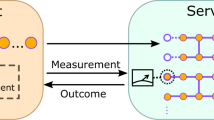
Abstract

Federated learning refers to the task of machine learning based on decentralized data from multiple clients with secured data privacy. Recent studies show that quantum algorithms can be exploited to boost its performance. However, when the clients’ data are not independent and identically distributed (IID), the performance of conventional federated algorithms is known to deteriorate. In this work, we explore the non-IID issue in quantum federated learning with both theoretical and numerical analysis. We further prove that a global quantum channel can be exactly decomposed into local channels trained by each client with the help of local density estimators. This observation leads to a general framework for quantum federated learning on non-IID data with one-shot communication complexity. Numerical simulations show that the proposed algorithm outperforms the conventional ones significantly under non-IID settings.

Appendices

Appendix A. Proof of Proposition 1

Proposition 1 is a quantum generalization of its classical counterpart, Proposition 3.1 in Zhao et al. (2018). Below, we provide a detailed proof following the ideas introduced in Zhao et al. (2018). Based on the definition of Δ and the update rules, Eqs. (2), (3) and (4), we have

$$ \begin{array}{@{}rcl@{}} {\Delta}_{mT} &=& \|w^{(f)}_{mT}-w^{(c)}_{mT}\| = \|\sum\limits_{i} p_{C_{i}} (w^{i}_{mT-1}\\ &&- \eta \nabla_{w} \frac{1}{N_{C_{i}}}\sum\limits_{(|\psi\rangle, y)\in D_{i}}\sum\limits_{k=1}^{n_{c}}\delta_{y, k} f_{k}(w^{i}_{mT-1}, |\psi\rangle))\\ &&- w^{(c)}_{mT-1} + \eta \nabla_{w} \frac{1}{N}\sum\limits_{(|\psi\rangle, y)\in D}\sum\limits_{k=1}^{n_{c}}\delta_{y, k} f_{k}(w^{(c)}_{mT-1}, |\psi\rangle)\| \\ &=& \|\sum\limits_{i} p_{C_{i}} (w^{i}_{mT-1}\\ &&- \eta \sum\limits_{k=1}^{n_{c}}p^{(i)}(y=k) \nabla_{w} \mathbb{E}_{|\psi\rangle|y=k} f_{k}(w^{i}_{mT-1}, |\psi\rangle))\\ &&- w^{(c)}_{mT-1} + \eta \sum\limits_{k=1}^{n_{c}}p(y=k)\nabla_{w} \mathbb{E}_{|\psi\rangle | y=k} f_{k}(w^{(c)}_{mT-1}, |\psi\rangle)\|. \end{array} $$

(13)

Now we apply the triangle inequality and the Lipschitz conditions. Together with the definition $a_{i} = 1 +\eta {\sum }_{k} p^{(i)}(y=k)\lambda _{k}$, we have

$$ \begin{array}{@{}rcl@{}} {\Delta}_{mT} &\le& \|\sum\limits_{i} p_{C_{i}}w^{i}_{mT-1} - w^{(c)}_{mT-1}\| \\ &&+ \eta \| \sum\limits_{i} p_{C_{i}} \sum\limits_{k} p^{(i)}(y=k) (\nabla_{w} \mathbb{E}_{|\psi\rangle|y=k} f_{k}(w^{i}_{mT-1}, |\psi\rangle))\\ &&- \nabla_{w} \mathbb{E}_{|\psi\rangle | y=k} f_{k}(w^{(c)}_{mT-1}, |\psi\rangle))\| \\ &\le& \sum\limits_{i} p_{C_{i}} (1+\eta \sum\limits_{k} p^{(i)}(y=k)\lambda_{k}) \| w^{i}_{mT-1} - w^{(c)}_{mT-1} \| \\ &=& \sum\limits_{i} p_{C_{i}} a_{i} \| w^{i}_{mT-1} - w^{(c)}_{mT-1} \|. \end{array} $$

(14)

Then we continue going backwards in the time steps. With the triangle inequality and the definitions of g(w) and EMD_i, we have

$$ \begin{array}{@{}rcl@{}} &&\| w^{i}_{mT-1} - w^{(c)}_{mT-1} \|\le \| w^{i}_{mT-2} - w^{(c)}_{mT-2}\|\\ &&+ \eta \| \sum\limits_{k} p^{(i)}(y=k) \nabla_{w} \mathbb{E}_{|\psi\rangle|y=k} f_{k}(w^{i}_{mT-2}, |\psi\rangle))\\ &&- \sum\limits_{k} p(y=k) \nabla_{w} \mathbb{E}_{|\psi\rangle|y=k} f_{k}(w^{(c)}_{mT-2}, |\psi\rangle))\| \end{array} $$

$$ \begin{array}{@{}rcl@{}} &\le& \| w^{i}_{mT-2} - w^{(c)}_{mT-2}\| \\ &&+ \eta \| \sum\limits_{k} p^{(i)}(y=k) \nabla_{w} \mathbb{E}_{|\psi\rangle|y=k} f_{k}(w^{i}_{mT-2}, |\psi\rangle))\\ &&- \sum\limits_{k} p^{(i)}(y=k) \nabla_{w} \mathbb{E}_{|\psi\rangle|y=k} f_{k}(w^{(c)}_{mT-2}, |\psi\rangle))\| \\ &&+ \eta \|\sum\limits_{k} (p^{(i)}(y=k)-p(y=k))\mathbb{E}_{|\psi\rangle|y=k} f_{k}(w^{(c)}_{mT-2}, |\psi\rangle)) \| \\ &\le& a_{i}\| w^{i}_{mT-2} - w^{(c)}_{mT-2}\| + \eta g(w^{(c)}_{mT-2})\text{EMD}_{i}. \end{array} $$

(15)

By induction and the broadcast rule $w^{i}_{(m-1)T} = w^{(f)}_{(m-1)T}$, we arrive at

$$ \begin{array}{@{}rcl@{}} \| w^{i}_{mT-1} - w^{(c)}_{mT-1} \| &\le& a_{i}^{T-1}\| w^{i}_{(m-1)T} - w^{(c)}_{(m-1)T} \|\\ &&+ \eta \text{EMD}_{i} \sum\limits_{j=0}^{T-2}{a_{i}^{j}} g(w^{(c)}_{mT-2-j}) \\ &=& a_{i}^{T-1}{\Delta}_{(m-1)T}\\ &&+ \eta \text{EMD}_{i} \sum\limits_{j=0}^{T-2}{a_{i}^{j}} g(w^{(c)}_{mT-2-j}) \end{array} $$

(16)

Plug it into Eq. (14), and we finally reach the desired result:

$$ \begin{array}{@{}rcl@{}} {\Delta}_{mT} &\le& \sum\limits_{i} p_{C_{i}} {a_{i}^{T}} {\Delta}_{(m-1)T} \end{array} $$

(17)

$$ \begin{array}{@{}rcl@{}} &&+ \eta \sum\limits_{i} p_{C_{i}} \text{EMD}_{i} \sum\limits_{j=1}^{T-1}{a_{i}^{j}} g(w^{(c)}_{mT-1-j}). \end{array} $$

(18)

Appendix B. Proof of Theorem 1

With the definitions in Sections 2.1 and 2.4, for any pure input state $\sigma _{x}^{\psi } = |\psi \rangle \langle \psi |$, the global channel ${\mathscr{M}}$ can be decomposed into

$$ \begin{array}{@{}rcl@{}} \mathcal{M}\left( \sigma_{x}^{\psi}\right) &=& \mathcal{M}\left( \frac{P_{x}^{\psi}\rho_{x} P_{x}^{\psi}}{\text{Tr}(\rho_{x} P_{x}^{\psi})}\right) = \mathcal{M}\left( \frac{P_{x}^{\psi}\text{Tr}_{C}(\rho) P_{x}^{\psi}}{\text{Tr}(\rho_{x} P_{x}^{\psi})}\right) \\ &=&\frac{1}{\text{Tr}(\rho_{x} P_{x}^{\psi})}\sum\limits_{i}\mathcal{M}(P_{x}^{\psi} \text{Tr}_{C}(P_{C_{i}} \rho P_{C_{i}} ) P_{x}^{\psi}) \\ &=&\frac{1}{\text{Tr}(\rho_{x} P_{x}^{\psi})}\sum\limits_{i}\mathcal{M}(\text{Tr}_{C}(P_{x}^{\psi} \rho_{x|C_{i}} P_{x}^{\psi})) \text{Tr}(\rho P_{C_{i}}) \\ &=&\frac{1}{\text{Tr}(\rho_{x} P_{x}^{\psi})}\sum\limits_{i}\mathcal{M}_{i}(\sigma_{x}) \text{Tr}(\rho_{x|C_{i}} P_{x}^{\psi}) p_{C_{i}} \\ &=& \sum\limits_{i}\mathcal{M}_{i}(\sigma_{x}) \frac{\mathcal{D}_{i}(\sigma_{x}) p_{C_{i}}}{{\sum}_{j} \mathcal{D}_{j}(\sigma_{x}) p_{C_{j}}}, \end{array} $$

(19)

where the second line utilizes the fact that ρ is diagonal in |C_i〉: $\rho = {\sum }_{i} P_{C_{i}} \rho P_{C_{i}}$, and the last equality follows from

$$ \begin{array}{@{}rcl@{}} &\text{Tr}(\rho_{x} P_{x}^{\psi}) = \text{Tr}(\rho P_{x}^{\psi})={\sum}_{j} \text{Tr}(P_{C_{j}}\rho P_{C_{j}} P_{x}^{\psi}) \\ &= {\sum}_{j} \text{Tr}(\rho_{x|C_{j}} P_{x}^{\psi})\text{Tr}(\rho P_{C_{j}})={\sum}_{j} \mathcal{D}_{j}(\sigma_{x})p_{C_{j}} \end{array} $$

(20)

As for mixed states, we note that they can always be decomposed into a linear combination of pure states. Thus following from the linearity of quantum channels, the formula for ${\mathscr{M}}$ acting on mixed states follows from direct linear superposition. This completes the proof of Theorem 1.

Appendix C. A proposal of quantum generative learning with qFedInf

We mentioned in the main text that the proposed framework qFedInf may be applied to machine learning tasks beyond classification. Here we provide a specific example of performing quantum generative learning (Gao et al. 2018; Lloyd and Weedbrook 2018; Liu and Wang 2018) with qFedInf. This only serves as a preliminary proposal and we leave the detailed study of its performance and implications to future works.

In quantum generative learning, we aim to learn a generative model that can reconstruct some target quantum state ρ_x. In a federated learning context, each client C_i only has access to a small proportion of the total data, which statistically forms a quantum state $\rho _{x}^{C_{i}}$. Thus the whole target state can be written as $\rho _{x} = {\sum }_{i} p_{C_{i}} \rho _{x}^{C_{i}}$, where $p_{C_{i}}$ is the proportion of data accessible to client C_i. The notations here are the same as in Section 2.1.

We take the quantum generative adversarial network (qGAN) (Lloyd and Weedbrook 2018) as our quantum channel ${\mathscr{M}}$ to perform the learning task. It’s a quantum circuit that takes some fixed initial state, for example |0⋯0〉, as its input, and outputs a quantum state, which is parameterized by the circuit parameters. Adversarial learning strategies are applied to train the circuit and the output state after training is expected to approximate the target state. Here we omit the training details as our focus is on the federated learning aspect.

In the qFedInf framework, each client trains its own qGAN, denoted as the local channel ${\mathscr{M}}_{i}$, with its own data $\rho _{x}^{C_{i}}$. After training, we expect ${\mathscr{M}}_{i}(|0\cdots 0\rangle \langle 0\cdots 0|)\approx \rho _{x}^{C_{i}}$. As for the density estimation part, we note that the input states are fixed to be |0⋯0〉, so the density estimators become trivial, i.e., $\mathcal {D}_{i}(|0\cdots 0\rangle )=1$. Plug these into Eq. (11) and we arrive at

$$ \mathcal{M}(|0\cdots0\rangle\langle0\cdots0|) \approx \sum\limits_{i} p_{C_{i}} \rho_{x}^{C_{i}} = \rho_{x}, $$

(21)

which is exactly our goal. This is a concrete proposal of quantum federated generative learning which has not appeared in the literature so far.