1 Introduction

The effect of the increasing concentration in atmospheric greenhouse gases on the global climate system is simulated by Global Climate Models (GCMs). These models have coarse resolutions which make it difficult to meet the requirement of many users demanding high-resolution outputs to produce regional to local-scale climate projections as well as climate impact studies [1]. To address the limitations, various GCM models (e.g. the Coupled Model Intercomparison Project 5 (CMIP5) models) have been dynamically downscaled regionally as Regional Climate Models (RCMs), while others developed different bias-correction methods.

Previous studies have evaluated the use of different model refinement, dynamical and statistical downscaling techniques in various parts of the world, e.g. in the USA and Europe [2,3,4]. Other studies have analysed regional-scale model discrepancies [5,6,7]. However, model biases vary for different regions, thereby making it difficult to draw a definite conclusion as to which model or statistically downscaling and bias correction methods perform best. Hence, there is a need to evaluate the performances of different downscaling and bias-correction methods in different regions.

Various bias-correction (BC) algorithms have been developed [8,9,10], other studies evaluated the performances of the BC algorithms [11, 12], while others expatiated on their limitations [13,14,15]. One of the most widely used bias-correction approaches in climatology is the univariate quantile mapping approach which aims at mapping the source distribution quantiles to target distribution quantiles. Grillakis et al. [16] presented a trend-preserving method based on quantile mapping bias-correction of climate modelled temperature over Europe. This method preserves the standard deviation, the long-term signal in the model mean, and the lower and higher percentiles of temperature. Hempel et al. [9] presented a trend-preserving BC method in the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP). Various studies [17, 18] have used the trend-preserving univariate bias-correction methods such as equidistant quantile matching and quantile delta mapping methods.

However, just like other bias-correction methods, quantile mapping has been used in correcting biases in individual climate variables, thereby disregarding the dependencies and correlation between different variables [7, 19]. Since these dependencies are ignored in univariate BC methods, biases inherent in the dependence structure can affect further analyses making use of multiple variables (e.g. drought monitoring, hydrological modelling) [20]. To preserve this dependency, the multivariate BC methods have been developed [21,22,23,24]. These bias-correct multiple variables concurrently either by considering the whole multivariate dependence structure [22, 24] or assuming stationarity in the temporal sequence of model variables [21].

In the Komadugu-Yobe Basin (KYB), Adeyeri et al. [7] reported a significant positive trend in warm spell duration, warm day-, and warm night frequencies over the Komadougu-Yobe Basin (KYB) using the bias-corrected model output from univariate empirical quantile mapping technique. They also predicted more frequent extreme temperature events in the future. Adeyeri et al. [25] showed that heavy precipitation intensity in the KYB is boosted by temperature increase. This accelerates moisture convergence at low levels which drives the precipitation event. The consequence of the heavy precipitation intensity is more river discharge and subsequent flood events in the basin.

Even though studies involving bias-correction of climate models in the basin are limited, it is unknown if the previous methodologies adopted in bias-correcting climate models preserves the climate signals and the joint dependence structure of the climate variables in the different climatic zones of the basin.

Therefore, this study compares multiple bias-correction techniques using eight GCMs-RCM for the historical period (1975–2005) and future (2020–2050) for annual, dry (December to March) and wet periods (June to September [26]). However, due to the temporal limitation of the observed data, the historical period is further divided into calibration (1975–1990) and validation (1991–2005) periods. The objective of this study is to assess the performance of two univariate and three multivariate BC methods in reproducing the observed maximum temperature distribution as well as the temperature variability over the KYB using eight GCMs-RCM and the mean of the original GCMs-RCM simulation (model ensemble mean) at the historical and future period under representative concentration pathway (RCP) 4.5 and 8.5 scenarios.

2 Study area

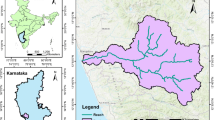
The Komadugu-Yobe Basin (KYB) is a sub-basin of the Lake Chad Basin. It is a transboundary basin shared by Nigeria and Niger Republic. The basin is positioned to the south of the Sahara Desert of Africa with an area of 150,000 km2 (Fig. 1) which is approximately 35% of the Lake Chad Basin. Its elevation varies between 285 and 1750 m [27]. The water losses from the basin are majorly through infiltration, evaporation and irrigation. The average annual precipitation ranges from 300 to 1200 mm [28]. The average annual maximum air temperature varies from 28 to 36 °C, while the minimum air temperature varies from 15 to 22 °C [7]. The KYB houses some valuable wetlands which are significant to both national and international communities because they are sources to some rivers feeding the Lake Chad Basin [28]. The occurrence of three drought periods and recent flood events has called for appropriate adaptation and mitigation practises to combat climate change and extremes in the basin. This requires a good understanding of the present climate considering the past climate events as well as having a good projection into the future, for proper planning.

Fig. 1
figure 1

Map of the study area

Full size image

3 Data and methods

The analyses utilise the observed maximum temperature, minimum temperature, air temperature and precipitation data series for fourteen stations from 1975 to 2005, archived by the Direction de la Meteorologie Nationale (DMN) of the Niger Republic and Nigeria Meteorological Agency (NiMet) (Table 1). The quality control and homogenization processes of the daily maximum temperature data follow the methodology described in Domonkos and Coll [29] and Adeyeri et al. [7, 25]. These data are used as a reference to correct the biases in eight GCMs-RCM and their ensemble mean, obtained from the Coordinated Regional Climate Downscaling Experiment (CORDEX) (Table 2). These GCMs are downscaled dynamically by the Swedish Meteorological and Hydrological Institute-Rossby Centre Atmosphere model version 4 (RCA4) RCM. RCA4 has a resolution of 0.44° × 0.44° with an embedded Bechtold Kain-Fritsch convection scheme. Additional information about the domain setup, physical parameterizations and boundary conditions are described in Samuelsson et al. [30]. This RCM has been proven to perform well in replicating some climate extreme indices over the basin [7]. Point-scale bias-correction of the GCMs-RCM is based on the fourteen stations during the historical period (1975–2005). The historical period is further divided into calibration (1975–1990) and validation (1991–2005) periods. The point-scale precipitation series was extracted from the GCMs-RCM grid using the first-order conservative remapping technique [31,32,33], while the temperature series was extracted using the nearest neighbourhood remapping technique [33]. Subsequently, the station points were extracted from the GCMs-RCM grid for the future (2020–2050) under RCP 4.5 and 8.5. RCP 4.5 is the carbon dioxide emission scenario at 650 ppmv, while RCP 8.5 is the carbon dioxide emission at 1370 ppmv.

Table 1 List of climatic stations
Full size table
Table 2 List of GCMs used as boundary conditions for the Rossby Centre Regional Atmospheric (RCA) model
Full size table

3.1 Bias-correction techniques

Bias-correction (BC) minimizes discrepancies between observed and simulated climate variables. Therefore, this study compares the performances of five BC techniques, namely univariate empirical quantile mapping (EQM), univariate parametric quantile mapping (PQM), multivariate bias-correction method using N-dimensional probability density function transform (MBCN), multivariate bias-correction method using Spearman rank correlation dependency (MBCR) and multivariate bias-correction method using Pearson correlation dependency (MBCP).

For the univariate BC, two quantile mapping techniques are applied to the daily maximum temperature variable. Quantile mapping (QM) is a quantile dependent correction function between the model simulation quantiles and the observation quantiles. This function translates the simulated data into bias-corrected data. However, the assumption here is that models can accurately project the variable’s ranked categories (the quantiles), i.e. the same probability distribution for both historical and future period [34]. These quantiles can either be fitted based on empirical (e.g. Déqué et al. [34]) or parametric distribution (e.g. Piani et al. [12]). In the empirical QM, changes in the model’s Cumulative Distribution Function (CDF) during the calibration and future periods are calculated quantile by quantile. The changes are further rescaled based on the CDF during calibration before adding it, quantile by quantile to the observed quantile, to get a newly calibrated CDF for the future period with exhibited climate change signal (Amengual et al. [35]), while the parametric QM assumes that both model and observation intensity distributions are well approximated by a given distribution. This follows a theoretically fitted distribution. Specifically, the QM transformation can be expressed as follows [7]:

$$ S = k\left( C \right) $$
(1)

where S is the daily observed time series, k is the transfer function and C is the CORDEX time series having the distribution of S.

For a known series distribution,

$$ S = F_{O}^{ - 1} \left( {F_{s} \left( C \right)} \right) $$
(2)

where \( F_{s} \) is the CDF of C and \( F_{O}^{ - 1} \) is the inverse CDF of S.

On the other hand, the multivariate BC uses the QM approach in adjusting the marginal distributions of the climate model simulations while conserving the projected changes in the simulated quantiles. The multivariate rescaling technique is used to adjust the joint multivariate dependency structure [18]. For the multivariate BC, three multivariate techniques (MBCN, MBCR and MBCP) are applied to the maximum temperature variable.

The MBCN [23] is a multivariate equivalent of the univariate quantile delta mapping (QDM) in which all characteristics of the observed distribution are reassigned to the simulations.

In QDM, the observed values are multiplied by the ratio of the modelled values at the same quantiles. The relative or absolute quantile changes between the calibration and future periods are calculated. Thereafter, the bias-corrected future projection is obtained by multiplying these relative changes by the bias-corrected values during the calibration period. This preserves the relative or absolute quantile changes.

The QDM transfer function is given as;

$$ \tilde{X}_{P} \left( i \right) = F_{T}^{ - 1} \left( {F_{P} \left( {X_{P} \left( i \right)} \right)} \right) + \Delta \left( i \right) $$
(3)
$$ \Delta \left( i \right) = X_{P} \left( i \right) - F_{S}^{ - 1} \left( {F_{P} \left( {X_{P} \left( i \right)} \right)} \right) $$
(4)

where \( X_{S} , X_{P} \) and \( X_{T} \) are the historical climate model simulations, climate model projections and historical observations, respectively. \( F_{S} , F_{P} \) and \( F_{T} \) are the CDF of the historical climate model simulations, climate model projections and historical observations, respectively. \( \Delta \left( i \right) \) is an operator which preserves the relative changes in quantiles.

The MBCN extends the N-dimensional probability density function transform algorithm with QDM and works with data from \( X_{S} , X_{P} \) and \( X_{T} \). It rotates the \( X_{S} , X_{P} \) and \( X_{T} \) and applies the absolute change from Eq. (3) to each rotated \( X_{S} , X_{P} \) and \( X_{T} \) variables. Subsequently, the rotated \( X_{S} , X_{P} \) and \( X_{T} \) are rotated back as \( X_{S}^{{\left[ {j + 1} \right]}} ,X_{P}^{{\left[ {j + 1} \right]}} , X_{T}^{{\left[ {j + 1} \right]}} \). This process is repeated until \( X_{S}^{{\left[ {j + 1} \right]}} \) matches \( X_{T} \). To preserve the trends in \( X_{P} \), each column of \( X_{P} \) elements is ordered based on the ordinal ranks of the corresponding elements of each column of \( X_{P}^{{\left[ {j + 1} \right]}} \). Whilst the convergence of MBCN depends on iteratively rotating matrices randomly, the influence of this random rotation is examined through the convergence speed of multivariate distribution using the energy distance [36]. The details of this method are presented in Canon [23]. Conversely, MBCR and MBCP [24] match ranked correlation dependence structure using multivariate linear rescaling and subsequently match the marginal distributions using univariate transformations. The corrected dependence structure is measured either by Spearman rank correlation or Pearson correlation. In both cases, the ranked correlation dependence structure is aligned with the observations. Here, the sequence of the original model output is preserved because MBCP and MBCR sequence modification is quite small.

Nevertheless, in all three multivariate BC methods, the marginal distributions are adjusted based on the change-preserving QDM technique [18].

For this study, the multivariate BC of maximum temperature relies on the observed maximum temperature, minimum temperature, air temperature and precipitation data series at both annual and seasonal time scales.

3.2 Evaluation, trend and interpolation

The performance of the BC methods in replicating the observed maximum temperature distribution is assessed by ranking each method using a comparative model skill score (MSS) [37] for all models with the ensemble mean. This calculates the space–time statistics. The time statistics is derived by comparing and quantifying the phase errors of the space-averaged values time series, while the space statistics is based on the time-average of the study area (Fig. 1) [37]. Thereafter, the MSS is derived from the sum of the normalised \( (Y_{\text{norm}} ) \) values of space (S) and time (t) correlation (r), bias (B), mean absolute error (MAE) and the index of agreement (d) [38].

$$ Y_{\text{norm}} = \frac{{Y_{i} - Y_{ \hbox{min} } }}{{Y_{ \hbox{max} } - Y_{ \hbox{min} } }} $$
(5)

where 0 ≤ \( Y_{\text{norm}} \le 1 \); Y is the space or time-averaged r, B, MAE or d. Ymax and Ymin are the best and worst performance index from all model simulations.

Therefore, MSS is expressed as;

$$ \begin{aligned} {\text{MSS}} = \left( {Sr_{\text{norm}} + \left[ {1 - S\left| B \right|_{\text{norm}} } \right] + \left[ {1 - {\text{SMAE}}_{\text{norm}} } \right] + Sd_{norm} } \right. \\ & \quad \left. { + tr_{\text{norm}} + \left[ {1 - t\left| B \right|_{\text{norm}} } \right] + \left[ {1 - {\text{tMAE}}_{\text{norm}} } \right] + td_{\text{norm}} } \right) \times 100 \\ \end{aligned} $$
(6)

High values MSS denotes good performance, while low values denote bad performance.

The trend in the observation and BC model maximum temperature data series are analysed at annual, wet and dry periods. The trend detection follows the Mann–Kendall (modified Mann–Kendall) description as presented in Adeyeri et al. [27]. Additionally, the results from the pointwise bias-corrected GCMs-RCM were interpolated across the entire basin using ordinary kriging method [39, 40].

4 Results

4.1 Performance evaluation of different BC methods for correcting maximum temperature distribution

Climate models exhibit biases due to systematic model errors, spatial averaging and discretization within grid cells. This is further buttressed in the empirical CDF plot of the uncorrected climate models against the stations’ observed temperature (supplementary file, Fig. S1). The distribution of the models varies greatly from the observation. For example, 20% of the observations have temperature value of 30.00 °C, while at least 90% of climate model outputs have temperature values of 30.00 °C. Hence, there is a need to correct these biases and evaluate the performances of the adopted bias-correction methods (supplementary file, Fig. S2). To evaluate the ability of the different BC methods in correcting the maximum temperature in the study area, three statistical validation measures are adopted (Eq. 6). The results of the models’ comparative performance scores for both calibration and validation periods are presented in Tables 3 and 4a, b and c for annual, dry and wet periods, respectively. The performance scores differ for individual GCMs-RCM and also differ for each BC methods. For example, in the annual series, the performance score during the calibration period is highest for MIROC using EQM and PQM BC methods (90%). However, the BC methods exhibit acceptable performance scores, ranging from 83.4% (MOHC-MBCR) to 90% (MIROC-PQM, EQM) (Table 3a).

Table 3 Comparative performance scores (%) for the basin during the calibration period
Full size table
Table 4 Comparative performance scores (%) for the basin during the validation period
Full size table

The performance scores for the BC methods during the dry season (Table 3b) range between 70.3% (ENS-MBCR) and 88.1% (MPI-MBCN). The range for the wet season is between 68.8% (CNRM-MBCN) and 89.1% (ENS-PQM, EQM). Comparing the percentage bias of the model ensemble mean, using different BC methods for example, during the dry season for the calibration period (Fig. 2 ) shows that EQM, PQM and MBCN have the lowest percentage bias of between 1 and − 4%. The MBCP has the highest range of between − 4 and 21%. The highest range of bias is seen in the uncorrected (raw) model ensemble mean with values between − 14 and 21%. For the annual period (Fig. S3), all BC methods show percentage bias of between − 2 and 2%. For the wet season (Fig. S4), EQM, PQM and MBCR have the lowest range of percentage bias of from 0% to 2%, 0% to 2% and 0% to − 2%, respectively.

Fig. 2
figure 2

Percentage bias (%) in model ensemble mean for dry season temperature for calibration period (1975–1990) for a raw and the different BC methods (b–f). Positive and negative bias means overestimation and underestimation, respectively

Full size image

For the validation period, the performance scores (Table 4) show acceptable performances for the annual period. The MBCN performs best for the dry season, while there are mixed performances for the wet period with CNRM-EQM having the best performance of 87.2%. For percentage bias (Fig. 3), taking the model ensemble mean as an example, the MBCN has the lowest percentage bias of between 0 and − 2%. The performances for other seasons are reported in the supplementary file (Figs. S4–S6).

Fig. 3
figure 3

Percentage bias (%) in model ensemble mean for dry season temperature for calibration period (1991–2005) for a raw and the different BC methods (b–f). Positive and negative bias means overestimation and underestimation, respectively

Full size image

In general, the performance of each model and the BC method varies with season. However, both univariate BC perform well for all seasons during the calibration and validation periods. For multivariate BC, MBCN performs best during the dry season for all models, while MBCR performs best for the wet season. There are mixed performances between the multivariate BC and the models for the annual period.

4.2 Joint dependency structure

To examine the ability of the BC methods in observing the joint dependency structures between the variables considered, the RMSE result between the observed and BC output Spearman maximum and minimum temperature correlation for the model ensemble mean is calculated over all stations considering the entire evaluation period. As an example, Fig. 4a shows that the global RMSE values for the correlation coefficients between mean annual maximum and minimum temperature are identical for all multivariate BC methods with values between 0 and 0.1. The Spearman correlation coefficient ranges between 0.4 and 0.5 for EQM, between 0.35 and 0.45 for PQM and between 0.2 and 0.5 for the uncorrected model ensemble mean. The high RMSE values show that the univariate BC methods are unable to reproduce the observed joint dependency structure between the variables, while the low RMSE values for multivariate BC methods show the strength of these methods in representing the joint dependencies. This same pattern is recorded for the Spearman correlation between maximum temperature and precipitation (not shown).

Fig. 4
figure 4

a Boxplots of RMSE values for the correlation coefficients between mean annual maximum and minimum temperature between 1975 and 2005. b Rates of convergence of MBCR and MBCP for bias-correction of annual maximum and minimum temperature and absolute errors w.r.t. the observation

Full size image

Although the multivariate BC of maximum temperature relies on observed maximum temperature, minimum temperature, air temperature and precipitation data series, it is noteworthy that the convergence of MBCR and MBCP (based on ranked correlation dependence structure) to the targeted multivariate distribution occurs quickly (Fig. 4b). Contrariwise, the MBCN is based on iteratively rotating matrices randomly, whose convergence speed to the targeted multivariate distribution is evaluated using the energy distance. To measure the consequence of the random rotation matrices on the model, the energy distances are evaluated for the uncorrected and BC climate model using MBCN, following 100 iterations and 50 trials (Fig. S7). Convergence rates differ for different models with respect to the energy scores. For example, convergence occurs quickly for MPI, MIROC and ENS after 25 iterations with smaller energy distances, while the random rotations for NCC are suppressed after 80 iterations and at bigger energy distances. This shows that NCC is affected more by these random rotations, hence a need for more iterations.

4.3 Monthly variability of domain’s average temperature

The temporal distribution and comparison of temperature over the basin for the entire historical period (1975–2005) using the univariate BC methods are presented in Fig. 5. The comparison between the observation (Fig. 5a) and the uncorrected model ensemble mean (Fig. 5b) shows no match as the uncorrected model constantly underestimates temperature for all months and years. The EQM (Fig. 5c) performs well in hot months but either underestimates or overestimates in months with low temperature. The PQM (Fig. 5d) performs relatively well in replicating the monthly variability; however, there are little overestimations in months with low temperatures. For multivariate BC methods (Fig. 6), all methods represented the hottest months relatively well. Nonetheless, there are some underestimations in months with low temperature. In all cases, PQM and MBCN replicate the monthly variability satisfactorily.

Fig. 5
figure 5

Monthly variability of basin’s maximum temperature (°C) over the KYB. a Observation. b Uncorrected model ensemble mean. c Corrected model ensemble mean using univariate empirical quantile mapping. d Corrected model ensemble mean using univariate parametric quantile mapping

Full size image
Fig. 6
figure 6

Monthly variability of basin’s maximum temperature (°C) over the KYB. a Observation. b Corrected model ensemble mean using multivariate N-dimensional probability density function transform. c Corrected model ensemble mean using multivariate Spearman rank correlation dependency. d Corrected model ensemble mean using multivariate Pearson correlation dependency

Full size image

4.4 Spatial distribution of temperature variability

Figure 7 presents the result of the spatial distributions of the dry season temperature over the basin. The temperature increases (except the uncorrected model (Fig. 7b)) from the south-western part of the basin to the north-eastern corner, with the lowest temperature range of between 28.70 and 32.10 °C and highest temperature range of between 33.80 and 35.50 °C. Although some parts of the study area are overestimated especially by MBCP and MBCN, conversely, PQM replicates the spatial pattern satisfactorily. The multivariate methods overestimate by at least 1.70 °C in the Sahelian parts of the basin. However, the coldest part of the basin is accurately replicated. For the wet season (Fig. S9), there is an evident latitudinal temperature increase across the basin with temperatures ranging from 25.30 to 37.90 °C. Nevertheless, there is an overestimation of over 1 °C by EQM method in the Sahelian end of the basin. For all seasons, the uncorrected model ensemble mean underestimated the basin’s temperature, while the PQM and MBCN perform well for univariate and multivariate BC methods, respectively.

Fig. 7
figure 7

Spatial comparison of dry season maximum temperature (°C) of Ensemble RCMs mean for historical period between 1975 and 2005. a Observation, b raw RCMs ensemble mean, c empirical quantile mapping bias-correction method, d parametric quantile mapping bias-correction method, e multi-bias-correction method using N-dimensional probability density function transform, f multi-bias-correction method using Spearman rank correlation dependency, g multi-bias-correction method using Pearson correlation dependency

Full size image

4.5 Cross-sectional assessment of temperature variability

As an example, Fig. 8 shows the latitude-time cross-section of the model ensemble mean temperature variability in the dry season for the entire study period. There is an increase in temperature from lower to higher latitudes for the observation and all BC methods. The uncorrected (raw) model ensemble mean shows the opposite. However, the representation of the magnitude is captured differently by each BC methods. The temperature of ≥ 31 °C is captured from year 1975 to 2015 and 1988 to 2005 between latitudes 10.8°N and 15°N for the observed series (Fig. 8a). The uncorrected model ensemble mean (raw) model, on the other hand, is not able to capture this variability (Fig. 8b). This magnitude is captured between year 2004 and 2005 between latitudes 10.8°N and 13.2°N for EQM (Fig. 8c). The PQM captures this magnitude for all latitudes from year 1998 to 2005. The MBCN and MBCP capture this magnitude between latitudes 11.0°N and 15°N for all the years, although with a temperature of 30 °C in some years. In general, the low temperatures are captured well by the PQM and MBCN methods. However, the high temperatures are mismatched either by the years of occurrence or by the latitudes at which they occurred. The longitudinal cross-section also shows varying degrees of mismatches. However, the PQM seems to perform best (Fig. S10).

Fig. 8
figure 8

Latitude-time cross section of dry season maximum temperature (°C) for the entire study period (1975–2005). a Observation. b Raw and the different BC methods g–f

Full size image

4.6 Trends in temperature

To verify the ability of the different BC methods to correctly replicate the observed trend and trend magnitude of temperature in the study period, the model ensemble mean is subjected to the adopted BC methods at annual, dry and wet periods. As an example, the MBCN method is subsequently used for future trend projection (2020–2050) at RCP 4.5 and 8.5, respectively. The results are presented in the sections below.

4.6.1 Historical trend in temperature

The model ensemble mean boxplots distribution of maximum temperature trend for all stations in the basin between 1975 and 2005 show predominantly positive trends in annual series for the observation, the uncorrected model and all BC outputs (Fig. 9a). None of the methods accurately represents the annual trends, nonetheless, the highest trend range is exhibited by MBCN (0.03–0.13 °C/year) as against the observation with trends ranging between 0.00 and 0.06 °C/year. For the dry season (Fig. 9b), the univariate PQM performed best in estimating the trend with values between 0.02 and 0.09 °C/year. However, for the multivariate BC, the MBCN performed best with values between 0.04 and 1.12 °C/year. There is a constant overestimation of trends for the other multivariate BC methods, while the EQM underestimates the observed maximum trends. For the wet season, no method replicates the observed trend. However, MBCR performed best with values ranging between 0.04 and 1.12 °C/year. Although there are incidences of negative trends in the wet season, no BC method captures this. As noted by Mararun [41], due to the time-independent error component of the climate models (which is arbitrarily time-dependent), the modelled climate change is generally incorrect. This is evident in the trends presented in the uncorrected model—as it constantly shows no definite trend pattern. This invariably affects the BC outputs trend, thereby limiting the efficiency of the BC methods [15].

Fig. 9
figure 9

Boxplots distribution of maximum temperature trend for all stations in the basin between 1975 and 2005. a Annual. b Dry season. c Wet season

Full size image

Furthermore, due to the discrepancies in the performance of the climate models used, the model ensemble mean is used to assess the spatial trend of temperature across the basin for the entire study period (1975–2005). Results show a predominantly positive trend of temperature with the magnitude of trend varying between 0.00 and 0.12 °C/year on the annual scale (Fig. 10). All BC methods overestimate the trends’ magnitude with values between 0.03 and 0.09 °C/year in most parts of the basin. For the dry season (Fig. S15), PQM and MBCN accurately represent the trend with the magnitude of the trend between 0.03 and 0.09 °C/year. However, there are some overestimations in the spatial representation of some parts of the basin. Other multivariate methods overestimate the trends’ magnitude in most parts of the basin. Only MBCR accurately replicates the trend and magnitude of the trend of between 0.02 and 0.1 °C/year of wet season temperature in some parts of the basin (Fig. S16). Other BC methods overestimated the magnitude of the trend by at least 0.04 °C/year.

Fig. 10
figure 10

Spatial comparison of annual maximum temperature trend (positive/negative) and magnitude of trend (°C/year) of Ensemble RCMs mean for historical period between 1975 and 2005. a Observation, b raw RCMs ensemble mean, c empirical quantile mapping bias-correction method, d parametric quantile mapping bias-correction method, e multi-bias-correction method using N-dimensional probability density function transform, f multi-bias-correction method using Spearman rank correlation dependency, g multi-bias-correction method using Pearson correlation dependency

Full size image

4.6.2 Future distribution of maximum temperature and trend

Figure 11a–c shows the spatial distribution of the trend of maximum temperature for the future under RCP 4.5. There is an evident positive trend in annual temperature in the basin with a magnitude between 0.00 and 0.12 °C/year. For the dry season, the trend remains positive with an exception of the area close to the Lake Chad. The magnitude is between − 0.04 and 0.12 °C/year, but the high magnitude of between 0.08 and 0.12 °C/year is seen in the middle part of the basin. For the wet season, a high magnitude of between 0.08 and 0.16 °C/year is dominant in the basin. In comparison with the historical period for all seasons, there is a slight decrease in the magnitude of the trend in the southern part of the basin (from − 0.02 to − 0.04 °C/year), while there is an increasing magnitude (from 0.06 to 0.12 °C/year) in other parts of the basin. However, low magnitudes are present in the south of the basin for every season.

Fig. 11
figure 11

Spatial distribution of maximum temperature trend (positive/negative), magnitude of trend (°C/year) (a–c) and maximum temperature (°C) (d–f) for future period between 2020 and 2050 under RCP 4.5 using MBCN

Full size image

Figure 11d–f shows the spatial distribution of annual, dry season and wet season maximum temperature, respectively, for the future under RCP 4.5. There is an evident 25.00 to 33.70 °C temperature range in the south-western end of the basin. However, the annual temperature ranges from 25.00 to 45.37 °C. This is a significant increase when compared to the historical period (26.00–38.00 °C) (Fig. S8). The dry season temperature ranges between 25.00 and 42.50 °C as against the historical temperature range of 28.70 and 35.50 °C (Fig. 7). For the wet season, the temperature ranges do not differ from the historical period (25.00–36.60 °C). Likewise, the spatial spread of these temperature ranges differs from the historical to the future period.

Under RCP 8.5, the spatial distribution of the trend and magnitude of the trend of maximum temperature between 2020 and 2050 (Fig. 12a–c) show a positive annual trend and the magnitude is between 0.00 and 0.18 °C/year. This is 0.12 and 0.06 °C/year more than the historical period and future period under RCP 45, respectively. The dry season shows a negative trend of between − 0.06 and 0.00 °C/year towards the Sahelian end of the basin, while the other parts of the basin have a magnitude of between 0.00 and 0.18 °C/year. The wet season shows no negative trend but exhibits the highest magnitude of the trend of between 0.00 and 0.24 °C/year. This is 0.14 and 0.08 °C/year more than the historical period and future period under RCP 45, respectively.

Fig. 12
figure 12

Spatial distribution of maximum temperature trend (positive/negative), magnitude of trend (°C/year) (a–c) and maximum temperature (d–f) for future period between 2020 and 2050 under RCP 8.5 using MBCN

Full size image

The spatial distribution of annual maximum temperature (Fig. 12d) shows a temperature range of between 26.00 and 43.15 °C. The dry season temperature (Fig. 12e) ranges from 26.00 to 45.60 °C, while the wet season temperature (Fig. 12f) ranges from 26.00 to 35.80 °C. Whilst there is an increasing temperature for annual and dry season when compared with the historical period and future period under RCP 4.5, the wet season shows a decreasing temperature. For example, the wet season temperature for historical period varies from 25.30 to 36.50 °C; for the future period under RCP 4.5 it varies between 25.00 and 36.60 °C, while for RCP 8.5 it varies between 26.00 and 35.80 °C. While there is an increasing temperature at the south-western part of the basin, the other parts of the basin show relative decreasing temperature.

Even though the uncertainties connected with the use of climate models cannot be under-emphasised for impact studies, this study attempts to reduce the range of uncertainty by using the model ensemble mean as well as other participating individual models.

5 Discussion

In evaluating the different BC methods for maximum temperature distribution correction, MBCN performs best during the dry season for all models, while there are mixed performances between the multivariate BC and the models for the annual and wet periods. Additionally, the performances of these BC methods vary for different climate models. Although the BC methods aim to remove historical biases relative to observation [24], there are still some residual errors which could be attributed to the internal variability of climate models that differ from the observation [41]. As emphasised by Cannon [24], large-scale circulation biases that cannot be adjusted usually limit the efficiency of bias-correction techniques. Also, the multivariate BC methods do not preserve but modify the climate model output temporal sequence (i.e. breaking the temporal consistency) while aiming to restore some properties of the climate model time series. This modification is necessary for correcting the multivariate joint dependency structure [18]. In observing the joint dependency structure between variables, the multivariate BC methods show low RMSE values, indicating the ability of these methods in preserving the joint dependency structure.

In assessing the monthly variability of temperature, the EQM performs well in hot months, whereas PQM and MBCN perform well in replicating the monthly variability. The performance of MBCN agrees with Cannon [23] who reported that MBCN outperforms other multivariate BC techniques for all seasons except in autumn. However, Cannon [23] bias-corrected precipitation and argued that the poorer performance in autumn could be attributed to sampling variability in the calibration sample. In assessing the spatial distribution of temperature variability, there is an increasing annual temperature from the Savanna to the Sahelian part of the basin. This agrees with Funk et al. [42] and Adeyeri et al. [7, 25] who reported separately that the southern edges of the Sahel have the coolest air temperature. Since the BC methods aim to adjust some particular aspects of climate models [41] (e.g. spatial, multivariate, temporal and marginal aspects), it is evident that the climate change signal of the considered aspects is well represented after bias-correction. In the dry season, the multivariate methods overestimate in the Sahelian parts of the basin. However, the coldest part of the basin is accurately replicated. For the wet season, the EQM method overestimates in the Sahelian end of the basin.

For the historical trend and magnitude of trend, there is a positive trend of annual, dry and wet period temperature in most parts of the basin. This could be connected to the warming of the northern Atlantic Ocean and the Mediterranean [25, 43].

However, a small portion of the basin exhibited a varying degree of negative trend in the wet season. In general, the MBCN and MBCR capture these trends relatively well in dry and wet seasons, respectively.

Particularly, the MBCN unlike other multivariate bias-correction algorithms is not limited to specified measure correction of joint dependence (e.g. Spearman rank correlation) neither does it assume stationarity in the temporal sequence of climate models [24]. Nevertheless, it exhibits strong convergence properties using the N-dimensional probability density function transform algorithm [44]. However, the convergence of MBCR and MBCP (based on ranked correlation dependence structure) to the targeted multivariate distribution occurs faster than MBCN.

For the future under RCP 4.5, the positive trend continues for all seasons, however, with increased magnitudes. Conversely, when compared with the historical period, there is a slight decrease in the magnitude of trend in the southern part of the basin, while the northern parts (Sahelian part) have increased magnitude. Under RCP 8.5, the spatial distribution of the trend and magnitude of the trend of maximum temperature shows a more intense annual temperature. These uniformities could be related to the representative concentrated pathway emission scenarios, demonstrating the connection between potential environmental impacts and anthropogenic greenhouse gas emissions. In contrast to the historical temperature and RCP 4.5, the dry season shows a negative trend towards the Sahelian end of the basin. However, the highest magnitude of trend is observed during the wet season. Berg et al. [45] argued that increased temperature in the wet season could be attributed to drying soil processes. On the effect of rising temperature on agriculture and its produce, pastures to feed livestock may be limited, crop yield may reduce drastically and the severity droughts may be intensified [46]. On the other hand, the warming climate will intensify the effects of drought on water demand and supply by natural systems and humans [47]. Additionally, high temperatures could intensify convective precipitation especially in areas like the study area where the ocean plays an important role in driving [25, 45]. This coupled with human activities has modified the basin’s hydrological systems and regimes, thereby affecting the food chain balance, water quality and river’s biodiversity in the basin [25, 26, 40]. Therefore, there is a need for an accurate understanding of the historical climate as well as a correct representation of the future basin’s hydro-climatological features.

6 Conclusion

This study compares multiple bias-correction techniques using eight climate models and their ensemble mean for the historical period (1975–2005) and future (2020–2050) over the KYB for annual, dry and wet periods. The historical period is divided into calibration (1975–1990) and validation (1991–2005) periods. The BC methods adopted are the univariate EQM and PQM as well as the multivariate MBCN, MBCP and MBCR. Mostly, the uncorrected model output performs poorly in replicating the site-specific temperature variability and observed trend over the basin for all seasons. However, the BC model provides a worthy output similar to the observation which buttresses the need for correcting biases in climate models before it can be used for impact studies [48]. Overall, the multivariate methods correct the dependence structure of variables, thereby providing a general-purpose methodology to the climate community. Although the MBC methods correct the inter-variable dependence structure, due to its complex algorithm and iteration sequence, it is time-consuming and computationally expensive. For example, the MBCN is computational more expensive than the other multivariate BC methods, as many iterations are required to converge the distribution to the observed multivariate distribution [24]. In MBCP, bias-correction is done by iteratively correcting the univariate distribution and the inter-variable correlations, until the correlation coefficient between the model and observation is acceptable. Even though the multivariate BC is computationally expensive, it can be used directly in downscaling applications [23] as against critiques on univariate quantile mapping (e.g. Maraun [14]). Furthermore, the energy distance provides concise information on the performance and stability of multimodel-multivariate BC method and is recommended for picking between models and BC algorithms. Beyond these specifics of this present study, more regional climate simulations with improved physical schemes should be adopted to reduce doubts and inconsistencies in model outputs. Additionally, explicit multiple time scales bias correction of climate models should be incorporated. Furthermore, the performances of these BC methods on the basin’s hydrological components should be investigated.