A numerical study for mixed convective peristaltic flow of an Oldroyd-4 constant nanofluid in a planner channel

Abstract

In this paper peristaltic motion of an Oldroyd-4 constant nanofluid under the influence of Buoyancy forces is taken into account. The Buongiorno model is utilized to see the effects of Brownian motion and thermophoresis on the different features of the flow, heat transfer and concentration. In order to facilitate the solution of modeled equations first the governing equations are transformed to system of ordinary differential equations under the assumption of long wavelength and low Reynolds number. The resulting equations are solved using shooting method along with fourth order R. K. method. It is observed that the amplitude of heat flux rises and effective moment of nanoparticles from wall to the center line of the channel which enhance the thermal conductivity at the wall. This is due to the increase in the kinetic energy and Brownian motion. The effects of different parameters are illustrated through graphs and tabulated data is given to compare the effects of shear stress on walls of the channel with Newtonian fluids.

1 Introduction

Peristaltic is mechanism of transportation of physiological fluids. This mechanism is formed in human body like in gastrointestinal system, transport of urine and flow of spermatozoa in reproductive part. The Several authors [1,2,3,4] have studied this mechanism for the better understanding of urine transport from kidney to bladder using Newtonian Constitutive equation. In reality most of the fluid considered in physiology and industrial application are non- Newtonian in nature. Keeping this in mind other researchers discuss the Peristaltic transport phenomena using viscoelastic, rate type, and generalized Newtonian fluid model and Micro polar fluid models [5,6,7,8]. Interaction of heat transfer with peristaltic transport for Newtonian and non-Newtonian fluids have been investigated by many researchers for example Vajravelu et al. [9] study the effect of heat transfer for viscous fluid in an annular. Hayat at el [10] observed the effects of heat transfer in third order fluid with variable viscosity. Das [11] studied the effects of slip and heat transfer of a peristaltic transport of viscous fluid in asymmetric porous channel. Sobh et al. [12] discussed heat transfer in peristaltic flow of viscoelastic fluid in an asymmetric channel. Ahmad et al. [13] highlight the effects of mixed convection on the peristaltic motion of Oldroyd 4-constant fluid in a planner channel. More recently Manjunatha et al. [14] discuss the effects of variable properties on the peristaltic flow of Jeffery fluid in a channel. Ali et al. [15] numerically investigated the influence of heat transfer on the peristaltic flow of Oldroyd 8-constant fluid and heat transfer in a curved channel. In the recent year’s nanofluid dynamics due to its diverse applications in medical and biological sciences, energetic and process system engineering, divert the attention of many researchers. Choi [16] introduced the term nanofluid working with the group at the Argonne National Laboratory (ANL), in 1995. Tripati and Beg [17] used the Buongiorno’s formulation for the Nano fluids which is an application of drug delivery system in the human body. Ebaid et al. [18] studied the nanofluids flow in an asymmetric channel with slip conditions as an application of cancer treatment. Hayat et al. [19] used the convective boundary conditions for the analysis of viscous nanofluid. Narla et al. [20] made the analysis of Jeffery Nano fluid in a curved channel. Kotnurkar and Giddaiah [21] studied the boiconvective flow of Eyring-Powell nanofluid in a porous channel. The applications of magnetic nanoparticles in drug delivery systems transported through peristaltic mechanism has been reported by Rafiq et al. [22]. Recently, a numerical study is performed by Zaman et al. [23] to discuss the influence of nanoparticles for unsteady blood flow in a stenotic artery.Due to complex rheological properties of fluid, many non-Newtonian fluid models take the attention of many researchers. Rate type fluid models are used to describe the response of the fluid that have slight memory. Memory is described as the dependence of the stress on the history of the relative deformation gradient. Maxwell [24] proposed that a body has means for storing energy, which characterize the fluid and a means for dissipating energy which characterizing its viscous nature. The Oldroyd B model is developed by Oldroyd [25] which is characterized by material constants a viscosity, relaxation time and retardation time. The Oldroyd B model is very effective to analyze and also this model has experimental background. When we consider the peristaltic flow under long wavelength approximation there is a lack of viscoelastic properties. In this regard, Oldroyd 4-constant fluid model is taken into account that exhibits viscoelastic properties. The aim of the article is to analyze the Brownian motion and thermophoresis effects on peristaltic flow of Oldroyd- 4 fluids in a planner channel are investigated numerically.

2 Mathematical formulation of the problem and flow configuration

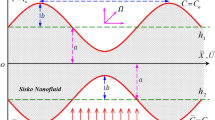
We consider the flow of an incompressible Oldroyd 4-constant nanofluid in a symmetric vertical channel with width $2a$ due to propagation of wave on the wall of the channel. The right wall of the channel maintained at temperature $T_{1}$ and concentration $C_{1}$ and left wall of the channel maintained at temperature $T_{0}$ and concentration $C_{0}$ as in Fig. 1.

Fig. 1

Physical sketch of Problem

The walls surfaces are described by

$$\pm \bar{h}\left( {\bar{X},\bar{t}} \right) = \pm \left( {a + bsin\left[ {\frac{2\pi }{\lambda }\left( {\bar{X} - c\bar{t}} \right)} \right]} \right),$$

(1)

where $b$ is amplitude of the wave $\lambda$ is the wavelength and $\bar{t}$ is the time. The fundamental conservation laws of mass, momentum, energy and nano-particle fraction can be represented by the equations

$$\frac{{\partial \bar{U}}}{{\partial \bar{X}}} + \frac{{\partial \bar{V}}}{{\partial \bar{Y}}} = 0,$$

(2)

$$\rho_{f} \left[ {\frac{{d\bar{U}}}{{d\bar{t}}}} \right] + \frac{{\partial \bar{P}}}{{\partial \bar{X}}} = \frac{{\partial \bar{S}_{{\bar{X}\bar{X}}} }}{{\partial \bar{X}}} + \frac{{\partial \bar{S}_{{\bar{X}\bar{Y}}} }}{{\partial \bar{Y}}} + g\left[ {\left( {1 - C_{0} } \right)\rho_{f} \alpha \left( {\bar{T} - \bar{T}_{0} } \right) + \left( {\rho_{p} - \rho_{{f_{0} }} } \right)\beta \left( {\bar{C} - \bar{C}_{0} } \right)} \right],$$

(3)

$$\rho_{f} \left[ {\frac{{d\bar{V}}}{{d\bar{t}}}} \right] + \frac{{\partial \bar{P}}}{{\partial \bar{Y}}} = \frac{{\partial \bar{S}_{{\bar{X}\bar{Y}}} }}{{\partial \bar{X}}} + \frac{{\partial \bar{S}_{{\bar{Y}\bar{Y}}} }}{{\partial \bar{Y}}},$$

(4)

$$\begin{aligned} & \frac{{d\bar{T}}}{{d\bar{t}}} = \\ & \frac{\kappa }{{\left( {\rho c} \right)_{f} }}\left( {\frac{{\partial^{2} \bar{T}}}{{\partial \bar{X}^{2} }} + \frac{{\partial^{2} \bar{T}}}{{\partial \bar{Y}^{2} }}} \right) + \frac{{\left( {\rho c} \right)_{p} }}{{\left( {\rho c} \right)_{f} }}\left[ {D_{B} \left( {\frac{{\partial \bar{T}}}{{\partial \bar{X}}}.\frac{{\partial \bar{C}}}{{\partial \bar{X}}} + \frac{{\partial \bar{T}}}{{\partial \bar{Y}}}.\frac{{\partial \bar{C}}}{{\partial \bar{Y}}}} \right) + \frac{{D_{T} }}{{T_{m} }}\left( {\left( {\frac{{\partial \bar{T}}}{{\partial \bar{X}}}} \right)^{2} + \left( {\frac{{\partial \bar{T}}}{{\partial \bar{Y}}}} \right)^{2} } \right)} \right] \\ & + \frac{1}{{\left( {\rho c} \right)_{f} }}\left( {\bar{S}_{{\bar{X}\bar{X}}} \frac{{\partial \bar{U}}}{{\partial \bar{X}}} + \bar{S}_{{\bar{X}\bar{Y}}} \left( {\frac{{\partial \bar{U}}}{{\partial \bar{Y}}} + \frac{{\partial \bar{V}}}{{\partial \bar{X}}}} \right) + \bar{S}_{{\bar{Y}\bar{Y}}} \frac{{\partial \bar{V}}}{{\partial \bar{Y}}}} \right), \\ \end{aligned}$$

(5)

$$\frac{{d\bar{C}}}{{d\bar{t}}} = D_{B} \left( {\frac{{\partial^{2} \bar{C}}}{{\partial \bar{X}^{2} }} + \frac{{\partial^{2} \bar{C}}}{{\partial \bar{Y}^{2} }}} \right) + \frac{{D_{T} }}{{T_{m} }}\left( {\frac{{\partial^{2} \bar{T}}}{{\partial \bar{X}^{2} }} + \frac{{\partial^{2} \bar{T}}}{{\partial \bar{Y}^{2} }}} \right),$$

(6)

in the above equations $\rho_{f}$ is the fluid density, $\rho_{p}$ is the nanoparticle mass density, $\bar{U}$ is axial velocity, $\bar{V}$ is transverse velocity, $P$ is pressure, $\mu$ is fluid viscosity, $g$ is gravitational acceleration, $\beta$ is volumetric expansion coefficient of the fluid, $(\rho c)_{f}$ is heat capacity of fluid, $\left( {\rho c} \right)_{p}$ is effective heat capacity of nano-particle, $k$ is thermal conductivity,$D_{B}$ is Brownian diffusion coefficient,$D_{T}$ is thermophoresis diffusion coefficient, $\rho_{{f_{0} }}$ is nano-fluid density at the reference temperature $T_{m}$ and $\bar{S}_{{\bar{X}\bar{X}}} , \bar{S}_{{\bar{X}\bar{Y}}} , \bar{S}_{{\bar{Y}\bar{Y}}}$ are components of extera stress tensor for Oldroyd 4-constant fluid given in [26]. The constitutive equation for Oldroyd 4-constant fluid can be expressed as

$$\bar{S} + \lambda_{1} \frac{{D\bar{S}}}{{D\bar{t}}} + \lambda_{3} tr\left( {\bar{S}} \right)\bar{A}_{1} = \mu \left( {1 + \lambda_{2} \frac{D}{{D\bar{t}}}} \right)\bar{A}_{1} ,$$

(7)

In which $\lambda_{1}$ and $\lambda_{3}$ are relaxation time parameters, $\lambda_{2}$ is the retardation time parameter, $\bar{A}_{1}$ is First Revilian Erisken tensor, $\mu$ is the dynamic viscosity, and $D\bar{S}/D\bar{t}$ is the upper convected time derivative. It is worth to mention that the above model reduces to Oldroyd B model if $\lambda_{3} = 0$ and a verity of rheological properties can be described by this model and more accurate results can be obtain for the viscoelasticity and this model is used by many researchers [27,28,29] to discussed the peristaltic motion of viscoelastic fluid in different geometries under different conditions. When the peristaltic motion of viscoelastic fluid is describe using Oldroyd B model under the long wave length approximations the retardation time parameter vanished and this deficiency can be overcome using a larger class of viscoelastic fluid which is given in the above expression and using this model peristaltic motion has been discussed by [8, 30]. As in the Laboratory frame $\left( {\bar{X},\bar{Y}} \right)$ the flow in the channel is unsteady. But, it can be treated as steady in the coordinate frame $\left( {x,y} \right)$ moving with the wave speed c (Wave frame). So we can relate the coordinates and velocities in the two frames as $x = \bar{X} - ct, y = \bar{Y} u = \bar{U} - c, v = \bar{V}$ and $\bar{P}\left( {\bar{X},\bar{Y}} \right) = p\left( {x,y} \right),$ where $u$ and $v$ are velocity components in the wave frame.

Then above equations reduces to

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$

(8)

$$\rho_{f} \left[ {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right] + \frac{\partial p}{\partial x} = \frac{{\partial S_{xx} }}{\partial x} + \frac{{\partial S_{xy} }}{\partial y} + g\left[ {\left( {1 - C_{0} } \right)\rho_{f0} \alpha \left( {T - T_{0} } \right) + \left( {\rho_{p} - \rho_{f0} } \right)\beta \left( {C - C_{0} } \right)} \right],$$

(9)

$$\rho \left[ {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right] + \frac{\partial p}{\partial y} = \frac{{\partial S_{xy} }}{\partial x} + \frac{{\partial S_{yy} }}{\partial y},$$

(10)

$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{\kappa }{{\left( {\rho c} \right)_{f} }}\left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) + \tau \left[ {D_{B} \left( {\frac{\partial T}{\partial x}.\frac{\partial C}{\partial x} + \frac{\partial T}{\partial y}.\frac{\partial C}{\partial y}} \right) + \frac{{D_{T} }}{{T_{m} }}\left( {\left( {\frac{\partial T}{\partial x}} \right)^{2} + \left( {\frac{\partial T}{\partial y}} \right)^{2} } \right)} \right] + \frac{1}{{\left( {\rho c} \right)_{f} }}\left( {S_{xx} \frac{\partial u}{\partial x} + S_{xy} \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right) + S_{yy} \frac{\partial v}{\partial y}} \right),$$

(11)

$$u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{B} \left( {\frac{{\partial^{2} C}}{{\partial x^{2} }} + \frac{{\partial^{2} C}}{{\partial y^{2} }}} \right) + \frac{{D_{T} }}{{T_{m} }}\left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) .$$

(12)

Introducing the variables and the stream functions

$$\left. {\begin{array}{*{20}c} {x^{*} = \frac{2\pi x}{\lambda }, y^{*} = \frac{y}{a}, u^{*} = \frac{u}{c}, v^{*} = \frac{v}{c},\bar{h} = \frac{h}{a}, p^{*} = \left( {\frac{{2\pi a^{2} }}{\lambda \mu c}} \right)p, S^{*} = \left( {\frac{a}{\mu c}} \right)S,\lambda_{1}^{*} = \frac{a}{c}\lambda_{1} ,} \\ { \lambda_{2}^{*} = \frac{a}{c}\lambda_{2} , \lambda_{3}^{*} = \frac{a}{c}\lambda_{3} ,\delta = \frac{2\pi a}{\lambda }, u = \frac{\partial \psi }{\partial y}, v = - \delta \frac{\partial \psi }{\partial x}, \theta = \frac{{T - T_{0} }}{{T_{1} - T_{0} }}, \zeta = \frac{{C - C_{0} }}{{C_{1} - C_{0} }},Re = \frac{\rho ca}{\mu }} \\ \end{array} } \right\}$$

(13)

Equation (8) is identically satisfied and (9) to (12) after using $\delta \ll 1$ and low Reynolds approximation and after dropping the * takes the form

$$\frac{\partial p}{\partial x} = \frac{{\partial S_{xy} }}{\partial y} + \left[ {G_{r} \theta + Gc\zeta } \right],$$

(14)

$$\frac{\partial p}{\partial y} = 0,$$

(15)

$$\left( {\frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right) + PrNb\left( {\frac{\partial \theta }{\partial y}.\frac{\partial \zeta }{\partial y}} \right) + PrNt\left( {\left( {\frac{\partial \theta }{\partial y}} \right)^{2} } \right) + Br\left( {S_{xy} \left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)} \right) = 0,$$

(16)

$$\left( {\frac{{\partial^{2} \zeta }}{{\partial y^{2} }}} \right) + \frac{Nt}{Nb}\left( {\frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right) = 0,$$

(17)

where

$$Pr = \frac{{\mu c_{f} }}{ \kappa }, Nb = \tau D_{B} \frac{{(C_{1} - C_{0} )}}{\nu },Nt = \tau \frac{{D_{T} }}{{T_{m} }}\frac{{\left( {T_{1} - T_{0} } \right)}}{\nu },Ec = \frac{{c^{2} }}{{\left( {c_{f} } \right) \left( {T_{1} - T_{0} } \right)}},Gr = \frac{{\left( {1 - C_{0} } \right)\left( {T_{1} - T_{0} } \right)g\alpha a^{2} }}{c \nu },$$

$$Gc = \frac{{\left( {\rho_{p} - \rho_{f0} } \right)g\beta \left( {C_{1} - C_{0} } \right)}}{c \mu }, \;{\text{and}}\;S_{xy} = \frac{{1 + 2\alpha_{1} \left( {\frac{{\partial^{2}\uppsi}}{{\partial y^{2} }}} \right)^{2} }}{{1 + 2\alpha_{2} \left( {\frac{{\partial^{2}\uppsi}}{{\partial y^{2} }}} \right)^{2} }}\left( {\frac{{\partial^{2}\uppsi}}{{\partial y^{2} }}} \right), \alpha_{1} = \lambda_{2} \lambda_{3} , \alpha_{2} = \lambda_{1} \lambda_{3} .$$

The appropriate boundary conditions which satisfied by velocity, temperature and nano concentration profile in dimensionless form are

$\psi = \mp \frac{F}{2}, \frac{d\psi }{dy} = - 1, \theta = \left\{ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right\},\zeta = \left\{ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right\}.$ at $\pm y = \pm 1 \pm \phi Sin\left( x \right)$ where $\phi$ is amplitude ratio.

3 Solution procedure

Analytical solution of Eqs. (14)–(17) is difficult due to their strong coupling and nonlinearity so to facilitate their solution we use shooting method. For this

Reducing Eq. (14)–(17) into first order equations

Let $\psi = y_{1} , \theta = y_{5} \,\,and\,\, \zeta = y_{7} .$

$$y_{1}^{'} = y_{2,}$$

(18)

$$y_{2}^{'} = y_{3} ,$$

(19)

$$y_{3}^{'} = y_{4} ,$$

(20)

$$\begin{aligned} y_{4}^{{\prime }} & = \frac{{ - 12y_{3} y_{4}^{2} \alpha_{1} + 12y_{3} y_{4}^{2} \alpha_{2} + 8y_{3}^{3} y_{4}^{2} \alpha_{1} \alpha_{2} - 8y_{3}^{3} y_{4}^{2} \alpha_{2}^{2} }}{{\left( {1 + 2y_{3}^{2} \alpha_{2} } \right)\left( {1 + 6y_{3}^{2} \alpha_{1} - 2y_{3}^{2} \alpha_{2} + 4y_{3}^{4} \alpha_{1} \alpha_{2} } \right)}} \\ & \quad + \,\frac{{Gr\left( { - y_{6} - 6y_{3}^{2} y_{6} \alpha_{2} - 12y_{3}^{4} y_{6} \alpha_{2}^{2} - 8y_{3}^{6} y_{6} \alpha_{2}^{3} } \right)}}{{\left( {1 + 2y3^{2} \alpha_{2} } \right)\left( {1 + 6y3^{2} \alpha_{1} - 2y3^{2} \alpha_{2} + 4y3^{4} \alpha_{1} \alpha_{2} } \right)}} \\ & \quad + \,\frac{{Gc\left( {y_{8} + 6y_{3}^{2} y_{8} \alpha_{2} + 12y_{3}^{4} y_{8} \alpha_{2}^{2} + 8y_{3}^{6} y_{8} \alpha_{2}^{3} } \right)}}{{\left( {1 + 2y_{3}^{2} \alpha_{2} } \right)\left( {1 + 6y_{3}^{2} \alpha_{1} - 2y_{3}^{2} \alpha_{2} + 4y_{3}^{4} \alpha_{1} \alpha_{2} } \right)}}, \\ \end{aligned}$$

(21)

$$y_{5}^{'} = y_{6} ,$$

(22)

$$y_{6}^{'} = \frac{{ - Bry_{3}^{2} - NtPry_{6}^{2} - NbPry_{6} y_{8} - 2Bry_{3}^{4} \alpha_{1} - 2NtPry_{3}^{2} y_{6}^{2} \alpha_{2} - 2NbPry_{3}^{2} y_{6} y_{8} \alpha_{2} }}{{1 + 2y3^{2} \alpha_{2} }},$$

(23)

$$y_{7}^{'} = y_{8} ,$$

(24)

$$y_{8}^{'} = \frac{{NtPry_{6} \left( {Nty_{6} + Nby_{8} } \right) + \frac{{BrNty_{3}^{2} \left( {1 + 2y_{3}^{2} \alpha_{1} } \right)}}{{1 + 2y_{3}^{2} \alpha_{2} }}}}{Nb}.$$

(25)

Subject to the initial conditions

$$y_{1} \left( { - y} \right) = \frac{F}{2}, y_{1}^{'} \left( { - y} \right) = - 1,y_{2} '\left( { - y} \right) = p,y_{3} '\left( { - y} \right) = q,y_{5} \left( { - y} \right) = 0,$$

$$y_{6} \left( { - y} \right) = r,y_{7} \left( { - y} \right) = 0, y_{8} \left( { - y} \right) = s.$$

We integrate system of initial value problems from $\left( {18 - 25} \right)$ using 4th order RK-methods. Where $p,q,r$ and $s$ are missing slopes which are updated by Newton’s method.

In graphical illustration of pressure rise per wavelength and heat flux at the upper wall of the channel following relations are used.(reference related papers)

$$\Delta p_{\lambda } = \mathop \int \limits_{0}^{1} \frac{dp}{dx}dx,$$

(26)

$$Z = \frac{\partial h}{\partial x}\left. {\frac{\partial \theta }{\partial y}} \right|_{y = h} .$$

(27)

4 Graphical results and discussions

In this section we investigated the effects of interesting parameters on the various features of the peristaltic motion.

The Fig. 2 illustrate the effects of thermal buoyancy parameter ($Gr$) and nanoparticle fraction buoyancy parameter ($Gc$) on the axial velocity profile. It is observed that by increasing both $Gr$ and $Gc$ the axial velocity profile increases in the left half of the channel and shows the converse relation in the right half of the channel. In the absence of thermal buoyancy force parameter and nanoparticle fraction buoyancy parameter the axial velocity is symmetric about the central line of the channel and by increasing these parameters this symmetry is disturbed due to the domination of buoyant forces over the viscous forces due to the variation in the temperature and concentration of the nanoparticles.

Fig. 2

(a):- Effects of $Gr$ on $u \left( y \right)$ when $Gc$ = 0.1 (b):- Effects of $Gc$ on $u \left( y \right)$ when $Gr = 0.1$. Other parameters are $\phi = 0.3,F = - 0.8,\alpha_{1} = 0.5,\alpha_{2} = 2,Br = 0.1,Pr = 1,Nt = 0.1 \,{\text{and }}\,Nb = 0.5$

Effects of thermal buoyancy parameter ($Gr$) and nanoparticle fraction buoyancy parameter (Gc) on are represented in Fig. 3 The temperature profile increases for the increasing values of the $Gr$ and $Gc$. The effects of $Gr$ and $Gc$ on temperature profile are maximum at the central line of the channel and reduces at the walls of the channel, this is due to the fact that the disturbance at the walls of the channel is minimum and the gravity is dominant at the central line of the channel.

Fig. 3

(a):- Effects of $Gr$ on $\theta \left( y \right)$ when $Gc = 0.1$ Fig. 3(b):- Effects of $Gc$ on $\theta \left( y \right)$ when $Gr = 0.1$. Other parameters are $\phi = 0.3,F = - 0.8,\alpha_{1} = 0.5,\alpha_{2} = 2,Br = 2.5,Pr = 1,Nt = 0.1\, {\text{and }}\,Nb = 0.5$

Figure 4 shows the effects of Thermal buoyancy parameter $\left( {Gr} \right)$ and nanoparticles fraction buoyancy parameter $\left( {Gc} \right)$ on the nanoparticles fraction profile. It is observed that nanoparticles fraction profile shows a decreasing behaviour for the increasing values of buoyancy parameters.

Fig. 4

(a):- Effects of $Gr$ on $\zeta \left( y \right)$ when $Gc = 0.5$ Fig. 4(b):- Effects of $Gc$ on $\zeta \left( y \right)$ when $Gr = 0.5.$ Other parameters are $\phi = 0.3,F = - 0.8,\alpha_{1} = 0.5,\alpha_{2} = 2,Br = 2.5,Pr = 1,Nt = 0.5\, {\text{and }}\,Nb = 1.0$

Effects of rheological parameters of the fluid on the nanoparticle fraction profile are demonstrated in the Fig. 5. Figure 5a is for the increasing values of the $\alpha_{1}$, up to 0.5 which shows that concentration profile decreases and Fig. 5b is for the increasing values of $\alpha_{2}$, with $\alpha_{1} = 0.5$ the nanoparticle fraction profile increases and in both Fig the curve for $\upalpha_{1} = 0.5 =\upalpha_{2}$ shows the Newtonian behavior.

Fig. 5

(a):- Effect of $\alpha_{1}$ on $\zeta \left( y \right)$ when $\alpha_{2} = 0.5$ (b):- Effect of $\alpha_{2}$ on $\zeta \left( y \right)$ when $\alpha_{1} = 0.5$ Other parameters are $\phi = 0.3,F = - 0.8, Br = 1.5,Pr = 1, Nt = 0.1,Nb = 0.5,Gc = 0.3\, {\text{and}}\, Gr = 0.5$

The effects of prandtle number ($Pr$) and ($Br$) on nanoparticles fraction profile are shown in Fig. 6 which represents that nanoparticle fraction profile decreases for increasing values of Prandtl and Brinkman number for viscous dissipation effects.$Br = 0.0$ is for no viscous dissipation and the curve is not linear due to the non-Newtonian behavior of the fluid. The nanoparticle concentration distribution decreases with increasing both Prandtl number and Brinkman number. As Prandtl number $Pr$ is ratio of viscous forces to the thermal forces the concentration decreases due to domination of viscous force over the thermal forces in the nanofluid. Also due to the increase in the viscous dissipation the enthalpy decreases which cause a remarkable decrease in the nanoparticle concentration profile.

Fig. 6

(a):- Effect of $Pr$ on $\zeta \left( y \right)$ when $Br = 1.5$ (b):- Effect of $Br$ on $\zeta \left( y \right)$ when $Pr = 1.0$ Other parameters are $\phi = 0.3,F = - 0.8,\alpha_{2} = 0.5,\alpha_{2} = 2,Nt = 0.1,Nb = 0.5,Gc = 0.3\, and\, Gr = 0.5$

In Fig. 7 the effects of thermophoretic parameter ($Nt$) and Brownian motion parameter ($Nb$) on temperature profile are represented. It is seen from Fig. 7a that as we increase the thermopherises parameter (Nt) the temperature profile increases. This increase is due to the effective movement of nanoparticles from the walls to the central line of the channel because due to the collusion of nanoparticles increases the internal kinetic energy of the particles which enhance the thermal conductivity of the base fluid. The microscopic structure of the nanoparticles in the fluid and inter particle forces results in the increase in micro convection of the base fluid which enhance the heat transfer. Due to this reason the temperature profile also shows increasing behavior for the increasing values of (Nb).

Fig. 7

a Effects of $Nt$ on $\theta \left( y \right)$ when $Nb = 0.5$. b Effects of $Nb$ on $\theta \left( y \right)$ when $Nt = 0.1$. Other parameters are $\phi = 0.3,F = - 0.8, Pr = 1,\alpha_{1} = 0.5,\alpha_{2} = 2,Br = 0.5, Gc = 0.3\, and\, Gr = 0.5$

The effects of thermopherises parameter ($Nt$) and Browanian motion parameter ($Nb$) are presented in Fig. 8. The nanoparticles fraction profile shows a remarkable decrease for the increasing values $Nt$. As due to internal fraction between the nanoparticles the rate of transfer of nanoparticles in the channel becomes smaller this results a remarkable decrease in the nanoparticles fraction profile and a small increase is observed for the increasing values of the $Nb$.

Fig. 8

a Effects of $Nt$ on $\zeta \left( y \right)$ when $Nb = 0.5$. b Effects of $Nb$ on $\zeta \left( y \right)$ when $Nt = 0.1$ Other parameters are $\phi = 0.3,F = - 0.8,Pr = 1,\alpha_{1} = 0.5,\alpha_{2} = 2Br = 1,Gc = 0.3\, and\, Gr = 0.5$

Effects of thermopherises parameter (Nt) and Brownian motion parameter (Nb) on the heat transfer coefficient Z on the right wall of the channel is plotted in Fig. 9. The amplitude of heat flux increases for the increasing values of the Nt and Nb.

Fig. 9

a Effects of $Nt$ on Z when $Nb = 0.5$. b Effects of $Nb$ on Z when $Nt = 0.1$ Other parameters are $\phi = 0.3,F = - 0.8,Pr = 0.5,\alpha_{1} = 0.5,\alpha_{2} = 2,Br = 0.5,Gc = 0.5\, and\, Gr = 0.5$

The influence of both Buoyancy parameters for temperature ($Gr$) and nanoparticles particle fraction profile ($Gc$) are exhibited in Fig. 10. The amplitude heat transfer coefficient Z also show increasing trend for the increasing values of $Gr$ and $Gc$. These effects are obviously dominant due to the increase buoyancy forces.

Fig. 10

a Effects of $Gr$ on Z when $Gc = 0.5$. b Effects of $Gc$ on Z when $Gr = 0.5$. Other parameters are $\phi = 0.3,F = - 0.8,Pr = 0.5,\alpha_{1} = 0.5,\alpha_{2} = 2,Br = 0.5,Nt = 0.1\, and\, Nb = 0.5$

The behavior of stream lines for different values of $Gr$ and $Gc$ are shown in Figs. 11 and 12. As we increase the Thermal Buoyancy parameter the size of the bolus increases in left half of the channel and it can be seen easily that the disturbance is shifted from left to the right half of the channel. The similar behavior can be seen for the increasing values of nanoparticle fraction Buoyancy parameter in Fig. 12.

Fig. 11

Stream lines for a Gr = 0 b Gr = 0.5 and c Gr =1.0. Other Parameters are $\phi = 0.6,F = - 0.2,Pr = 0.7,\alpha_{1} = 0.5,\alpha_{2} = 2,Br = 1,Nt = 0.1,Gc = 0.1\, and\, Nb = 0.5$

Fig. 12

Stream lines for a Gc = 0 b Gc = 0.5 and c Gc =1.0. Other Parameters are $\phi = 0.6,F = - 0.2,Pr = 0.7,\alpha_{1} = 0.5,\alpha_{2} = 2,Br = 1,Nt = 0.1,Gr = 0.1\, and\, Nb = 0.5$

It can be seen that from Fig. 13a the pressure rise per wavelength shows a remarkable decrease for the increasing values of thermal buoyancy parameter Gr. Similar trend can be observed for the increasing values of nanoparticles fraction parameter $Gc$. From these one can conclude that fluid transport is strongly affected by both thermal and nanoparticles fraction buoyancy parameters. The increase in thermopherises parameter $\left( {Nt} \right)$ causes a significant increase in the pressure difference and similar behavior is observed for the increasing values of Brownian motion parameter $\left( {Nb} \right)$ which means that both Thermopherises and Brownian motion assist the flow. As the pressure gradient is directly proportional to the kinetic energy of the nanoparticles so for the increasing values of both Brownian motion and thermophoresis parameters the kinetic energy increases as a result the pressure drop per wavelength increases in all regions (Fig. 14).

Fig. 13

a Effect of $Gr$ on pressure rise per wavelength when $Gc = 0.1$. b Effect of $Gc$ on pressure rise per wavelength when $Gr = 0.1.$. Other parameters are $\phi = 0.3, Pr = 0.7,\alpha_{1} = 0.5,\alpha_{2} = 2,Br = 0.1,Nt = 0.1\, and\, Nb = 0.5$

Fig. 14

a Effect of $Nt$ on pressure rise per wavelength when $Nb = 0.5$. b Effect of $Nb$ on pressure rise per wavelength when $Nt = 0.1$. Other parameters are $\phi = 0.3, Pr = 1,\alpha_{1} = 0.5,\alpha_{2} = 2,Br = 2,Gr = 1\, and\, Gc = 1$

The numerical values of shear stress at both left and right walls of the channel are presented in Table 1. It is evident from the tabulated data the shear stress decreases with increasing both thermal and density Grashof numbers at the left wall of the channel while show opposite trend on the right wall of the channel. Furthermore the magnitude of shear stress is increasing function of both thermal and density Grashof number for the Newtonian case. The results are similar for the non-Newtonian case (i.e. $\alpha_{1} = 0.5, \alpha_{2} = 2.0)$ also the magnitude of shear stress decreases as we move from Newtonian to non-Newtonian case. The magnitude of shear stress at the left wall increases but at the right wall decreases with increasing the Prandtl number for Newtonian case while for non-Newtonian case shear stress decreases at the both walls this is due to domination of viscous effects. Furthermore the shear stress is a decreasing function of Brinkman number because of the internal kinetic energy.

Table 1 Shear stress at the Left and right walls of the channel

The stress increases with increasing viscous dissipation and for Newtonian case its magnitude is large as compared to the non-Newtonian. The shear stress decreases at both the walls due to the increase in the Brownian motion which cause the loss in the internal energy. Due to the increase in the thermopheratic effects the shear stress increases at both the walls of the channel.

5 Conclusions

A numerical study for an Oldroyd 4-Constant nanofluid is taken into account in this paper. Effects of thermal and nanoparticles fraction buoyancy forces on the different features are also considered.

The axial velocity and temperature profile increases while nanoparticle fraction profile by increasing the thermal and nanoparticle fraction buoyancy forces.

The Rheological parameters of the fluid $\alpha_{1}$ and $\alpha_{2}$ have opposite effects on the nanoparticle fraction profile.

Temperature profile in an increasing function of both $Nt$ and Nb.

The heat transfer coefficient shows oscillatory behavior and its magnitude increases by increasing $Nt$ and $Nb$.

The size of the trapping bolus increases in left half of the channel by increasing $Gr$ and $Gc$.

Pressure rise per wavelength increases in all regions with increasing Brownian motion and thermopherises parameter.