1 Introduction

To obtain stability through the gyroscopic effect, overcome the adverse interference caused by thrust eccentricity, mass eccentricity, and aerodynamic eccentricity, or simplify the control system, many projectiles fly while spinning around its longitudinal axis. When the rotational angular velocity of a spinning missile does not coincide with the flight velocity, side force and moment will be generated, which is called the Magnus effect [1]. Although the Magnus force and Magnus moment are small in magnitude, they have a great impact on the stability of the projectile. The coning motion induced by the side force and yawing moments can result in flight failure. The American Tomahawk sounding rocket flight failed approximately 20 times due to the divergence of coning motion [2]. Thus, accurate prediction of the Magnus effect and in-depth study of its generation mechanism are the long-term goals of researchers.

There have been many studies on the Magnus effect of slender bodies [3,4,5,6,7,8]. The distorted boundary layer due to spinning is the main reason for the Magnus effect of the spinning body. For the body-fin configuration, the side force and yawing moment have obvious unsteady characteristics over time, the flow mechanism is more complicated than the Magnus effect of the slender body, and relative research is limited. The additional angle of attack, additional velocity difference of the fins, and the impact of the shedding vortices on the fins will have extra effects [9,10,11]. The canard-body-fin configuration is more complex. The flow around the canard root causes continuous disturbance to the projectile body, separation vortices, and leeward fins [12].

Theoretical and experimental methods were used to study the Magnus effect of complicated configurations in early times. Nietubicz and Opalka [13] and Jenke [14] performed wind-tunnel experiments on missiles with different configurations to study the influence of spin rate on the Magnus effect. The results show that the side force and yawing moment varied linearly with the spin rate. Benton [15, 16] proposed the calculation formula of the Magnus moment derivative, which was in good agreement with the experiment at high Mach. Platou [17] found that when there was an angle of attack, the aerodynamic loads of the leeward fin and windward fin were different, resulting in the direction of the fin side force being opposite to the body side force. Seginer and Rosenwasser [18] found the phenomenon of side force reversal in wind-tunnel experiments. Eastman [19] and Su et al. [20] performed wind-tunnel experiments on spinning missiles controlled by canards. However, the interference effect between the various pneumatic components was not studied in detail by theories and wind-tunnel experiments.

With the development of calculation methods and technologies, computational fluid dynamics (CFD) methods have been increasingly used to simulate complex flow fields. Numerical simulations were carried out to study the Magnus effect of complicated configurations. Pechier et al. [21] studied the Magnus effect of the body-fin configuration at small angles of attack (\(\alpha < 4.2^\circ\)) in supersonic flows. The results show that the direction of the Magnus force of the fin and the body is opposite, and the Magnus force of the fin is dominant. Bhagwandin [9] carried out numerical simulations of the total aerodynamic coefficients and dynamic derivatives of the body-fin configuration under supersonic conditions within the angles of attack range from 0° to 90°. Yin et al. [11] used the \(\gamma - {\text{Re}}_{\theta t}\) transition model to simulate the aerodynamic characteristics of the spinning AFF configuration, revealing the interference mechanism of the projectile body and the fin. Research on spinning canard-body-fin configurations is also limited. Nygaard and Meakin [22] used structured overlapping grids to study the aerodynamic characteristics of the above model and considered the motion of the canard rudder. The results showed that the viscous effect played an important role in the simulation to obtain the interaction between the canard vortex and the body boundary layer. Wang et al. [23] studied the aerodynamic characteristics of a rotating tail rudder using the shear stress transport k-ω model. The results showed that the average control force of the tail rudder is not zero, and it increases with increasing angle of attack, Mach number, and tail rudder spin rates. Sheng et al. [12] used unstructured overlapping grids to study the configuration with canard at M = 0.8–2.2, \(\alpha = 0^\circ \sim 15^\circ\). The results show that with the increase of angles of attack at supersonic speed, for the spinning projectile with fixed canards, the flow around the root would cause continuous interference to the flow near the projectile.

In the above works, the analysis of the flow mechanism of the canard was not deep enough, the body slenderness ratio was small, and the fins had no installation angle. Therefore, research on the Magnus effect still has strong limitations. In this study, the \(\gamma - {\text{Re}}_{\theta t}\) transition model was used to systematically study the aerodynamic performance and flow structures of the spinning finned configuration when freestream is supersonic. First, the aerodynamic performance and flow mechanisms of the body and the fins were obtained through slender body, body-fin configuration, and canard-body-fin configuration. Second, the effect of the body slenderness ratio was revealed. Third, the influence of the fin installation angle on the body and itself is investigated.

2 Numerical Approach

2.1 Numerical Methods

3D unsteady Reynolds-time-averaged Navier–Stokes (RANS) modeling is used for simulations of the spinning projectile flow field. A finite volume method is used to solve the RANS equations. The governing equations are:

$$ \frac{\partial }{\partial t} = \iiint_{V} {\mathbf{W}}{\text{d}}V + \iint_{\partial V} {[{\mathbf{F}} - {\mathbf{G}}]} \cdot \vec{n}{\text{d}}S = \iiint_{V} {\mathbf{H}}{\text{d}}V, $$
(1)

where W is convective terms, F and G are the inviscid and viscious flux vectors, H is the source terms, and V represents the cell volume.

$$ \begin{aligned} {\mathbf{W}}& = \left[ \begin{gathered} \rho \\ \rho u_{i} \\ e \\ \end{gathered} \right],\;\;{\mathbf{F}} = \left[ \begin{gathered} \rho \left( {\vec{V} - \vec{V}_{{{\text{grid}}}} } \right) \\ \rho u_{i} \left( {\vec{V} - \vec{V}_{{{\text{grid}}}} } \right) + PI \\ e\left( {\vec{V} - \vec{V}_{{{\text{grid}}}} } \right) + P\vec{V} \\ \end{gathered} \right],\\ {\mathbf{G}} &= \left[ \begin{gathered} 0 \\ \sigma_{ij} n_{i} \\ \left( {u_{j} \sigma_{ij} - q_{i} } \right)n_{i} \\ \end{gathered} \right],\end{aligned} $$
(2)

where the grid motion is considered. For the Reynolds averaging treatment of the N–S equation, the above physical quantities have the following forms:

$$ \sigma_{ij} = \left( {\mu + \mu_{t} } \right)\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right) - \frac{2}{3}\left( {\mu + \mu_{t} } \right)\frac{{\partial u_{k} }}{{\partial x_{k} }}\sigma_{ij} , $$
(3)
$$ q_{i} = \frac{1}{\gamma - 1}\left( {\frac{\mu }{\Pr } + \frac{{\mu_{t} }}{{\Pr_{t} }}} \right)\frac{\partial T}{{\partial x_{i} }}, $$
(4)

where \(\gamma\) = 1.4 for ideal gas. \(\mu_{{\text{t}}}\) is the turbulence viscosity coefficient and can be obtained by solving the turbulence model. \({\text{Pr}}\) and \({\text{Pr}}_{{\text{t}}}\) are Prandtl numbers for laminar flow and turbulent flow.

$$ e = \frac{P}{\gamma - 1} + \frac{{\left( {u^{2} + v^{2} + w^{2} } \right)}}{2}, $$
(5)
$$ P = \rho RT, $$
(6)

where R = 287 J/(kg K). The implicit dual-time stepping method was used [24, 25]. The \(\gamma - {\text{Re}}_{\theta t}\) transition model [26, 27] was used to solve the entire flow field. The focus of this study is to investigate the effects of flow mechanisms other than transition on the side force and yaw moment characteristics of spinning missiles. The transition model was used to simulate a more realistic flow structure, and the analysis did not compare the differences among laminar, turbulent, and transition. More work on transition models can be found in references [28, 29].

2.2 Mesh Generation and Boundary Conditions

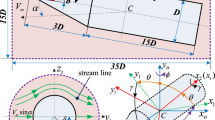
The AFF and the Apache projectile with a large slenderness ratio, as shown in Fig. 1, were selected for study. For the AFF configuration, the body diameter is d = 45.72 mm, and the slenderness ratio is L/d = 10. Four fins are symmetrically distributed without installation angles. A set of uncanted canard was added to the front of the projectile for comparison. For the Apache configuration, the body diameter is d = 58.7 mm, and the slenderness ratio is L/d = 24.88. The installation angle of the fin is 2° (backward-looking counterclockwise differential), and the configuration without a fin installation angle was selected for comparison. The calculation conditions used are shown in Table 1, and the aerodynamic moment reference length is the projectile diameter. \( \overline{X}_{{{\text{cg}}}}\) is the nondimensional mass center of the projectile and the aerodynamic moment reference point. \(\Delta T\) is the physical time step and \(\Delta T = 2\pi /\omega_{x} N\).

Fig. 1
figure 1

Schematic of the AFF and Apache: a AFF, bApache

Full size image
Table 1 Simulation parameters
Full size table

Figure 2 shows the structured mesh for simulations. To study the source of the Magnus effect of the whole projectile, the contribution of each aerodynamic component and aerodynamic interference between different components are analyzed. Three slender bodies with different slenderness ratios are used for numerical simulations in Sect. 4.1.2 to study the slenderness ratio on the side force of the body. Three finned Apache configurations with different slenderness ratios and a single fin are used for numerical simulations in Sect. 4.2.1 to study the effect of the slenderness ratio on the side force of the fin. Therefore, ten calculation models are used. For AFF configurations, the slender body is defined as configuration A, the body-fin configuration is defined as configuration B, and the canard-body-fin configuration is defined as configuration C.

Fig. 2
figure 2

Computational grids for AFF and Apache: a AFF body-fin configuration, b AFF slender body, c AFF canard-body-fin configuration, d Apache with x/d = 24.88, e Apache with x/d = 20, f Apache with x/d = 15, g Apache slender body, h Apache single fin

Full size image

To capture the flow in the boundary layer accurately, the boundary spacing was selected to ensure a nondimensional wall distance \(y^{ + } \le 1\). Thus, the height of the first layer grid was set to \(\Delta h = 5 \times 10^{ - 6} {\text{m}}\) for AFF and \(\Delta h = 2 \times 10^{ - 6} {\text{m}}\) for Apache. The far field was located 20 times the missile diameter (20 d) ahead of the missile nose since the external flow was supersonic. The outlet boundary was located 10 d behind the base. The direction of the spin was clockwise when viewed from the missile head. The mesh details for the two projectiles are shown in Table 2. It should be noted that the points in the three directions given in Table 2 are the axial direction of the projectile body, the spanwise direction of the fin, and the circumferential direction of the projectile. At the initial time of calculation, the fins were “ + ” type, and four fins were evenly distributed along the circumferential direction of the projectile. The force of each fin was similar when spinning, so only the + y side fin (leeward of the projectile) at the initial time was selected for specific analysis in this study.

Table 2 Grid parameters
Full size table

3 Validation of Numerical Methods

The experimental data [14] were used to compare and verify the numerical results of AFF. Figure 3 shows that the variation trends of the side force and yawing moment coefficients with the angle of attack are in good agreement with the experimental results.

Fig. 3
figure 3

Time-averaged aerodynamic coefficients versus angle of attack of AFF: a side force coefficient, b yawing moment coefficient

Full size image

The experimental data [30] were used to compare and verify the numerical results of Apache. The variation in the time-averaged side force coefficient and yawing moment coefficient of spinning Apache with angles of attack when M = 3.0 and \(\overline{\omega } = 0.011\) is shown in Fig. 4. When \(\alpha \le 8^\circ\), the calculated results are in good agreement with the experimental values, and the relative difference is kept within 15%. When α = 12°, the relative difference between the numerical results and the experimental data is close to 30%. The reason may be that when the slenderness ratio is large and the axial flow structure is complex, the current method has limitations in capturing boundary layer transition, flow separation, and vortex dissipation. It should be noted that the side force and yaw moment coefficient have strong nonlinear characteristics with the change of angles of attack. When the angle of attack increases from 8.0° to 12.0°, the side force coefficient decreases significantly, and the yaw moment coefficient changes from negative to positive. The results above had good agreement with the experiments and verified the reliability of the numerical method.

Fig. 4
figure 4

Time-averaged aerodynamic coefficients versus angle of attack of Apache: a side force coefficient, b yawing moment coefficient

Full size image

4 Results and Discussion

4.1 Variation and Origin of Body Side Force

4.1.1 Interference of Uncanted Fin and Canard on the Body

The objects of this section are the AFF with three different configurations. Figure 5 shows the distributed side force coefficient of the projectile body at different angles of attack when M = 2.5, \(\overline{\omega } = 0.025\). The time-averaged side force coefficients of configuration A and body part of configuration B are basically the same, indicating that the fin without installation angle will not affect the time-averaged side force. The time-averaged side force coefficient of the body part of configuration C increases significantly behind the canard and gradually decreases near the fin, indicating that the canard increases the Magnus effect of the projectile body.

Fig. 5
figure 5

Distribution of the side force coefficient of the body

Full size image

Section x/L = 0.48 was selected to analyze the aerodynamic characteristics and the corresponding flow structures in detail because the difference in Cz is most obvious in this section, as shown in Fig. 5. Figure 6 shows the definition of the circumferential angle θ. Figure 7 gives the pressure contour, crossflow streamlines, and distribution of the pressure difference between both sides of the body. For configuration B, the asymmetric flow separation on both sides of the body contributes greatly to the −z side force, and the asymmetric separation vortices on the leeward side contribute weakly to the +z side force. For configuration C, when \(\theta\) is within 40°, the separation vortex near the y-axis on the left side is stronger than that on the right side, making the surface pressure difference point in the + z direction. When \(\theta = 40^\circ\), the separation vortex on the right side is strong, causing low pressure around the surface of the projectile, making the pressure difference point in the − z direction. When \(\theta = 70^\circ\), the left side flow separates earlier than the right side flow, and the pressure recovers; therefore, the pressure difference points in the − z direction. The asymmetric expansion wave on both sides of the surface is the reason for the + z pressure difference when \(\theta > 80^\circ\).

Fig. 6
figure 6

Schematic diagram of circumferential angle

Full size image
Fig. 7
figure 7

Pressure contours, crossflow streamlines, and surface pressure distribution curve at \(\theta = 40^\circ\), x/L = 0.48: a for configuration B, b for configuration C, and c for pressure difference

Full size image

4.1.2 Influence of Asymmetric Distortion of Separation Vortices on Body with Large Slenderness Ratio

The numerical simulation objects in this section are three Apache slender bodies with different slenderness ratios. Figure 8 shows the total side force and distributed side force coefficient of the Apache body part with different slenderness ratios at different angles of attack when M = 3.0, \(\overline{\omega } = 0.011\). The slenderness ratios of the three Apache body parts are x/d = 15, x/d = 20 and x/d = 24.88. Since it is only the body part, the side force coefficients along the axial distribution curve on the body for slenderness ratios x/d = 15 and x/d = 20 can be represented in the curve for a larger slenderness ratio x/d = 24.88. The curve of the slenderness ratio x/d = 15 corresponds to the part before x/L = 0.6 in Fig. 8b, and the curve of x/d = 20 corresponds to the part before x/L = 0.8 in Fig. 8(b). Therefore, only the side force distribution curve for x/d = 24.88 is given in Fig. 8b. Figure 8a shows that when \(\alpha \le 8.0^\circ\), the total side force and the distributed force are both negative and negatively increase with increasing angle of attack. The total lateral force increases with increasing slenderness ratios. When \(8.0^\circ < \alpha \le 12.0^\circ\), the magnitude of the side force coefficient decreases significantly and is equivalent to the magnitude at \(\alpha = 4.0^\circ\). The distributed force coefficient changes from negative to positive, which leads to a forward shift of the side force pressure center and a reversal of the total yawing moment.

Fig. 8
figure 8

Side force coefficients versus angle of attack: a total side force, b distributed side force

Full size image

Three profiles at \(x/L\) = 0.32, \(x/L\) = 0.51 and \(x/L\) = 0.91 were selected to analyze the flow field structure and conduct an in-depth study on the reversal of the side force. Figure 9 gives the pressure contour, crossflow streamlines, and distribution of the pressure difference of the body at M = 3.0, \(\alpha = 12.0^\circ\), \(\overline{\omega } = 0.011\). Combined with Fig. 9a, d, it can be seen that the asymmetric shedding vortices, secondary vortices and flow separation have significant contributions to the side force. Combined with Fig. 9b, d, it can be seen that the directions of the spin rate of the right side surface and the crossflow velocity are consistent, and the spin rate compensates for the local flow energy. Therefore, a low-pressure state is maintained after crossflow separation. The directions of the spin rate of the left side surface and the crossflow velocity are opposite. Therefore, the wall viscosity effect decreases the local crossflow velocity, and the pressure increases. Moreover, the left side secondary vortex vanishes due to dissipation. The asymmetric flow separation near \(\theta = 100^\circ\) and the negative pressure difference on the leeward side are the main causes of the − z side force. In Fig. 9b, the left side secondary vortex disappears, and the shedding vortex may be close to the surface when the axial flow develops downstream, which can be seen in Fig. 9c. The low-pressure environment of the vortex itself decreases the local pressure near the body. Moreover, the energy of the vortex also accelerates the local flow velocity and reduces the pressure. Therefore, the + z direction of the side force at the aft-body profile is induced, which is in the opposite direction compared with the cases at the forebody and midbody profiles, and the total yawing moment may change direction.

Fig. 9
figure 9

Pressure contours, crossflow streamlines, and distribution of pressure difference between right side and left side of Apache slender body, a \(x/L\) = 0.32, b \(x/L\) = 0.51, c \(x/L\) = 0.91, d pressure coefficient difference in + z direction

Full size image

4.1.3 Influence of the Fins Installation Angle on the Body Side Force

In this section, the force characteristics of the body were compared when the Apache fins had installation angles (\(\delta = 1^\circ\) and \(\delta = 2^\circ\), where \(\delta = 2^\circ\) is the original shape) and no installation angle (\(\delta = 0^\circ\)) at M = 3.0, \(\alpha = 4.0^\circ \sim 12.0^\circ\), and \(\overline{\omega } = 0.011\).

Figure 10 shows the effect of the fin installation angle on the variations in the time-average side force and the distributed side force coefficients of the body part of Apache. The time-averaged side force coefficient of the body is always negative. When the fins do not have an installation angle, the time-averaged side force magnitude is larger. When the fins have an installation angle, the side force coefficient has a certain upward shift; that is, the interference of the installation angle on the body makes the time-averaged side force of the body decrease. Due to the influence of the fin installation angle, the distributed side force coefficient of the body near the fin area is no longer consistent with that of the slender body. When the fins have an installation angle, the time-averaged distributed side force coefficient of the body near the fin area first becomes positive and then becomes negative, which changes direction compared with the case at the forebody. The difference in the side force coefficient increases with increasing installation angle. Due to the interference effect of the fin installation angle, the distributed body side force increases positively near the fins, which leads to a forward movement of the side force pressure center and a decrease in the yawing moment.

Fig. 10
figure 10

Side force coefficients versus angle of attack: a side force coefficient, b distributed side force of body

Full size image

Figure 11 shows the diagram of the fin interference effect on the body side force. When the fin has an installation angle, on the one hand, the effective angles of attack on both sides of the body (left and right from the view of base) are \(\alpha - \delta\) and \(\alpha + \delta\), respectively, which will interfere with the body and induce a + z direction side force. On the other hand, in front of the rotation axis of the left fin, the high-pressure region on the windward side caused by the shock wave decreases, while the low-pressure region on the leeward side increases, thus weakening the − z body side force. The case of the right fin is opposite, and the + z body side force is generated. Behind the rotation axis of the left fin, the high-pressure region on the windward side caused by the shock wave increases, and the low-pressure region on the leeward side decreases; therefore, the − z body side force increases. The case of the right fin is opposite, and the − z body side force is generated. The above results jointly lead to the distributed body side force coefficient changing from positive to negative near the fin region.

Fig. 11
figure 11

Interference of canted fin on body side force

Full size image

4.2 Variation and Origin of Fin Side Force

4.2.1 The Influence of Body Slenderness Ratio on the Fin Side Force

In this section, three Apache configurations with different slenderness ratios and fins without installation angles are studied. When the body slenderness ratio increases, the flow structure on the windward and leeward sides changes, and the body interference on the fin side force may be different.

Figure 12 shows the variation of the relative influence of the Apache body (\(\delta = 0^\circ\)) on the fin side force coefficient with the rolling angle at M = 3.0, \(\overline{\omega } = 0.011\), and different angles of attack. Defining a fin in configuration as Fin1 and an individual fin as a single fin. The vertical coordinate in Fig. 12 is:

$$ \Delta \overline{C}_{Z} = \frac{{C_{{Z - {\text{Fin}}1}} - C_{{Z - {\text{singlefin}}}} }}{{\max \left( {C_{{Z - {\text{Fin}}1}} } \right)}}. $$
(7)
Fig. 12
figure 12

Relative influence of body on Apache Fin1 side force at M = 3.0, \(\overline{\omega } = 0.011\): a x/d = 15, b x/d = 20, c x/d = 24.88

Full size image

The side force coefficient of Fin1 takes away the side force coefficient of a single fin and is then divided by the maximum magnitude at each attack angle of Fin1. Since \(\max \left( {C_{{Z - {\text{Fin}}1}} } \right)\) in Eq. (7) corresponds to the maximum value at each angle of attack, and \(\Delta \overline{C}_{Z}\) at each angle of attack can only represent the extent of fin interference by the body at the corresponding angle of attack. It can be seen from Fig. 12 that for Apache configurations with different slenderness ratios at the same angle of attack, the curve changes with the rolling angle are basically the same. With the increase in the slenderness ratio, the interference of the body on the fin is more obvious. In the range of \(\varphi \in \left( {0^\circ ,90^\circ } \right)\), when \(\alpha = 4^\circ\) and \(\varphi < 45^\circ\), the Fin1 side force is affected by the asymmetric shedding vortices on the leeward side. The curve has some fluctuations and positive values, and the range of positive values and the magnitude increase as the slenderness ratio increases. When \(\alpha = 8^\circ\), the influence of asymmetric shedding vortices on the Fin1 side force is enhanced. For the configuration with a slenderness ratio x/d = 24.88, the influence of body interference on the Fin1 side force has a 20% increase compared with \(\alpha = 4^\circ\). When \(\alpha = 12^\circ\), the influence of body interference on the Fin1 transient side force can reach 40%, but there is only a 10% increase compared with \(\alpha = 8^\circ\). The increment at \(\alpha = 12^\circ\) is much larger when the slenderness ratio is relatively small than when the slenderness ratio is large. In the range of \(\varphi \in \left( {90^\circ ,180^\circ } \right)\), the body interference influence on the Fin1 side force is not much different at different attack angles, and the maximum contribution is approximately 25–30%.

Folding the curves in Fig. 12 along the straight line \(\varphi = 180^\circ\) and summing data in the corresponding position (\(\varphi \in \left( {0^\circ ,180^\circ } \right)\) corresponds to \(\varphi \in \left( {360^\circ ,180^\circ } \right)\)) can obtain the net contribution of the body to the Fin 1 side force in a rolling cycle, as shown in Fig. 13. \(\Delta C_{{Z - {\text{net}}}} \left( \% \right)\) could qualitatively represent the contribution of the asymmetric effect to the side force at different rolling angles. In the range of \(\theta \in \left( {0^\circ ,90^\circ } \right)\), the fin is on the leeward side, and in the range of \(\theta \in \left( {90^\circ ,180^\circ } \right)\), the fin is on the windward side. Figure 13 shows that the asymmetric effect of the forebody shedding vortex on the fin is greater when the fin is on the leeward side than when it is on the windward side. As the slenderness ratio increases, the difference in \(\Delta C_{{Z - {\text{net}}}} \left( \% \right)\) at different angles of attack becomes gradually obvious. For the configuration with a slenderness ratio x/d = 15, \(\Delta C_{{Z - {\text{net}}}} \left( \% \right)\) increases with increasing angle of attack in the range of \(\theta \in \left( {0^\circ ,60^\circ } \right)\). For x/d = 20, the \(\Delta C_{{Z - {\text{net}}}} \left( \% \right)\) is larger at \(\alpha = 8^\circ\). For x/d = 24.88, it can be seen that when at a certain circumferential angle θ in the range of \(\theta \in \left( {0^\circ ,75^\circ } \right)\), the magnitude of \(\Delta C_{{Z - {\text{net}}}} \left( \% \right)\) increases first and then decreases with the angle of attack, and it has the maximum magnitude at \(\alpha = 8^\circ\). In Fig. 12c, the transient body interference on the Fin1 side force is the largest when \(\alpha = 12^\circ\), but the net contribution in Fig. 13c is the smallest, indicating that the contribution of asymmetric separation vortices on the Fin1 side force is reduced as the angle of attack increases. In the range of \(\theta \in \left( {75^\circ ,180^\circ } \right)\), the net contribution of body interference on the Fin1 side force is positive or negative at different angles of attack, but the difference is smaller compared to when the fin is on the leeward side. The reason may be that both the span and area of the Apache fin are large, and the fin side force is mainly determined by itself and the interference effect of the adjacent fins.

Fig. 13
figure 13

Net contribution of body interference on the Apache Fin1 side force at M = 3.0, \(\overline{\omega } = 0.011\): a x/d = 15, b x/d = 20, c x/d = 24.88

Full size image

The contribution of body interference on the fin side force coefficient in a rolling cycle was analyzed above, and then the flow mechanism of body interference on the fin at a specific rolling angle was investigated. The state of \(\varphi = 21^\circ\) with a larger contribution percentage was selected. Figure 14 shows the profile at this time.

Fig. 14
figure 14

Schematic of the profile

Full size image

Figures 15 and 16 show the pressure contours and crossflow streamlines at different profiles of no fin installation angle Apache with different slenderness ratios when M = 3.0, \(\overline{\omega } = 0.011\), and \(\varphi = 21^\circ\). Although the slenderness ratio of each configuration is different, the distance between the profile and the base of the projectile is the same. The first profile is 2.88d away from the base, and the second profile is 0.48d away from the base. When the profile is close to the fin leading edge, although the shock wave and the expansion wave induced by the fin interact with the asymmetric separation vortices, the vortex structures can still be seen clearly at each angle of attack, and the influence area of the separation vortices increases as the angle of attack increases. When the slenderness ratio is small, the vortex intensity is greater, resulting in a more influential low-pressure environment. As shown in Fig. 15b, c, when x/d = 15, the left separation vortex is located in the middle of fin1 at \(\alpha = 8^\circ\). At \(\alpha = 12^\circ\), the position of the left separated vortex is equivalent to that of the fin, and the asymmetric effect is more obvious. Therefore, \(\Delta C_{{Z - {\text{net}}}} \left( \% \right)\) increases with increasing angles of attack in Fig. 13a. As shown in Fig. 15e, h, with increasing slenderness ratio, the main position of the left shedding vortex is equivalent to that of fin1 when \(\alpha = 8^\circ\). Therefore, compared with the configurations with a small slenderness ratio, there will be an obvious vortex structure in the fin area at a smaller angle of attack for the configurations with a large slenderness ratio.

Fig. 15
figure 15

Pressure contours and crossflow streamlines for different profiles: a–c at profile x/d = 12.12 profile, d–f at profile x/d = 17.12, g–i at profile x/d = 22

Full size image
Fig. 16
figure 16

Pressure contours and crossflow streamlines for different profiles: a–c at profile x/d = 14.52, d–f at profile x/d = 19.52, g–i at profile x/d = 24.4

Full size image

In Fig. 16, when the profile is close to the fin trailing edge, due to the interaction between the shock expansion waves and the separation vortices at the fin leading edge, the left side separation vortex is destroyed, and the influence of the low pressure region induced by the vortex on the fin surface pressure is weakened. However, the right side separation vortex still affects the fin surface pressure distribution. When \(\alpha = 12^\circ\), it can be found from Fig. 16. (c), (f) and (i) that as the slenderness ratio increases, the position of the vortex gradually moves away from the body, and the dissipation of the vortex is more intense. The low-pressure environment caused by the vortex is weaker, while the low-pressure environment of the vortex merges with the low-pressure environment caused by the angle of attack on the fin leeward, weakening the effect of asymmetric shedding vortices on the pressure distribution on the fin; thus, its net contribution to the fin side force is reduced. Therefore, the magnitude of \(\Delta C_{{Z - {\text{net}}}} \left( \% \right)\) at \(\alpha = 12^\circ\) is lower than that at \(\alpha = 8^\circ\) in Fig. 13b, c, and the decrease in \(\Delta C_{{Z - {\text{net}}}} \left( \% \right)\) is more obvious when the slenderness ratio is larger. The fin span is much larger than the body diameter, and the blocking effect of the body on the flow around the fin is relatively weakened (see \(\theta \in \left( {90^\circ ,180^\circ } \right)\) in Fig. 13).

In summary, for the Apache configuration with a large slenderness ratio, when the axial flow develops downstream, the shedding vortices dissipate obviously, and the intensity of vortices decreases. After interacting with the front shock wave and expansion wave of the fin, the shedding vortices cannot maintain their structure and vanish. However, the asymmetry of the shedding vortices is enlarged, which may contribute to the side force. With the increase in the slenderness ratio, an obvious vortex structure will appear in the fin area at a smaller angle of attack. When the main part of the separation vortices is located near the fin, the contribution of vortices to the fin side force is the most obvious. When the angle of attack further increases, the contribution of the asymmetric effect to the side force of the fin will decrease.

4.2.2 Influence of Installation Angle on Fin Side Force

In this section, three Apache configurations with different fin installation angles are studied. Figure 17 indicates the effect of the fin installation angle on the distributed time-averaged side force coefficients for Apache when M = 3.0, \(\alpha = 4^\circ \sim 12^\circ\), and \(\overline{\omega } = 0.011\). The result obtained by integrating the distributed force coefficient along the x-axis is the time-averaged side force coefficient. When the fin has no installation angle, the distributed time-averaged force coefficients of the body part are negative, and the distributed time-averaged force coefficients near the fin area are positive. The positive values in the fin area are much larger than the negative values in the body part. Therefore, the time-averaged side force coefficient is positive, and the magnitude is large. When the fin has an installation angle, the distributed time-averaged side force coefficient in the fin region has a negative decrease, and the amount of side force reduction in the fin area increases as the installation angle increases. When the installation angle is \(\delta = 2^\circ\), the time-averaged fin side force changes direction, and its magnitude is reduced by at least 2 to 3 times when referring to the resulting Fig. 10.

Fig. 17
figure 17

Distributed side force coefficients for Apache when M = 3.0, \(\overline{\omega } = 0.011\): a \(\alpha = 4.0^\circ\), b \(\alpha = 8.0^\circ\), c \(\alpha = 12.0^\circ\)

Full size image

It can be seen from Fig. 18 that the transient fin side force will produce periodic fluctuation while spinning; therefore, the position with a large transient difference is selected for analysis. Taking the case at \(\alpha = 8^\circ\) and \(\varphi = 135^\circ\) as an example, the influence of the installation angle on the fin side force is analyzed. Figure 18 shows that the transient side force decreases with increasing installation angle. The position of Fin1 is shown in Fig. 19. Figure 20 gives the pressure contours on the windward and leeward sides of Fin1 when M = 3.0, \(\alpha = 8^\circ\), \(\overline{\omega } = 0.011\), and \(\varphi = 135^\circ\). On the windward side, the pressure behind the shock wave decreases and the pressure on the leeward side increases when the fin has an installation angle, and the change in pressure increases with increasing installation angle. This indicates that the fin installation angle decreases the fin effective angle of attack during the rotation movement, and the induced + z direction side force decreases.

Fig. 18
figure 18

Fin1 side force coefficients with rolling angle at M = 3.0: a with installation angle \(\delta = 2^\circ\), b with installation angle \(\delta = 1^\circ\), c without installation angle

Full size image
Fig. 19
figure 19

Schematic of Fin1 when \(\varphi = 135^\circ\)

Full size image
Fig. 20
figure 20

Pressure coefficient contours of fin1 of Apache: a with installation angle \(\delta = 2^\circ\), b with installation angle \(\delta = 1^\circ\), c without installation angle

Full size image

5 Conclusion

The aerodynamic characteristics and flow field structures of different configurations while spinning were obtained in this study, and the effect of aerodynamic components and aerodynamic interference between components on the Magnus effect were analyzed. The contents include the aerodynamic interference of the canard on the body, the aerodynamic characteristics of a large slenderness ratio projectile, and the influence of the fin installation angle on the body and the fin itself. The results show that:

  1. 1.

    For the projectile body, the canard-induced distortion of the expansion wave on both sides of the body, leeward separation vortices and secondary vortices are the main sources of side force, the magnitude of which increases compared with the configuration without canard.

  2. 2.

    For the large slenderness ratio projectile body, the left side secondary vortex at the aft-body vanishes at a certain angle of attack. The left side shedding vortex on the leeward side is close to the surface and produces a low-pressure region, thus inducing a reversal of the side force and yawing moment. Although the shedding vortex on the leeward side dissipates seriously when developing downstream, it still causes an asymmetric impact on the leeward fin. When the position of the vortex is equal to the fin, the contribution of the vortex to the side force is the largest, and the corresponding flight angle of attack decreases with the increase of slenderness ratio.

  3. 3.

    When the fin does not have an installation angle, it will not affect the time-average side force of the projectile body. When the fin has an installation angle (inducing counterclockwise spin from the view of the base), the areas of high- and low-pressure regions before and behind the rotation axis are different. Therefore, the time-averaged side force decreases, the pressure center moves forward, and the yawing moment decreases and may even change direction. The side force is reduced when the fin has an installation angle. An appropriate fin installation angle can effectively control the pressure center position of the total side force and the magnitude of the yawing moment.