1 Introduction

Origami, the ancient art of paper folding, owing to its multistability, auxetic behavior (negative Poisson's ratio), tunable mechanical characteristics, and scalability, has found diverse applications across engineering domains, including architecture, robotics, aerospace, and biomedical engineering [1]. Particularly for biomedical designs, the capability of origami to transition from a folded to a deployed form is especially intriguing [2]. Recent advancements in self-folding technologies hold promise for the development of innovative, minimally invasive treatments [3]. Also, due to its advantages, such as decreased friction, the elimination of lubricants, enhanced precision, and ease of downsizing, origami-based technologies can be used in the construction of deployable, adaptable, and lightweight structures [1].

A particularly interesting type of rigid origami is the Miura fold. The Miura fold enables deployment in a series of steps, at each of which the parallelogram is entirely planar. Due to this unique characteristic of the Miura fold, its mechanical responses have been the focus of various recent studies. A thorough theoretical investigation of the three-dimensional elastic response of a single layer of Miura-ori periodic pleated sheet was carried out by Wei et al. [4]. Lv et al. conducted additional research on the geometry of Miura-folded plates and reported the coexistence of both positive and negative Poisson’s ratios [5]. Miura-ori sheets can also be stacked to construct curved origami structures with excellent morphing and self-locking capabilities [6]. Furthermore, multi-stable elastic behaviors [7] and a reduction in structural weight [8] were accomplished with the Miura-ori pattern as well. A culmination of all these unique mechanical characteristics of the Miura fold was the development of origami-inspired mechanical metamaterials by Schenk and Guest [9]. In their study, Miura-ori metamaterials with artificial structures were found to possess auxetic mechanical properties. This was owing to the geometry of their unit cell rather than the properties of each component. The characteristics of these origami-based metamaterials, which are determined by their structure, can be tuned to meet specific needs, making Miura-ori metamaterials a viable choice to address a plethora of engineering challenges [10,11,12,13].

The research for origami-inspired mechanical metamaterials has primarily been focused on materials with inherent flexibility and ductility. However, many of the high strength materials used in aerospace, ballistic armor, prosthetics, and other medical fields are typically brittle. Especially in biomedical applications, brittle materials such as ceramics are often used due to their high corrosion resistance and biocompatibility. Therefore, to leverage origami engineering in biomedical applications, it is essential to investigate the mechanical response (crack behavior) of ceramic-based origami metamaterials. The primary concern in the mechanical response of brittle materials is their tendency to undergo catastrophic failure rather than a graceful failure mode. An ingenious solution to this problem can be found in nature. Nacre, the inner, iridescent layer of molluscan shells (also known as the mother of pearl), is a composite material constituted mainly of brittle materials. However, owing to its alternating layers of aragonite platelets and organic material film, the composite material itself demonstrates high toughness [14]. Hence, some studies have attempted to mimic the nacre structure in order to induce toughness into brittle materials. Sajadi et al. mimicked the concept of coating a brittle material with a soft material by coating ceramic structures with a flexible epoxy [15]. They reported a substantial improvement in the structure’s strength and toughness over an uncoated structure and demonstrated that the improvement is the result of the ability of the epoxy polymer to stop crack interconnection, thus preventing catastrophic failures. Polymeric interlayers, most notably polystyrene, have also been shown to improve the ballistic performance of multi-layered ceramic armors [16]. While polymer coatings and interlayers can prevent catastrophic failure, not all polymers are inherently biocompatible. One of the key possible applications of origami ceramics is in the biomedical field. Therefore, it is essential that any polymer used to prevent catastrophic failure is also biocompatible. One such potential polymer is polydimethylsiloxane (PDMS), a widely known biocompatible silicone elastomer.

In this work, we explore the possibility of inducing flexibility into ceramic-based brittle material through the art of Miura-ori metamaterial design. We are able to prevent the catastrophic failure of brittle ceramic metamaterials and to give them a graceful failure mode through the application of an elastomeric coating. The coating also considerably improves the toughness of the origami structures, and the enhancements are highly orientation dependent. Both monotonic and cyclic compression tests are carried out on the coated and uncoated structures in three orthogonal directions. The failure mechanisms are analyzed through optical and SEM micrographs. All experiments are complemented by finite-element analysis (FEA) to reveal the inherent mechanics of the anisotropic enhancements in different orientations.

2 Methods

2.1  Fabrication of coated ceramic origami structures

The 3D origami structure was generated as an STL file using MATLAB. (Table S1 shows the dimensions of this structure) The STL file was then sliced using Preform, and printed using the Formlabs Form 2 printer with a 405 nm wavelength, 250 mW laser. The laser spot size was 140 µm, and the layer thickness was 50 µm. The silica-filled (~70% SiO2) preceramic resin (Formlabs Ceramic Resin V1) was used. After printing, the printed parts were separated from the build platform, the supports were removed, and then the parts were washed for 5 minutes in isopropyl alcohol (IPA). Subsequently, they were dried with compressed air to ensure that all crevices were completely dry before sintering. Next, the samples underwent sintering in an oven according to the protocol described in the next section 'Results and Discussion'. The firing schedule is given in Table S2, and the dimensions of the structure after sintering is shown in Table S3. Finally, the structure is coated with PDMS, which is obtained as a two-part resin as the SYLGARD™ 184 Silicone Elastomer Kit. The two-part resin is mixed at a 10 to 1 ratio by mass and de-aired inside a vacuum desiccator. To apply the PDMS coating, the origami structure is dipped inside a beaker containing the de-aired solution inside the desiccator under vacuum. The thin coated structure is then pre-cured [17] at 60 °C for 35 min in an oven. To ensure the sufficient thickness of the coating (75 to 100 µm), the precured sample is once again dip-coated in the PDMS solution under vacuum, followed by full curing at 150 °C for 10 min in the oven.

2.2 Compression tests

Quasi-static monotonic and cyclic compression tests are performed on both the asymmetric uncoated and coated origami structures in three orthogonal directions and X-direction, respectively. The final origami structure has extended edges in the Z-direction for the convenience of conducting the Z-orientation monotonic loading tests. A universal testing apparatus is used for these tests (Instron ElectroPuls E3000, USA). All the tests are carried out at room temperature. The crosshead speed is maintained constant at 1 mm per minute. Load–deflection data is gathered using sensors mounted on the upper jaw. The area under the load–deflection curve is used to calculate the amount of energy absorbed.

2.3 Scanning electron microscopy

The morphology and fracture surfaces are examined using the FEI Helios Scanning Electron Microscope, courtesy of Rice University Shared Equipment Authority (SEA). An accelerating voltage of 1 kV and 50 pA current is used. In order to prevent electrostatic charging, the sample surfaces are coated with a 0.1 kÅ thickness of gold using the Denton Desk V Sputter system.

2.4 Numerical method

The explicit finite element code ABAQUS/Explicit, along with appropriate element deletion algorithms, is employed to simulate both the quasi-static monotonic and cyclic compression tests on the uncoated and coated origami structures. The origami structure was redesigned in SolidWorks, mimicking the STL file created by MATLAB, which is then exported as a STEP 203 file, and imported to ABAQUS, where it is placed between two planar discrete rigid surfaces for the numerical simulation of both tests. The concrete damaged plasticity model (CDPM) is used to simulate the behavior of the ceramic, and the Arruda–Boyce model is used to simulate the PDMS. Some of the key aspects of the two material constitutive models are given here.

2.4.1 Material constitutive models

Concrete damaged plasticity model (CDPM). The concrete damaged plasticity model, introduced by Lubliner et al. [18] and modified by Lee and Fenves [19], provides a general method for modeling quasi-brittle materials. Concrete’s inelastic behavior is represented by concepts of isotropic damaged elasticity in conjunction with isotropic tensile and compressive plasticity [20]. The yield criterion and the flow function are the two major plasticity functions in CDPM.

The yield condition under a multiaxial stress state is defined by the yield criterion, which takes into account the differing evolution of strength under tension and compression and is defined as follows in terms of effective stresses [20]:

$$F=\frac1{1-\alpha}\left(\overline q-3\alpha\overline p+\beta\left(\widetilde{\varepsilon^{pl}}\right)\left\langle{\widehat\sigma}_{max}\right\rangle-\gamma\left\langle-{\widehat\sigma}_{max}\right\rangle\right)-{\overline\sigma}_c\left(\widetilde{\varepsilon_c^{pl}}\right)=0$$
(1)

where \(\overline{p }\) and \(\overline{q }\) are the hydrostatic pressure expressed in terms of effective stress and the Mises equivalent effective stress, respectively. \(\langle \bullet \rangle\) is the Macauley bracket defined as \(\langle x\rangle =\frac{1}{2}\left(\left|x\right|+x\right).\) The parameters α, β, and γ of Eq. (1) are calculated using Eqs. (2), (3), and (4), respectively.

$$\alpha =\frac{\left({\sigma }_{b0}/{\sigma }_{c0}\right)-1}{2\left({\sigma }_{b0}/{\sigma }_{c0}\right)-1}$$
(2)

Here, \({\sigma }_{b0}/{\sigma }_{c0}\) is the ratio of the compressive strength under biaxial loading to the uniaxial compressive strength.

$$\beta =\frac{\overline{{\sigma }_{c}}\left(\widetilde{{\varepsilon }_{c}^{pl}}\right)}{\widetilde{{\sigma }_{t}}\left(\widetilde{{\varepsilon }_{t}^{pl}}\right)}\left(1-\alpha \right)-\left(1+\alpha \right)$$
(3)

where \({\overline\sigma}_c\left(\varepsilon_c^{pl}\right)\) and \({\overline\sigma}_t\left(\varepsilon_t^{pl}\right)\) are the effective cohesion stresses for compression and tension, respectively.

$$\gamma =\frac{3\left(1-{K}_{c}\right)}{2{K}_{c}-1}$$
(4)

\({K}_{c}\) is the ratio of the second stress invariant on the tensile meridian to that of the compressive meridian at the initial yield for any pressure invariant value such that the maximum principal stress is negative.

The concrete damaged plasticity model assumes non-associated potential plastic flow. The flow potential \(G\) used for this model is the Drucker-Prager hyperbolic function:

$$G=\sqrt{{\left(\epsilon {\sigma }_{t0}\text{tan}\psi \right)}^{2}+{\overline{q} }^{2}}-\overline{p}\text{tan }\psi$$
(5)

where \(\psi \left(\theta ,{f}_{i}\right)\) is the dilation angle measured in the p-q plane under high confining pressure and is the angle between the plastic potential line and the horizontal (p is the hydrostatic pressure stress and q is the Mises equivalent effective stress).   \({\sigma }_{t0}\left(\theta ,{f}_{i}\right)={\left.{\sigma }_{t}\right|}_{{\tilde{\varepsilon }}_{t}^{pl}=0,{\dot{\epsilon }}_{t}^{pl}=0}\) is the uniaxial tensile stress at failure, taken from the user-specified tension stiffening data, and \(\epsilon \left(\theta ,{f}_{i}\right)\) is a parameter, referred to as eccentricity, that defines the rate at which the function approaches the asymptote (the flow potential tends to a straight line as the eccentricity tends to zero).

The non-linear behavior of concrete in ABAQUS is defined by the following features: damage variable, yield criterion, hardening/softening rule, and flow rule.

Table S4 and S5 summarizes the values of various parameters of the concrete damaged plasticity model, which are used in numerical simulations to model the behavior of the silica ceramic. Because no viscoplastic regularization is required, the viscosity parameter in ABAQUS is set to its default value of zero.

The elastic modulus of the material decreases as it degrades. The concrete damaged plasticity model assumes that the reduction of the elastic modulus is given in terms of a scalar degradation variable, \(d\), as

$$E=\left(1-d\right){E}_{0}$$
(6)

where \({E}_{0}\) is the initial (undamaged) elastic modulus of the material. This expression holds both in the tensile \(\left({\sigma }_{11}>0\right)\) and the compressive \(\left({\sigma }_{11}<0\right)\) sides of the cycle. The stiffness degradation variable, \(d\), is a function of the stress state and the uniaxial damage variables, \({d}_{t}\) and \({d}_{c}\). For the uniaxial cyclic conditions, ABAQUS assumes that

$$\left(1-d\right)=\left(1-{s}_{t}{d}_{c}\right)\left(1-{s}_{c}{d}_{t}\right)$$
(7)

where \({s}_{t}\) and \({s}_{c}\) are functions of the stress state that are introduced to model stiffness recovery effects associated with stress reversals.

The tension and compression degradation variables can be calculated using Eq. (6). The elastic strain can be calculated using the following equation:

$${\varepsilon }_{0c}^{el}=\frac{{\sigma }_{c}}{{E}_{0}}$$
(8)

Then, the inelastic strain is calculated using:

$${\tilde{\varepsilon }}_{c}^{in}={\varepsilon }_{c}-{\varepsilon }_{0c}^{el}$$

ABAQUS converts the inelastic strain to plastic strain using the equation

$${\tilde{\varepsilon }}_{c}^{pl}={\tilde{\varepsilon }}_{c}^{in}-\frac{{d}_{c}}{\left(1-{d}_{c}\right)}\frac{{\sigma }_{c}}{{E}_{0}}$$
(9)

The magnitudes of the tensile and compressive degradation variables are given by Eq. (6), and the damage is characterized by a scalar degradation variable (\(d\)) that can be expressed in terms of the compressive (\({d}_{t}\)) and tensile (\({d}_{t}\)) degradation variables.

$$d=\left(1-{d}_{t}\right)\left(1-{d}_{c}\right)$$
(10)

The resulting input data for modeling ceramic (silica) behavior in ABAQUS are given in Table S6-S9.

Arruda-Boyce model. The Arruda–Boyce model is one of several models used to simulate hyperelastic materials. This model is based on the statistical mechanics of a material with an element of a representative volume containing eight chains in diagonal directions. The strain energy potential of the slightly extended Arruda–Boyce model to account for compressibility has the form [21]:

$$U=\mu \sum_{i=1}^{5}\frac{{C}_{i}}{{\lambda }_{m}^{2i-2}}\left({\overline{I} }_{1}^{i}-{3}^{i}\right)+\frac{1}{D}\left(\frac{{J}^{2}-1}{2}-\text{ln}J\right)$$
(11)

where,

$${C}_{1}=\frac{1}{2}, {C}_{2}=\frac{1}{20}, {C}_{3}=\frac{11}{1050}, {C}_{4}=\frac{19}{7050}, {C}_{5}=\frac{519}{673750}$$

Here, µ represents the shear modulus at small strains and \({\lambda }_{m}\) the locking stretch at which the upturn of the stress–strain curve would rise significantly. \(D\) represents double the inverse bulk modulus at small strains, i.e.,

$$D=\frac{2}{K}$$
(12)

The Arruda–Boyce model only requires two parameters, \(\mu\) and \({\lambda }_{m}\), to determine the deviatoric behavior and a single coefficient, \(D\), to control compressibility. For incompressible materials, the parameter \(D\) can be set to zero. The parameters have a physical interpretation, and the model is stable (no negative stress–strain slopes) for positive coefficient values [21, 22].

Bulk Sylgard 184 PDMS [23] is the material used in the experiment, and it is cured at a temperature of 150 °C. The density of this PDMS is \(0.965 {\text{gcm}}^{-3}\). It has been demonstrated that the Arruda-Boyce model adequately simulates the deformation of PDMS [24]. The uniaxial stress–strain data from Figure S1 are converted to true stress in ABAQUS and are used to assess the parameters of the Arruda–Boyce model. The model has been tested to ensure stability under all uniaxial tensile and compressive strains. By comparing the actual stress–strain behavior of PDMS to that predicted by the Arruda–Boyce model using the parameters listed in Table S10, we ensure that the predicted response closely resembles the actual behavior.

2.4.2 Element deletion

Element deletion is one of the most frequently used techniques for modeling material failure and separation due to fracturing in commercial finite element method software. When the necessary condition for element deletion is satisfied during the deformation, the element deletion method will remove the element volume. A given set of conditions can be used to remove an element using element deletion. The element deletion method can prevent the overestimation of stress and strain values by deleting cracked elements during simulations, which alleviates the stress concentration at the cracked surface [25]. Additionally, the impact of mesh size dependency can be lessened if small enough elements are used [26, 27]. Since the two materials used in this study have very different mechanical behaviors, i.e., brittle ceramic and hyperelastic PDMS, different modeling methods have been used for the element deletion of each material.

The “Concrete Failure” keyword feature of ABAQUS is used for element deletion in the ceramic. This keyword can be used without subroutine functions to explicitly define failure criteria and element deletion in the CDP model.

For the PDMS, due to the lack of a material failure mechanism in the ABAQUS/Explicit hyperelastic models, we created a particular user material subroutine with a maximum principal strain failure criterion to regulate the element deletion in the skin model during the tests. The VUMAT subroutine file is written in FORTRAN. Although numerous failure models exist for structural materials, the maximum stress, maximum shear stress, and von Mises stress models are the most frequently employed ones. By writing the subroutine “VUSDFLD,” the element deletion method is used to make the material fail. Any element that has a maximum principal strain that exceeds the critical strain value is removed from the analysis [28, 29]. Element deletion proved essential to prevent excess element distortion.

2.4.3 Mass scaling

Semi-automatic mass scaling is employed to make the simulation run in a reasonable amount of time. Distortion is a serious problem caused by excessive mass scaling, which cannot be evaluated solely based on the excessive distortion of elements [30]. The response for a quasi-static process should be as slow as possible without producing an inertia effect. Energy output can be used to verify that the rate of panel deformation does not dominate the response, for example, by ensuring that the ratio of kinetic energy (ALLKE) to internal energy (ALLIE) is not excessively high—typically less than 10% for most of the quasi-static analysis [20, 30]. Figure S2 demonstrates that the kinetic energy (ALLKE) of the origami structure is lower than its internal energy (ALLIE) throughout the duration of the simulation.

2.4.4 Mesh

The solid ceramic structure is divided into simpler parts and meshed using a hexahedral mesh. The PDMS coating on the ceramic origami is simulated using ABAQUS CAE’s skin feature. The membrane shell type is used for the skin. The elements in the ceramic core, coating, and jaws have an approximate global size of 0.5 and curvature control with a maximum deviation factor of 0.1. For the solid ceramic, an 8-node linear brick element (C3D8R) is used, which has reduced integration, 3 degrees of freedom at each node, and enhanced hourglass control. A 4-node 3-D bilinear rigid quadrilateral element (R3D4) type is used for compressing pair of jaws. The PDMS coating is discretized by a 4-node quadrilateral membrane element with reduced integration and enhanced hourglass control (M3D4R). The mesh of the silica ceramic is three-dimensional, while the two-dimensional mesh is used for the PDMS. The total number of elements in the final mesh was 297,000. In order to make sure the results converged for the chosen mesh density, a mesh convergence study was conducted, and we found that beyond this point, the variation in reaction force with increasing mesh size is less than 5% (Figure S3).

The actual clamps’ mass is assigned to each rigid jaw using ABAQUS’ inertia. The total reactive force acting on the upper jaw is calculated using kinematic coupling between the upper jaw and a reference point. The effect of gravity is assigned to the system since the density of the ceramic is significant.

3 Results and discussion

A single Miura-ori cell (Fig. 1a) contains four creases that intersect at a point and four identical parallelogram faces. Four independent factors describe this cell: two-panel lengths (a and b), a sector angle (φ), and a folding angle (θ) [31, 32]. For our study, we have set the parameters as a = 7 mm, b = 6.76 mm, φ = 75°, and θ = 120° (Figure S4) [31]. A Miura-ori sheet is formed by repeating a single-unit cell three times in the Z-direction. The sheet is then connected to its mirror image, creating a single tube (Fig. 1a). The aligned assembly of these tubes creates what is known as an aligned coupling, and when these aligned couplings combine with their mirror images, it forms a zipper coupling (Fig. 1b). The final 3D Miura-ori structure (Fig. 1c) is a combination of multiple aligned and zipper-coupled tubes and has a relative density of 49.5%. A video depicting this entire assembly process is presented in Supplementary Movie 1. The 3D origami model for finite element analysis (FEA) and the STL file for additive manufacturing are created using MATLAB and SolidWorks. The dimensions of the resulting origami structure are given in Table S1. Quasi-static compression tests (monotonic and cyclic) are carried out at three orthogonal orientations to investigate the mechanical properties of the origami metamaterials (Fig. 1d). Finally, to demonstrate flexibility, a cyclic compression test is carried out in the X-direction.

Fig. 1
figure 1

The assembly of the origami structure and the directions for performing compression tests. a The design begins with a single unit cell, which is replicated thrice to form a Miura sheet consisting of three-unit cells, and finally, two of those sheets are combined to form a 3-unit tube. b Three of the tubes from (a) are assembled in aligned coupling (left), and then two aligned coupled tubes are assembled with each other via zipper coupling (right). View from XZ plane, Y-direction is into the page. c The final 3D Miura-ori structure. d Schematics showing the three orthogonal orientations of the origami structure in which monotonic compression tests are carried out and the single direction in which the cyclic compression test is carried out

Full size image

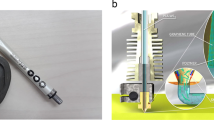
Machining ceramic is challenging owing to its brittle nature and high hardness; complicated designs, such as origami, add to the difficulties. The casting of a ceramic structure is also not as practical because of its extremely high melting temperature. 3D printing is a manufacturing philosophy that permits the flexible preparation of complex and accurate structures that are impossible to accomplish by casting and machining. In this work, we utilize slurry-based stereolithography (SLA) [33], a photopolymer resin-based 3D printing technique, to fabricate complex origami ceramic structures. The ceramic resin consists of finely dispersed ceramic (silica) particles within a UV-curable photopolymer matrix. The origami structure is then produced by irradiating the liquid suspension using ultraviolet light. The thickness of each panel in the origami construction is kept at 2 mm, which is the thinnest feature (highest resolution) that could be consistently printed. Parts with thinner features would either split and fall off mid-printing due to self-weight or break apart during support removal. The as-printed “green part” must undergo a burnout process to remove the polymer, followed by sintering to achieve the desired packed density (Fig. 2a). The samples of the origami structure are heated in accordance with the firing schedule presented in Fig. 2a and Table S2 which is slightly adjusted from the recommendations by Formlabs, USA [34]. The first burnout hold at 240 °C removes the polymer matrix that the ceramic resin prints with. At this stage, the ceramic particles have not yet fused and are loosely held together as a powder body. This phase should be long enough to completely remove the polymer matrix. Partial burnout will cause vapor pressure to increase during the ramp phase, resulting in cracks and distortion as vapor escapes. A short secondary hold at 300 °C ensures that all polymer is burned out before Ramp 2 [34]. Ramp 2 heats up the part to the sintering temperature of 1271 °C at a ramp rate of ~ 3 °C per minute. Finally, to ensure fully sintered ceramic parts with minimal crack formation within the complex origami architectures, we double the sintering hold and half the cooldown rate from the recommended 5 min and 1 °C per minute to 10 min and 0.5 °C per minute, respectively. The structures undergo a mass shrinkage of 32.6% during sintering, indicating the complete burnout of the polymer. Anticipating the shrinkage of the structure, slightly greater dimensions compared to those given in Table S1 are fed into the SLA 3D printer. The resulting dimensions of the sintered ceramic origami structure are provided in Table S3. By examining SEM images of the surface (Fig. 2b and c left), it can be observed that the structure contains silica nodules before the polymer burnout. These nodules fuse together during sintering, leading to the fully densified, sintered ceramic structure with clearly defined grain boundaries (Fig. 2d and c right).

Fig. 2
figure 2

Fabrication of the 3D-printed ceramic Miura-ori structure, followed by the application of a hyperelastic coating. a 3D printing and sintering process to produce ceramic origami structures: (from left to right) Stereolithography (SLA) 3D printing with supports, as-printed “green part” after support removal, temperature profile for polymer burnout, sintering hold, and cooldown; fully densified sintered ceramic part. (b–d) SEM images showing the morphology of the printed structure surface before (b and c-left) and after sintering (d and c-right). Before sintering, the silica is seen in powder form, which transforms into clearly refined grains in the fully sintered part. e The structure is dipped in a beaker containing a de-aired solution of polydimethylsiloxane (PDMS) inside a desiccator under vacuum to ensure uniform coating. f Photograph of the coated structure. g Optical images of the coated and uncoated structure near the creases showing that the coating reached all the corners. h Cross-section SEM image showing that the PDMS coating thickness is 75 ~ 100 µm on average

Full size image

The ceramic part is subsequently coated with an elastomeric coating of PDMS to induce flexibility in the structure. The structure is coated by dipping it inside a de-aired PDMS solution under vacuum (Fig. 2e). The coated origami structure is shown in Fig. 2f, and the vacuum ensures that the coating reaches all the corners (Fig. 2g). A section of the coated ceramic, as viewed under SEM, is depicted in Fig. 2h. The coating is seen to be nearly uniform, and the average thickness is determined to be 75 ~ 100 \(\upmu\) m from the SEM images using ImageJ. This coating is thin enough that the structure retains its hollow geometry as shown in Figure S5. It is also evident from the SEM images that the PDMS does not infiltrate the ceramic body (Fig. 2h). This means that any toughening effect due to the presence of the coating will not be intrinsic [35, 36]. Notably, the coated structure contains 91 vol.% ceramic (SolidWorks estimate), which is close to that of nacre (~ 95%), indicating a possibility of nacre-like toughening mechanisms within the structure [15, 37].

Next, we investigate the variation in mechanical properties at different orientations of the ceramic origami architecture due to geometry, as well as the enhancements due to the elastomeric coating. The structure was printed at an arbitrary orientation, which is distinct from the three orthogonal orientations in which the mechanical properties will be measured (Fig. 2a top left). This ensures that the printing orientation does not have a substantial effect on the anisotropy of the mechanical properties. Figure S6 shows the isotropic morphology of the printed structures before and after sintering. Figure 3 shows the experimental results from the quasi-static monotonic compression test. As is evident from the force-compressive strain curves, Fig. 3a–c, the origami structure, both with and without coating, demonstrates maximum strength and toughness in the Z-direction and is the weakest in the X-direction among the three directions in which compression testing is conducted. This difference in toughness can be attributed to geometric toughening; the toughness can be increased by simply flipping the orientation of the origami structure from X to Z. The sudden drop in reactive force in the load–displacement graphs corresponds to the failure of the structure and the jaw losing contact with the structure. The uncoated ceramic structure fails catastrophically in the X- and Y-directions. In the Z-direction, the ceramic structure can withstand the greatest peak force, which is a measure of the structure’s strength. Ceramic, like other brittle materials, is stronger in compression than in tension. This is because the size of the plastic crack-tip region is not particularly noteworthy due to the closure of transverse cracks, and the exceptional strength under compression is primarily a result of the ceramic’s strong bonds. Owing to the fact that cracks can propagate under tension, the diminutive size of the crack-tip plastic region hurts the strength of the ceramic. The fracture strain of the uncoated origami is also substantially larger in the Z-direction than in the X- and Y-directions. In the X-direction, the area of the structure in contact with the compressing jaws is minimal, and a substantial bending load (a combination of tension and compression) acts on the vast bulk of the structure. In the Z-direction, the area in contact with the jaws is the greatest, and most of the structure is under compressive load. As a result, the compressive portion of the total load is the greatest in the Z-direction and the least in the X-direction.

Fig. 3
figure 3

Results of the experimental quasi-static compression test on the architected ceramic structure (both uncoated and coated) in the three orthogonal directions. a–c Force-strain graph in the a X, b Y, and c Z directions, respectively. d Corresponding energy absorptions of the uncoated and coated ceramic structures in the three directions. The percentage enhancement in energy absorption due to coating is shown for each loading direction. e Optical image of the uncoated and coated origami structure at the moment of 5% compressive strain, showing catastrophic failure on the uncoated structure and graceful failure on the coated structure. f SEM images of the fracture surfaces of (i) uncoated and (ii) coated structures. The crack freely propagates over the rough surface of the uncoated ceramic and quickly reaches the surface, leading to catastrophic failure. On the contrary, the PDMS coating stops the crack for the coated sample in (ii), as shown in the inset

Full size image

The force-compressive strain response of coated and uncoated origami structures differs substantially. Li et al. observed that the number of peak stresses on the reactive force curve was equal to the number of layers in the origami during a compression test [38]. Multiple peaks in Fig. 3a indicate that the coated origami structure experiences compartmental failure (one compartment failed after another) in the X-direction, each compartment being a layer of origami, with the lowest compartment failing first. The increase in toughness due to the PDMS coating is quite dramatic in the X-direction, as shown by the energy absorption bar chart in Fig. 3d. In contrast, the effect of the coating is the least in the Z-direction. The increase in toughness is primarily attributable to the coating’s ability to prevent premature catastrophic failure. The maximum load the coated structure can support increases in all three directions. The presence of elastomeric coating hinders the propagation of cracks. While the uncoated origami undergoes catastrophic failure at ~ 1.5% compressive strain, even at ~ 5% compressive strain, only the lowest compartment fails in the coated origami. Figure 3e shows the uncoated and coated origami structure when 5% compressive strain is applied to them. Figure 3f contains SEM images showing the fracture surface morphology of the (i) uncoated and (ii) coated origami structures after they have undergone compression tests in the X-direction. The coating appears to have arrested crack propagation, stopping the cracks before they could reach the edges. In the case without the coating, the cracks tend to spread to the edges like an avalanche. Both SEM images confirm the ability of the PDMS coating to improve the toughness of the coated origami extrinsically by slowing down and eventually stopping the propagation of cracks. A zoomed-in image of the crack is shown in the inset of Fig. 3f(ii).

To further investigate the inherent mechanics leading to the various enhancements due to orientation and coating seen in the experiments, we carry out FEA to find stress distribution and identify stress concentration regions and potential failure regions. Figure 4a–c present the numerical modeling results for the quasi-static monotonic compression tests on the coated and uncoated origami samples in all three directions as the reactive load on the upper jaw versus the applied compressive strain. Good agreement in trends can be seen between the experimental and numerical results (compared with Fig. 3a–c). In the numerical modeling results, the coated ceramic origami is found to endure a greater reactive peak force than the uncoated ceramic origami structures, and the areas under the force–displacement curve are also larger in all three directions for the coated structures, as shown in Fig. 4d. Similar to the experimental results, the uncoated origami also fails catastrophically at low strains in the X- and Y-directions during the numerical simulation. The increase in energy absorbed is most pronounced in the X direction. Both the uncoated and coated ceramics have larger strengths in the Z-direction, as also observed in the experimental results.

Fig. 4
figure 4

Results of the numerical modeling of the quasi-static monotonic compression test on the architected ceramic structure (both uncoated and coated) in three orthogonal directions. a–c Load-compressive strain behavior of uncoated and coated ceramic structures in the a X direction, b Y direction, and c Z direction. d The corresponding energy absorption of uncoated and coated ceramic structures in the three orthogonal directions. e, f Von Mises stress distribution on the e uncoated and f coated ceramic. g Damage parameter distributions for the ceramic: left uncoated, right coated, top compression, bottom tension. h, i Maximum principal plastic strain (PE) distribution on the h uncoated and i coated ceramic. The Mises stress distribution is plotted for the same reactive load for coated and uncoated, while the damage parameters and the maximum principal plastic strain are shown on the ceramic for the same compressive strain of ~ 1.5%

Full size image

Although the trends in the simulations are similar to the experiments, as shown in Figure S7, the reactive forces are, however, higher in the numerical results at each strain in all three directions. This is likely because, in real samples, there are pores and manufacturing defects, which result in lower densities and higher fragilities, which are not present in the simulated material. Moreover, the real samples underwent shrinkage during sintering and are slightly smaller than the designed samples used in the numerical simulation. While it would be superior to model the exact dimensions tested in experiments, ceramic shrinkage is unpredictable and non-uniform, and the complex architecture of the origami structure limits the measurements that can be made. The percentage increase in energy absorption in the X direction is higher than the experimental results because in simulations the PDMS was modeled as a “skin” with 0 offset from the ceramic surface, but in experiments, there can be voids from air bubbles trapped between the ceramic and PDMS coating which can lead to non-uniform offset and hence a weaker interface. The uncoated and coated origami structures demonstrate similar load-strain responses at small strains, but they differ for higher strains. We have also shown in previous works that at low strains, elastomeric coating does not substantially change damage parameters [15]. Compartmental failure of the coated origami when loaded in the X-direction resulted in the multiple peaks shown in Fig. 4a in a way that is comparable to the experimental findings.

The von Mises stress generated in the uncoated and coated ceramic structures at an instance when the compressive force is the same on both structures is depicted in Fig. 4e, f (PDMS coating not shown for clarity, to highlight the stress on the ceramic part). The grey color band shows the highest stress concentration region in the structures. The maximum stress in the coated origami is substantially less than in the uncoated ceramic structure. Comparing the stress at the upper facets in the insets of Fig. 4e, f, it is evident that the coating has transferred the stress across the facets from the corners where the stress concentration occurs. This prevents the stress at the vertex from reaching the fracture stress and the subsequent formation of cracks.

Since the PDMS skin is assumed to have 0 offset between the ceramic and the coating, the displacement of the ceramic and coating is assumed to be equal at the interface [39]. The von Mises stress on the coating is much smaller than on the ceramic for the same displacement because the coating has a lower elastic modulus. Figure 4g shows the distribution of damage parameters in the coated and uncoated ceramic structure under the same applied strain of 1.5% in the X-direction. The magnitudes of both the tensile and compressive damage parameters are greater on the uncoated origami than the coated origami, which is consistent with the smaller stress concentration in the coated origami seen in the von Mises distribution above. For both coated and uncoated origami, the tensile and compressive damage parameter concentrations occur in different regions of the facets: the tensile damage parameter is high in the area of the facet where the angle between adjacent planes is larger, and the compressive damage parameter is high in the region where this angle is lower. The tensile damage parameter is higher in the area where the tensile stress is higher, and the compression damage parameter is higher in the region where compressive stress is high. Moreover, in both coated and uncoated origami, the tensile damage parameter is substantially lower than the compressive damage parameter. This indicates that the internal stress generated is mostly compressive rather than tensile in both coated and uncoated. However, the decrease in the maximum tensile damage parameter due to coating is almost twice as high as the decrease in the maximum compressive damage parameter, indicating that the improvement in toughness is more due to the alleviation of tensile stress than compressive stress in their respective stress concentration regions. This could be partly responsible for the most substantial improvement of toughness in the X-direction over the other two directions since the proportion of stress developed as tensile is greatest when the origami is compressed in the X-direction.

Figure 4h - i show the maximum principal plastic strain (PE) distribution on the uncoated and coated ceramic for the same applied strain of 1.5% when loaded in the X-direction. The orientation of the cracks is assumed to be perpendicular to the maximum principal plastic strains; consequently, the maximum principal plastic strains are used to visualize the direction of the cracking [40]. Figure 4h - i depict the cracking pattern on both the uncoated and coated structures at the point of failure of the uncoated structure, with the applied strain being the same for both. The cracks initiate from the middle of the intersection of two facets and propagate to the facets along the panel lengths. When the ultimate load is reached, cracks appear abruptly. It is clear from the maximum principal plastic strain surface plots that the coating effectively hinders crack propagation in regions where tensile damage is dominant, as well as in areas where compression damage is prevalent. The concentration of the maximum principal strain is high on both the tensile and compressive stress concentration regions in the uncoated origami structure discussed above. However, on the coated ceramic, even though the magnitude of the maximum principal plastic strain is substantially smaller everywhere, there is no concentration of the plastic strain in the region where tensile stress is dominant, which is due to the greater reduction in tensile stress concentration by the presence of the coating.

In both the experiment and the numerical simulation, it is observed that the failure of the coated origami initiates along the bottom region of the origami when loaded in the X-direction. Compartmental failure occurs in the coated origami, and the uncoated origami fails abruptly in the middle. In both simulations and experiments, the failure is initiated at the regions where the facets form a smaller adjacent angle. The lowest compartment always fails first because the turning effect of forces on both sides cancels each other at the contact points of the valley, while that is not the case at the edges, and as a result, large lateral displacement occurs at the edges. Hence, origami undergoes compartmental failure, starting with the flattening of the bottom layer.

Finally, since the X-direction is the most compliant orientation, we carry out cyclic tests on the coated origami structure in the X-direction. The cyclic loading is done up to 1.5% compressive strain because the uncoated samples consistently fail before ~ 1.5% compressive strain. The load strain graph of the quasi-static cyclic compression test is given in Fig. 5. The first curve in Fig. 5a represents the origami structure’s initial loading. The area under the loading and unloading graphs differ considerably for the first cycle and then roughly equalizes for subsequent cycles. The first cycle’s loading curve is similar to the monotonic compression test. However, during unloading, the stiffness decreases and does not follow the loading curve, indicating that transverse cracks have closed irreversibly. When loaded again, the stiffness increases and follows a path similar to the unloading curve of the first cycle, indicating that most of the transverse cracks have closed. Peak force appears to decrease with increasing cycle number. The decrease in maximum load in each new cycle is due to crack bridging and the formation of larger cracks [41].

Fig. 5
figure 5

Experimental and numerical results of the quasi-static cyclic compression test on the coated origami structure in the X direction. Variation of reactive load with the applied compressive strain for three cycles of quasi-static cyclic compression test from experiments (a) and from numerical simulations (b)

Full size image

Numerical simulations are also carried out for these cyclic tests. In the numerical simulation, the uncoated origami structure failure starts below 1.5% strain, so cyclic compression tests are conducted up to a displacement of ~ 1.5% strain on the coated origami structure. A tabular amplitude function with zero smoothening is used to change the direction of the feed after every half cycle. The variation of displacement of the compressing jaw with time is given in Figure S8. There are no signs of failure anywhere, although compressed to a strain of 1.5%, which is beyond the failure point of uncoated origami in the monotonic quasi-static compression test. In the numerical results (Fig. 5b), the area between the unloading and loading curves decreases for each increase in cycle number. This means energy absorption decreases with an increasing number of cycles, agreeing with experimental results. However, the reactive forces are higher in the numerical results, as was the case for static tests. This is again likely because the simulated material lacks the pores and manufacturing flaws found in real samples, which may have led to higher fragilities. Additionally, the real samples are marginally smaller than the designed samples used in the numerical simulation due to non-uniform shrinkage that occurred during sintering. The intricate architecture of the origami structure restricts the measurements that can be taken and hence makes it difficult to account for the unpredictable ceramic shrinkage in the simulated structures. However, despite these differences between the simulations and experiments, the trend of peak load slightly decreasing with increasing cycle number is achieved similar to the experimental results.

4 Conclusion and future work

In summary, the potential for creating origami structures using brittle materials is demonstrated through 3D-printed Miura-ori ceramic structures. The asymmetric increase in toughness owing to the origami structure is shown through experiments and numerical simulations of quasi-static monotonic and cyclic compression tests. The ceramic origami structure, when coated with an elastomeric coating, shows orientation-dependent enhancement in toughness in terms of both failure strain and energy absorption in comparison to the uncoated structure. Stress surface plots on the ceramic structure show that the coating efficiently disseminates stress over the facets of the coated origami, relieving the corners from the high stress that would otherwise happen in an uncoated origami structure. The increased toughness of coated structures is also a result of a hindrance to the propagation of cracks in the brittle ceramic. Catastrophic failure is prevented as the crack propagation is hindered by the elastomeric coating. FEM analysis of the compression tests reveals that stress is transferred away from the critical high-stress regions resulting in smaller maximum stress in the structure. Moreover, the hindrance to the propagation of cracks by the presence of coating is also apparent from the FEM results in surface plots of maximum principal plastic strain. This work can encourage further research to understand the mechanics of origami engineering involving brittle materials. Building on the insights gained from this study, several avenues can be pursued to further enhance the design and functionality of origami structures for brittle materials. One potential direction is to optimize the dimensional parameters of the Miura-ori unit cell. The current study focused on one particular 3D Miura-ori structure produced from fixed parameters such as panel lengths (a, b), sector angle, and folding angle, which effectively demonstrated toughness enhancement. However, by adjusting these parameters through optimization techniques, the mechanical response could be tailored to suit particular application needs, whether for maximizing energy absorption, impact resistance, crack resistance, etc. Optimizing these structural parameters could also yield more compact or lightweight designs with low relative densities without compromising strength. The optimization schemes that need to be applied to achieve those specific performance goals are also a promising research field. Techniques like Bayesian optimization or genetic algorithms could help efficiently explore the design space and identify optimal configurations [42,43,44]. These advancements could lead to the development of robust, versatile, and application-specific origami structures, pushing the boundaries of what is possible with brittle materials.