Abstract
In the present study, Soil Conservation Service -Curve Number (SCS-CN) method, Earth Observation (EO) data sets and Geographic Information System (GIS) have been used in order to estimate the surface runoff from Jhagrabaria an agricultural watershed of Allahabad district, Uttar Pradesh (India). LANDSAT-7ETM+, NOAA data and hydrologic soil groups have been used to prepare land use/land cover, rainfall and soil map. The traditional SCS-CN method for calculating the composite CN is very tedious and time demanding process of the hydrologic modeling. Therefore, GIS is now being used in combination with the SCS-CN method. The outcome of work showed 79.35 (CNII) of normal condition, of dry condition 61.76 (CNI) and of wet condition 89.84 (CNIII), respectively. This investigation outline that ungauged watershed exhibits an annual average of 14 years runoff volume as 3.58 × 106 m3 from an average annual rainfall of 14 years 110.77 cm and the average annual surface runoff of 14 years was 23.83 cm and annual average runoff coefficient of 14 years was 0.22. The correlation analysis suggests that the strong correlation as R 2 (0.91) was observed between satellite drive rainfall and runoff from SCS-CN method. The developed rainfall–runoff model for the region will be useful to understand the watershed and its runoff flow characteristics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Often, the hydrological studies needs records of rainfall and runoff to understand the management of water. Watershed characteristics which may be most readily compared to estimate the volume of runoff that will result of rainfall, soil type and land use/land cover (LULC).
The application of conceptual hydrological models in ungauged watersheds or watersheds with limited data to generate runoff records for planning and design purposes is intriguing [8, 17]. In such applications, the hydrological models are calibrated to gauged watersheds of a homogeneous region, and regional equations helps in explaining the variations of the model parameters with physiographic factors. However, the uncertainty of calibrated model parameters is high enough to simulate the hydrologic response of ungauged watersheds with reduced efficiency [8].
Earth Observation (EO) data and Geographical Information System (GIS) together have played a critical role in watershed modeling [19] in general and rainfall-runoff modeling [6, 12, 32] in particular. Many studies have proved the use of EO data namely groundwater [27, 46, 48, 51, 52], river water quality [55], coastal water [22], lake and wetlands [5, 47, 53, 59, 60], land use/land cover mapping [45, 46, 48, 50, 51], land use change trajectories [56], land use/land cover modeling [28, 49], urban land use dynamics [4], hydrological modeling [31], forest mapping [44], cyclone tracking [16], soil characterization [37], climate change [54], slope estimation [57], landscape ecology [47, 53], ocean studies [35, 36] and watershed management [67], watershed prioritization [68]. GIS processing has become a critical step in hydrologic modeling since it contributes to generate model parameters in a spatially distributed manner. It has involved in data storage, retrieval, map overlay, spatial map analysis etc. and to derive hydrologic parameters from soil, land cover, and rainfall etc.
The SCS-CN method has been widely used since the availability of tabulated curve number (CN) values for rainfall-runoff model [7, 34, 66]. Moore and Clarke [26] showed that a variety of distributions can be easily incorporated into this type of model structure and they derive analytical equations for the responses of different distributions. Hosking and Clarke [14] has extended Moore and Clarke work, to show how the model can be used to derive a relationship between the frequencies of storm rainfall and magnitude of peak flows in an analytical form. Moore [25] examines the case where the stores/lose of water to deep drainage and evapotranspiration. Recent work at the UK Institute of Hydrology has shown the model applications for long runs to derive flood frequencies [11, 23], and also in a more distributed application with radar rainfall and snowmelt inputs for flood forecasting.
Ahmad and Verma [2] have successfully integrated SCS-CN method with EO data into GIS platform and estimated runoff for Kharun River sub-basin. Köylü and Geymen [21] applied SCS-CN method to calculate the runoff in the catchment basin of the Yamula Dam (Kızılırmak River of Turkey) and found SCS-CN method is sensitive to LULC change and change of CN (change of the runoff values). Chavda et al. [9] implemented SCS-CN method for estimation of surface runoff and water availability for two sites in Junagadh, Gujarat and suggested surface water harvesting structures. Topno et al. [63], also computed annual runoff depth for ungauged catchment area (Vindhyachal region) and revealed that the SCS-CN method can be used to estimate surface runoff depth when adequate hydrological information is not available. Thomas [61] implemented SCS-CN method over Olifants River catchment (South Africa) area with the help of EO data and GIS and generated spatially distributed infiltration maps for the catchment. Muthu and Santhi [30] applied SCS-CN method over Indian region (Thiruporur Block, Kancheepuram district) using seven rain gauge station data and generated seasonal variation of rainfall runoff of the study area. Ningaraju et al. [33] also used this model over ungauged (Kharadya milli watershed, Mandya district of Karnataka) watershed and found a good co-relationship (R 2 = 0.94) between estimated runoff and rainfall for 11 years of datasets. Aldoma and Mohamed [3]; simulated rainfall runoff process for Khartoum state (Sudan) using SCS-CN method and EO data as input of model and found SCS-CN method is capable for predicting runoff. Tirkey et al. [62], estimated runoff (for Jharkhand, India) using SCS-CN method and compared with observed runoff and found a strong correlation between rainfall and runoff as well as between observed runoff and estimated runoff with high accuracy of runoff estimation by SCS-CN method. Fan et al. [13] have developed a simulation model based on the SCS-CN method to analyze the rainfall-runoff relationship in Guangzhou (in southern China). Xianzhao and Jiazhu [66], estimated runoff during flood period from small watershed in Loess Plateau of China using SCS-CN method and found SCS-CN method is legitimate and can be successfully used to simulate the runoff generation and the runoff process of typical small watershed. Khosravi et al. [20], accept SCS-CN method as better (due to easiness of model) than other empirical models and compared nine empirical models (which were independent from LULC and soil data) with SCS-CN method base runoff.
The aims of the work were as follows: (i) to calculate daily runoff (mm) using CN method and (ii) to find out optimal empirical mathematical model (EMM) with respect to SCS-CN, EO data sets and GIS based model for generating annual runoff (cm) in ungauged Jhagrabaria an agricultural watershed of Allahabad district, U.P. (India).
Materials and Methods
Study Area
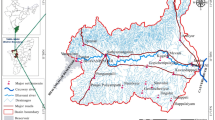
The Jhagrabaria watershed is lies in latitudes 25°12″-25°20″ N and longitudes 81°33″-81°44″ E with an area of 150.06 km2 (Fig. 1) in district Allahabad of state Uttar Pradesh, India. The area is dominated by sandstone and shale of Upper Vindhayan formations. The slope of area shows a nearly flat to a gentle undulating topography with occasionally small hillocks. The elevation ranges from 90–180 m above mean sea level [43].
Data Sets Used and Methdology
The comparative specification of LANDSAT TM and ETM+ sensors are given in Table 1. LANDSAT-7ETM+ of month June, 2006 was downloaded on October 2, 2012, and it was distorted with scene line error and which was rectified using gap filling program in ENVI 4.8 software. Generally, the atmospheric effect is not corrected by data providers; it should be done by the users as a pre-processing task [29]. It was geometrically corrected using Survey of India (SOI) topographic maps (1:50,000, 63G/11 and 63G/12). The ground-truth work (150 ground-truth data/reference data) was performed in the month of August 2012. LULC types namely fallow land, barren land, vegetation and water bodies/wetlands were identified and their co-ordinates were logged with a hand held Global Positioning System (GPS) device (Garmin (eTrexH), with ±15 m horizontal locational accuracy. These data were used in supervised classification method [43]. For ‘salt and pepper’ noise correction from classified image, a majority filter with a 3 × 3 window size was used.
The soil map was obtained from National Bureau of Soil Survey and Land Use Planning (NBSS and LUP), Nagpur, Maharashtra, India. The map was scanned and then geo-referenced with help of SOI topographical maps. Further, the geo-referenced soil map was digitized and soil attributes were assigned.
The rainfall data of entire duration and area was derived from daily rainfall satellite data as provided by the National Oceanic and Atmospheric Administration (NOAA) were downloaded from web-portal. The need of satellite estimated rainfall arises mainly due scare to rain gauges [40]. The daily rainfall estimate is provided for the South Asia (70°-110° E; 5°-35° N) beginning from May 01, 2001. The product is updated three times daily at around 9.00 a.m., 1.00 p.m. and 9.00 p.m. eastern local time and covers a 24-h period of accumulated rainfall. Resolution of rainfall estimates is 0.1°×0.1° and inputs include GTS station data, as well as GOES GPI infrared cloud top temperature fields derived from Meteosat and polar orbiting satellite rainfall estimate data from SSM/I on board defense meteorological satellite program and AMSU-B on board NOAA15, 16 and 17 [40,41,42] (Fig. 2).
Description of SCS-CN method
In the early 1950s, the United States Department of Agriculture (USDA), NRCS (later named as Soil Conservation Service, SCS) developed a method to estimate the volume of direct runoff from rainfall. It is often referred as the curve number (CN) method, was empirically developed for small agricultural watersheds. Analysis of storm event rainfall and runoff records indicates that there is a threshold which must be exceeded before runoff occurs. It is expressed mathematically (Eqs. 1–8) as follows [64]:
where, F is actual retention after runoff begins, mm; S is watershed storage, mm (S ≥ F); Q is actual direct runoff, mm; P is total rainfall, mm (P ≥ Q); I is initial abstraction, mm.
The amount of actual retention can be expressed as:
The initial abstraction defined by the NRCS mainly consists of interception, depression storage, and infiltration occurring prior to runoff. Necessity of estimating both parameters I and S in the above equation, the relation between I and S was estimated by analyzing rainfall runoff data for many small watersheds [64]. The empirical relationship is:
Substituting Eq. 3 into Eqs. 1 and 2
It is a rainfall runoff equation used by the NRCS for estimating depth of direct runoff from storm rainfall. The equation has one variable P and one parameter S. S is related to CN by:
where, CN is a dimensionless parameter and its value ranges from 1 (minimum runoff) to 100 (maximum runoff).
Its determination is based on the following factors: hydrologic soil groups, land use, land treatment, and hydrologic conditions. The NRCS runoff equation is widely used in estimating direct runoff because of its simplicity and flexibility.
SCS soil scientists, classified soils into four hydrologic soil groups namely A, B, C and D (Table 2) [64], depending on infiltration, soil classification and other criteria. Land use and treatment classes are used in the preparation of hydrological soil cover complex, which are used to estimate direct runoff.
Antecedent moisture conditions (AMC) (Table 3) is an indicator of watershed wetness and availability of soil moisture storage prior to a storm, and can have a significant effect on runoff volume. Recognizing its significance, SCS has developed a guide for adjusting CN according to AMC based on the total rainfall in the 5-day period preceding a storm. Three levels of AMC are used in the CN method: AMC-I for dry, AMC-II for normal and AMC-III for wet conditions. Table 3 gives seasonal rainfall limits for these three AMC. The CN values are documented for the case of AMC-II [64]. Based on the McCuen and Richard [24], the composite CN can be computed by using the following equation [64]:
where, CNII is the composite CN, CNi is the CN from 1 to any number, Ai is the area with curve number CNi and A is the total area of watershed.
where, CNII (normal condition), CNI (dry condition) and CNIII (wet condition).
Determination of CN Value
The CN has potential of runoff estimation. Under the same precipitation condition, low CN values mean that the surface has a high potential to retain water whereas high value mean that the rainfall can be stored by the land surface only to a small extent. Therefore, areas with high CN value will produce a large amount of direct runoff and thereby contributed strongly to the flood peak. CNII is the CN of normal condition, CNI is the CN of dry condition, CNIII is the CN of wet condition. Calculated CNn values from a given AMC condition are tested by plotting the rainfall and runoff data pairs, and the calculated rainfall runoff curves.
SCS-CN Method for Runoff
Several methods are available for estimation of runoff. Among them, the United States Department of Agriculture (USDA), SCS-CN method is the most popular and widely used [18, 39]. Simplicity, predictability, stability and its reliance on only one parameter namely the CN have few advantages of this method. LULC classes can be integrated with the HSGs of the sub basin in GIS environment and the weighted CN can be estimated. These estimated weighted CN for the entire area can be used to compute runoff. The main inputs required to the SCS-CN method are delineation of the watershed boundary, preparation of soil map, preparation of LULC map and AMC to estimate daily runoff.
Model Verification
In order to validate the SCS-CN method output, we used daily rainfall data of 14 years. The observed runoff data was not available; hence, we used the rainfall data as the proxy data. The validity and feasibility of the SCS-CN method based on the GIS was verified by comparing the estimated runoff with daily rainfall peaks. The results showed that the hydrographs of the estimated runoff process and the peak of rainfall coincided very well, even though the model may have higher uncertainties and less precision and low practicability due to non availability of the observed runoff.
Results and Discussion
Land Use/Land Cover (LULC)
Overall accuracy was >86.79% and Kappa statistics (0.80) [43]. LULC map of the watershed was classified into four classes namely; vegetation, fallow, barren and water bodies (Fig. 3a). It was observed that a 36.1% (or 24.59 km2) of total watershed area falls into barren land and 24.4% (or 36.62 km2) is allocated to fallow land. These two classes and the wetlands/water bodies mainly consists the non productivity land category (Fig. 3b). In our classification analysis, we found that not more than one-third of the study area is under vegetation. This is primarily due to recurrent water flooding and logging. The fallow, barren and fallow lands together forms the highest area, i.e. 48.99% of the total watershed area whereas nearly equal area (i.e. 47.81%) comes under vegetation condition. This is a sign of a model setting where the area exposed for erosion and have probability for water erosion [43]. Several studies have been conducted to demonstrate the feasibility of interpreting the land use categories from EO data and further used as input data in a hydrologic modeling for estimating the runoff [1, 38, 58].
Hydrologic Soil Groups (HSGs)
Based on infiltration rate, texture, depth, drainage condition and water transmission capacity, soils have been classified into different hydrologic soil groups: A, B, C and D. The criteria adopted for such classification is illustrated in Table 3 [10]. The soil taxonomic classes mainly consisted of Jarkhori sandy loam, Devra clay soil, Newaria loamy, stony land and Lohgara silty loam (Fig. 4a). The soil of area is divided into five different categories (according to NBSS and LUP). The watershed is mainly dominated by Newaria loam patties with 58.26 km2 (or 38.82%) area, Devra clay soils with 31.92 km2 (or 21.27%) and Jarkhori sandy loam soils 18.65% (or 27.99 km2) (Fig. 4b). Figure 4b, suggests that the soil of whole watershed is vulnerable to soil erosion during runoff of a high degree due to existence of sand fraction in large quantities. The stoniness of the land (14.63 km2 or 9.75%) will act as barrier however leading to generation of higher amount of rainfall but prevent the soil loss from runoff. These classes help in development of hydrologic soil groups (HSG) (Fig. 4c) with help of standard guide line (Section 2C-5—NRCS TR-55 Methodology) [15, 65]. The area under a different HSG in study area was estimated. Figure 4 d areal expenses of different HSGs in the study area (km2 and in %). Overall, the HSG ‘D’ occupies the major portion of the study area. Thus, this indicates that the study area has very slow runoff potential but the HSG ‘A’ also occupies the large portion of area hence area have high runoff.
Rainfall (2002–2015)
The daily rainfall data of period 2002–2015 is shown in Fig. 5a and b. Figure 5c showed rainfall map of 20 August 2003, according to it the area comes under four zones (each zone represents to pixel value or rainfall value of 20 August 2003), and therefore it is not required to draw THESSIEN polygons because rainfall is in already distributed format. The area is characterized by low, irregular and erratic rainfall pattern. Minimum annual runoff was recorded in the year 2004 with 86.2 cm (drought year over India) and 2002 with 90.8 cm (due to drought year) and annual runoff in the year 2013 with 51.63 cm (Table 4).
a Showing an example of the merged analysis of daily precipitation (rainfall) for the month of July 20, 2001. The merged analysis presents similar spatial distribution patterns with those of satellite estimates while its magnitude is close to the gauge-based analysis over areas with gauge data, b shows a final product after merging the inputs and (c) Shows rainfall (from satellite final product) of August 20, 2003
Figure 6a and 6b showed rainfall of per day and monthly rainfall of 14 years. In general, there is low rainfall (<60 cm annually) in the year 2004, 2009, 2010 and 2015. Hence, severe to moderate drought was occurred in 2004, 2009, 2010 and 2015. The monthly rainfall, runoff, and runoff coefficient of period 2002–2015 is presented in Table 4 and Fig. 6b. It was observed that highest monthly rainfall event were recorded in August 2013, and September 2003 with 54.14 cm (and 17.19 cm runoff) and 48.19 cm (12.10 cm runoff), respectively. Table 4 and Fig. 6b showed that September 2015 was recorded lowest monthly rainfall as 4.32 cm (during the monsoon). This trend coincides with moderate drought (less amount of rainfall or less annual rainfall 95.0 cm). Further, analysis showed that October rainfall was highest monthly rainfall as 30.5 cm (with 15.2 cm runoff) in 2013, 7.4 cm in February 2013, 8.9 cm in March 2015 and 5.0 cm in April 2015 in non monsoon season. The result shows slight level of variation especially in September monthly rainfall from 2003 to 2015.
Runoff and Runoff Coefficient (2002–2015)
CNII is the CN of normal condition (Fig. 7a and b), CNI is the CN of dry condition (Fig. 7c and d), CNIII is the CN of wet condition (Fig. 7e and f). Figure (7a–f) is showing destitution of CNn at spatial extent and corresponding histogram showing destitution of CNn at pixels wise (n = I, II and III) in images. Calculated CNn values from a given AMC condition are tested by plotting the rainfall and runoff data pairs, and the calculated rainfall runoff curves as shown in Fig. 7g.
Figure 8a represents seasonal trend, indicated the variability trends of runoff and runoff coefficient (C R). It was observed high C R (is inversely proportional of rainfall) during June 2005 (0.56, because runoff was more than 55% of rainfall), August 2005, September 2007 (0.6, highest value of C R due to higher value of runoff and higher value of runoff because of saturated soil due to high percentage of rainfall in August 2007) and June 2011 (0.52) because during these months runoff was high (>51% of total rainfall of the month) (Fig. 8a and Table 4). Thirty-three out of 56 months of monsoon season showed C R above 0.2 (below 0.2, less runoff most and a large part of rainfall seep into soil) because during of these months, the area receives good amount of rainfall but most of the percentage of total rainfall has converted into runoff. Figure 8a has also revealed that during monsoon season from 2002 to 2015, 21 rainfall events have given more percolation time because during these rainfall events C R ≤ 0.2. Above groundwater recharge line (>0.2) most of rainfall event gives more runoff or low absorption process therefore June and July rainfall improves groundwater recharge. From Table 4 and Fig. 8a has two times (June 2010 and September 2015) C R reach to zero due to no rainfall.
From Fig. 8b and Table 5, the average annual rainfall, runoff, annual runoff coefficient and annual runoff volume of area were estimated as: 110.77 and 23.83 cm, respectively with average annual runoff coefficient as 0.204 of period 2002 to 2015 means 21.5% of average annual rainfall was used to recharge groundwater during the last 14 years and average annual volume runoff was 3.57 × 107 m3 become wastewater from study area during 2002–2015. Table 5 has also revealed that total annual rainfall and runoff of study area was 1550.77 cm, and 333.63 cm respectively, but annual runoff coefficient (0.22) does not change much from average runoff coefficient (0.204). But total annual water loss in the form of total annual volume runoff (5.0 × 108 m3) from study area was higher than average annual volume runoff (3.57 × 107 m3) during period 2002–2015.
Rainfall Runoff Correlation Analysis
After analysing the relationship between total rainfall, average surface runoff and average runoff volume, the relationship between rainfall and runoff was observed. The relationship between rainfall and the surface runoff is depends on number of factors relating to the watershed and climate, but in our analysis we assumed that other factors are uncountable due to lack of ground observed data sets. The correlation coefficient was found to be 0.91 (due to small study area) (Fig. 9), Tirkey et al. [62] also find good coefficient of determination (0.891) for large area therefore SCS-CN model can handle properly small as well as large study area.
Conclusion
The non availability of measured runoff arrest direct comparison between computed with the measured runoff at of Jhagrabaria ungauged agricultural watershed. However, based on HSGs obtained from soil classification, LULC, SCS-CN method and GIS made possible to measure runoff depth (cm or m) and runoff volume (m3) at ungauged watershed. The composite CN for normal condition is 79.35 (CNII), for the dry and wet conditions are 61.76 (CN1) and 89.84 (CNIII), respectively. The average annual runoff depth of period 2002–2015 is equal to 23.83 cm (or 0.23 m), and the total area of the watershed is 150.06 km2, the average annual volume of water was 3.58 × 106 m3, which represents 21.50% of the average annual rainfall (110.77 cm or 1.11 m) of 14 years. The SCS-CN method satisfactorily computes the runoff for the available rainfall events in the Jhagrabaria watershed. The conventional hydrological data are generally not available for the purpose of the design and operation of water resources systems at the watershed or sub-watershed level, in such cases, EO and GIS can serve as better techniques for the estimation of runoff, watershed hydrology characteristics, geomorphology, slope, etc. Surface runoff and sediment losses are the two important hydrologic responses from the rainfall events occurring over the watershed systems. Rainfall generated runoff is very important in various activities of water resources development and management such as a: flood control and its management, irrigation scheduling, design of irrigation and drainage network, hydro power generation etc.
References
Adham M, Shirazi S, Othman F, Rahman S, Yusop Z, Ismail Z (2014) Runoff potentiality of a watershed through SCS and functional data analysis technique. Sci World J. doi:10.1155/2014/379763 1-15. Online publication date: 1-Jan-2014
Ahmad I, Verma MK (2016) Surface runoff estimation using remote sensing & GIS based curve number method. International Journal of Advanced Engineering Research and Science 3(2):73–78
Aldoma A, Mohamed MY (2014) Simulation of rainfall runoff process for Khartoum state (Sudan) using remote sensing and geographic information systems (GIS). International Journal of Water Resource and Environmental Engineering 6(3):98–105
Amin A, Amin A, Singh SK (2012) Study of the urban land use dynamics in Srinagar city using geospatial approach. Bulletin of Environment and Scientific Research 1(2):18–24 ISSN: 2278–5205
Amin A, Fazal S, Mujtaba A, Singh SK (2014) Effects of land transformation on water quality of Dal Lake, Srinagar, India. Journal of the Indian Society of Remote Sensing 42(1):119–128. doi:10.1007/s12524-013-0297-9
Bajlan A, Mahmoudian shooshtary M, Avlipoor M (2005) Monthly runoff predictions with artificial neural network (ANN) and compare its results with empirical methods in watershed kasilian, 5th Iranian Hydraulic Conference, pp. 877–885
Berod DD, Singh VP, Musy A (1999) A geomorphologic kinematic-wave (GKW) model for estimation of floods from small alpine watersheds. Hydrol Process 13:1391–1416
Chandramohan T, Durbude DG (2000) Application of remote sensing technique for estimation of surface runoff from an ungauged watershed using SCS curve number method. J Appl Hydrol 13:1–9
Chavda DB, Makwana JJ, Parmar HV, Kunapara AN, Prajapati GV (2016) Estimation of runoff for Ozat catchment using RS and GIS based SCS-CN method. Current World Environment 11(1):212–217
Chow VT, Maidment DR, Mays LW (1988) Applied hydrology. McGraw-Hill, Inc
Dorum A, Yarar A, Faik Sevimli M, Onüçyildiz M (2010) Modelling the rainfall–runoff data of susurluk basin. Expert Syst Appl 37:6587–6593
Esmaili Ouri A, Samiei M (2011) Assessment of empirical methods of runoff estimation in Tangesoye watershed in Fars provience, Articles Collections of the Seventh National Conference on Watershed Management Science and Engineering
Fan F, Deng Y, Hu X, Weng Q (2013) Estimating composite curve number using an improved SCS-CN method with remotely sensed variables in Guangzhou. China Remote Sens 2013(5):1425–1438. doi:10.3390/rs5031425
Hosking JRM, Clarke RT (1990) Rainfall-runoff relations derived from the probability theory of storage. Water Resour Res 26:1455–1463
Iowa storm water management 2C-5 Manual (2C-5 NRCS TR-55 Methodology). Version 2 (2008), www.ctre.iastate.edu/pubs/.../2C-5NRCSTR-55Methodology.pdf
Islam T, Srivastava PK, Rico-Ramirez MA, Dai Q, Gupta M, Singh SK (2015) Tracking a tropical cyclone through WRF–ARW simulation and sensitivity of model physics. Nat Hazards 76(3):1473–1495. doi:10.1007/s11069-014-1494-8
Kaleris V, Kourakos V, Langousis A (2015) Calibration of rainfall-runoff models: the effect of the temporal distribution of rainfall on uncertainties in model parameter estimation. Geophys Res Abstr 17:EGU2015–EG13543
Kashani MH, Ghorbani MA, Dinpashoh Y, Shahmorad S (2014) Comparison of volterra model and artificial neural networks for rainfall–runoff simulation. Nat Resour Res 23(3). doi: 10.1007/s11053-014-9235-y.
Khayam M, Molavi A (2004) Runoff Quantitative Analysis in Saeedabadchai watershed. Journal of Geography and development 376:78–91
Khosravi K, Mirzai H, Saleh I (2013) Assessment of Empirical Methods of Runoff Estimation by statistical test (Case study: BanadakSadat Watershed, Yazd Province). Int J Adv Biol Biomed Res 1(3):285–301
Köylü Ü, Geymen A (2016) GIS and remote sensing techniques for the assessment of the impact of land use change on runoff. Arab J Geosci 9:484
Kumar RP, Ranjan RK, Ramanathan AL, Singh SK, Srivastava PK (2015) Geochemical modeling to evaluate the mangrove forest water. Arab J Geosci 8(7):4687–4702. doi:10.1007/s12517-014-1539-z
Lamb R (1999) Calibration of a conceptual rainfall-runoff model for flood frequency estimation by continuous simulation. Water Resour Res 35:3103–3114
McCuen RH (1982) A Guide to hydrologic analysis using SCS methods. Prentice-Hall Inc., Englewood Cliffs, New Jersey, pp 145
Moore RJ (1985) The probability-distributed principle and runoff production at point and basin scales. Hydrol Sci J 30:273–297
Moore RJ, Clarke RT (1981) A distribution function approach to rainfall-runoff modeling. Water Resour Res 17(5):1367–1382
Mukherjee S, Shastri S, Gupta M, Pant M, Singh CK, Singh SK, Sharma K, Srivastava PK (2007) Integrated water resource management in Aravali Quartzite of Delhi India by remote sensing and geo-physical techniques. J Environ Hydrol 15 (10)
Mutak S, Baghmar NK, Singh SK (2015) Prediction of industrial land use using linear regression and MOLA techniques: a case study of Siltara industrial belt. Landscape & Environment 9(2):59–70
Mutak S, Baghmar NK, Singh SK (2016) Correction of atmospheric haze of IRS-1C LISS-III multispectral satellite imagery: an empirical and semi-empirical based approach. Landscape & Environment 10(2):63–74. doi:10.21120/LE/10/2/2
Muthu ACL. and Santhi MH. (2015). Estimation of surface runoff potential using SCS-CN method integrated with GIS. Indian J Sci Technol 8(28). doi: 10.17485/ijst/2015/v8i28/83324
Narsimlu B, Gosain AK, Chahar BR, Singh SK, Srivastava PK (2015) SWAT model calibration and uncertainty analysis for streamflow prediction in the Kunwari River Basin, India, using sequential uncertainty fitting. Environmental Processes 2(1):79–95. doi:10.1007/s40710-015-0064-8
Nema MK, Singh JK (2006) Runoff estimation from a small watershed using GIUH approach in GIS environment. J Soil Water Conserv 5:34–41
Ningaraju HJ, Ganesh Kumar SB, Surendra HJ (2016) Estimation of Runoff Using SCS-CN and GIS method in ungauged watershed: a case study of Kharadya mill watershed, India. International Journal of Advanced Engineering Research and Science 3(5):36–42
Pandey A, Dabral PP (2004) Estimation of runoff for hilly catchment using satellite data. Journal of the Indian Society of Remote Sensing 32:236–240
Pandey VK, Singh SK (2010a) Comparison study of ECCO2 and NCEP reanalysis using TRITON and RAMA data at the Indian Ocean Mooring Buoy point. e-Journal Earth Science India 3(IV):226–241
Pandey VK, Singh SK (2010b) Validation of temperature field within ocean data assimilation system with the Mooring Buoy’s data in the Indian Ocean. VSRD technical and Non Technical International Journal 1(4):222–234
Paudel D, Thakur JK, Singh SK, Srivastava PK (2015) Soil characterization based on land cover heterogeneity over a tropical landscape: an integrated approach using earth observation datasets. Geocarto International 20(2):218–241. doi:10.1080/10106049.2014.905639
Ragan RM, Jackson TJ (1980) Runoff synthesis using Landsat and SCS model. Journal of Hydraulic Division of the American Society of Civil Engineers 106:667–678
Ramana GV (2014) Regression analysis of rainfall and runoff process of a typical watershed. International Journal of Science and Applied Information Technology 3(1):16–26
Rawat KS, Tripathi VK (2016) Standardized precipitation index based approach for development of regional drought monitoring system. Journal of Remote Sensing Technology 4(1):48–57. doi:10.18005/JRST0401004
Rawat KS, Mishra AK, Sehgal VK (2012a) Spatial variability of satellite derived rainfall erosivity factors (R-Factors) for a watershed near Allahabad. Journal of Agricultural Physics 11(1):71–78
Rawat KS, Mishra AK, Paul G, Kumar R (2012b) Estimation of ground water recharge in Shankergarh block of Allahabad (India) using remote sensing and statistical approach. Global Journal of Science, Engineering and Technology 2(1):34–48
Rawat KS, Mishra AK, Bhattacharyya R (2016) Soil erosion risk assessment and spatial mapping using LANDSAT-7 ETM+, RUSLE and GIS-a case study. Arab J Geosci 9:288. doi:10.1007/s12517-015-2157-0
Singh SK, Kewat SK, Aier B, Kanduri VP, Ahirwar S (2012) Plant community characteristics and soil status in different land use systems at Dimapur, Nagaland, India. For Res Pap 73(4):305–312. doi:10.2478/v10111-012-0029-x
Singh SK, Pandey AC, Singh D (2014a) Land use fragmentation analysis using remote sensing and Fragstats. In: Srivastava PK, Mukherjee S, Islam T, Gupta M (eds) Remote sensing applications in environmental research, Chapter 9. Springer International Publishing Switzerland, pp 151–176. doi:10.1007/978-3-319-05906-8_9
Singh CK, Shastri S, Avtar R, Mukherjee S, Singh SK (2010a) Monitoring change in land use and land cover in Rupnagar district of Punjab using Landsat and IRS LISS III satellite data. Ecological Question Special Ed 13:73–79
Singh SK, Singh P, Gautam SK (2016a) Appraisal of urban lake water quality through numerical index, multivariate statistics and earth observation data sets. International Journal of Science and Technology 3(2):445–456. doi:10.1007/s13762-015-0850-x
Singh SK, Singh CK, Mukherjee S (2010b) Impact of land-use and land-cover change on groundwater quality in the Lower Shiwalik hills: a remote sensing and GIS based approach. Central European Journal of Geosciences 2(2):124–131. doi:10.2478/v10085-010-0003-x
Singh SK, Sk M, Srivastava PK, Szabó S, Islam T (2015b) Predicting spatial and decadal LULC changes through cellular automata Markov chain models using earth observation datasets and geo-information. Environmental Processes 2(1):61–78. doi:10.1007/s40710-015-0062-x
Singh SK, Srivastava PK, Gupta M, Thakur JK, Mukherjee S (2014b) Appraisal of land use/land cover of mangrove forest ecosystem using support vector machine. Environmental Earth Sciences 71(5):2245–2255. doi:10.1007/s12665-013-2628-0
Singh SK, Srivastava PK, Pandey AC (2013) Integrated assessment of groundwater influenced by a confluence river system: concurrence with remote sensing and geochemical modeling. Water Resource Management 27:4291–4313. doi:10.1007/s11269-013-0408-y
Singh SK, Srivastava PK, Singh D, Han D, Gautam SK, Pandey AC (2015a) Modeling groundwater quality over a humid subtropical region using numerical indices, earth observation datasets, and X ray diffraction technique: a case study of Allahabad district, India. Environ Geochem Health 37(1):157–180. doi:10.1007/s10653-014-9638-z
Singh SK, Srivastava PK, Szabó S, Petropoulos GP, Gupta M, Islam T (2016b) Landscape transform and spatial metrics for mapping spatiotemporal land cover dynamics using earth observation data-sets. Geocarto Interbation :1–15. doi:10.1080/10106049.2015.1130084
Srivastava PK, Mehta A, Gupta M, Singh SK, Islam T (2015) Assessing impact of climate change on Mundra mangrove forest ecosystem, Gulf of Kutch, western coast of India: a synergistic evaluation using remote sensing. Theor Appl Climatol 120(3):685–700. doi:10.1007/s00704-014-1206-z
Srivastava PK, Mukherjee S, Gupta M, Singh SK (2011) Characterizing monsoonal variation on WQI of River Mahi in India using GIS. Water Quality Exposure Health 2(3–4):193–203. doi:10.1007/s12403-011-0038-7
Srivastava PK, Singh SK, Gupta M, Thakur JK, Mukherjee S (2013) Modeling impact of land use change trajectories on groundwater quality using remote sensing and GIS. Environ Eng Manag J 12(12):2343–2355
Szabo G, Singh SK, Szabo S (2015) Slope angle and aspect as influencing factors on the accuracy of the SRTM and the ASTER GDEM databases. Physics and Chemistry of the Earth, Parts A/B/C 83-84:137–145. doi:10.1016/j.pce.2015.06.003
Tedela N, McCutcheon S, Rasmussen T, Hawkins R, Swank W, Campbell J, Adams M, Jackson C and Tollner E (2012). Runoff curve numbers for 10 small forested watersheds in the mountains of the Eastern United States. J Hydrol Eng :1188–1198. doi:10.1061/(ASCE)HE.1943-5584.0000436
Thakur JK, Srivastava PK, Singh SK (2012b) Ecological monitoring of wetlands in semi-arid Konya closed basin, Turkey. Reg Environ Chang 12(1):133–144. doi:10.1007/s10113-011-0241-x
Thakur JK, Srivastava PK, Pratihast AK, Singh SK (2012a) Estimation of evapotranspiration from wetlands using geospatial and hydrometeorological data in geospatial techniques for managing natural resources. Edited Book. Co Publication Springer and Capital. Edited by Thakur, Singh et al., (2012) ISBN 978–94–007-1857-9 (HB) pp. 53–67. doi 10.1007/978-94-007-1858-6_4
Thomas A (2015) Modelling of spatially distributed surface runoff and infiltration in the Olifants River catchment/water management area using GIS. International Journal of Advanced Remote Sensing and GIS 4(1):828–862
Tirkey AS, Pandey AC, Nathawat MS (2013) Use of high-resolution satellite data, GIS and NRCS-CN technique for the estimation of rainfall-induced run-off in small catchment of Jharkhand India. Geocarto International. doi:10.1080/10106049.2013.841773
Topno A, Singh AK, Vaishya RC (2015) SCS CN runoff estimation for vindhyachal region using remote sensing and GIS. International Journal of Advanced Remote Sensing and GIS 4(1):1214–1223
USDA-SCS (1986) United States Department of agriculture, soil conservation service. Urban Hydrology for small watersheds. Technical Release No. 55. Second Edition. Washington, D.C
Vaze J, Jordan P, Beecham R, Frost A, Summerell G (2011) Guidelines for rainfall-runoff modeling. eWater Cooperative Research Centre, ISBN 978–1–921543-51-7
Xianzhao LIU, Jiazhu LI (2008) Application of SCS model in estimation of runoff from small watershed in Loess Plateau of China. Chin Geogra Sci 18(3):235–241
Yadav S, Singh SK, Gupta M, Srivastava PK (2014) Morphometric analysis of Upper Tons basin from Northern Foreland of Peninsular India using CARTOSAT satellite and GIS. Geocarto Internation 29(8):895–914. doi:10.1080/10106049.2013.868043
Yadav S, Dubey A, Szilard S, Singh SK (2016) Prioritization of sub-watersheds based on earth observation data of agricultural dominated northern river basin of India. Geocarto Internation. doi:10.1080/10106049.2016.1265592
Acknowledgements
We express sincere thanks to Editor in Chief and volunteer reviewers. This work was supported by the University Grants Commission, New Delhi, India under Grant number F. No. 42-74/2013 (SR)]. Further, we are grateful to USGS for Landsat satellite data.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Rawat, K.S., Singh, S.K. Estimation of Surface Runoff from Semi-arid Ungauged Agricultural Watershed Using SCS-CN Method and Earth Observation Data Sets. Water Conserv Sci Eng 1, 233–247 (2017). https://doi.org/10.1007/s41101-017-0016-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41101-017-0016-4