Elastic lateral-torsional buckling of glass beams with continuous lateral restraints

Abstract

Lateral-torsional buckling is a typical buckling mode for slender members loaded in bending, which is characterized by the lateral and torsional displacement of the cross-section along the complete member length. Structural glass members are often connected to the encompassing structure by means of a silicone sealant joint along the member length, which acts as a partially rigid lateral connector, restraining the movement of this side of the member. While this will increase the lateral-torsional buckling resistance of these members, this is currently not considered during the design. In this paper the behaviour of glass beams with a continuously restrained top edge, loaded by a line load or central point load along this edge, will be investigated by executing a numerical parametric study. In this study, the restraint provided by the silicone sealant joint is modelled by lateral springs along the edge of the beam. The influence of the spring stiffness on the critical load and corresponding eigenmode shape will be determined in an eigenvalue analysis, considering both monolithic and laminated glass beams. The results of this study will give some first insights in the influence of lateral restraints on the lateral-torsional buckling behaviour.

Introduction

In glass structures, glass beams or beam-like elements are often used to conserve the transparency of the glass structure. As illustrated in Fig. 1, the purpose of these elements is mainly to carry gravity and wind loads on roofs, or to stiffen facades against wind load actions (Fig. 1). Consequently, these elements are mainly loaded in bending. These beams are connected with the encompassing structure using a mechanic or adhesive connection between one side of the beam and the structure. As this connection will have a certain stiffness, it will impede the lateral displacements along one of the sides of the beam, either at discrete locations or continuously. Currently, more and more researchers are focusing on adhesive connections, such as Belis et al. (2011a), Weller and Wuensch (2013), Dispersyn et al. (2014, (2015), and Santarsiero (2015). This paper will focus on continuous adhesive connections as well.

Fig. 1

Examples of beam-like element in facades (left) and roofs (right). The photos are reproduced from Christiaens (2009) and Giles Pike Architects (2016)

As these beam(-like) elements are often rather slender, they are very susceptible to lateral-torsional buckling (LTB). This is a global instability mode for a beam loaded in bending, in which the compressed part of the beam buckles. However, this movement is restrained by the part of the beam in tension, resulting in a combined lateral and torsional movement of the cross-section. The lateral restrains provided by adhesive or mechanic connections could considerably increase the LTB resistance. Up until recently, the existing research on LTB of glass beams only covered basic cases of laterally unsupported glass beams, disregarding certain advantages that are linked to current building practices. To this extent, the subject of LTB of unrestrained glass beams has been covered by multiple researchers (Luible 2004; Belis et al. 2013; Haldimann et al. 2008; Feldmann et al. 2014). However, the advantageous effect of the lateral restraints has only been covered very recently by Belis and Bedon (2014), Bedon and Amadio (2015a), Bedon et al. (2015b).

In Belis and Bedon (2014), the critical buckling moment of simply supported monolithic glass beams, loaded by a uniform bending moment and restrained laterally along their top edge, was examined. Here, a first analytical closed-form expression was proposed for the critical buckling moment $\hbox {M}_{\mathrm{cr}}$ of a beam with continuous lateral restraints. The obtained analytical $\hbox {M}_{\mathrm{cr} }$values agreed fairly well with the values obtained in numerical simulations. However, the match was not as good as it would be in later work by Bedon and Amadio (2015a), because the number of half waves n in the buckled shape was assumed to be equal to one. Based on the numerical simulations, it was found that the spring stiffness k provided by the lateral restraints should be higher than about $10^{3} \hbox {N/m}^{2}$ for the restraints to have a significant effect on $\hbox {M}_{\mathrm{cr}}$. This minimum value of k decreases with increasing beam slenderness. The advantageous effect of the lateral restraints increased with increasing values of L and decreasing values of the glass thickness. Additionally, the results of Verhoeven (2008) were proposed in this work to obtain an estimate of a realistic spring stiffness k (see Sect. 2) and the corresponding realistic amplification of $\hbox {M}_{\mathrm{cr}}$.

Fig. 2

Experiments on silicone joints. Top DC 895; bottom SG 500

Bedon and Amadio (2015a) also studied the elastic buckling behaviour of monolithic glass beams with an elastically restrained edge. A closed-form expression was formulated of the critical buckling load of a beam loaded by a uniform bending moment, taking into account that the number of half sine waves n in the buckling shape can be greater than one. The thus obtained expression for the critical buckling moment and the corresponding amplification factor matched the corresponding results almost perfectly, since the number of half waves n was found to increase with increasing stiffness of the lateral restraint. In a next step, Bedon and Amadio (2015a) studied the effect of the elastic restraint along the top of the beam for a beam loaded by a downward line load or central point load, at either the top or bottom edge of the beam. For these load configurations, a closed-form expression could not be formulated. However, for practical design purposes a conservative correction factor was proposed to determine the equivalent uniform moment for a restrained beam loaded by a line load or point load, considering realistic stiffness values k for silicone joints. This investigation was extended in Bedon et al. (2015b), where the LTB resistance of monolithic glass beams was examined in a geometric nonlinear numerical simulation. The shape and size of the geometric imperfection introduced during these simulations was found to be very important for the buckling resistance and beam deformation. Based on the results obtained for the critical buckling load and the buckling resistance, Bedon et al. (2015b) proposed an extension for the current LTB design rules valid for laterally unrestrained beams.

The expressions of $\hbox {M}_{\mathrm{cr}}$ for the critical moment of a restrained beam loaded by a constant bending moment are all based on work by Larue et al. (2007). Here, the cross-section is assumed not to deform. However, work done by Bradford (1998, (2000), as well as Vrcelj and Bradford (2009) for steel I-section beams suggests that the governing buckling mode would be lateral-distortional buckling for a beam with stiff lateral restraints and a slender web. In this buckling mode, an interaction between LTB and local buckling, the web deforms. In the current investigation, some cross-sectional distortion was also perceived, as well as local buckling of some geometries (see Sect. 5). Care should be taken that these buckling modes are not overlooked in an analytical formulation, if they were found to be relevant for realistic applications.

Table 1 Overview of shear tests on structural sealant joints

In this work, the elastic lateral-torsional buckling behaviour of both monolithic and laminated glass beams was studied in a numerical parametric study. All beams were restrained at their top edge and loaded by either a downward or upward load. The upward load was not previously considered, but is of practical importance for design. Restraining the compressed edge will be more effective than restraining the tensioned edge, and starting from a certain lateral constraint stiffness the critical load for an upward load will become considerably smaller than that for a downward load. In practice, the designer should consider both cases, but depending on the relative upward and downward load magnitudes, as well as the magnitude of the joint stiffness, the upward or downward load case can be more restricting. In this study, the behaviour will be studied for a large range of joint stiffness values k, going from an almost zero stiffness to an extremely large stiffness. This range encompasses the realistic restraint stiffness values for sealant joints obtained from two separate test series, each corresponding with a different material.

In the next section, the test series used to determine the stiffness of two different sealants joint materials will be briefly discussed. Subsequently, the parametric study will be described, followed by the numerical model used for the study. Next, the main results of the study will be presented with a focus on the effect of the lateral restraint provided by the sealant joint on the critical load, as well as the corresponding eigenmode shape.

Stiffness of sealant joint

During lateral-torsional buckling, the silicone joint between the top edge of the glass beam and the encompassing structure will deform elastically. To study the effect of these elastic lateral restraints at the top of the beam on the LTB failure of these beams, the behaviour of these joints must be determined.

During two test series at Ghent university, experiments were executed in which a silicone joint was loaded in shear. In a first test series, executed by Verhoeven (2008), the behaviour of Dow corning®  895 (DC 895) was examined. This one-component sealant, used for glass structures in practice, is described in (Dow Corning 2012). The sealant was applied between two separate steel parts, as shown in Fig. 2, which were pulled apart after sufficient curing. Two different geometries of the silicone joint were considered, as described in Table 1, with dimensions as depicted in Fig. 3. During these tests, the complete load-displacement behaviour of the silicone joint until failure was recorded. However, only the obtained stiffness values will be of importance in the current study of the linear elastic buckling behaviour. In Table 1, the obtained stiffness values are given: K is the measured stiffness; $\hbox {k\,=\,K/L}_{\mathrm{sil}}$ is the measured stiffness per unit length, for a joint width $\hbox {w}_{\mathrm{sil}}$ (assuming a constant variation of K in length direction). More details about the tests and the obtained results can be found in Verhoeven (2008), Belis and Bedon (2014), Bedon et al. (2015b).

The second test series was executed by Van Lancker et al. (2015). In this series, the Sikasil®  SG-500 (SG-500) silicone sealant was used, a two-component silicone as described by Sika (2015). In the test setup, a silicone layer was applied between two cold-formed profiles and two glass panes (Fig. 2). The two cold-formed steel shapes were then pulled apart by means of large screws connected to the steel profiles, introducing shear deformation in the silicone joints. Two types of cold formed steel elements were used: a box profile (as drawn in Fig. 2) and a C-profile. The dimensions of the silicone joints and the obtained stiffness values are given in Table 1. From the results, it is clear that the SG-500 joint is stiffer than the DC 895 joint: for a given area $\hbox {w}_{\mathrm{sil }}~ \hbox {x}~ \hbox {L}_{\mathrm{sil}}$, the SG-500 sealants will be about three times stiffer than the DC 895 sealant.

Fig. 3

Dimensions of tested silicone joints

Fig. 4

Position of the lateral restraints and considered loads

The sealant joints are applied between the top surface of the glass beam and the encompassing structure. As a first approximation, realistic stiffness values for the geometries considered during the parametric study (as specified in Sect. 3) can be determined by scaling the stiffness values k, obtained for a certain width $\hbox {w}_{\mathrm{sil,exp}}$, to the width of the silicone joint that can be used for the considered member in the parametric study. This can be done by multiplying the obtained experimental $\hbox {k}^{*}_{\mathrm{mean}}$ values from Table 1 with the joint width $\hbox {w}_{\mathrm{sil}}$. In Sect. 3.2, the range of realistic k values for the considered geometries is determined.

Numerical parametric study

Scope

The described study is limited to simply supported beams in fork supports, which can be either monolithic or laminated. The laminated beams consist out of two glass panes and an interlayer. For the interlayers, only one material is considered with a relatively low stiffness corresponding with long term loading.

The top edge of all considered beams is laterally supported by a continuous spring. At the same edge, the member is loaded by either a central point load or a constant line load. These loads are either upward or downward, so that the effect of (negative) wind-suction on the structure connected to the members is covered. The different loads and the position of the lateral restraints is given in Fig 4. It is expected that the effect of the spring stiffness will be most distinct for positive loads, the restrained top edge being the compressed edge.

Varied parameters

In the parametric study, two different cross-sectional geometries were used for the members: one monolithic cross-section (1L), and one laminated cross-section with two glass panes (2L). This is further specified in Table 2. The general dimensions and the used coordinate system are shown in Fig. 5.

For the considered geometries, the realistic range of stiffness values of the springs k per unit length can be determined based on Tables 1 and 2, as explained in Sect. 2. In practice, the sealant joint width can be locally smaller due to the presence of setting blocks which serve to keep the distance between the glass beam and the encompassing structure prior to silicone application. However this local effect is neglected. Thus, a constant width $\hbox {w}_{\mathrm{sil}}$ equal to the glass thickness t was considered for the monolithic beams (1L). For the laminated beams, it was assumed that a backfill with a maximum thickness of one glass pane might be present along the whole beam length, so that the stiffness for one laminated beam (2L) is constant, but can vary between the extreme values corresponding with widths $\hbox {w}_{\mathrm{sil}}$ equal to t and 2t. By rescaling the obtained k values from Table 1, realistic minimum and maximum values for k can be obtained (Table 3). Based on the obtained values, a realistic stiffness range for the considered geometries would be between 3 $\times$ $10^{5}$ N/m/m and 2 $\times$ $10^{6}$ N/m/m.

Table 2 Cross-sectional geometry

Fig. 5

Member dimensions and coordinate system

Table 3 Realistic stiffness values for silicone joints based on the experimental stiffness measurements

Table 4 Studied parameters

In the parametric study, a very large range of stiffness values was considered (Table 4), going from very small to very high values. While the higher stiffness values can no longer be considered as realistic for silicone sealant joints, they could be realistic for beams of which the upper edge is clamped into a stiff steel U-section. Furthermore, the investigation of the large stiffness range enables the study of the gradual change in behaviour of the beams while going from almost zero stiffness to extremely large stiffness values of the lateral restraints. The previously determined realistic stiffness values for silicone joints lie within the studied range.

For both studied cross-sectional geometries, the length L varied between six values and the height-to-length ratio h/L could attain four values. For each of these members, nine different stiffness values were selected for the lateral constraint of the top of the member (Table 4), ranging from an (almost) zero stiffness to an almost rigid constraint, encompassing the realistic stiffness values described above. Finally, each of these laterally supported members can be loaded by a positive or negative point load or line load, as depicted in Fig. 4. Consequently, an extensive group of 1728 realistic cases is considered in the parametric study.

In Appendix 2, it is detailed how the equivalent weak-axis bending stiffness $\hbox {EI}_{\mathrm{z,eff}}$ and equivalent torsional stiffness $\hbox {GI}_{\mathrm{t,eff}}$ can be calculated for laminated beams consisting out of two identical glass layers with an interlayer. These equivalent stiffness values were obtained using the sandwich theory, as described by Haldimann et al. (2008), originally from Luible (2004). Based on the equivalent stiffness values, an equivalent thickness $\hbox {t}_{\mathrm{eff}}$ can be calculated for weak axis bending $(\hbox {t}_{\mathrm{eff,EIz}})$ and torsion $(\hbox {t}_{\mathrm{eff,GIt}})$, as also specified in Appendix 2 (Eqs. 16–17). In the derivation of these values, the geometry from Table 2 and the material properties from Sect. 4.1 were used. The obtained equivalent thickness values are depicted in Fig. 6. The equivalent bending thickness $\hbox {t}_{\mathrm{eff,EIz}}$ is independent of the beam height h, but the equivalent torsional stiffness $\hbox {t}_{\mathrm{eff,Git}}$ does vary with h. Both equivalent thickness values increase with increasing L. Overall, the equivalent thickness values of the laminated beams are all larger than the thickness of the monolithic glass beam (19 mm).

Fig. 6

Equivalent thickness for weak-axis bending $(\hbox {t}_{\mathrm{eff,EIz}})$ and torsion $(\hbox {t}_{\mathrm{eff,GIt}})$

Numerical model

All elements studied in the parametric study were modelled in Abaqus 6.14-1, using inputfiles (Dassault 2014). Python 2.7 was used for the creation and execution of the parametric study, as well as for the processing of the results.

Materials

The glass was modelled as a linear elastic material with a modulus of elasticity E of 70 GPa and a Poisson’s coefficient of 0.23. For the interlayer, a (fictive) linear elastic interlayer material was introduced, with a shear modulus G of 1 MPa and Poisson’s coefficient of 0.49. The corresponding value of the modulus of elasticity E of the interlayer can be determined using Eq. 1.

$$\begin{aligned} E=2G(1+\nu ) \end{aligned}$$

(1)

In reality, the interlayer material will display a viscoelastic instead of a linear elastic behaviour. However, in the linear buckling analyses executed in this work (see Sect. 4.2), all nonlinear effects on the material behaviour are ignored and the material properties of the base state are used. To take into account the effects of long-term loading on the interlayer, a linear elastic material behaviour with a relatively low shear modulus G was introduced. The employed G value of 1 MPa lies between the long term plateau value at $20^{\circ }$C for Polyvinyl Butyral (PVB) of about 0.1 MPa and an elastic shear modulus after 30 years ($10^{9}$ s) of 4.2 MPa for $\hbox {SentryGlas}^{\textregistered }$ (SG) at $20^{\circ }$C (Bennison et al. 1999; Callewaert 2012). Only one shear modulus was considered to limit the total number of calculations in the parametric study.

Fig. 7

Mesh and point load application for monolithic (left) and laminated (right) beams with L $=$ 4 m and h/L $=$ 1/20

Fig. 8

Boundary conditions and mesh at right end of monolithic (left) and laminated (right) beams with L $=$ 4 m and h/L $=$ 1/20

Fig. 9

Position of springs and mesh at left top side of monolithic (left) and laminated (right) beams with L $=$ 4 m and h/L $=$ 1/20

Analysis step

The eigenvalue and eigenmode were determined in a linear buckling analysis (BUCKLE step), using a Lanczos eigensolver. The critical load is obtained by multiplying the eigenvalue with the applied load. The Lanczos eigensolver can be used to find eigenvalues greater than a prescribed value. If this prescribed value is chosen as zero, only the positive eigenvalues corresponding with each of the load cases displayed in Fig. 4 are returned, so that the smallest critical load corresponding with each of the four load cases is found directly. In the current study, only the first positive eigenvalue and the corresponding eigenmode are considered, as these will determine the critical buckling load and buckling shape. The obtained values are described in the next section.

Elements and mesh

The used element types and mesh sizes were the results of the convergence and validation study described in Sect. 4.6. All utilised elements were continuum elements, but the element type and mesh differed depending on the geometry of the modelled elements. For the monolithic glass panes (1L), the mesh consisted out of quadratic brick elements with reduced integration (C3D20R) and 20 nodes. A mesh size of 0.025 m was used. In the thickness direction, only one element was present (Figs. 7, 8, 9).

For the laminated beams (2L), the mesh consisted out of linear brick element with 8 nodes. For the glass, C3D8I elements were used, enhanced with incompatible nodes to obtain a better bending behaviour. For the interlayer C3D8R elements with reduced integration were chosen. Normally, C3D8RH elements would be better suited due to the near incompressible behaviour of the interlayer. However, these could not be combined with the selected Lanczos solution method of the eigenvalue problem. The mesh size was again 0.025m, but now two elements were present in the thickness direction for each layer to allow for stress variations over the interlayer thickness (Figs. 7, 8, 9). This resulted in high size-to-thickness ratio of the interlayer elements. However, the convergence and validation study showed no deviations caused by this high ratio.

Boundary conditions and loading

All modelled members were simply supported by fork supports at both ends, which restrain the sideways displacement. The boundary conditions for the right side of the beam, depicted in Fig. 8, will be discussed in the following. For monolithic glass beams, the sideways displacement (in y-direction) is restricted at one of the vertical glass edges, while for the laminated beams, this displacement is restricted at both vertical glass edges. Furthermore, the vertical displacement (in z-direction) of the glass plate(s) at the bottom of the end sections is zero for both geometries. At the left beam end the boundary conditions are similar, but one additional boundary condition is present: the displacement in x-direction of one glass node at the bottom of the cross-section must be zero.

The modelled beams were either loaded by a central point load or a distributed load. Both loads were modelled by a set of point loads on the glass layers of the beam (Fig. 7). The central point load was modelled by a set of equal point loads applied in all top nodes of the two mid-span elements of each glass layer. The distributed load was modelled by applying an equal point load in all top nodes of the glass layers of the beam. For the laminated beams, all boundary conditions and loads on the soft interlayer material were avoided to prevent excessive local deformations.

Modelling of restraints and constraints

The structural silicone joint can be simplified as a continuous lateral spring with spring stiffness k (N/m/m), safely neglecting the small torsional stiffness of the joint. In the model, this spring was represented by a row of spring elements (SPRING1) along the top nodes of one of the outer glass panes, connected with the ground (Figs. 4, 9). For the considered linear buckling analyses, the influence of the eccentricity of the springs was examined and was found not to influence the analysis results.

The applied springs only have a non-zero stiffness in lateral direction (y-direction). The stiffness of the two outer spring elements (at the beam edges) was determined by multiplying k with half the element size, while the stiffness of the other spring elements was determined by multiplying k with the full element size.

For the laminated geometries, the connection between the interlayer and glass layers in the beam is achieved by tie constraints between the adjoining surfaces of the glass and the interlayer.

Validation of the numerical model

Before validating the utilised numerical model, a convergence study was executed to select an appropriate mesh size and element type, as specified in Sect. 4.3. Next, the numerical models of the monolithic and laminated glass beams were validated by comparing the converged results obtained for the zero spring stiffness with the analytical values for the critical central point load $\hbox {F}_{\mathrm{pos}}$ and critical line load $\hbox {p}_{\mathrm{pos}}$, given respectively by Eqs. 2 and 3. The former equation finds its origin in (Standards Australia 1994), while the latter equation originates from (Van Impe 2010). In these equations, $\hbox {EI}_{\mathrm{z}}$ is the bending stiffness about the weak axis, $\hbox {GI}_{\mathrm{t}}$ the torsional stiffness, L the buckling length, and $\hbox {z}_{\mathrm{g}}$ the distance of the point of load application above the shear centre of the beam (here equal to h/2). In Eq. 3, $\hbox {c}_{1}=1.132$ and $\hbox {c}_{2}=0.459$. For the laminated beams, the calculation of the equivalent bending stiffness $\hbox {EI}_{\mathrm{z}}$ and torsional stiffness $\hbox {GI}_{\mathrm{t }}$ is specified in Appendix 2 (Eqs. 7 and  11). Overall, the maximum deviations for the point load were 2 %, while the maximum deviations for the line load were 4 %.

$$\begin{aligned}&F_{cr} =\frac{16.8}{L^{2}}\sqrt{EI_z GI_t }\left( {1-\frac{1.7z_g }{L}\sqrt{\frac{EI_z }{GI_t }}} \right) \end{aligned}$$

(2)

$$\begin{aligned}&M_{cr} =\frac{p_{cr} L^{2}}{8}=\frac{c_1 \pi ^{2}EI_z }{L^{2}}\left[ {\sqrt{\frac{L^{2}GI_t }{\pi ^{2}EI_z }+\left( {c_2 z_g } \right) ^{2}}-c_2 z_g } \right] \nonumber \\ \end{aligned}$$

(3)

Results of parametric study

In this section, the results will be considered separately for positive loads $(\hbox {F}_{\mathrm{pos}}$ or $\hbox {p}_{\mathrm{pos}}$) and negative loads $(\hbox {F}_{\mathrm{neg}}$ and $\hbox {p}_{\mathrm{neg}}$), due to their significantly different behaviour. For each of both groups, the critical buckling loads and the corresponding buckling modes will be considered. In the figures of the buckling modes, the total displacement magnitudes are given as a contour plot, with minimum value 0 (blue) and maximum value 1 (red), as Abaqus scales all displacements in an eigenmode so that the maximum displacement is one.

Fig. 10

Effect on buckling shape of k (N/m/m) for positive point load $(\hbox {F}_{\mathrm{pos}})$ and low length L. Monolithic glass beam with h/L $=$ 1/10 and L $=$ 3 m

Fig. 11

Effect on buckling shape of k (N/m/m) for positive point load $(\hbox {F}_{\mathrm{pos}})$ and high length L. Monolithic glass beam with h/L $=$ 1/10 and L $=$ 12 m

Positive loads $F_{pos}$ and $p_{pos}$

For the positive (downward) loads, the buckling shape differs significantly, depending on the type of load and dimensions of the considered beam. For most beams loaded by a positive point load $\hbox {F}_{\mathrm{pos}}$, the buckling mode shape is similar to the one depicted in Fig 10. For increasing spring stiffness the number of half waves increases. For low spring stiffness values k, the maximum displacements are at the top edge, corresponding with the expected lateral-torsional buckling behaviour: the compressed edge moves sideward. However, as k increases, the stiffer springs will restrain the top edge, and the bottom edge will display the largest displacements. Simultaneously, the number of half waves increases and the top edge will still buckle sideways, but only at the location of the highest compressive stresses and very locally. The buckling mode will change from pure global to a global mode with distortions, in which the glass plate no longer remains straight.

Fig. 12

Effect on buckling shape of k (N/m/m) for positive line load $(\hbox {p}_{\mathrm{pos}})$ and low length L. Monolithic glass beam with h/L $=$ 1/10 and L $=$ 3 m

Fig. 13

Effect on buckling shape of k (N/m/m) for positive line load $(\hbox {p}_{\mathrm{pos}})$ and high length L. Monolithic glass beam with h/L $=$ 1/10 and L $=$ 12 m

For beams with a higher length L, the effect of the increasing spring stiffness manifests itself earlier (Fig. 11). For the highest spring stiffness values, the buckling mode will no longer be global, but local. In the parametric study, this effect was the strongest for beams with the highest lengths L and highest h/L values. For the lower h/L and L values, the buckling mode was a mixed distortional buckling mode, with both global and local deformations.

For the beams loaded by the uniform line load $\hbox {p}_{\mathrm{pos}}$, the behaviour was generally similar to that of the beams with point loads $\hbox {F}_{\mathrm{pos}}$, especially for the low k values. However, for the higher k values, it could be seen that generally more local waves were present in the beams’ mid spans (Figs. 12, 13). This can be attributed to the different bending moment distribution for a line load: compared with the bending moment distribution resulting from a point load, a slower variation of the bending moment in the mid span is present. This results in a greater area of large compressive stresses in mid span than for a point load. For the laminated beams, the observed behaviour was similar to that of the monolithic beams. Consequently, this will not be discussed separately.

For each geometry, $\Delta$load could be determined according to Eq. 4, for a point load F or line load p. In this equation, $\hbox {F}_{\mathrm{cr,k }}$ and $\hbox {p}_{\mathrm{cr,k} }$ are the eigenvalues obtained in Abaqus for the considered spring stiffness. The values $\hbox {F}_{\mathrm{cr,k\,=\,0}}$ and $\hbox {p}_{\mathrm{cr,k\,=\,0}}$ are the numerically obtained values for the eigenvalues for the same geometry, but with a zero spring stiffness. Thus, the advantageous effect of the lateral restraints is represented by $\Delta$load. Additionally, the ratio of positive and negative loads for a given beam was determined according to Eqs. 5 or 6. In Figs. 14 and 15, the resulting $\Delta$load values for point loads and the load ratio $\hbox {F}_{\mathrm{pos}}/\hbox {F}_{\mathrm{neg}}$ are depicted for monolithic beams. Similar graphs for line loads $\hbox {p}_{\mathrm{pos}}$, as well as those for laminated beams are included in the Appendix 1 (Figs. 19, 21, 22, 23, 26, 27).

$$\begin{aligned}&\Delta load=\frac{F_{cr,k} }{F_{cr,k\,=\,0} } \quad or \quad \Delta load=\frac{p_{cr,k} }{p_{cr,k\,=\,0} } \end{aligned}$$

(4)

$$\begin{aligned} {}&\frac{F_{pos} }{F_{neg} }=\frac{F_{cr,k,pos} }{F_{cr,k,neg} } \end{aligned}$$

(5)

$$\begin{aligned}&\frac{p_{pos} }{p_{neg} }=\frac{p_{cr,k,pos} }{p_{cr,k,neg} } \end{aligned}$$

(6)

Fig. 14

$\hbox {F}_{\mathrm{pos}}$: effect of spring stiffness k for different h/L, monolithic glass

Fig. 15

Load ratio $\hbox {F}_{\mathrm{pos,cr}}/\hbox {F}_{\mathrm{neg,cr} }$ for monolithic glass

Fig. 16

Effect on buckling shape of k (N/m/m) for negative point load $(\hbox {F}_{\mathrm{neg}})$ and low length L. Monolithic glass beam with h/L $=$ 1/10 and L $=$ 3m

Fig. 17

Effect on buckling shape of k (N/m/m) for negative line load $(\hbox {p}_{\mathrm{neg}})$ and low length L. Monolithic glass beam with h/L $=$ 1/25 and L $=$ 3 m

Fig. 18

$\hbox {F}_{\mathrm{neg}}$: effect of spring stiffness k for different h/L, monolithic glass

Negative loads $F_{neg}$ and $p_{neg}$

The buckling modes for the downward point loads $\hbox {F}_{\mathrm{neg}}$ all display the typical behaviour depicted in Fig. 16. For low spring stiffness values k, the buckling mode is the typical LTB mode, with a maximum displacement at the compressed bottom edge. With increasing spring stiffness, the displacement of the top edge decreases. For high k values, the buckling mode changes from a symmetric to antisymmetric shape.

For the line loads $\hbox {p}_{\mathrm{neg}}$, the observed behaviour corresponded with the behaviour shown in Fig. 17. Different to what occurs for $\hbox {F}_{\mathrm{neg}}$, the buckling mode now remains symmetric for increasing k values. For both negative loads, the buckling mode remains global: no web distortion could be observed. For the laminated beams subjected to negative points loads or line loads, the observed buckling mode shapes were similar to those for the monolithic beams.

In Fig. 18, the resulting $\Delta$load values for point loads $\hbox {F}_{\mathrm{neg}}$ are depicted for monolithic beams. The corresponding graphs for line loads, as well as those for laminated beams are included in the Appendix 1 (Figs. 20, 24, 25).

Discussion of results

Discussion of results for positive loads $F_{pos}$ and $p_{pos}$

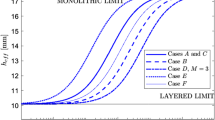
In Fig. 14, the $\Delta$load value is given for a positive point load $\hbox {F}_{\mathrm{pos}}$ working on a monolithic glass beam. As expected, the effect of the restraint increases with increasing k values. Furthermore, $\Delta$load increases with increasing lengths L and decreasing h/L ratios: it reaches a maximum value of 176 for a length L of 12 m and h/L $=$ 1/25. For small lengths however, the effect of the restraint remains equal for all h/L ratios. The effect of k is visible from minimum stiffness values $\hbox {k}_{\mathrm{min}}$ of about $10^{2}$ N/m/m for the high lengths (L $=$ 12m), and $\hbox {k}=10^{4}$ N/m/m for the low lengths (L $=$ 3m). These values are substantially below the realistic stiffness values for structural sealant joints, which means that the sealant joints will exert a non-negligible restraining effect on the top edge of the beam when considering the critical LTB load.

For high h/L values and high lengths L, a plateau is noticeable in Fig. 14 for the higher k values for $\hbox {F}_{\mathrm{pos}}$. This plateau is due to the observed local buckling in Fig. 11. For these beams, the assumption that the cross-section remains straight is no longer valid. Thus, care should be taken that these local buckling modes are not overlooked when considering only global buckling with straight cross-sections. However, for realistic stiffness values between 3 $\times$ $10^{5}$ N/m/m and 2 $\times$ $10^{6}$ N/m/m, as given in Table 3, the beams remain outside of the zone governed by local buckling. For these stiffness values, the values of $\Delta$ load vary between 3 and 27 for $\hbox {F}_{\mathrm{pos}}$, which means that the critical load can be multiplied by a factor between 3 and 27 if the lateral restraint provided by the silicone sealant joint is taken into account. Within the realistic slenderness range, the effect on $\Delta$load of variations of h/L is much smaller than the effect of L.

The obtained $\Delta$load values are given in the Appendix in Fig. 19 for the positive line load $\hbox {p}_{\mathrm{pos}}$ working on a monolithic beam. The effect of lateral springs is slightly higher for $\hbox {p}_{\mathrm{pos}}$ than for $\hbox {F}_{\mathrm{pos}}$, but overall similar conclusions can be drawn for the line load as for the point load. The values of $\Delta$load vary between 4 and 30 for the earlier cited realistic stiffness values.

Bedon and Amadio (2015a) also studied the strengthening effect of structural sealant joints on the critical buckling load for a central point load on a beam with a restrained top edge, subjected to top and bottom edge loads. The results obtained by Bedon and Amadio for top edge line loads and central point loads can be compared with the results obtained in this study for $\hbox {F}_{\mathrm{pos}}$ and $\hbox {p}_{\mathrm{pos}}$. Bedon and Amadio have not noticed any local buckling, whereas this was an important remark for the current study. This could possibly be explained by the different range of spring stiffness values studied, which only goes up to $10^{6}$ N/m/m in Bedon and Amadio’s study. Apart from this, the general trends are confirmed. The results shown in Bedon and Amadio (2015a) are of the same magnitude for comparable cross-sections. Furthermore, the lower values of $\Delta$load for point loads compared with line loads, were corroborated. Lastly, the increase in half-wave lengths in the eigenmode shape for increasing k values was confirmed.

For the laminated beams, Figs. 22 and 23 depict the $\Delta$load values for respectively point loads $\hbox {F}_{\mathrm{pos}}$ and line loads $\hbox {p}_{\mathrm{pos}}$. Overall similar trends are noticeable, but the obtained $\Delta$load values are considerably smaller for the laminated beams than for the monolithic beam, which is probably due to the modified geometry and the accompanying changes in cross-sectional properties of the cross-section: the effective thicknesses of the laminated beams are higher (Fig. 6) than the thickness of the monolithic beams. For both positive loads, it can be seen that the horizontal plateaus for high k values are reached for lower lengths than for the monolithic beams. For the realistic range of stiffness values k (3 $\times$ $10^{5 }- 2\times$ $10^{6}$ $\hbox {N/m}^{2})$, the restraint amplification factors $\Delta$load vary between 2 and 12 for the point loads $\hbox {F}_{\mathrm{pos}}$ and between 3 and 13 for the line load $\hbox {p}_{\mathrm{pos}}$.

Discussion of results for negative critical loads $F_{neg}$ and $p_{neg}$

The critical loads for $\hbox {F}_{\mathrm{neg}}$ are depicted in Fig. 18 for monolithic beams. As expected, the advantageous critical load amplification factor $\Delta$load is considerably smaller for all negative loads than for the positive loads. The value of $\Delta$load increases with increasing k; k will have more influence for increasing lengths L and decreasing h/L ratios or heights h. A horizontal plateau is noticeable for almost all h/L and L values, and is most noticeable for a high L value and high h/L value. The corresponding buckling mode shape is always a global buckling mode shape without web distortion, but will change from symmetric to antisymmetric for the higher k values, as depicted in Fig. 16. For the range of realistic stiffness values k ($3 \times 10^{5 }$ to 2 $\times$ $10^{6} \hbox {N/m}^{2})$, the value of $\Delta$load varies between 2 and 8. Here, the effect of h/L on the $\Delta$load value cannot be neglected. The effect of k is visible from minimum stiffness values $\hbox {k}_{\mathrm{min}}$ of about $10^{2}$ N/m/m for the high lengths, and $\hbox {k}= 10^{4} \hbox {N/m/m}$ for the low lengths, which corresponds with the values obtained for positive loads.

All other graphs are included in the Appendix 1. In Fig. 20, the effect of the stiffness k for a negative line load $\hbox {p}_{\mathrm{neg}}$ is depicted. The overall effect on $\Delta$load is similar as for $\hbox {F}_{\mathrm{neg}}$, but the obtained values are slightly higher. For the range of realistic stiffness values k, the value of $\Delta$load varies between 3 and 9.

For the laminated beams, similar observations can be made as for the monolithic beams, taking into account that the values of $\Delta$load are smaller and that the horizontal plateau for high k values has not yet been reached for all considered geometries (Figs. 24, 25). For the range of realistic stiffness values k, the value of $\Delta$load varies between 2 and 5 for both $\hbox {F}_{\mathrm{neg}}$ and $\hbox {p}_{\mathrm{neg}}$.

The plateau length is much longer for the negative loads than for the positive loads, and even enters the range of realistic k values for L $=$ 12 m and h/L $=$ 1/10. For these geometries, it would not be useful to further increase the stiffness of the sealant joint beyond the value for which the plateau is reached, if only the critical load for negative loads was considered.

Ratio of positive and negative critical loads

The ratio between the positive and negative loads is given in Fig. 15, for monolithic beams with a point load F. For monolithic beams with a line load, this ratio is depicted in Fig. 21 in the Appendix 1. The values for the laminated beams are in the Appendix 1 as well, in Figs. 26 and 27. The ratios are higher for line loads than for point loads, and higher for the considered monolithic beams than for the considered laminated beams.

If k $\approx$ 0, it is expected that the $\hbox {F}_{\mathrm{pos,cr}}$ is smaller than $\hbox {F}_{\mathrm{neg,cr}}$ and likewise for the line load p. This is caused by the more detrimental position of the load introduction relative to the shear centre for positive loads than for negative loads. However, it can be seen that this effect disappears once a considerable lateral restraint at the top of the beam is introduced. From values of k starting between 1 $\times$ $10^{4 }\hbox {N/m/m}$ and 1 $\times$ $\hbox {10}^{5} \hbox {N/m/m}$, the critical positive load will become larger than the critical negative load. This will occur earlier for line loads than for point loads, and later for shorter beam lengths.

The effect of restraining the compressed side of the beam for positive loads is considerably more advantageous than restraining the side of the beam in tension. The ratios $\hbox {F}_{\mathrm{pos}}/\hbox {F}_{\mathrm{neg}}$ and $\hbox {p}_{\mathrm{pos}}/\hbox {p}_{\mathrm{neg}}$ generally keep increasing with increasing k, because the critical negative loads reach a certain plateau, while the positive loads keep increasing with increasing k. However, for geometries with low L and high h/L, the ratio will also reach a certain plateau, due to the local buckling that occurs for these geometries, already mentioned earlier. It is expected that local buckling will occur for all geometries once the stiffness is high enough, but the corresponding stiffness values will lie far beyond the range of realistic stiffness values.

Conclusions and further research

In the current investigation, the restraining effect of structural sealant joints on the critical LTB load was investigated for one typical monolithic and one typical laminated cross-section, in a large numerical parametric study. Four load cases were considered for a beam with a continuous spring restraint along its top edge: a downward central point load $\hbox {F}_{\mathrm{pos}}$, a downward line load $\hbox {p}_{\mathrm{pos}}$, an upward point load $\hbox {F}_{\mathrm{neg}}$ and an upward line load $\hbox {p}_{\mathrm{neg}}$. All loads were applied on the top edge. A wide array of lengths L and height to length ratios h/L was considered. The stiffness of the springs representing the joints could vary between almost zero and very large values, encompassing previously determined realistic stiffness values of often used joint materials (DC 895 and SG-500).

For all considered cases, the amplification factor representing the increase in stiffness due to the presence of the restraints could be determined. For all load cases, the increase in critical load was significant, although it was higher for line loads than for point loads, and for the considered monolithic geometry than for the laminated geometry. The latter is expected to be caused by the different relative cross-sectional properties and dimensions of the two geometries.

For the positive loads, an amplification factor of the critical buckling load between 2 and 30 was obtained for the considered geometries and realistic joint stiffness values. For some geometries, local buckling or a mix of local and global buckling occurred for the higher stiffness values.

For the negative loads, a realistic amplification factor of the critical buckling load varied between 2 and 9. As expected, the advantageous effect of restraining the part of the beam in tension is much lower than the effect obtained for positive loads. All considered beams buckled in a global mode, without any deformations of the cross-section.

No large differences in behaviour between laminated and monolithic glass beams were observed. This makes it likely that equivalent or effective thickness concepts such as those in Haldimann et al. (2008) and (CEN 2013) could be used to determine the critical load. However, at this point it is not certain whether the expression for the equivalent thickness would be similar as the expression used for laterally unrestrained beams.

In a next step, this investigation should be extended to cover more cross-sectional geometries with other dimensions and more layers. The effect of varying stiffness properties of the interlayer should be considered as well. If the effect of the local buckling modes is discovered to be important, a more specific study of global and local buckling modes, as well as their interaction could be set up, using General Beam theory as explained by Schafer and Ádáany (2005).

In a further step, the buckling resistance should be determined as well, taking into account geometric imperfections, geometric nonlinear behaviour, the fracture strength of glass and the strength of the joint. Ideally, the numerical models used to obtain this buckling resistance would be validated by experiments on beams with a laterally restrained edge. An important issue here is which imperfection shape should be considered: the imperfection should ideally correspond with the most detrimental realistic imperfection shape. This detrimental imperfection shape is expected to have at least a torsional component, as observed in the eigenmodes. However, current information about realistic imperfection shapes is very limited: Belis et al. (2011) measured the lateral imperfection shape, but information about torsional imperfections is completely lacking.

Appendices

Appendix 1: Further results

Results for 1L (monolithic glass)

See Figs. 19, 20 and 21.

Results for 2L (laminated glass)

See Figs. 22, 23, 24, 25, 26 and 27.

Fig. 19

$\hbox {p}_{\mathrm{pos}}$: effect of spring stiffness k for different h/L, monolithic glass

Fig. 20

$\hbox {p}_{\mathrm{neg}}$: effect of spring stiffness k for different h/L, monolithic glass

Fig. 21

Load ratio $\hbox {p}_{\mathrm{pos,cr}}/\hbox {p}_{\mathrm{neg,cr} }$ for monolithic glass

Fig. 22

$\hbox {F}_{\mathrm{pos}}$: effect of spring stiffness k for different h/L, laminated glass

Fig. 23

$\hbox {p}_{\mathrm{pos}}$: effect of spring stiffness k for different h/L, laminated glass

Fig. 24

$\hbox {F}_{\mathrm{neg}}$: effect of spring stiffness k for different h/L, laminated glass

Fig. 25

$\hbox {p}_{\mathrm{neg}}$: effect of spring stiffness k for different h/L, laminated glass

Fig. 26

Load ratio $\hbox {F}_{\mathrm{pos,cr}}/\hbox {F}_{\mathrm{neg,cr} }$ for laminated glass

Fig. 27

Load ratio $\hbox {p}_{\mathrm{pos,cr}}/\hbox {p}_{\mathrm{neg,cr} }$ for laminated glass

Appendix 2: Equivalent cross-sectional properties for laminated beams 2L

The expressions for the equivalent cross-sectional properties in this appendix are valid for laminated beams consisting out of two identical glass panes and one interlayer, subjected to lateral-torsional buckling. The derivation of the expressions is based on the sandwich theory, as described by Luible (2004). These expressions are also given in Haldimann et al. (2008). The corresponding dimensions are given in Fig. 5. In these expressions, E and $\hbox {E}_{\mathrm{i}}$ are the moduli of elasticity of respectively the glass and the interlayer, while G and $\hbox {G}_{\mathrm{i}}$ are the shear moduli of respectively the glass and the interlayer. Only simply supported beams with fork supports are considered, corresponding with the scope described in Sect. 3.1.

The equivalent weak-axis bending stiffness $\hbox {EI}_{\mathrm{eff}}$ is given by Eq. 7. This expression is valid for all lateral-torsional buckling problems corresponding with a uniform bending moment sign along the beam. The values of the parameters $\hbox {I}_{\mathrm{s}}$, $\upalpha$ and $\upbeta$ can be determined using Eqs. 8–10.

$$\begin{aligned}&EI_{z,eff} =EI_s \left( {\frac{\alpha \beta \pi ^{2}+\alpha +1}{1+\pi ^{2}\beta }} \right) \end{aligned}$$

(7)

$$\begin{aligned}&I_s =2ht\left( {\frac{t_i +t}{2}} \right) ^{2} \end{aligned}$$

(8)

$$\begin{aligned}&\alpha =\frac{ht^{3}}{6I_s } \end{aligned}$$

(9)

$$\begin{aligned}&\beta =\frac{t_i }{G_i h\left( {t+t_i } \right) ^{2}}\frac{EI_s }{L^{2}} \end{aligned}$$

(10)

The equivalent torsional stiffness $\hbox {GI}_{\mathrm{t,eff} }$ (Eq. 11) is composed of the contribution of each glass pane GI (Eq. 12) and an additional term $\hbox {GI}_{\mathrm{t,comp}}$ caused by the composite action (Eq. 13). The values of $\uplambda _{\mathrm{LT}}$ and $\hbox {I}_{\mathrm{s,t} }$ are determined by Eqs. 14 and 15.

$$\begin{aligned}&GI_{\textit{t,eff}} =GI_t +GI_t +GI_{\textit{t,comp}} \end{aligned}$$

(11)

$$\begin{aligned}&GI_t =G\frac{ht^{3}}{3} \end{aligned}$$

(12)

$$\begin{aligned}&GI_{\textit{t,comp}} =GI_{s,t} \left( {1-\frac{\tanh \left( {0.5\lambda _{LT} h} \right) }{0.5\lambda _{LT} h}} \right) \end{aligned}$$

(13)

$$\begin{aligned}&\lambda _{LT} =\sqrt{\frac{G_i }{G}\frac{2}{t\cdot t_i }} \end{aligned}$$

(14)

$$\begin{aligned}&I_{s,t} =2ht\left( {t+t_i } \right) ^{2} \end{aligned}$$

(15)

Based on the equivalent bending stiffness $\hbox {EI}_{\mathrm{z,eff}}$, the equivalent thickness $(\hbox {t}_{\mathrm{eff,EIz}})$ for the bending stiffness calculation for an equivalent monolithic glass beam can be determined (Eq. 16). Similarly, the equivalent thickness $(\hbox {t}_{\mathrm{eff,GIt}})$ for the torsional stiffness calculation can be determined based on $\hbox {GI}_{\mathrm{t,eff}}$ using Eq. 17.

$$\begin{aligned} t_{eff,EI_z }= & {} \root 3 \of {\frac{12EI_{\textit{z,eff}} }{Eh}} \end{aligned}$$

(16)

$$\begin{aligned} t_{eff,EI_z }= & {} \root 3 \of {\frac{3GI_{\textit{t,eff}} }{Gh}} \end{aligned}$$

(17)