1 Introduction

Ultrasound is an important imaging modality for breast screening due to several advantages. For example, it is noninvasive, free of ionizing radiation, and can be performed in real time. In addition, it has good contrast compared to mammograms in dense breast [1,2,3,4,5,6]. Clinically, three hand-held scanning approaches are commonly used: linear (also called raster), radial, and anti-radial scanning [7]. The linear scan is the most common way to obtain the sagittal and transverse planes of the breast. Nonetheless, the cross-sectional plane of the mammary duct, which is clinically important, is also important and should be obtained by using anti-radial scanning [7,8,9,10].

Since whole breast ultrasound screening is performed manually by radiologists and sonographers, the obtained results are highly dependent on the experience of the operators. To reduce the influence of human factors in ultrasound examinations, robot-assisted systems have been designed [11,12,13,14]. Automated breast ultrasound screening (ABUS) and automated whole breast ultrasound (AWBU) [15] are robotic medical systems that are specified designed for breast screening. Based on the system designs, breast ultrasound can be performed either semiautomatically or guided by a moving structure. On contrast to ABUS and AWBU, the iVu system [16] was developed for breast screening using radial scanning. Despite the importance of fitting the body shape, none of the existing systems focus on an adaptive scan path: a predetermined curved scan pattern is chosen by ABUS and iVu, and the orientation of the transducer in AWBU is handled and guided by the operator. The functionality of the available commercialized systems for breast screening is limited by these predetermined scan trajectories.

1.1 Goals of This Study

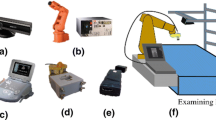
To the best of our knowledge, only linear and radial scanning products are available commercially. Here we propose an ultrasound scanning system to achieve anti-radial scanning for whole breast screening. Previously we have developed a conformal ultrasound scanning system for linear scanning only. The system setup is shown in Fig. 1, and details about the operation of the developed system are available elsewhere [17]. In brief, the system enables the generation of a scanning path for each individual examinee based on the spatial information sensed by a 3D camera, and a robotic arm with six degrees of freedom is used to perform conformal whole breast scanning. A customized transducer holder was designed for connecting the robotic arm and the ultrasound transducer of a portable ultrasound scanning system. The present study focused on achieving anti-radial breast scanning by (1) modifying the existing algorithms and (2) improving the design of the transducer holder. In addition, we generated the corresponding 3D volume data for each individual scan.

Fig. 1
figure 1

The developed automatic conformal ultrasound scanning system for whole breast screening

Full size image

2 Materials and Methods

A newly designed transducer holder was introduced, and the surface reconstruction and scan-path-smoothing algorithms were proposed for better approximating the target surface and to improve the scan stability, respectively. The new system allows the 3D volume of the scanned ultrasound images to be generated. The system performance was evaluated both using simulations and by scanning a breast phantom.

2.1 Rotatable Transducer Holder for Anti-radial Scanning

The transducer holder designed in the previous study could only perform linear scanning, and using the existing setup for other types of scan would damage the instruments, such as bending the wires of the transducer. Here we propose a modified rotatable transducer holder design consisting of a stepping motor (Faulhaber, Schönaich, Germany), aluminum supports, a rotating structure, and connector made by a 3D printer, as shown in Fig. 2. The operating orientation of the transducer is maintained by the rotating structure and the stepping motor. The resolution of the stepping motor is 1.8°, which is sufficient to match the system’s design criteria. Movement of the rotating structure is handled by a bearing (THK, Tokyo, Japan) with an inner radius of 80 mm. Cooperation between the stepping motor and rotating structure allows the scanning transducer to rotate ± 90°.

Fig. 2
figure 2

The modified transducer holder for anti-radial scanning

Full size image

2.2 Breast Phantom

A breast phantom (CIRS Model 052A, Norfolk, VA, US) designed to mimic the shape of the breast and the properties of amorphous lesions was used to evaluate the performance of the proposed system both using simulations and by scanning a breast phantom.

2.3 Algorithms

In our previous work we employed temporal median/mean filters to reduce the noise level of the 3D camera. The corresponding normal vector (estimated by principal-components analysis) and linear scan path (based on the desired conditions) were generated based on the detected surface. However, the effects of noise could not be effectively reduced, and the estimated normal vector exhibited a standard deviation of ~ 1.8° to 6.4°, which resulted in unnecessary movement of the robotic arm during scanning.

Algorithm development in the present study focused on (1) improving the scanning stability by using a better surface smoothing/approximation method, (2) generating the anti-radial scan path adapted to the target surface, and (3) visualizing the scan result with 3D volume data.

3 Spatial Data Smoothing for Target Surface Reconstruction

This study employed a combination of two smoothing methods (a bilateral filter and 2D B-spline) for mitigating the spatial error of the 3D camera [18]. Generally, a bilateral filter is a modified Gaussian filter that uses the difference in distance and pixel intensity as weights. In our approach, the pixel intensity represents the distance measured by the 3D camera, and the bilateral filter can be expressed by

$$I_{s} (x,y) = \frac{{\sum\limits_{i = - w/2}^{w/2} {\sum\limits_{j = - w/2}^{w/2} {G_{s} (i,j) \cdot G_{i} (i,j) \cdot I(x + i,y + j)} } }}{{\sum\limits_{i = - w/2}^{w/2} {\sum\limits_{j = - w/2}^{w/2} {G_{s} (i,j) \cdot G_{i} (i,j)} } }}$$
(1)
$$G_{s} (i,j) = e^{{ - \frac{{i^{2} + j^{2} }}{{2\sigma_{s}^{2} }}}}$$
(2)
$$G_{i} (i,j) = e^{{ - \frac{{(I(x,y) - I(x + i,y + j))^{2} }}{{2\sigma_{i}^{2} }}}}$$
(3)

where w is the window size, I and Is represent the distances of the measured and processed values, respectively, and Gs and Gi are Gaussian weightings, which can be calculated by the Gaussian distribution with standard deviations σs and σi, respectively. A B-spline is a curve-smoothing algorithm that can be modeled by the Knot vector (V), controls (P), and kth-order basis functions. The Knot vector is a sequential set of values from 0 to the number of outputs:

$$V = \left\{ {0, \cdots ,v, \cdots ,v_{\hbox{max} } } \right\}.$$
(4)

The kth order basis function, Ni,k, can be defined recursively:

$$N_{i,k} (v) = \frac{{v - v_{i} }}{{v_{i + k - 1} - v_{i} }}N_{i,k - 1} (v) + \frac{{v_{i + k} - v}}{{v_{i + k} - v_{i + 1} }}N_{i + 1,k - 1} (v)$$
(5)
$$N_{i,0} (v) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {1,} \\ {0,} \\ \end{array} } & \begin{aligned} {\text{if }}v_{i} < v < v_{i + 1} \hfill \\ {\text{otherwise}} \hfill \\ \end{aligned} \\ \end{array} } \right..$$
(6)

The B-spline curve and kth-order basis function can be defined as follows:

$$P(v) = \sum\limits_{i = 0}^{n} {P_{i} N_{i,k} (v) , { }0 < v < v_{\hbox{max} } }$$
(7)

The 2D B-spline (B-spline surface) can be defined with parameters (u, v) with n + 1 and m + 1 control points as follows:

$$P(u,v) = \sum\limits_{j = 0}^{m} {\sum\limits_{i = 0}^{n} {P_{i,j} N_{i,k} (v)M_{j,k} (u)} }$$
(8)

In this study we used a bilateral filter to address the noise issue, and a 2D B-spline was used to estimate the pixel values that could not be precisely detected.

4 Principal Component Analysis for Normal-Vector Estimation

The ultrasound transducer should remain perpendicular to the target surface during automatic scanning. This study used principle-components analysis to estimate the normal vectors of the surface. With the target coordinate (Ptarget = [xtarget, ytarget, ztarget]) on the surface, the corresponding normal vector can be derived based on the surrounding coordinates (Pi = [xi, yi, zi]). The n × 3 matrix, PCA, can be obtained by subtracting Ptarget from Pi- as shown below:

$${\text{ PCA}} = \left[ {\begin{array}{*{20}c} {{\text{P}}_{ 1} - {\text{P}}_{\text{target}} } \\ {{\text{P}}_{ 2} - {\text{P}}_{\text{target}} } \\ \vdots \\ {{\text{P}}_{\text{n}} - {\text{P}}_{\text{target}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{x}}_{ 1} - {\text{x}}_{\text{target}} } & {{\text{y}}_{ 1} - {\text{y}}_{\text{target}} } & {{\text{z}}_{ 1} - {\text{z}}_{\text{target}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\text{x}}_{ 2} - {\text{x}}_{\text{target}} } & {{\text{y}}_{ 2} - {\text{y}}_{\text{target}} } & {{\text{z}}_{ 2} - {\text{z}}_{\text{target}} } \\ \end{array} } \\ \vdots \\ {\begin{array}{*{20}c} {{\text{x}}_{\text{n}} - {\text{x}}_{\text{target}} } & {{\text{y}}_{\text{n}} - {\text{y}}_{\text{target}} } & {{\text{z}}_{\text{n}} - {\text{z}}_{\text{target}} } \\ \end{array} } \\ \end{array} } \right]$$
(9)

Then, square matrix M can be derived as

$${\text{M}} = ( {\text{PCA)}}^{\text{T}} \, \cdot {\text{PCA}} .$$
(10)

After computing the eigenvalues and eigenvectors of M, the first two eigenvectors can be used to span the target surface, and the corresponding normal vector can be generated by the cross product of the two eigenvectors. Figure 3 illustrates the relationships between the target coordinate, the surrounding coordinates, and the eigenvalues and eigenvectors.

Fig. 3
figure 3

Illustration of principle-components analysis for normal-vector estimation

Full size image

5 Generation of the Anti-radial Scan Path

The desired scanning region was selected manually before processing, and then the center of the selected scanning region could be obtained. The anti-radial scan begins in the horizontal direction. The orientation of each following scan is increased by an angle offset, θ. The contact angles, based on the reconstructed surface, were obtained by principle-components analysis. The development of the anti-radial scan path is shown in Fig. 4. In an anti-radial scan, moving across the cross-center can minimize the total scan time and the overall required movement.

Fig. 4
figure 4

The scan pattern for generating an anti-radial scan

Full size image

6 Model-Based Scan-Path Smoothing

To further improve the smoothness of the variance of the normal vectors on the scan path, we propose evaluating the normal vectors using the component ratio defined as

$$\left. {{\text{ratio}}_{\text{i}} = \frac{{{\text{nv}}_{\text{i}} }}{{{\text{norm}}\left( {\text{nv}} \right)}}} \right|_{i = x,y,z}$$
(11)

where nv denotes the normal vector [vx, vy, vz], nvi represents the x, y, and z components of nv, and the norm operation is \(\sqrt {v_{x}^{2} + v_{x}^{2} + v_{x}^{2} }\). A spherical surface was used to simulate the breast geometry. In addition, a straight path and the corresponding normal vectors represent the scan trajectory and the contact angle (Fig. 5a). The x, y, and z component ratios on the straight line are plotted in Fig. 5b, which indicates that both the x and y component ratios can be approximated by linear equations, and the z component can be approximated by a quadratic equation.

Fig. 5
figure 5

a The ideal spherical surface and the corresponding normal vector. b Ratios of the x, y, and z components

Full size image

We used the least-squares error (LSE) to approximate both the linear and quadratic equations. As shown in Fig. 5b, the ratio components of x and y can be approximated by linear equations:

$$y = mx + c$$
(12)

The error of each measured coordinate and error summation can be denoted as

$$E = \sum\limits_{i} {\left( {y_{i} - y} \right){}^{2}} \, = \sum\limits_{i} {\left( {y_{i} - mx - c)} \right){}^{2}}$$
(13)

To minimize the total error, partial differentiation is performed with respect to m and c:

$$\frac{\partial E}{\partial m} = 0 \Rightarrow m\sum\limits_{i} {x_{i}^{2} } + c\sum\limits_{i} {x_{i} } = \sum\limits_{i} {x_{i} y_{i} }$$
(14)
$$\frac{\partial E}{\partial c} = 0 \Rightarrow m\sum\limits_{i} {x_{i} } + cn = \sum\limits_{i} {y_{i} }$$
(15)

and m and c can be solved through a matrix operation:

$${\text{A}} \cdot \left[ {\begin{array}{*{20}c} {\text{m}} \\ {\text{c}} \\ \end{array} } \right] = {\text{B }} \Rightarrow \, \left[ {\begin{array}{*{20}c} {\text{m}} \\ {\text{c}} \\ \end{array} } \right] = {\text{ B / A}}$$
(16)

where the components of A and B can be obtained by

$${\text{A}} = \left[ {\begin{array}{*{20}c} {\sum\limits_{i} {x_{i}^{2} } } & {\sum\limits_{i} {x_{i} } } \\ {\sum\limits_{i} {x_{i} } } & n \\ \end{array} } \right]$$
(17)
$${\text{B }} = \left[ {\begin{array}{*{20}c} {\sum\limits_{i} {x_{i} y_{i} } } \\ {\sum\limits_{i} {y_{i} } } \\ \end{array} } \right].$$
(18)

Then the values of m and c in Eq. 12 can be obtained using the following equation; in other words, the two curves (x and y) in Fig. 5b can be approximated:

$$\left[ {\begin{array}{*{20}c} {\text{m}} \\ {\text{c}} \\ \end{array} } \right] = {\text{A}}^{ - 1} \cdot {\text{B}}$$
(19)

As shown in Fig. 5b, the ratio component of z can be approximated by a quadratic equation:

$$y = ax^{2} + bx + c.$$
(20)

The error of each measured coordinate and error summation can be denoted as follows:

$$E = \sum\limits_{i} {\left( {y_{i} - y} \right){}^{2}} = \sum\limits_{i} {\left( {y_{i} - ax^{2} - bx - c)} \right){}^{2}} .$$
(21)

To minimize the total error, partial differentiation is performed with respect to a, b, and c:

$$\frac{\partial E}{\partial a} = 0 \Rightarrow a\sum\limits_{i} {x_{i}^{4} } + b\sum\limits_{i} {x_{i}^{3} } + c\sum\limits_{i} {x_{i}^{2} } = \sum\limits_{i} {x_{i}^{2} y_{i}^{2} }$$
(22)
$$\frac{\partial E}{\partial b} = 0 \Rightarrow a\sum\limits_{i} {x_{i}^{3} } + b\sum\limits_{i} {x_{i}^{2} } + c\sum\limits_{i} {x_{i} } = \sum\limits_{i} {x_{i} y_{i}^{2} }$$
(23)
$$\frac{\partial E}{\partial c} = 0 \Rightarrow a\sum\limits_{i} {x_{i}^{2} } + b\sum\limits_{i} {x_{i} } + cn = \sum\limits_{i} {y_{i}^{2} }$$
(24)

and a, b, and c can be solved using a matrix operation:

$${\text{A}} \cdot \left[ {\begin{array}{*{20}c} a \\ b \\ c \\ \end{array} } \right] = {\text{B }} \Rightarrow \, \left[ {\begin{array}{*{20}c} a \\ b \\ c \\ \end{array} } \right] = {\text{ B/A}}$$
(25)

where the components of A and B can be obtained by

$${\text{A}} = \left[ {\begin{array}{*{20}c} {\sum\limits_{i} {x_{i}^{4} } } & {\sum\limits_{i} {x_{i}^{3} } } & {\sum\limits_{i} {x_{i}^{2} } } \\ {\sum\limits_{i} {x_{i}^{3} } } & {\sum\limits_{i} {x_{i}^{2} } } & {\sum\limits_{i} {x_{i} } } \\ {\sum\limits_{i} {x_{i}^{2} } } & {\sum\limits_{i} {x_{i} } } & n \\ \end{array} } \right]$$
(26)
$${\text{B }} = \left[ {\begin{array}{*{20}c} {\sum\limits_{i} {x_{i}^{2} y_{i}^{2} } } \\ {\sum\limits_{i} {x_{i} y_{i}^{2} } } \\ {\sum\limits_{i} {y_{i}^{2} } } \\ \end{array} } \right].$$
(27)

Then the values of a, b, and c in Eq. 20 can be obtained using the following equation; in other words, the z curve in Fig. 5b can be approximated:

$$\left[ {\begin{array}{*{20}c} a \\ b \\ c \\ \end{array} } \right] = {\text{A}}^{ - 1} \cdot {\text{B}} .$$
(28)

With these approximations, the normal vector described in Eq. 11 can be expressed as follows:

$$nv_{i} = \tfrac{{\left[ {\begin{array}{*{20}c} {{\text{ratio}}_{\text{x,i}} } \\ {{\text{ratio}}_{\text{y,i}} } \\ {{\text{ratio}}_{\text{z,i}} } \\ \end{array} } \right]}}{{\sqrt {{\text{ratio}}_{\text{x,i}}^{2} + {\text{ratio}}_{\text{y,i}}^{2} + {\text{ratio}}_{\text{z,i}}^{2} } }}.$$
(29)

7 3D Volume Data Reconstruction

The spatial information of each scanned ultrasound image is recorded during the conformal scan, which can be used to align the scan results. A mesh-grid volume data set is created for the reconstruction of volume data. Each pixel of the ultrasound image can be mapped onto the data expression grid, as shown in Fig. 6.

Fig. 6
figure 6

a 3D alignment of scan results. b Volume grid for 3D reconstruction. c Definition of the distance of a pixel to each corner

Full size image

The coordinate expression of each pixel can be represented as

$${\mathbf{P}}_{ 1} = \left[ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ \end{array} } \right].$$
(30)

The intensity of each pixel is determined based on its eight surrounding nodes, and the intensity of each node can be obtained using the distance weighting sum:

$${\text{Volume\_intensity (x,y,}}z )= \frac{{\sum\limits_{i} {{\text{dist}}_{\text{i}} \cdot {\text{intensity}}_{\text{i}} } }}{{\sum\limits_{i} {{\text{dist}}_{\text{i}} } }}$$
(31)
$${\text{Dist}} = {\text{norm( target - P}}_{\text{i}} { )} .$$
(32)

8 Performance Evaluation Results

8.1 Surface Reconstruction

Two ideal surfaces (flat and spherical) with added random noise were used to simulate the surfaces captured by the 3D camera. The bilateral filter was modeled by w = 3, σs = 2, and σi = 1 (as defined in Eqs. 1 to 3). The 2D B-spline had an order of 3. The processed results were compared with the ideal surfaces. The mean squared error (MSE) and standard deviation were used to evaluate the coordinate differences between the reference and filtered surfaces. There was little improvement in the MSE (up to 4%), but the standard deviations of both surfaces were reduced substanti-ally (50–80%), and so fewer adjustments were needed to the position of the transducer while scanning. The comparisons are presented in more detail in Table 1 and Fig. 7.

Table 1 MSE/standard-deviation values for different filter configurations
Full size table
Fig. 7
figure 7

Visualization of normal-vector estimation by principle-components analysis. a, b Reference surfaces. c, d Simulated surfaces detected by the 3D camera. Reconstructed surfaces after smoothing using a bilateral filter (e, f), a 2D B-spline (g, h), and a bilateral filter plus a 2D B-spline (i, j)

Full size image

8.2 Improvement in Normal-Vector Estimation

The normal vector was estimated using principle-components analysis and the cross product with the same surface conditions as mentioned above. The error in normal-vector estimation is defined by the angle difference between the reference and estimated normal vectors. Using principle-components analysis resulted in a higher accuracy and lower standard deviation than when using the cross product, with typically 35–40% improvement being achieved by processing with principle-components analysis. More details are presented in Table 2 and Fig. 7.

Table 2 MSE/standard-deviation values for the estimations of normal vectors
Full size table

8.3 Model-Based Scan-Path-Smoothing Algorithm

The spatial-data-smoothing algorithm can successfully reduce the noise level of the reconstructed surface and the corresponding normal vector (as mentioned in Sect. 8.1), but the proposed model-based scan-path-smoothing algorithm aimed to further reduce unnecessary vibration caused associated with the standard deviation or angle error. The improvement obtained by using this algorithm was verified using both the simulated surface and actual data from the breast phantom. Figure 8a and c show the original normal vectors, while Fig. 8b and d display the smoothed normal vectors; these visualizations demonstrate that the estimated normal vector can be successfully smoothed.

Fig. 8
figure 8

a, c Normal vectors with respect to the simulated and actual surfaces. b, d Results obtained by smoothing using the model-based scan-path-smoothing algorithm

Full size image

8.4 Anti-radial Scanning and 3D Volume Data Reconstruction

Anti-radial scanning with 30 angle increments and a total of 6 scan paths was performed on the breast phantom. The scanning stability was improved when scanning a circular region with a radius of 50 mm at a scan speed of 5 mm/s. A total scan time of around 3.5 min was required in the current system setup. 3D volume data were generated based on the recorded spatial data. Figure 9a shows one of the six reconstructed 3D data volumes. To further verify the reconstructed results, one section of each reconstruction was chosen and compared with the actual ultrasound image of the breast phantom in Fig. 9b–m.

Fig. 9
figure 9

a A reconstructed 3D data volume. Comparisons between the cross sections of the 3D reconstruction data (b–g) and the actual ultrasound images (h–m)

Full size image

9 Discussion

We have successfully performed anti-radial scanning, improved the scan stability, and visualized the scan results in 3D volume representations using our modified system. However, there are some limitations that cannot be overcome using with the current prototype.

9.1 Limitations of the Current System Setup for Anti-radial Scanning

An additional rotation, as allowed by the modified transducer holder, minimized the requirement for a posture change in the anti-radial scan. Nonetheless, additional 100-mm and 250-mm extensions along the x- and z-axes were unavoidable because of the complexity of the holder design. Also, the effective scan region is restricted to within a circular region with a radius of less than 50 mm.

Choosing the appropriate scanning speed is important to obtain the optimal trade-off between the spatial resolution and the posture changes of the robot arm. By scanning at 5 mm/s, a spatial resolution of 0.67 mm can be obtained, but results in a processing time of around 3.5 min. Increasing the scan speed will reduce the scan accuracy (spatial resolution) and scan stability (due to larger changes in the posture of the robot arm). For processing at a higher scan speed, an ultrasound system with a higher frame acquisition rate (e.g., 100 fps) is suggested. On the other hand, processing with a smaller transducer holder can reduce the required posture changes of the robot arm while scanning. In addition, the algorithm for determining the scan region in anti-radial scanning was not addressed in this study due to the large variation between examinees. To avoid any improper determinations, manually selecting the scan region is suggested.

9.2 Performance of the Proposed Algorithms

The accuracy of our proposed method was tested using ideal flat and spherical surfaces. The results show that the proposed algorithm can reduce the standard deviation of the estimated error and improve the smoothness of the estimated normal vector. The proposed filter configuration (bilateral filter + 2D B-spline) reduced the estimated errors by 50%, which is the key point for smoothing the reconstructed surface. Based on the smoothed reconstructed surface, the principle-components analysis method can provide the estimated normal vector with a lower angle standard deviation (reduced from 2.51° to 1.51°, as indicated in Table 2). The reconstruction results also show that the proposed system can smoothly move across the breast phantom surface without unnecessary disturbances.

9.3 Deformation of the Breast Phantom

Due to deformation of the breast phantom, differences in the geometry between the reconstructed surface and the actual images are unavoidable. This deformation issue was alleviated in our study in two ways. First, our general setup includes a contact force sensor to make sure that the ultrasound transducer establishes good contact with the skin while avoiding applying an excessive force as often seen during manual scanning. In other words, our use of a force sensor minimized the deformation. Second, the image object (i.e., breast) can be easily confined and fixed during the scanning by using a large membrane covering the entire breast. This is already used in ABUS by applying a large transducer holder and a scanning frame on the breast. A similar scanning frame can also be used in our setup to avoid the deformation problem. The data presented in Tables 1 and 2 indicate the good accuracy (submillimeter) that can be achieved with our proposed approach.

10 Conclusions

This study developed a prototype of an automatic breast ultrasound screening system for anti-radial scanning. Such an automatic system is clinically important, and this is the first report of such a system in the literature. A modified transducer holder consisting of a stepping motor and rotating structure was designed to adjust the orientation of the transducer. The surface-model spatial-data-smoothing algorithm provided a better approximation of the target surface. The standard deviation of the surface reconstruction was effectively reduced (by 50–80%) in the simulations of flat and spherical surfaces, while an improvement of 35–40% in angle accuracy was also achieved. Our model-based scan-path-smoothing algorithm further optimized the suggested contact angle based on the shape of the breast, and this was verified in breast phantom scans. Six-direction anti-radial scanning was performed within a circular region (with a radius of 50 mm) of the breast phantom, and the overall processing time was approximately 3.5 min. The 3D volume reconstruction of each scan path was obtained, and the quality of the reconstruction was verified in comparisons of actual ultrasound images obtained from the breast phantom.