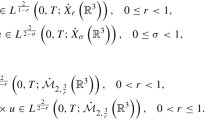Abstract
This work establishes a new logarithmical improved regularity criterion for the 3D Boussinesq equations in terms of one directional derivative of the pressure (i.e., \(\partial _{3}P\)) on framework of the anisotropic Lebesgue spaces. More precisely, it is proved that if
for some \(T>0\), then the corresponding solution \((u,\theta )\) to the 3D Boussinesq equations is regular on [0, T].
Similar content being viewed by others
References
Abidi, H., Hmidi, T.: On the global well-posedness for Boussinesq system. J. Differ. Equ. 233, 199–220 (2007)
Adams, R.: Sobolev Spaces. Academic Press, New York (1975)
Beirão da Veiga, H.: A new regularity class for the Navier–Stokes equations in \(R^n\). Chin. Ann. Math. 16, 407–412 (1995)
Beirão da Veiga, H.: On the smoothness of a class of weak solutions to the Navier–Stokes equations. J. Math. Fluid Mech. 2, 315–323 (2000)
Berselli, L., Galdi, G.: Regularity criteria involving the pressure for the weak solutions to the Navier–Stokes equations. Proc. Am. Math. Soc. 130, 3585–3595 (2002)
Cao, C., Qin, J., Titi, E.: Regularity criterion for solutions of three-dimensional turbulent channel flows. Comm. Partial Differ. Equ. 33, 419–428 (2008)
Cao, C., Titi, E.: Regularity criteria for the three-dimensional Navier–Stokes equations. Indiana Univ. Math. J. 57, 2643–2662 (2008)
Cao, C., Regmi, D., Wu, J.: The 2-D MHD equations with horizontal dissipation and horizontal magnetic diffusion. J. Differ. Equ. 254, 2661–2681 (2013)
Cao, C., Wu, J.: Two regularity criteria for the 3D MHD equations. J. Differ. Equ. 248, 2263–2274 (2010)
Cao, C., Wu, J.: Global regularity for the 2-D MHD equations with mixed partial dissipation and magnetic diffusion. Adv. Math. 226, 1803–1822 (2011)
Du, L., Zhou, D.: Global well-posedness of two-dimensional magnetohydrodynamic flows with partial dissipation and magnetic diffusion. SIAM J. Math. Anal. 47, 1562–1589 (2015)
Fan, J., Jiang, S., Nakamura, G., Zhou, Y.: Logarithmically improved regularity criteria for the Navier–Stokes and MHD equations. J. Math. Fluid Mech. 13, 557–571 (2011)
Fan, J., Malaikah, H., Monaquel, S., Nakamura, G., Zhou, Y.: Global Cauchy problem of 2D generalized MHD equations. Monatsh. Math. 175(1), 127–131 (2014)
Fan, J., Jia, X., Nakamura, G., Zhou, Y.: On well-posedness and blowup criteria for the magnetohydrodynamics with the Hall and ion-slip effects. Z. Angew. Math. Phys. 66, 1695–1706 (2015)
Gala, S.: On the regularity criterion of strong solutions to the 3D Boussinesq equations. Appl. Anal. 90, 1829–1835 (2011)
Gala, S., Ragusa, M.: Logarithmically improved regularity criterion for the Boussinesq equations in Besov spaces with negative indices. Appl. Anal. 95, 1271–1279 (2016)
Geng, J., Fan, J.: A note on regularity criterion for the 3D Boussinesq system with zero thermal conductivity. Appl. Math. Lett. 25, 63–66 (2012)
Jia, X., Zhou, Y.: A new regularity criterion for the 3D incompressible MHD equations in terms of one component of the gradient of pressure. J. Math. Anal. Appl. 396, 345–350 (2012)
Jia, X., Zhou, Y.: Regularity criteria for the 3D MHD equations involving partial components. Nonlinear Anal. Real World Appl. 13, 410–418 (2012)
Jia, X., Zhou, Y.: Ladyzhenskaya–Prodi–Serrin type regularity criteria for the 3D incompressible MHD equations in terms of \(3\times 3\) mixture matrices. Nonlinearity 28, 3289–3307 (2015)
Jia, Y., Zhang, X., Dong, B.: Remarks on the blow-up criterion for smooth solutions of the Boussinesq equations with zero diffusion. Commun. Pure Appl. Anal. 12, 923–937 (2013)
Jiang, Z., Wang, Y., Zhou, Y.: On regularity criteria for the 2D generalized MHD system. J. Math. Fluid Mech. 18, 331–341 (2016)
Liu, Q., Dai, G.: On the 3D Navier–Stokes equations with regularity in pressure. J. Math. Anal. Appl. 458, 497–507 (2018)
Majda, A.: Introduction to PDEs and Waves for the Atmosphere and Ocean. Courant Lecture Notes in Mathematic, vol. 9. American Math. Soc, Providence (2003)
Mechdene, M., Gala, S., Guo, Z., Ragusa, A.: Logarithmical regularity criterion of the three-dimensional Boussinesq equations in terms of the press. Z. Angew. Math. Phys. 444, 1752–1758 (2016)
Qian, C.: A generalized regularity criterion for 3D Naiver–Stokes equations in terms of one velocity component. J. Differ. Equ. 260, 3477–3494 (2016)
Qiu, H., Du, Y., Yao, Z.: Serrin-type blow-up criteria for 3D Boussinesq equations. Appl. Anal. 89, 1603–1613 (2010)
Qiu, H., Du, Y., Yao, Z.: Blow-up criteria for 3D Boussinesq equations in the multiplier space. Commun. Nonlinear Sci. Numer. Simul. 16, 1820–1824 (2011)
Seregin, G., Šverák, V.: Navier–Stokes equations with lower bounds on the pressure. Arch. Ration. Mech. Anal. 163, 65–86 (2002)
Xu, F., Zhang, Q., Zheng, X.: Regularity criteria of the 3D Boussinesq equations in the Morrey-Campanato Space. Acta Appl. Math. 121, 231–240 (2012)
Ye, Z.: A regularity criterion for the 2D MHD and viscoelastic fluid equations. Ann. Polon. Math. 114, 123–131 (2015)
Zhang, Z.: A logarithmically improved regularity criterion for the 3D Boussinesq equations via the pressure. Acta Appl. Math. 131, 213–219 (2014)
Zhang, Z.: A remark on the regularity criterion for the 3D Boussinesq equations involving the pressure gradient. Abstract Appl. Anal. 2014. Article ID 510924 (2014)
Zhang, Z.: Global regularity criteria for the n-dimensional Boussinesq equations with fractional dissipation. Electron. J. Differ. Equ. 2016, 1–5 (2016)
Zhang, Z.: An improved regularity criterion for the Navier–Stokes equations in terms of one directional derivative of the velocity field. Bull. Math. Sci. 8, 33–47 (2018)
Zhang, Z., Li, P., Yu, G.: Regularity criteria for the 3D MHD equations via one directional derivative of the pressure. J. Math. Anal. Appl. 401, 66–71 (2013)
Zhou, Y.: Remarks on regularities for the 3D MHD equations. Discrete Contin. Dyn. Syst. 12, 881–886 (2005)
Zhou, Y.: Regularity criteria for the generalized viscous MHD equations. Ann. Inst. H. Poincaré Anal. Non Linéaire 24, 491–505 (2007)
Zhou, Y., Fan, J.: A regularity criterion for the 2D MHD system with zero magnetic diffusivity. J. Math. Anal. Appl. 378, 169–172 (2011)
Zhou, Y., Fan, J.: Logarithmically improved regularity criteria for the 3D viscous MHD equations. Forum Math. 24, 691–708 (2012)
Zhou, Y., Gala, S.: A new regularity criterion for weak solutions to the viscous MHD equations in terms of the vorticity field. Nonlinear Anal. 72, 3643–3648 (2010)
Acknowledgements
The author would like to thank to his supervisor Prof. Song Jiang for many helpful comments and suggestions. He also would like to acknowledge his sincere thanks to the editor and the referees for a careful reading of the work and many valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Yong Zhou.
This work is partially supported by the National Natural Science Foundation of China (11401202).
Appendix
Appendix
This appendix provides the proof of (1.7). For the convenience of future references, we write it as a lemma.
Lemma C.1
Let \(1\le \gamma ,\alpha ,\xi ,a,t\le \infty ,1<s\le \infty \), and \(0\le \theta \le 1\). Then there exists a positive constant C such thatFootnote 1
for \(f,g,h\in C_{0}^{\infty }(\mathbb {R}^{3})\), where \(\gamma ,\alpha ,\xi ,s\) and \(\theta \) satisfying
and
Proof
The proof is essentially due to [7], and for the readers convenience, we give a simple proof. By using Hölder’s inequality, it follows that
and by using Hölder’s inequality again, one gets
By using Hölder’s and Gagliardo–Nirenberg inequalities, one obtains
where we have used (C.2), (C.3) and the following inequality
Similarly, for \(s>1\), one has
Inserting (C.5), (C.6) and (C.7) into (C.4), it follows that (C.1) holds. Thus we complete the proof of Lemma C.1. \(\square \)
Rights and permissions
About this article
Cite this article
Liu, Q. The 3D Boussinesq Equations with Regularity in One Directional Derivative of the Pressure. Bull. Malays. Math. Sci. Soc. 42, 3005–3019 (2019). https://doi.org/10.1007/s40840-018-0645-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40840-018-0645-6