Vibration and Stability Analysis of Functionally Graded Skew Plate Using Higher Order Shear Deformation Theory

Abstract

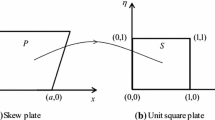
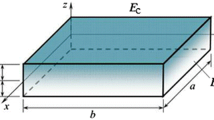
This paper deals with the vibration and buckling analysis of skew functionally graded material (FGM) plates. A finite element mathematical model is developed based on higher order shear deformation theory. The model is based on an eight noded isoparametric element with seven degrees of freedom per node. The material properties are graded along thickness direction obeying simple power-law distribution. The general displacement equation provides $\hbox {C}^{0}$ continuity. The transverse shear strain undergoes parabolic variation through the thickness of the plate. Hence, there is no requirement of a shear correction factor in this theory. The governing equation for the skew FGM plate is obtained using Hamilton’s principle. The obtained results are compared with the published results to determine the accuracy of the method. The effect of various parameters like aspect ratio, side-thickness ratio, volume fraction index, boundary conditions and skew angle on the natural frequencies and buckling loads has been investigated.

Appendix

A.1

The strain-displacement matrix [B]

$$\begin{aligned} \left[ B \right] _{1,1}= & {} N_{i,x}, \quad \left[ B \right] _{2,2} =N_{i,y}, \quad \left[ B \right] _{3,1} =N_{i,y}, \quad \left[ B \right] _{3,2} =N_{i,x}, \quad \left[ B \right] _{4,7} =N_{i,x}, \quad \left[ B \right] _{5,6} =N_{i,y},\\ \left[ B \right] _{6,6}= & {} N_{i,x}, \quad \left[ B \right] _{6,7} =N_{i,y}, \quad \left[ B \right] _{7,4} =N_{i,x}, \quad \left[ B \right] _{7,7} =N_{i,x}, \quad \left[ B \right] _{8,5} =N_{i,y} \hbox {, }\left[ B \right] _{8,6} =N_{i,y},\\ \left[ B \right] _{9,4}= & {} N_{i,y}, \quad \left[ B \right] _{9,5} =N_{i,x}, \quad \left[ B \right] _{9,6} =N_{i,x}, \quad \left[ B \right] _{9,7} =N_{i,y}, \quad \left[ B \right] _{10,3} =N_{i,x}, \quad \left[ B \right] _{10,7} =N_i,\\ \left[ B \right] _{11,3}= & {} N_{i,y}, \quad \left[ B \right] _{11,6} =N_i, \quad \left[ B \right] _{12,4} =N_i, \quad \left[ B \right] _{12,4} =N_i, \quad \left[ B \right] _{13,5} =N_i, \quad \left[ B \right] _{13,6} =N_i \end{aligned}$$

A.2

The inertia matrix [I]

$$\begin{aligned} {[I]}_{1,1}= & {} I_0, \quad [I]_{2,2} =I_0, \quad [I]_{3,3} =I_0, \quad [I]_{4,4} =c_1^2 \times I_6, \quad [I]_{4,7}\\= & {} -c_1 \times \left( {I_4 -c_1 I_6 } \right) , \\ {[I]}_{5,5}= & {} c_1^2 \times I_6, \quad [I]_{5,6} =c_1 \times \left( {I_4 -c_1 I_6 } \right) , \quad [I]_{6,5} =c_1 \times \left( {I_4 -c_1 I_6 } \right) , \\ \quad [I]_{6,6}= & {} I_2 -\,2c_1 J_4 +c_1^2 I_6, \\ {[I]}_{7,4}= & {} -c_1 \times \left( {I_4 -c_1 I_6 } \right) , \quad [I]_{7,7} =I_2 -\,2c_1 J_4 +c_1^2 I_6 \\ \hbox {where, }I_i= & {} \int \limits _{-h/2}^{h/2} {\rho z^{i}dz} \quad (i=0,2,4,6), \quad c_1 =\frac{4}{3h^{2}} \end{aligned}$$

Shape function Matrix $\left[ N \right]$

$$\begin{aligned} \left[ N \right] _{1,1} =\left[ N \right] _{2,2} =\left[ N \right] _{3,3} =\left[ N \right] _{4,4} =\left[ N \right] _{5,5} =\left[ N \right] _{6,6} =\left[ N \right] _{7,7} =N_i \end{aligned}$$

where, $N_i$ is the shape function at each node $(i=1,2,3,4,5,6,7,8)$.

A.3

$$\begin{aligned} \left[ G \right] _{1,1}= & {} N_{i,x} \quad \left[ G \right] _{2,1} =N_{i,y} \quad \left[ G \right] _{3,2} =N_{i,x} \quad \left[ G \right] _{4,2} =N_{i,y} \quad \left[ G \right] _{5,3} =N_{i,x} \quad \left[ G \right] _{6,3} =N_{i,y}\\ \left[ G \right] _{7,4}= & {} N_{i,x} \quad \left[ G \right] _{8,4} =N_{i,y} \quad \left[ G \right] _{9,5} =N_{i,x} \quad \left[ G \right] _{10.5} =N_{i,y} \quad \left[ G \right] _{11,6} =N_{i,x} \quad \left[ G \right] _{12,6} =N_{i,y}\\ \left[ G \right] _{13,7}= & {} N_{i,x} \quad \left[ G \right] _{14,7} =N_{i,y} \quad \left[ G \right] _{15,4} =N_i \quad \left[ G \right] _{16,5} =N_i \quad \left[ G \right] _{17,6} =N_i \quad \left[ G \right] _{18,7} =N_i \end{aligned}$$

The stress matrix [S]

$$\begin{aligned} \left[ S \right] _{1,1}= & {} N_x, \left[ S \right] _{1,2} =N_{xy} ; \quad \left[ S \right] _{1,7} =-c_1 P_x ; \quad \left[ S \right] _{1,8} =-c_1 P_{xy} ; \quad \left[ S \right] _{1,13}\\= & {} M_x -c_1 P_x ; \quad \left[ S \right] _{1,14} =M_{xy} -c_1 P_{xy} ; \\ \left[ S \right] _{1,15}= & {} \quad -c_2 R_x; \left[ S \right] _{1,18} =-c_1 S_{x1} ; \quad \left[ S \right] _{2,1} =N_{xy} ; \quad \left[ S \right] _{2,2} =N_y ; \quad \left[ S \right] _{2,7}\\= & {} -c_1 P_y ; \quad \left[ S \right] _{2,8} =-c_1 P_y ; \quad \\ \left[ S \right] _{2,13}= & {} M_{xy} -c_1 P_{xy} ; \quad \left[ S \right] _{2,14} =M_y -c_1 P_y ; \quad \left[ S \right] _{2,15} =-c_2 R_y ; \quad \left[ S \right] _{2,18}\\= & {} Q_y -c_2 R_y ; \quad \left[ S \right] _{3,3}=N_x ;\left[ S \right] _{3,4} =N_{xy} ; \\ \left[ S \right] _{3,9}= & {} -c_1 P_x ; \quad \left[ S \right] _{3,10} =-c_1 P_{xy} ; \quad \left[ S \right] _{3,11} =-M_x -c_1 P_x ; \quad \left[ S \right] _{3,12}\\= & {} -M_{xy} +c_1 P_{xy} ; \quad \left[ S \right] _{3,16} =-c_2 R_x ; \quad \\ \left[ S \right] _{3,17}= & {} -Q_x +c_2 R_x ; \quad \left[ S \right] _{4,3} =N_{xy} ; \quad \left[ S \right] _{4,4} =N_y ; \quad \left[ S \right] _{4,9} =-c_1 P_{xy} ; \quad \left[ S \right] _{4,10}\\= & {} -c_1 P_y ; \quad \left[ S \right] _{4,11} =-M_{xy} +c_1 P_{xy} ; \\ \left[ S \right] _{4,12}= & {} -M_y +c_1 P_y ; \quad \left[ S \right] _{4,16} =-c_2 R_y ; \quad \left[ S \right] _{4,17} =-Q_y +c_2 R_y ; \quad \left[ S \right] _{5,5}\\= & {} N_x ; \quad \left[ S \right] _{5,6}=N_{xy} ; \quad \left[ S \right] _{6,5} =N_{xy} ; \\ \left[ S \right] _{6,6}= & {} N_y ; \quad \left[ S \right] _{7,1} =-c_1 P_x ; \quad \left[ S \right] _{7,2} =-c_1 P_{xy} ; \quad \left[ S \right] _{7,7} =c_1^2 M_{x1} ; \quad \left[ S \right] _{7,8}\\= & {} c_1^2 M_{xy1} ; \quad \left[ S \right] _{7,13} =c_1^2 M_{x1} -c_1 N_{x1} ; \\ \left[ S \right] _{7,14}= & {} c_1^2 M_{xy1} -c_1 N_{xy1} ; \quad \left[ S \right] _{7,18} =-c_1 S_{x1} ; \quad \left[ S \right] _{8,1} =-c_1 P_{xy} ; \quad \left[ S \right] _{8,2}\\= & {} -c_1 P_y ; \quad \left[ S \right] _{8,7}=c_1^2 M_{xy1} ; \quad \left[ S \right] _{8,8} =c_1^2 M_{y1} ; \\ \left[ S \right] _{8,13}= & {} c_1^2 M_{xy1} -c_1 N_{xy1} ; \quad \left[ S \right] _{8,14} =c_1^2 M_{y1} -c_1 N_{y1} ; \quad \left[ S \right] _{8,18} =-c_1 S_{y1} ; \quad \left[ S \right] _{9,3}\\= & {} -c_1 P_x ; \quad \left[ S \right] _{9,4} =-c_1 P_{xy} ; \\ \left[ S \right] _{9,9}= & {} c_1^2 M_{x1} ; \quad \left[ S \right] _{9,10} =c_1^2 M_{xy1} ; \quad \left[ S \right] _{9,11} =-c_1^2 M_{x1} +c_1 N_{x1} ; \quad \left[ S \right] _{9,12}\\= & {} -c_1^2 M_{xy1} +c_1 N_{xy1} ; \quad \left[ S \right] _{9,17} =c_1 S_{x1} ; \\ \left[ S \right] _{10,3}= & {} -c_1 P_{xy} ; \quad \left[ S \right] _{10,4} =-c_1 P_y ; \quad \left[ S \right] _{10,9} =c_1^2 M_{xy1} ; \quad \left[ S \right] _{10,10}\\= & {} c_1^2 M_{y1} ; \quad \left[ S \right] _{10,11}=-c_1^2 M_{xy1} +c_1 N_{xy1} ; \\ \left[ S \right] _{10,12}= & {} -c_1^2 M_{y1} +c_1 N_{y1} ; \quad \left[ S \right] _{10,17} =c_1 S_{y1} ; \quad \left[ S \right] _{11,3}\\= & {} -M_x -c_1 P_x ; \quad \left[ S \right] _{11,4} =M_{xy} -c_1 P_{xy} ; \\ \left[ S \right] _{11,9}= & {} -c_1^2 M_{x1} +c_1 N_{x1} ; \quad \left[ S \right] _{11,10} =-c_1^2 M_{xy1} +c_1 N_{xy1} ; \quad \left[ S \right] _{11,11}\\= & {} L_x +c_1^2 M_{x1} -\,2c_1 N_{x1} ; \\ \left[ S \right] _{11,12}= & {} L_{xy} +c_1^2 M_{xy1} -\,2c_1 N_{xy1} ; \quad \left[ S \right] _{11,16}\\= & {} c_2 S_{x1} ; \quad \left[ S \right] _{12,3} =-M_{xy} +c_1 P_{xy} ; \\ \left[ S \right] _{12,4}= & {} -M_y +c_1 P_y ; \quad \left[ S \right] _{12,9} =-S_{7,14} =-c_1^2 M_{xy1} +c_1 N_{xy1} ; \quad \left[ S \right] _{12,10}\\= & {} -c_1^2 M_{y1} +c_1 N_{y1} ; \\ \left[ S \right] _{12,11}= & {} L_{xy} +c_1^2 M_{xy1} -\,2c_1 N_{xy1} ; \quad \left[ S \right] _{12,12} =L_y +c_1^2 M_{y1} -\,2c_1 N_{y1} ; \quad \left[ S \right] _{12,16}\\= & {} -c_2 S_{y1} ; \\ \left[ S \right] _{13,1}= & {} M_x -c_1 P_x ; \quad \left[ S \right] _{13,2} =M_{xy} -c_1 P_{xy} ; \quad \left[ S \right] _{13,7}\\= & {} c_1^2 M_{x1} -c_1 N_{x1} ; \quad \left[ S \right] _{13,8} =c_1^2 M_{xy1} -c_1 N_{xy1} ; \\ \left[ S \right] _{13,13}= & {} L_x +c_1^2 M_{x1} -\,2c_1 N_{x1} ; \quad \left[ S \right] _{13,14}\\= & {} L_{xy} +c_1^2 M_{xy1} -\,2c_1 N_{xy1} ; \quad \left[ S \right] _{13,15} =c_2 S_{x1} ; \\ \left[ S \right] _{13,18}= & {} S_x -c_1 S_{x1} -c_2 S_{x1} ; \quad \left[ S \right] _{14,1} =M_{xy} -c_1 P_{xy} ; \quad \left[ S \right] _{14,2}\\= & {} M_y -c_1 P_y ; \quad \left[ S \right] _{14,7} =c_1^2 M_{xy1} -c_1 N_{xy1} ; \\ \left[ S \right] _{14,8}= & {} S_{8,14} ; \quad \left[ S \right] _{14,13} =L_{xy} +c_1^2 M_{xy1} -\,2c_1 N_{xy1} ; \quad \left[ S \right] _{14,14}\\= & {} L_y +c_1^2 M_{y1} -\,2c_1 N_{y1} ; \quad \left[ S \right] _{14,15} =-c_2 S_{y1} ; \\ \left[ S \right] _{14,18}= & {} S_y -c_1 S_{y1} -c_2 S_{y1} ; \quad \left[ S \right] _{15,1} =-c_2 R_x ; \quad \left[ S \right] _{15,2} =-c_2 R_y ; \quad \left[ S \right] _{15,13}\\= & {} c_2 S_{x1} ; \quad \left[ S \right] _{15,14} =-c_2 S_{y1} ; \\ \left[ S \right] _{16,3}= & {} -c_2 R_x ; \quad \left[ S \right] _{16,4} =-c_2 R_y ; \quad \left[ S \right] _{16,11}\\= & {} c_2 S_{x1} ; \quad \left[ S \right] _{16,12} =-c_2 S_{y1} ; \quad \left[ S \right] _{17,3} =-Q_x +c_2 R_x ; \\ \left[ S \right] _{17,4}= & {} -Q_y +c_2 R_y ; \quad \left[ S \right] _{17,9} =c_1 S_{x1} ; \quad \left[ S \right] _{17,10}\\= & {} c_1 S_{y1} ; \quad \left[ S \right] _{17,11} =S_x -c_1 S_{x1} -c_2 S_{x1} ; \\ \left[ S \right] _{17,12}= & {} S_y -c_1 S_{y1} -c_2 S_{y1} ; \quad \left[ S \right] _{18,1} =Q_x -c_2 R_x ; \quad \left[ S \right] _{18,2}\\= & {} Q_y -c_2 R_y ; \quad \left[ S \right] _{18,7}=-c_1 S_{x1} ; \quad \left[ S \right] _{18,8} =-c_1 S_{y1} ; \\ \left[ S \right] _{18,13}= & {} S_x -c_1 S_{x1} -c_2 S_{x1} ; \quad \left[ S \right] _{18,14}\\= & {} S_y -c_1 S_{y1} -c_2 S_{y1} \end{aligned}$$

where,

$$\begin{aligned} \begin{array}{l} \left[ {{\begin{array}{cccccc} {N_x }&{} \quad {M_x }&{} \quad {L_x }&{} \quad {P_x }&{} \quad {N_{x1} }&{} \quad {M_{x1} } \\ {N_y }&{} \quad {M_y }&{} \quad {L_y }&{} \quad {P_y }&{} \quad {N_{y1} }&{} \quad {M_{y1} } \\ {N_{xy} }&{} \quad {M_{xy} }&{} \quad {L_{xy} }&{} \quad {P_{xy} }&{} \quad {N_{xy1} }&{} \quad {M_{xy1} } \\ \end{array} }} \right] =\displaystyle \int \limits _{-h/2}^{h/2} {\left\{ {{\begin{array}{l} {\sigma _x } \\ {\sigma _y } \\ {\sigma _{xy} } \\ \end{array} }} \right\} } \left[ {1,z,z^{2},z^{3},z^{4},z^{5}} \right] dz \\ \left[ {{\begin{array}{ccccc} {Q_x }&{} \quad {S_x }&{} \quad {R_x }&{} \quad {S_{x1} }&{} \quad {P_{x1} } \\ {Q_y }&{} \quad {S_y }&{} \quad {R_y }&{} \quad {S_{y1} }&{} \quad {P_{y1} } \\ \end{array} }} \right] =\displaystyle \int \limits _{-h/2}^{h/2} {\left\{ {{\begin{array}{l} {\tau _{xz} } \\ {\tau _{yz} } \\ \end{array} }} \right\} \left[ {1,z,z^{2},z^{3},z^{5}} \right] dz} \\ \end{array} \end{aligned}$$