Skip to main content

Advertisement

Springer Nature Link
Log in

A Framework for Triangular Fuzzy Random Multiple-Criteria Decision Making

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

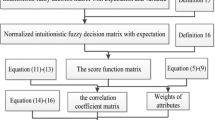
Abstract

Most real-world decisions practically occur in extremely complex environments characterized by both fuzziness and randomness. This phenomenon highlights the requirement for new evaluation methods in a fuzzy random environment and new ways to address fuzzy random multiple-criteria decision-making (MCDM) problems. This study reviews fuzzy random variable (FRV) to evaluate fuzzy random decision-making environment. Given the inaccuracy of certain precision formulas proposed in previous studies for the variance of a triangular FRV, this work presents the detailed process of calculating precision variance formulas and discusses several properties of the expectation and variance of triangular FRVs (TFRVs). The united variance of a TFRV vector is also proven to possess non-additive properties. Thus, an ordered weighted averaging (OWA) operator is extended to aggregate fuzzy random data by proposing a triangular fuzzy random OWA operator. Motivated by the idea of mean–variance analysis, an expectation-variance-based method is employed to rank TFRVs. Furthermore, a novel triangular fuzzy random MCDM method is developed, and certain numerical examples are provided to demonstrate the ability of TFRVs to comprehensively assess the performance of a specific alternative. This work also illustrates how the triangular fuzzy random MCDM framework can be extended to any fuzzy random decision-making process.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Ngan, S.C.: Correlation coefficient of linguistic variables and its applications to quantifying relations in imprecise management data. Eng. Appl. Artif. Intell. 26(1), 347–356 (2013)

    Article  Google Scholar 

  2. Wang, P., Li, S.J., Lv, Y., Chen, Z.H.: Grey qualitative modeling and control method for subjective uncertain systems. Int. J. Autom. Comput. 12(1), 70–76 (2015)

    Article  Google Scholar 

  3. Galeano, P., Wied, D.: Multiple break detection in the correlation structure of random variables. Comput. Stat. Data Anal. 76, 262–282 (2014)

    Article  MathSciNet  Google Scholar 

  4. Kwakernaak, H.: Fuzzy random variables—I. Definitions and theorems. Inf. Sci. 15(1), 1–29 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  5. Kwakernaak, H.: Fuzzy random variables—II. Algorithms and examples for the discrete case. Inf. Sci. 17(3), 253–278 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  6. Puri, M.L., Ralescu, D.A.: The concept of normality for fuzzy random variables. Ann Probab 13(4), 1373–1379 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  7. Puri, M.L., Ralescu, D.A.: Fuzzy random variables. J. Math. Anal. Appl. 114, 409–422 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  8. Kruse, R., Meyer, K.D.: Statistics with Vague Data, vol. 6. Springer, Berlin (1987)

    Book  MATH  Google Scholar 

  9. Baumol, W.J.: An expected gain-confidence limit criterion for portfolio selection. Manag. Sci. 10(1), 174–182 (1963)

    Article  Google Scholar 

  10. Czichowsky, C.: Time-consistent mean-variance portfolio selection in discrete and continuous time. Financ. Stochast. 17(2), 227–271 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  11. Chamberlain, G., Rothschild, M.: Arbitrage, factor structure, and mean-variance analysis on large asset markets NBER Working Paper, vol. 51, no. 5, pp. 1281–1304 (1984)

  12. Clarkson, G.P.: Portfolio Selection: A Simulation of Trust Investment. Prentice-Hall, Englewood Cliffs (1962)

    Google Scholar 

  13. Markowitz, H.: Portfolio selection*. J. Financ. 7(1), 77–91 (1952)

    Google Scholar 

  14. Merton, R.C.: Lifetime portfolio selection under uncertainty: the continuous-time case. Rev. Econ. Stat. 51(3), 247–257 (1969)

    Article  Google Scholar 

  15. Kroll, Y., Levy, H., Markowitz, H.M.: Mean-variance versus direct utility maximization. J. Financ. 39(1), 47–61 (1984)

    Article  Google Scholar 

  16. Maccheroni, F., Marinacci, M., Ruffino, D.: Alpha as ambiguity: robust mean-variance portfolio analysis. Econometrica 81(3), 1075–1113 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  17. Todd, G.P.: Mean-Variance Analysis in Portfolio Choice and Capital Markets, vol. 66. Wiley, New York (2000)

    Google Scholar 

  18. Tanaka, H., Guo, P., Türksen, I.B.: Portfolio selection based on fuzzy probabilities and possibility distributions. Fuzzy Sets Syst. 111(3), 387–397 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  19. Tse, S.T., Forsyth, P.A., Kennedy, J.S., Windcliff, H.: Comparison between the mean-variance optimal and the mean-quadratic-variation optimal trading strategies. Appl. Math. Financ. 20(5), 415–449 (2013)

    Article  MathSciNet  Google Scholar 

  20. Hao, F.F., Liu, Y.K., Wang, S.: “The variance formulas for triangular fuzzy random variables,” In: 2008 International Conference on Machine Learning and Cybernetics, (Vol. 1, pp. 612–617), IEEE, July 2008

  21. Zadeh, L.A.: Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1, 3–28 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  22. De Cooman, G., Kerre, E.E., Vanmassenhove, F.R.: Possibility theory: an integral theoretic approach. Fuzzy Sets Syst. 46(2), 287–299 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  23. Dubois, D., Prade, H.: Possibility Theory. Plenum, New York (1988)

    Book  MATH  Google Scholar 

  24. Klir, G.J., Yuan, B.: Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall International, Upper Saddle River, NJ (1995)

    MATH  Google Scholar 

  25. Klir, G.J.: On fuzzy-set interpretation of possibility theory. Fuzzy Sets Syst. 108(3), 263–273 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  26. Liu, B.D.: Toward fuzzy optimization without mathematical ambiguity. Fuzzy Optim. Decis. Mak. 1(1), 43–63 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  27. Liu, B.D.: Inequalities and convergence concepts of fuzzy and rough variables. Fuzzy Optim. Decis. Mak. 2(2), 87–100 (2003)

    Article  MathSciNet  Google Scholar 

  28. Liu, B.D.: Uncertainty Theory: An Introduction to its Axiomatic Foundations, vol. 154. Springer, Berlin (2004)

    MATH  Google Scholar 

  29. Liu, B.D.: Theory and Practice of Uncertain Programming. Physica-Verlag, Heidelberg (2002)

    Book  MATH  Google Scholar 

  30. Liu, B.D., Liu, Y.K.: Expected value of fuzzy variable and fuzzy expected value models. IEEE Trans. Fuzzy Syst. 10(4), 445–450 (2002)

    Article  Google Scholar 

  31. Liu, Y.K., Liu, B.D.: Fuzzy random variables: a scalar expected value operator. Fuzzy Optim. Decis. Mak 2(2), 143–160 (2003)

    Article  MathSciNet  Google Scholar 

  32. Liu, Y.K., Liu, B.D.: Expected value operator of random fuzzy variable and random fuzzy expected value models. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 11(2), 195–215 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  33. Liu, Y.K.: The approximation method for two-stage fuzzy random programming with recourse. IEEE Trans. Fuzzy Syst. 15(6), 1197–1208 (2007)

    Article  Google Scholar 

  34. Liu, Y.K., Gao, J.: The independence of fuzzy variables with applications to fuzzy random optimization. Int. J. Uncertain Fuzziness Knowl. Based Syst. 15(2), 1–20 (2007)

    Article  MathSciNet  Google Scholar 

  35. de Andrés-Sánchez, J., González-Vila Puchades, L.: Using fuzzy random variables in life annuities pricing. Fuzzy Sets Syst. 188(1), 27–44 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  36. Feng, X., Liu, Y.K.: Measurability criteria for fuzzy random vectors. Fuzzy Optim. Decis. Mak. 5(3), 245–253 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  37. Herrera, F., Herrera-Viedma, E.: Linguistic decision analysis: steps for solving decision problems under linguistic information. Fuzzy Sets Syst. 115(1), 67–82 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  38. Liu, H.W., Wang, G.J.: Multi-criteria decision-making methods based on intuitionistic fuzzy sets. Eur. J. Oper. Res. 179(1), 220–233 (2007)

    Article  MATH  Google Scholar 

  39. Li, X., Liu, B.D.: A sufficient and necessary condition for credibility measures. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 14(5), 527–535 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  40. Liu, X.: A review of the OWA determination methods: classification and some extensions. In: Yager, R.R., Kacprzyk, J., Beliakov, G. (eds.) Recent Developments in the Ordered Weighted Averaging Operators: Theory and Practice, pp. 49–90. Springer, Berlin (2011)

    Chapter  Google Scholar 

  41. Mao, S.S., Wang, J., Pu, X.: Advanced Mathematical Statistics. China Higher Education Press, Beijing and Springer, Berlin (1998)

    Google Scholar 

  42. Mao, S.S., Wang, J., Pu, X.: Advanced Mathematical Statistics, 2nd edn. Higher Education Press, Beijing (2006)

    Google Scholar 

  43. Nahmias, S.: Fuzzy variables. Fuzzy Sets Syst. 1(2), 97–110 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  44. Wang, P.Z.: Fuzzy contactibility and fuzzy variables. Fuzzy Sets Syst. 8(1), 81–92 (1982)

    Article  Google Scholar 

  45. Watada, J., Lin, L.C., Qiang, M., Lin, P.C.: A fuzzy random variable approach to restructuring of rough sets through statistical test. In: Kuznetsov, S.O., Ślęzak, D., Hepting, D.H., Mirkin, B.G. (eds.) Rough Sets, Fuzzy Sets, Data Mining and Granular Computing, pp. 269–277. Springer, Berlin (2009)

    Chapter  Google Scholar 

  46. Xu, Z.S.: An overview of methods for determining OWA weights. Int. J. Intell. Syst. 20(8), 843–865 (2005)

    Article  MATH  Google Scholar 

  47. Xu, Z.S.: Induced uncertain linguistic OWA operators applied to group decision making. Inf Fusion 7(2), 231–238 (2006)

    Article  Google Scholar 

  48. Xu, Z.S., Da, Q.-L.: An overview of operators for aggregating information. Int. J. Intell. Syst. 18(9), 953–969 (2003)

    Article  MATH  Google Scholar 

  49. Xu, Z.S.: Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 15(6), 1179–1187 (2007)

    Article  Google Scholar 

  50. Yager, R.R.: Determining equivalent values for possibilistic variables. IEEE Trans. Syst. Man Cybern. B Cybern. 31(1), 19–31 (2001)

    Article  Google Scholar 

  51. Yager, R.R.: On ordered weighted averaging aggregation operators in multi-criteria decision making. IEEE Trans. Syst. Man Cybern. B 18, 183–190 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  52. Yager, R.R., Kacprzyk, J., Beliakov, G.: Recent Developments on the Ordered Weighted Averaging Operators: Theory and Practice. Springer, Berlin (2011)

    Book  Google Scholar 

  53. Yager, R.R.: OWA aggregation of intuitionistic fuzzy sets. Int. J. Gen Syst 38(6), 617–641 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  54. Yager, R.R.: Applications and extensions of OWA aggregations. Int. J. Man Mach. Stud. 37(1), 103–122 (1992)

    Article  Google Scholar 

  55. Yeh, C.H., Chang, Y.H.: Modeling subjective evaluation for fuzzy group multicriteria decision making. Eur. J. Oper. Res. 194(2), 464–473 (2009)

    Article  MATH  Google Scholar 

  56. Ye, J.: Multicriteria fuzzy decision-making method based on a novel accuracy function under interval-valued intuitionistic fuzzy environment. Expert Syst. Appl. 36(3), 6899–6902 (2009)

    Article  Google Scholar 

  57. Ye, J.: Fuzzy decision-making method based on the weighted correlation coefficient under intuitionistic fuzzy environment. Eur. J. Oper. Res. 205(1), 202–204 (2010)

    Article  MATH  Google Scholar 

  58. Emrouznejad, A., Marra, M.: Ordered weighted averaging operators 1988–2014: a citation based literature survey. Int. J. Intell. Syst. 29(11), 994–1014 (2014)

    Article  Google Scholar 

  59. Chen, S.J., Chen, S.M.: A new method for handling multi-criteria fuzzy decision making problems using FN-IOWA operators. Cybern. Syst. 34(2), 109–137 (2003)

    Article  MATH  Google Scholar 

  60. Merigó, J.M.: Fuzzy multi-person decision making with fuzzy probabilistic aggregation operators. Int. J. Fuzzy Syst. 13(3), 163–174 (2011)

    MathSciNet  Google Scholar 

  61. Merigó, J.M., Casanovas, M.: The fuzzy generalized OWA operator and its application in strategic decision making. Cybern. Syst. 41(5), 359–370 (2010)

    Article  Google Scholar 

  62. Merigó, J.M., Casanovas, M., Liu, P.D.: Decision making with fuzzy induced heavy ordered weighted averaging operators. Int. J. Fuzzy Syst. 16(3), 277–289 (2014)

    Google Scholar 

  63. Merigó, J.M., Casanovas, M.: Fuzzy generalized hybrid aggregation operators and its application in decision making. Int. J. Fuzzy Syst. 12(1), 15–24 (2010)

    Google Scholar 

  64. Merigó, J.M., Casanovas, M.: Decision making with distance measures and linguistic aggregation operators. Int. J. Fuzzy Syst. 12(3), 190–198 (2010)

    Google Scholar 

  65. Merigó, J.M., Guillén, M., Sarabia, J.M.: The ordered weighted average in the variance and covariance. Int. J. Intell. Syst. 30(9), 985–1005 (2015)

    Article  Google Scholar 

  66. Zeng, S.Z., Wang, Q.F., Merigó, J.M., Pan, T.J.: Induced intuitionistic fuzzy ordered weighted averaging - weighted average operator and its application to business decision-making. Comput. Sci. Inf Syst 11(2), 839–857 (2014)

    Article  Google Scholar 

  67. Sadiq, R., Tesfamariam, S.: Probability density functions based weights for ordered weighted averaging (OWA) operators: an example of water quality indices. Eur. J. Oper. Res. 182(3), 1350–1368 (2007)

    Article  MATH  Google Scholar 

  68. Beliakov, G.: How to build aggregation operators from data. Int. J. Intell. Syst. 18(8), 903–923 (2003)

    Article  MATH  Google Scholar 

  69. Singh A., Kishor, A., Pal N.: Stancu OWA operator. IEEE Trans. Fuzzy Syst. 23(4), 1306–1313 (2015)

    Article  Google Scholar 

  70. Wang, Y.M., Parkan, C.: A minimax disparity approach for obtaining OWA operator weights. Inf. Sci. 175(1), 20–29 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  71. Ahn, B.S.: On the properties of OWA operator weights functions with constant level of orness. IEEE Trans. Fuzzy Syst. 14(4), 511–515 (2006)

    Article  Google Scholar 

  72. Deschrijver, G., Kerre, E.: Aggregation Operators in Interval-Valued Fuzzy and Atanassov’s Intuitionistic Fuzzy Set Theory[M]//Fuzzy Sets and Their Extensions: Representation, Aggregation and Models, pp. 183–203. Springer, Berlin (2008)

    Book  MATH  Google Scholar 

  73. Xia, M.M., Xu, Z.S.: Hesitant fuzzy information aggregation in decision making. Int. J. Approx. Reason. 52(3), 395–407 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  74. Rodríguez, R.M., Martínez, L., Herrera, F.: Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 20(1), 109–119 (2012)

    Article  Google Scholar 

Download references

Acknowledgments

This study was financially supported by the National Natural Science Foundation of China (Project Nos. NSFC71371156 and NSFC70971017) and partially by the Research Grants Council of the Hong Kong Special Administrative Region, China (Grant No. CityU-112111).

Author information

Authors and Affiliations

  1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu, 610031, Sichuan, People’s Republic of China

    Zhen-Song Chen & Yan-Lai Li

  2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Southwest Jiaotong University, Chengdu, 610031, Sichuan, People’s Republic of China

    Zhen-Song Chen & Yan-Lai Li

  3. Department of System Engineering and Engineering Management, City University of Hong Kong, 83 Tat Chee Avenue, Kowloon Tong, Hong Kong, People’s Republic of China

    Kwai-Sang Chin

Authors
  1. Zhen-Song Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Kwai-Sang Chin
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yan-Lai Li
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yan-Lai Li.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, ZS., Chin, KS. & Li, YL. A Framework for Triangular Fuzzy Random Multiple-Criteria Decision Making. Int. J. Fuzzy Syst. 18, 227–247 (2016). https://doi.org/10.1007/s40815-015-0109-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-015-0109-1

Keywords