Introduction

In decision-making problem, we face situations where some alternatives need to be evaluated with respect to some criteria in an uncertain environment. Multi-attribute decision-making (MADM) strategy helps us to evaluate and select the best alternative. For example, to choose a mobile phone, a customer would analyze whether the mobile phone model satisfies attributes such as good features, affordable price, hardware capacity and customer care.

Smarandache proposed neutrosophic set [1] based on neutrosophy in 1998. In 2010, Wang et al. [2] put forward single-valued neutrosophic set (SVNS) to handle uncertain, indeterminate and inconsistent data. SVNS, its extension and several hybrid neutrosophic sets have been studied in various fields such as MADM [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74], conflict resolution [75], image processing [76] and educational problem [77].

Ye [78] proposed trapezoidal neutrosophic number (TrNN) derived from SVNS and trapezoidal fuzzy number [79]. Deli and Subas [80] proposed a ranking strategy of TrNN and developed an MADM strategy. Liang et al. [81] defined score function, accuracy function and certainty function of single-valued trapezoidal neutrosophic number (SVTrNN) using center of gravity (COG). Biswas et al. [82] developed a value- and ambiguity-based ranking strategy for TrNNs and proposed an MADM strategy. Biswas et al. [83] established TOPSIS strategy for MADM in trapezoidal neutrosophic number (TrNN) environment. Pramanik and Mallick [84] developed a VIKOR strategy for a multi-attribute group decision making (MAGDM) in TrNN environment. Giri et al. [85] presented an MADM strategy in interval trapezoidal neutrosophic number environment.

TODIM [86] is one of the popular strategies to handle MAGDM in the neutrosophic environment. Qin et al. [87] developed the TODIM strategy for triangular intuitionistic fuzzy number. Wang and Li [88] developed a TODIM method for multi-valued neutrosophic number. In 2016, Zhang et al. [89] introduced a TODIM strategy with neutrosophic numbers. Pramanik et al. [90] established a TODIM strategy for neutrosophic cubic set environment. Pramanik et al. [91] grounded a TODIM strategy in bipolar neutrosophic set environment. To date, TODIM strategy in the TrNN environment has not been presented in the literature. To fill up this research gap, we develop a TODIM strategy to deal with MAGDM problems in TrNN environment. We also solve an MAGDM problem to explain the proposed TODIM strategy in the TrNN environment.

This paper is constructed as follows. In “Preliminaries”, we briefly describe a few definitions of trapezoidal fuzzy number, single-valued trapezoidal neutrosophic number, score function, accuracy function and Hamming distance between two trapezoidal neutrosophic fuzzy numbers. In “TODIM strategy for solving MAGDM problem under TrNN environment”, we briefly describe the extended TODIM strategy in the TrNN environment. In “Illustrative example”, we solve an illustrative numerical example using the proposed TODIM strategy. In “Conclusion”, we present the sensitivity analysis.

Preliminaries

In this section, we recall some basic definitions associated with neutrosophic set, trapezoidal neutrosophic set and TODIM strategy.

Definition 1

[2] Assume that H is a universal set. A single-valued neutrosophic set B in H is given by

$$ B = \{ h, < T_{B} (h),I_{B} (h),F_{B} (h) > \left| {h \in H} \right.\} , $$
(1)

where \( T_{B} (h):H \to [0,1],\,I_{B} (h):H \to [0,1] \) and \( F_{B} (h):H \to [0,1] \) with the condition \( 0 \le T_{B} (h) + I_{B} (h) + F_{B} (h) \le 3 \) for all \( h \in H \).The functions \( T_{B} (h),\,\,I_{B} (h) \) and \( F_{B} (h) \) are, respectively, the truth membership function, the indeterminacy membership function and the falsity membership function of the set B.

Definition 2

[79, 80] Let S be a trapezoidal neutrosophic number (TrNN). Then, its truth membership function is

$$ T_{S} (z) = \left\{ {\begin{array}{*{20}l} {\frac{{(z - k)t_{S} }}{(l - k)},} \hfill & {k \le z < l} \hfill \\ {t_{S} ,} \hfill & {l \le z \le m} \hfill \\ {\frac{{(n - z)t_{S} }}{(n - m)},} \hfill & {m < z \le n} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.. $$
(2)

Its indeterminacy membership function is

$$ I_{S} (z) = \left\{ {\begin{array}{*{20}l} {\frac{{(l - z) + (z - k^{\prime})i_{S} }}{{(l - k^{\prime})}},} \hfill & {k^{\prime} \le z < l} \hfill \\ {i_{S} ,} \hfill & {l \le z \le m} \hfill \\ {\frac{{z - m + (n^{\prime} - z)i_{S} }}{{n^{\prime} - m}},} \hfill & {m < z \le n^{\prime}} \hfill \\ {1,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.. $$
(3)

Its falsity membership function is

$$ F_{S} (z) = \left\{ {\begin{array}{*{20}l} {\frac{{l - z + (z - k^{\prime\prime})f_{S} }}{l - k},} \hfill & {k^{\prime\prime} \le z < l} \hfill \\ {f_{S} ,} \hfill & {l \le z \le m} \hfill \\ {\frac{{z - m + (n^{\prime\prime} - z)f_{S} }}{{n^{\prime\prime} - m}},} \hfill & {m < z \le n^{\prime\prime}} \hfill \\ {1,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right., $$
(4)

where \( 0 \le T_{S} (z) \le 1,\,0 \le I_{S} (z) \le 1 \), \( 0 \le F_{S} (z) \le 1 \) and \( 0 \le T_{S} (z) + I_{S} (z) + F_{S} (z) \le 3; \, k,l,m,n \in R. \) Then \( S = ([k,l,m,n];\,t_{S} ,i_{S} ,f_{S} ) \) is called a TrNN.

If \( 0 \le k \le l \le m \le n \), then m is called a positive TrNN. If \( k \le l \le m \le n \le 0 \), then S is called a negative TrNN. If \( 0 \le k \le l \le m \le n \le 1 \) and \( T_{S} ,I_{S} ,F_{S} \in [0,1] \), then X is called a normalized TrNN, which is used in this paper. The membership functions are presented in Fig. 1.

Fig. 1
figure 1

Truth membership, indeterminacy membership and falsity membership functions of TrNN

Full size image

Definition 3

[81] Let \( H = [k,l,m,n] \) be a trapezoidal fuzzy number on R, and \( k \le l \le m \le n; \) then, the center of gravity (COG) of H is defined by:

$$ {\text{COG}}(H) = \left\{ {\begin{array}{*{20}l} H \hfill & {{\text{if }}k = l = m = n = H} \hfill \\ {\frac{1}{3}\left[ {k + l + m + n - \frac{mn - kl}{m + n - l - k}} \right]} \hfill & {{\text{otherwise}} .} \hfill \\ \end{array} } \right. $$
(5)

Definition 4

[81] Let \( g = \langle (k,l,m,n);\,T_{g} ,I_{g} ,F_{g} \rangle \) be a TrNN. Then the score function \( S(g) \), accuracy function \( {\text{Ac}}(g) \) and certainty function \( E(g) \) of TrNN are defined by

$$ S(g) = {\text{COG}}(H) \times \frac{{(2 + T_{g} - I_{g} - F_{g} )}}{3}, $$
(6)
$$ {\text{Ac}}(g) = {\text{COG}}(H) \times (T_{g} - F_{g} ), $$
(7)
$$ E(g) = {\text{COG}}(H) \times T_{g} . $$
(8)

Here, COG(H) is defined in (5).

Definition 5

[81] Comparison of two TrNNs:

Let \( g_{1} = \langle (k_{1} ,l_{1} ,m_{1} ,n_{1} );\,T_{{g_{1} }} ,I_{{g_{1} }} ,F_{{g_{1} }} \rangle \) and \( g_{2} = \langle (k_{2} ,l_{2} ,m_{2} ,n_{2} );\,T_{{g_{2} }} ,I_{{g_{2} }} ,F_{{g_{2} }} \rangle \) be any two TrNNs in S. The comparison between g1 and g2 is stated as follows:

  1. 1.

    If Sc(\( g_{1} \)) > Sc(\( g_{2} \)), then \( g_{1} \) > \( g_{2} . \)

  2. 2.

    If Sc(\( g_{1} \)) = Sc(\( g_{2} \)) and Ac(\( g_{1} \)) > Ac(\( g_{2} \)), then \( g_{1} \) > \( g_{2} . \)

  3. 3.

    If Sc(\( g_{1} \)) = Sc(\( g_{2} \)) and Ac(\( g_{1} \)) < Ac(\( g_{2} \)), then \( g_{1} \) < \( g_{2} . \)

  4. 4.

    If Sc(\( g_{1} \)) = Sc(\( g_{2} \)) and Ac(\( g_{1} \)) = Ac(\( g_{2} \)), and E(\( g_{1} \)) > E(\( g_{2} \)), \( g_{1} \) > \( g_{2} \) and when E(\( g_{1} \)) < E(\( g_{2} \)), then \( g_{1} \) < \( g_{2} \) and \( g_{1} \) > \( g_{2} \) when E(\( g_{1} \)) = E(\( g_{2} \)).

Definition 6

[83] Let \( g_{1} = ([k_{1} ,l_{1} ,m_{1} ,n_{1} ];\,t_{{g_{1} }} ,i_{{g_{1} }} ,f_{{g_{1} }} ) \) and \( g_{2} = ([k_{2} ,l_{2} ,m_{2} ,n_{2} ];\,t_{{g_{2} }} ,i_{{g_{2} }} f_{{g_{2} }} ) \) be any two TrNNs, then the normalized Hamming distance between \( g_{1} \) and \( g_{2} \) is defined as follows:

$$ d(g_{1} ,g_{2} ) = \frac{1}{12}\left( \begin{aligned} \left| {k_{1} (2 + t_{{g_{1} }} - i_{{g_{1} }} - f_{{g_{1} }} ) - k_{2} (2 + t_{{g_{2} }} - i_{{g_{2} }} - f_{{g_{2} }} )} \right| + \left| {l_{1} (2 + t_{{g_{1} }} - i_{{g_{1} }} - f_{{g_{1} }} ) - l_{2} (2 + t_{{g_{2} }} - i_{{g_{2} }} - f_{{g_{2} }} )} \right| \hfill \\ + \left| {m_{1} (2 + t_{{g_{1} }} - i_{{g_{1} }} - f_{{g_{1} }} ) - m_{2} (2 + t_{{g_{2} }} - i_{{g_{2} }} - f_{{g_{2} }} )} \right| + \left| {n_{1} (2 + t_{{g_{1} }} - i_{{g_{1} }} - f_{{g_{1} }} ) - n_{2} (2 + t_{{g_{2} }} - i_{{g_{2} }} - f_{{g_{2} }} )} \right| \hfill \\ \end{aligned} \right). $$
(9)

Standardize the decision matrix

Assume that \( D = (c_{lm} )_{p \times q} \) is a neutrosophic decision matrix, where \( \tilde{c}_{l\,m} = ([c_{l\,m}^{1} ,c_{l\,m}^{2} ,c_{l\,m}^{3} ,c_{l\,m}^{4} ];\,t_{{\tilde{c}_{l\,m} }} ,i_{{\tilde{c}_{l\,m} }} ,f_{{\tilde{c}_{l\,m} }} ) \) is the rating value of alternative \( Y_{l} \) with respect to attribute \( Z_{m} \). To remove the effects derived from different physical dimensions, the decision matrix \( (c_{l\,m} )_{p \times q} \) is standardized. We employ the technique [83] to obtain the standardized decision matrix \( Z^{*} = (\tilde{z}_{l\,m} )_{p \times q} \), in which the component \( z_{lm}^{k} \) of the entry \( \tilde{z}_{ij} = ([z_{l\,m}^{1} ,\,z_{l\,m}^{2} ,z_{l\,m}^{3} ,z_{l\,m}^{4} ];\,t_{{\tilde{z}_{l\,m} }} ,i_{{\tilde{z}_{l\,m} }} ,f_{{\tilde{z}_{l\,m} }} ) \) in the matrix S is considered as:

  1. 1.

    For benefit type attributes:

    $$ \tilde{z}_{lm} = \left. {\left( {\left[ {\frac{{c_{lm}^{1} }}{{h_{m}^{ + } }},\frac{{c_{lm}^{2} }}{{h_{m}^{ + } }},\frac{{c_{lm}^{3} }}{{h_{m}^{ + } }},\frac{{c_{lm}^{4} }}{{h_{m}^{ + } }}} \right];\,t_{{\tilde{z}_{lm} }} ,i_{{\tilde{z}_{lm} }} ,f_{{\tilde{z}_{lm} }} } \right)} \right\}. $$
    (10)
  2. 2.

    For cost type attributes:

    $$ \tilde{z}_{lm} = \left( {\left[ {\frac{{h_{m}^{ - } }}{{c_{lm}^{4} }},\frac{{h_{m}^{ - } }}{{c_{lm}^{3} }},\frac{{h_{m}^{ - } }}{{c_{lm}^{2} }},\frac{{h_{m}^{ - } }}{{c_{lm}^{1} }}} \right];\,t_{{\tilde{z}_{lm} }} ,i_{{\tilde{z}_{lm} }} ,f_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z}_{lm} }} } \right). $$
    (11)

Here, \( h_{m}^{ + } = \hbox{max} \{ c_{lm}^{4} \left| {l = 1,2, \ldots ,p\} } \right. \) and \( h_{m}^{ - } = \hbox{min} \{ b_{lm}^{1} \left| {l = 1,2, \ldots ,p} \right.\} \) for m = 1, 2,…, q.

Then we obtain the following standardized decision matrix:

$$ Z^{*} = (\tilde{z}_{lm} )_{p \times q} = \left( {\begin{array}{*{20}c} {z_{11} } & {z_{12} } & \ldots & {z_{1q} } \\ {z_{21} } & {z_{22} } & \ldots & {z_{2q} } \\ \ldots & \ldots & \ldots & \ldots \\ {z_{p1} } & {z_{p2} } & \ldots & {z_{pq} } \\ \end{array} } \right). $$
(12)

TODIM strategy for solving MAGDM problem under TrNN environment

In this section, we describe the proposed TODIM strategy to solve the MAGDM problem in TrNN environment. In the section process, we propose an MAGDM strategy in TrNN environment. Assume that \( u^{\prime} = \{ u^{\prime}_{1} ,u^{\prime}_{2} , \ldots ,u^{\prime}_{r} \} \) and \( v^{\prime} = \{ v^{\prime}_{1} ,v^{\prime}_{2} , \ldots ,v^{\prime}_{s} \} \) are the alternatives and criteria. Assume that \( w^{\prime} = \{ w^{\prime}_{1} ,w^{\prime}_{2} , \ldots ,w^{\prime}_{s} \} \) is the weight vector of the criteria satisfying \( w^{\prime}_{k} > 0 \) and \( \sum\nolimits_{k = 1}^{s} {w^{\prime}_{k} = 1} \). Also assume that \( D^{\prime} = \{ D^{\prime}_{1} ,D^{\prime}_{2} , \ldots ,D^{\prime}_{h} \} \) is the set of t decision makers and \( \lambda^{\prime} = \{ \lambda^{\prime}_{1} ,\lambda^{\prime}_{2} , \ldots ,\lambda^{\prime}_{h} \} \) is the set of weight vectors of decision makers where \( \lambda^{\prime}_{l} > 0 \) and \( \sum\nolimits_{l = 1}^{h} {\lambda^{\prime}_{l} = 1} . \)

The proposed TODIM strategy is developed using the following steps (see Fig. 2).

Fig. 2
figure 2

TODIM strategy in TrNN environment

Full size image

Step 1: Let \( D^{M} = (p_{cd}^{M} )_{m \times n} \) be the Mth decision matrix, where information about the alternative \( u^{\prime}_{i} \) is provided by the decision maker \( D_{M} \) with respect to attribute \( v^{\prime}_{j} (j = 1,2, \ldots ,s) \). The Mth decision matrix denoted by \( D^{M} \) is defined as follows:

$$ D^{M} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ \ldots \\ {u^{\prime}_{r} } \\ \end{array} \begin{array}{*{20}c} {v^{\prime}_{1} } \\ {p_{11}^{M} } \\ {p_{12}^{M} } \\ \ldots \\ {p_{r1}^{M} } \\ \end{array} \begin{array}{*{20}c} {v^{\prime}_{2} } \\ {p_{12}^{M} } \\ {p_{22}^{M} } \\ \ldots \\ {p_{r2}^{M} } \\ \end{array} \begin{array}{*{20}c} \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ \end{array} \begin{array}{*{20}c} {v^{\prime}_{s} } \\ {p_{1s}^{M} } \\ {p_{2s}^{M} } \\ \ldots \\ {p_{rs}^{M} } \\ \end{array} } \right). $$
(13)

Here, M = 1, 2,…, h; c = 1,2,…, r; d = 1,2,…, s.

Step 2: To standardize the benefit criteria, we use Eq. (11) and for cost criteria we use (12).

After standardizing, the decision matrix reduces to

$$ D^{M} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ \ldots \\ {u^{\prime}_{r} } \\ \end{array} \begin{array}{*{20}c} {v^{\prime}_{1} } \\ {\tilde{p}_{11}^{M} } \\ {\tilde{p}_{12}^{M} } \\ \ldots \\ {\tilde{p}_{r1}^{M} } \\ \end{array} \begin{array}{*{20}c} {v^{\prime}_{2} } \\ {\tilde{p}_{12}^{M} } \\ {\tilde{p}_{22}^{M} } \\ \ldots \\ {\tilde{p}_{r2}^{M} } \\ \end{array} \begin{array}{*{20}c} \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ \end{array} \begin{array}{*{20}c} {v^{\prime}_{s} } \\ {\tilde{p}_{1s}^{M} } \\ {\tilde{p}_{2s}^{M} } \\ \ldots \\ {\tilde{p}_{rs}^{M} } \\ \end{array} } \right). $$
(14)

Step 3: We calculate relative weight \( w^{\prime}_{EC} \) of each criterion by the following equation:

$$ w^{\prime}_{EC} = \frac{{w^{\prime}_{E} }}{{w^{\prime}_{C} }}. $$
(15)

Here, \( w^{\prime}_{C} = \hbox{max} \{ w^{\prime}_{1} ,w^{\prime}_{2} , \ldots ,w^{\prime}_{s} \} . \)

Step 4: Using Eq. (6), we calculate the score value of each alternative w.r.t. each criterion of the decision matrix (14).

Step 5: To calculate the accuracy value of each alternative w.r.t each criterion, we use Eq. (7).

Step 6: We construct the dominance matrix of each alternative \( u^{\prime}_{i} \) with respect to the criteria of the Mth decision maker \( D_{M} \) by the following equation:

$$ \left. \begin{aligned} \sigma_{c}^{M} (p_{i} ,p_{j} ) = \sqrt {\frac{{w^{\prime}_{EC} }}{{\sum\limits_{C = 1}^{s} {w^{\prime}_{EC} } }}d(\tilde{p}_{ic}^{M} ,\tilde{p}_{jc}^{M} )} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\tilde{p}_{ic}^{M} > \tilde{p}_{jc}^{M} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\,\tilde{p}_{ic}^{M} = \tilde{p}_{jc}^{M} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - \frac{1}{\gamma }\sqrt {\frac{{\sum\limits_{C = 1}^{s} {w^{\prime}_{EC} } }}{{w^{\prime}_{EC} }}d(\tilde{p}_{ic}^{M} ,\tilde{p}_{jc}^{M} )} ,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,\tilde{p}_{ic}^{M} < \tilde{p}_{jc}^{M} \hfill \\ \end{aligned} \right\}, $$
(16)

where \( \gamma \) denotes the decay factor of loss and \( \gamma > 0 \).

Step 7: To obtain the individual final dominance matrix, we use Eq. (17) which is described as:

$$ \psi_{M} = \sum\limits_{c = 1}^{s} {\sigma_{c}^{M} (p_{i} ,p_{j} )} . $$
(17)

Step 8: We calculate the aggregated dominance matrix by Eq. (18):

$$ \psi (p_{i} ,p_{j} ) = \sum\limits_{M = 1}^{t} {\lambda_{M} \psi_{M} (p_{i} ,p_{j} )} . $$
(18)

Step 9: To calculate the global value of each alternative, we use Eq. (19):

$$ \tau_{i} = \frac{{\sum\nolimits_{j = 1}^{s} {\psi (p_{i} ,p_{j} ) - \mathop {\hbox{min} }\nolimits_{1 \le i \le r} \left( {\sum\nolimits_{j = 1}^{s} {\psi (p_{i} ,p_{j} )} } \right)} }}{{\mathop {\hbox{max} }\limits_{1 \le i \le r} \left( {\sum\nolimits_{j = 1}^{s} {\psi (p_{i} ,p_{j} )} } \right) - \mathop {\hbox{min} }\nolimits_{1 \le i \le r} \left( {\sum\nolimits_{j = 1}^{s} {\psi (p_{i} ,p_{j} )} } \right)}}. $$
(19)

Step 10: We rank the global values of the alternatives in descending order. The highest global value is the best alternative.

Illustrative example

In this section, we demonstrate an example to show the applicability and effectiveness of the proposed strategy. To illustrate the proposed TODIM strategy, we solve an MAGDM problem adapted from [84]. Suppose that an investment company intends to invest a sum of money in the best option. The company constitutes a board of decision makers with three decision makers. The decision makers determine the alternatives to investing money.

The alternatives are:

  1. 1.

    Computer company \( (u^{\prime}_{1} ). \)

  2. 2.

    Arms company \( (u^{\prime}_{2} ). \)

  3. 3.

    Car company \( (u^{\prime}_{3} ). \)

  4. 4.

    Food company \( (u^{\prime}_{4} ). \).

The decision makers take the decision based on the following three attributes:

  1. 1.

    Risk factor \( (v^{\prime}_{1} ). \)

  2. 2.

    Growth factor \( (v^{\prime}_{2} ). \)

  3. 3.

    Environment impact \( (v^{\prime}_{3} ). \).

Assume that the weight of attributes and decision makers are \( w^{\prime} \) = (0.3, 0.5, 0.2)T and \( \lambda \) = (0.36, 0.30, 0.34)T. Now we apply the proposed strategy to solve the problem.

Step 1: Consider the decision matrix in which \( u^{\prime}_{1} ,u^{\prime}_{2} ,u^{\prime}_{3} \) and \( u^{\prime}_{4} \) represent the alternatives, and \( v^{\prime}_{1} ,\,v^{\prime}_{2} \) and \( v^{\prime}_{3} \) represent the criteria.

Decision matrix for X1:

$$ M^{1} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \begin{array}{*{20}c} {v^{\prime}_{1} } \\ {([0.4,0.5,0.5,0.6];\;0.3,0.1,0.2)} \\ {([0.3,0.3,0.4,0.4];\;0.5,0.3,0.4)} \\ {([0.4,0.4,0.5,0.6];\;0.4,0.3,0.3)} \\ {([0.3,0.4,0.5,0.5];\;0.2,0.3,0.1)} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{2} } \\ {([0.3,0.4,0.5,0.5];\;0.4,0.2,0.3)} \\ {([0.2,0.3,0.3,0.3];\;0.5,0.2,0.5)} \\ {([0.3,0.4,0.5,0.6];\;0.3,0.4,0.2)} \\ {([0.2,0.3,0.3,0.6];\;0.5,0.2,0.2)} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{3} } \\ {([0.2,0.3,0.4,0.5];\;0.3,0.3,0.2)} \\ {([0.4,0.5,0.6,0.6];\;0.4,0.2,0.3)} \\ {([0.1,0.2,0.2,0.3];\;0.3,0.2,0.1)} \\ {([0.3,0.4,0.7,0.7];\;0.5,0.4,0.3)} \\ \end{array} } \right). $$

Decision matrix for X2:

$$ M^{2} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \begin{array}{*{20}c} {v^{\prime}_{1} } \\ {([0.6,0.7,0.7,0.8];\;0.3,0.4,0.1)} \\ {([0.5,0.6,0.7,0.7];\;0.5,0.3,0.4)} \\ {([0.4,0.5,0.6,0.6];\;0.8,0.3,0.4)} \\ {([0.3,0.5,0.6,0.7];\;0.7,0.4,0.5)} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{2} } \\ {([0.5,0.6,0.6,0.7];\;0.5,0.4,0.3)} \\ {([0.2,0.3,0.5,0.5];\;0.4,0.5,0.3)} \\ {([0.3,0.4,0.5,0.5];\;0.3,0.4,0.5)} \\ {([0.4,0.5,0.6,0.6];\;0.4,0.4,0.3)} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{3} } \\ {([0.3,0.5,0.6,0.7];\;0.5,0.4,0.2)} \\ {([0.4,0.5,0.6,0.7];\;0.4,0.2,0.3)} \\ {([0.6,0.6,0.7,0.7];\;0.2,0.3,0.1)} \\ {([0.5,0.6,0.7,0.8];\;0.5,0.1,0.2)} \\ \end{array} } \right). $$

Decision matrix for X3:

$$ M^{3} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \begin{array}{*{20}c} {v^{\prime}_{1} } \\ {([0.4,0.5,0.6,0.6];\;0.3,0.2,0.2)} \\ {([0.5,0.6,0.6,0.7];\;0.4,0.5,0.6)} \\ {([0.6,0.7,0.7,0.8];\;0.4,0.3,0.3)} \\ {([0.5,0.5,0.7,0.7];\;0.2,0.1,0.1)} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{2} } \\ {([0.4,0.5,0.5,0.5];\;0.3,0.5,0.2)} \\ {([0.3,0.5,0.5,0.6];\;0.8,0.2,0.3)} \\ {([0.6,0.6,0.6,0.7];\;0.6,0.5,0.4)} \\ {([0.5,0.5,0.6,0.8];\;0.3,0.2,0.2)} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{3} } \\ {([0.2,0.3,0.4,0.4];\;0.4,0.3,0.3)} \\ {([0.3,0.4,0.4,0.5];\;0.5,0.3,0.2)} \\ {([0.4,0.5,0.6,0.6];\;0.4,0.2,0.2)} \\ {([0.3,0.5,0.5,0.7];\;0.5,0.2,0.3)} \\ \end{array} } \right). $$

Step 2: Since all the criteria are of the benefit type, we do not need to standardize the decision matrix.

Step 3: In this step, we obtain the relative weight for each criteria using Eq. (15) as

$$ w^{\prime}_{{EC_{1} }} = 0.6,\quad w^{\prime}_{{EC_{2} }} = 1,\quad w^{\prime}_{{EC_{3} }} = 0.4. $$

Step 4: Using Eq. (6), we obtain the score value of each alternative with respect to each criterion. The score values are presented in matrix form as shown (see matrix 1, matrix 2 and matrix 3).

Matrix 1: Score value for M1

$$ \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{1} } \\ {0.33} \\ {0.21} \\ {0.28} \\ {0.25} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{2} } \\ {0.27} \\ {0.16} \\ {0.25} \\ {0.26} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{3} } \\ {0.21} \\ {0.33} \\ {0.13} \\ {0.31} \\ \end{array} } \right). $$

Matrix 2: Score value for M2

$$ \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{1} } \\ {0.42} \\ {0.37} \\ {0.36} \\ {0.31} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{2} } \\ {0.36} \\ {0.2} \\ {0.2} \\ {0.3} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{3} } \\ {0.33} \\ {0.35} \\ {0.39} \\ {0.48} \\ \end{array} } \right). $$

Matrix 3: Score value for M3

$$ \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{1} } \\ {0.33} \\ {0.26} \\ {0.42} \\ {0.4} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{2} } \\ {0.25} \\ {0.36} \\ {0.35} \\ {0.38} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{3} } \\ {0.19} \\ {0.27} \\ {0.35} \\ {0.33} \\ \end{array} } \right). $$

Step 5: In this step, we calculate the accuracy function using Eq. (7).

Matrix 4: Accuracy value for M1

$$ \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{1} } \\ {0.05} \\ {0.03} \\ {0.05} \\ {0.04} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{2} } \\ {0.04} \\ 0 \\ {0.04} \\ {0.11} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{3} } \\ {0.04} \\ {0.05} \\ {0.04} \\ {0.10} \\ \end{array} } \right). $$

Matrix 5: Accuracy value for M2

$$ \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{1} } \\ {0.14} \\ {0.06} \\ {0.21} \\ {0.12} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{2} } \\ {0.12} \\ {0.03} \\ {0.08} \\ {0.05} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{3} } \\ {0.19} \\ {0.06} \\ {0.06} \\ {0.20} \\ \end{array} } \right). $$

Matrix 6: Accuracy value for M3

$$ \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{1} } \\ {0.05} \\ {0.12} \\ {0.07} \\ {0.06} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{2} } \\ {0.05} \\ {0.23} \\ {0.13} \\ {0.06} \\ \end{array} \quad \begin{array}{*{20}c} {v^{\prime}_{3} } \\ {0.03} \\ {0.12} \\ {0.10} \\ {0.10} \\ \end{array} } \right). $$

Step 6: Using Eq. (16), we calculate the dominance matrix (taking \( \gamma \) = 1) (matrices 7–15).

Matrix 7: Dominance matrix \( \sigma_{1}^{1} \)

$$ \sigma_{1}^{1} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{1} } \\ 0 \\ { - 0.6411} \\ { - 0.4012} \\ { - 0.5056} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{2} } \\ {0.1923} \\ 0 \\ {0.1517} \\ {0.1162} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{3} } \\ {0.1204} \\ { - 0.5109} \\ 0 \\ { - 0.3162} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{4} } \\ {0.1533} \\ { - 0.3873} \\ {0.0949} \\ 0 \\ \end{array} } \right). $$

Matrix 8: Dominance matrix \( \sigma_{2}^{1} \)

$$ \sigma_{2}^{1} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{1} } \\ 0 \\ { - 0.4565} \\ { - 0.1959} \\ { - 0.3896} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{2} } \\ {0.2282} \\ 0 \\ {0.1384} \\ {0.2} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{3} } \\ {0.2135} \\ { - 0.2768} \\ 0 \\ {0.1549} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{4} } \\ {0.1947} \\ { - 0.4} \\ { - 0.4082} \\ 0 \\ \end{array} } \right). $$

Matrix 9: Dominance matrix \( \sigma_{3}^{1} \)

$$ \sigma_{3}^{1} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{1} } \\ 0 \\ {0.1565} \\ { - 0.6192} \\ {0.1449} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{2} } \\ { - 0.7826} \\ 0 \\ { - 0.9980} \\ { - 0.5362} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{3} } \\ {0.1238} \\ {0.1996} \\ 0 \\ {0.1906} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{4} } \\ { - 0.7246} \\ {0.1072} \\ { - 0.9531} \\ 0 \\ \end{array} } \right). $$

Matrix 10: Dominance matrix \( \sigma_{1}^{2} \)

$$ \sigma_{1}^{2} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{1} } \\ 0 \\ { - 0.3873} \\ { - 0.4183} \\ { - 0.6279} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{2} } \\ {0.1162} \\ 0 \\ { - 0.1581} \\ { - 0.4535} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{3} } \\ {0.1255} \\ {0.0474} \\ 0 \\ { - 0.4183} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{4} } \\ {0.1884} \\ {0.1360} \\ {0.1254} \\ 0 \\ \end{array} } \right). $$

Matrix 11: Dominance matrix \( \sigma_{2}^{2} \)

$$ \sigma_{2}^{2} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{1} } \\ 0 \\ { - 0.5657} \\ { - 0.5687} \\ { - 0.3535} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{2} } \\ {0.2828} \\ 0 \\ {0.1258} \\ {0.2208} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{3} } \\ {0.2843} \\ { - 0.2517} \\ 0 \\ {0.2227} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{4} } \\ {0.1768} \\ { - 0.4416} \\ { - 0.4454} \\ 0 \\ \end{array} } \right). $$

Matrix 12: Dominance matrix \( \sigma_{3}^{2} \)

$$ \sigma_{3}^{2} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{1} } \\ 0 \\ {0.0562} \\ {0.1176} \\ {0.1698} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{2} } \\ { - 0.2811} \\ 0 \\ {0.1032} \\ {0.1602} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{3} } \\ { - 0.5882} \\ { - 0.5162} \\ 0 \\ {0.1317} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{4} } \\ { - 0.8491} \\ { - 0.8009} \\ { - 0.6584} \\ 0 \\ \end{array} } \right). $$

Matrix 13: Dominance matrix \( \sigma_{1}^{3} \)

$$ \sigma_{1}^{3} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{1} } \\ 0 \\ { - 0.4915} \\ {0.1620} \\ {0.1423} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{2} } \\ {0.1475} \\ 0 \\ {0.2191} \\ {0.2049} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{3} } \\ { - 0.5401} \\ { - 0.7303} \\ 0 \\ { - 0.5868} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{4} } \\ { - 0.4564} \\ { - 0.6831} \\ {0.1760} \\ 0 \\ \end{array} } \right). $$

Matrix 14: Dominance matrix \( \sigma_{2}^{3} \)

$$ \sigma_{2}^{3} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{1} } \\ 0 \\ {0.2354} \\ {0.2245} \\ {0.2517} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{2} } \\ { - 0.4707} \\ 0 \\ { - 0.3605} \\ {0.1594} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{3} } \\ { - 0.4490} \\ {0.1809} \\ 0 \\ {0.1568} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{4} } \\ { - 0.5034} \\ { - 0.3187} \\ { - 0.3137} \\ 0 \\ \end{array} } \right). $$

Matrix 15: Dominance matrix \( \sigma_{3}^{3} \)

$$ \sigma_{3}^{3} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{1} } \\ 0 \\ {0.1197} \\ {0.1761} \\ {0.1663} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{2} } \\ { - 0.5987} \\ 0 \\ {0.1291} \\ {0.1155} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{3} } \\ { - 0.8803} \\ { - 0.6454} \\ 0 \\ { - 0.5} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{4} } \\ { - 0.8316} \\ { - 0.5775} \\ {0.1} \\ 0 \\ \end{array} } \right). $$

Step 7: Using Eq. (17), we constructed the final dominance matrix (matrices 16–18).

Matrix 16: Final dominance matrix \( \psi_{1} \)

$$ \varPsi_{1} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{1} } \\ 0 \\ { - 0.9411} \\ { - 1.2163} \\ { - 0.7503} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{2} } \\ { - 0.3621} \\ 0 \\ { - 0.7079} \\ { - 0.22} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{3} } \\ {0.4577} \\ { - 0.6681} \\ 0 \\ {0.0293} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{4} } \\ { - 0.3766} \\ { - 0.6801} \\ { - 1.2664} \\ 0 \\ \end{array} } \right). $$

Matrix 17: Final dominance matrix \( \psi_{2} \)

$$ \psi_{2} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{1} } \\ 0 \\ { - 0.8968} \\ { - 0.8694} \\ { - 0.8116} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{2} } \\ {0.1179} \\ 0 \\ {0.0709} \\ { - 0.0725} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{3} } \\ { - 0.1784} \\ { - 0.7205} \\ 0 \\ { - 0.0639} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{4} } \\ { - 0.4839} \\ { - 1.1065} \\ { - 0.9784} \\ 0 \\ \end{array} } \right). $$

Matrix 18: Final dominance matrix \( \psi_{3} \)

$$ \psi_{3} = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{1} } \\ 0 \\ { - .1364} \\ {0.5626} \\ {0.5603} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{2} } \\ { - 0.9219} \\ 0 \\ { - 0.0123} \\ {0.4798} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{3} } \\ { - 1.8694} \\ { - 1.1948} \\ 0 \\ { - 0.93} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{4} } \\ { - 1.7914} \\ { - 1.5793} \\ {0.0377} \\ 0 \\ \end{array} } \right). $$

Step 8: Using Eq. (18), we construct the aggregated dominance matrix.

Matrix 19: Aggregated dominance matrix

$$ \psi = \left( {\begin{array}{*{20}c} {} \\ {u^{\prime}_{1} } \\ {u^{\prime}_{2} } \\ {u^{\prime}_{3} } \\ {u^{\prime}_{4} } \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{1} } \\ 0 \\ { - 0.6542} \\ { - 0.5074} \\ { - 0.3231} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{2} } \\ { - 0.4084} \\ 0 \\ { - 0.2378} \\ {0.0622} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{3} } \\ { - 0.5243} \\ { - 0.8629} \\ 0 \\ { - 0.3248} \\ \end{array} \quad \begin{array}{*{20}c} {u^{\prime}_{4} } \\ { - 0.8898} \\ { - 1.1137} \\ { - 0.5327} \\ 0 \\ \end{array} } \right). $$

Step 9: Using Eq. (19), we calculate the global value \( \tau_{i} \)

$$ \tau_{1} = 0.3952,\quad \tau_{2} = 0,\quad \tau_{3} = 0.6611,\quad \tau_{4} = 1. $$

Step 10: Since

$$ \tau_{4} > \tau_{3} > \tau_{1} > \tau_{2} , $$

the ranking order of the alternatives is

$$ u^{\prime}_{4} > u^{\prime}_{3} > u^{\prime}_{1} > u^{\prime}_{2} . $$

Thus, we see that the food company is the best option to invest in.

Sensitive analysis on influence of the parameter γ to ranking order

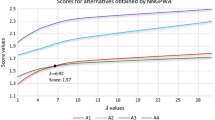
We see that for different values of γ, we obtain different global values that affect the ranking order of the alternatives. When γ = 1, 2, 3, 4, 5, the ranking order of the alternatives are presented in Table 1. When γ = 1, 2, 3, 4, and 5, \( u^{\prime}_{4} \) is the best alternative and \( u^{\prime}_{2} \) is the worst alternative. Also we see that for γ = 2, γ = 3, and γ = 4, the ranking order of the alternatives remains the same as \( u^{\prime}_{4} > u^{\prime}_{1} > u^{\prime}_{3} > u^{\prime}_{2} \). For γ = 1, and γ = 5, we obtain the ranking order as \( u^{\prime}_{4} > u^{\prime}_{3} > u^{\prime}_{1} > u^{\prime}_{2} \). So we obtain two different ranking orders, but the best alternative remains the same as the food company \( (u^{\prime}_{4} ) \) and the worst alternative is the arms company \( (u^{\prime}_{2} ) \). Therefore, we can say that the ranking order of the alternatives depends on the decay factor of loss γ.

Table 1 Ranking order of alternatives for different values of parameter γ
Full size table

Conclusion

We have developed a trapezoidal neutrosophic multiple attribute group decision-making strategy, namely TODIM strategy, in which the evaluation values of alternatives over the attributes assume the form of trapezoidal neutrosophic numbers.

The advantage of the proposed strategy is that it is more suitable for solving multiple attribute group decision-making problems with trapezoidal neutrosophic information because trapezoidal neutrosophic numbers can handle indeterminate and inconsistent information and are the extension of trapezoidal intuitionistic fuzzy numbers.

We also illustrate the developed TODIM strategy by solving a numerical example of the investment problem. We hope that the proposed TODIM strategy can be applied to solve real-world decision-making problems such as brick selection [92, 93], teacher selection [94] and weaver selection [95].