3D hydroelastic analysis of very large floating bodies over variable bathymetry regions

Abstract

The coupled-mode model developed by Belibassakis and Athanassoulis (J Fluid Mech 531:221–249, 2005) is extended and applied to the hydroelastic analysis of three-dimensional large floating bodies of shallow draft lying over variable bathymetry regions. The method is also applicable to the problem of wave interaction with ice sheets of small thickness. A general bathymetry is assumed, characterized by a continuous depth function, joining two regions of constant, but possibly different, depth. We consider the scattering problem of harmonic incident surface waves, under the combined effects of variable bathymetry and a floating elastic plate of orthogonal planform shape. Under the assumption of small-amplitude waves and plate deflections, the hydroelastic problem is formulated within the context of linearized water-wave and thin elastic-plate theory. To consistently treat the wave field beneath the elastic floating plate, down to the sloping bottom boundary, a complete, local, hydroelastic-mode series expansion of the wave field is used, enhanced by an appropriate sloping-bottom mode. The latter enables the consistent satisfaction of the Neumann bottom-boundary condition on a general topography. Numerical results concerning floating structures over flat and inhomogeneous seabed are presented, and the effects of wave direction, bottom slope and bottom corrugations on the hydroelastic responses are discussed.

1 Introduction

Floating deformable bodies of large horizontal dimensions are subjected to the action of water waves, and this constitutes an interesting hydroelastic problem, especially in variable bathymetry regions and in areas of intermediate and shallow water depth. The case of very large floating structures (VLFS) and megafloats are examples of structures for which the above problems find important applications. Furthermore, the hydroelastic analysis of floating bodies is very relevant to problems concerning the interaction of water waves with ice sheets; see, e.g., the reviews presented by Kashiwagi (2000), Watanabe et al. (2004), Wang et al. (2008) and Wang and Tay (2011), and by Squire et al. (1995) and Squire (2008) in the case of wave–ice interaction. Also, a detailed description of numerical techniques and computer codes for VLFS analysis in constant depth is presented in Riggs et al. (2008).

Under the assumption of small wave amplitude and plate deflection, most of the studies focus on the case of harmonic wave excitation, which enables the calculation of the floating body response in the frequency domain. In this case, a particular line of work is based on the modal expansion technique, where the elastic deformation is deduced by the superposition of distinct modes of motion. The hydrodynamic forces are treated primarily through the employment of the Green function method or the eigenfunction expansion matching method; see, e.g. Wang and Meylan (2002) and Belibassakis and Athanassoulis (2005), where also a review is included on various methods and techniques. Another line of works concentrates on transient analysis of elastic floating bodies, allowing non-harmonic wave forcing and time-dependent loads on the body. These attempts incorporate direct time integration schemes, Fourier transforms, modal expansion techniques and other methods; see for e.g. Watanabe et al. (1998), Meylan and Sturova (2009) and Sturova (2009). Details concerning the development and application of the coupled mode method to treat the problem in the time domain and in the case of variable bathymetry regions are provided in Belibassakis and Athanassoulis (2006). For the time-dependent response of a heterogeneous elastic plate floating on shallow water of variable depth, Sturova (2008) has developed a method based on modal superposition. More recently, Papathanasiou et al. (2015) developed a higher-order finite element method for the time domain solution of the hydroelastic problem composed of a freely floating or semi-fixed body, while the nonlinear transient response is examined in Sturova et al. (2009) by a spectral-finite difference method.

Numerical methods for predicting the hydroelastic responses of VLFS in variable bathymetry regions have been proposed, based on BEM in conjunction with fast multipole techniques (Utsunomiya et al. 2001), and on eigenfunction expansions in conjunction with a step-like bottom approximation (Murai et al. 2003). In addition, Porter and Porter (2004) have derived an approximate, vertically-integrated, two-equation model for the problem of water-wave interaction with an ice sheet of variable thickness, lying over variable bathymetry, which is valid under mild-slope assumptions both with respect to the wetted surface of the ice sheet and the bottom boundary. In the case of the hydroelastic behaviour of large floating deformable bodies in general bathymetry, a new coupled-mode system has been derived and examined by Belibassakis and Athanassoulis (2005) based on a local vertical expansion of the wave potential in terms of hydroelastic eigenmodes, and extending previous similar approach for the propagation of water waves in variable bathymetry regions (Athanassoulis and Belibassakis 1999). Similar approaches with application to wave scattering by ice sheets of varying thickness have been presented by Bennets et al. (2007) based on multi-mode expansion. An alternative formulation is based on the mode superposition method, where the solution is expressed in terms of hydrodynamic deflection modes, defined by plate eigenmodes or tensor products of beam eigenmodes; see e.g. Newman (1994), Kyoung et al. (2005).

In the present work, the coupled-mode model developed by Belibassakis and Athanassoulis (2005) is extended and applied to the hydroelastic analysis of 3D large floating bodies of finite extent and shallow draft or ice sheets of small thickness, lying over variable bathymetry regions. A general bathymetry is assumed, characterized by a continuous depth function, joining two regions of constant, but possibly different, depth. Following previous works for the propagation and diffraction of water waves over 3D bathymetric terrains (Belibassakis et al. 2001; Gerostathis et al. 2008), we consider the scattering problem of harmonic, obliquely incident surface waves, under the combined effects of variable bathymetry and a floating elastic plate of orthogonal planform shape. Under the assumption of small-amplitude waves and small plate deflections, the hydroelastic problem is formulated within the context of linearized water-wave and thin elastic-plate theory. To consistently treat the wave field beneath the elastic floating plate, down to the sloping bottom boundary, a complete, local, hydroelastic-mode series expansion of the wave field is used, enhanced by an appropriate sloping-bottom mode. The latter enables the consistent satisfaction of the Neumann bottom-boundary condition on a general topography. First numerical results concerning floating structures lying over flat and inhomogeneous seabed are comparatively presented, and the effects of wave direction, bottom slope and bottom corrugations on the hydroelastic responses are discussed.

2 Formulation of the problem

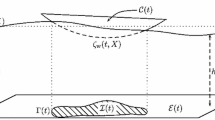
The studied environment consists of a water layer bounded above partly by the free surface and partly by a large floating elastic body that could be considered as a large shallow-draft platform or an ice sheet of small thickness, and below by a rigid bottom; see Fig. 1. It is also assumed that the bottom surface exhibits an arbitrary variation in a bounded subdomain, including into its interior the bottom inhomogeneity and the floating plate, which will act as a localized scatterer. Outside this area, the bathymetry is characterized by parallel, straight bottom contours lying between two regions of constant but different depth, $h=h_1$ (region of incidence, corresponding to $x<a_{1})$ and $h=h_3$ (region of transmission, corresponding to $x>a_{2})$. The horizontal plane is decomposed into the plate region (E) and the water region (W) outside the floating structure.

Fig. 1

Floating elastic body of length L and breadth B in the variable bathymetry region, modelled as thin plate

The wave field is excited by a monochromatic plane wave of angular frequency $\omega$, propagating with an oblique direction $\theta _1$ with respect to the bottom contours. A Cartesian coordinate system is introduced, with its origin at some point on the mean elastic-plate surface (in the variable bathymetry region) and the z-axis pointing upwards. The function $h=h( {x,y})$ represents the local depth, measured from the mean water level. In this work, we consider the scattering problem of harmonic, obliquely incident, surface (gravity) plane waves under the combined effects of variable bathymetry and the floating elastic plate of small thickness, modelling a shallow draft structure of orthogonal shape with length L and breadth B,  in the variable bathymetry region, as shown in Fig. 1. However, our analysis can be further extended to a floating elastic structure of more general shape. Under the usual assumptions of linearized water-wave theory and thin- (Kirchhoff) plate theory, the problem can be treated in the frequency domain. The wave potential is expressed in the following form:

$$\begin{aligned} \Phi ( {x,y,z\text {;}t})=\mathrm{Re}\left\{ {\varphi ( {x,y,z})\exp ( {-i\omega t})} \right\} , \end{aligned}$$

(1a)

where $i=\sqrt{-1}$. The complex amplitude of the free-surface elevation ($\eta$) is obtained in terms of the wave potential as follows:

$$\begin{aligned} \eta ( {x,y})=\frac{i}{\omega }\frac{\partial \varphi ( {x,y,z=0})}{\partial z}=\frac{i\omega }{g}\varphi ( {x,y,z=0}), \end{aligned}$$

(2a)

where g is the acceleration due to gravity. In the area of the elastic plate, the deflection (w) is connected with the wave potential by a similar relation derived from the kinematical condition at the liquid–solid interface,

$$\begin{aligned} w( {x,y})=\frac{i}{\omega }\frac{\partial \varphi ( {x,y,z=0})}{\partial \,z}. \end{aligned}$$

(2b)

The differential formulation of the studied problem consists of the Laplace equation in the water layer

$$\begin{aligned} ( {\nabla ^2 +\partial _z^2 })\varphi =0,\quad \text {in}\quad -h( {x,y})<z<0,\quad ( {x,y})\in W\cup E, \end{aligned}$$

(3a)

where $\nabla =( {\partial _x ,\partial _y })$ denotes the horizontal gradient operator. In the part of the horizontal plane associated with the free surface, the wave potential satisfies the linearized free-surface boundary condition

$$\begin{aligned} \partial _z \varphi -\mu \varphi =0,\quad \text { on}\quad z=0,( {x,y})\in W, \end{aligned}$$

(3b)

where $\mu =\omega ^2/g$ is the frequency parameter. Moreover, for points on the plate, the wave potential satisfies the corresponding dynamical equation forced by the water pressure

$$\begin{aligned} \nabla ^2( {d\nabla ^2w})+( {1-\varepsilon })w=\frac{i\mu }{\omega }\varphi ,\quad \text { on}\quad z=0,\quad ( {x,y})\in E,\nonumber \\ \end{aligned}$$

(3c)

where w is the plate deflection. The above equation is obtained by combining the thin elastic-plate equation with the linearized Bernoulli’s equation for the dynamic water pressure on the elastic-plate surface and involves the (constant) parameters $d=D/\rho g$ and $\varepsilon =m\omega ^2/\rho g$, where $D=Et^3/12( {1-\nu ^2})$ denotes the flexural rigidity of the elastic plate (the equivalent flexural rigidity of the platform), in which t denotes the possible variable thickness and $\nu$ the Poisson’s ratio. Moreover, $\rho$ denotes the fluid density and m is the mass per unit area of the plate.

In addition, at the plate edges, the following two conditions apply:

$$\begin{aligned} \frac{\partial ^3w}{\partial n^3}+( {2-\nu })\frac{\partial ^3w}{\partial n\,\partial s^2\,}=0,\quad \text { at}\quad ( {x,y})\in \partial W, \end{aligned}$$

(3d)

$$\begin{aligned} \frac{\partial ^2w}{\partial \,n^2}+\nu \frac{\partial ^2w}{\partial s^2}=0,\quad \text { at}\quad ( {x,y})\in \partial W, \end{aligned}$$

(3e)

where ${{\mathbf n}}$ and ${{\mathbf s}}$ denote the normal and tangential vectors, respectively. The above edge conditions state that the ends of the plate are free of shear force and moment, respectively.

Finally, at the sea bottom, the wave potential should satisfy the no-entrance boundary condition

$$\begin{aligned} \partial _z \varphi +\nabla h\nabla \varphi =0,\quad \text { on}\quad z=-h( {x,y}),\,( {x,y})\in W\cup E. \end{aligned}$$

(3f)

In the present work the above problem is solved by using appropriate vertical local-mode expansions of the wave potential, different in the water region and the fluid region under the elastic plate. The latter representations should match on the vertical interface separating these two subregions, as a consequence of momentum and mass conservation, respectively. This result is obtained under the smallness assumption concerning both the wave amplitude and the plate thickness leading to the linearization of both the free-surface boundary conditions (Eq. 3b) and the plate-boundary conditions (Eq. 3c) on the mean level ($z=0$).

3 Modal expansion of the wave potential

The studied problem, Eq. (3a, 3b, 3c, 3d, 3e, 3f), combines the character of water-wave propagation and scattering in inhomogeneous bathymetric terrains, under the additional effects due to the presence of localized hydroelastic scatterer (E). This type of problem has been extensively studied in a series of works by the authors, starting with the linearized water-wave problem in general bathymetry (Athanassoulis and Belibassakis 1999; Belibassakis et al. 2001), where the following local mode series expansion is used to consistently represent the wave field in the water region:

$$\begin{aligned} \varphi ( {{{\mathbf x}},z})= & {} \varphi _{-1} ( {{\mathbf x}})Z_{-1} ( {z;{{\mathbf x}}})+\sum \limits _{n=0}^\infty {\varphi _n ( {{\mathbf x}})} \,Z_n ( {z;{{\mathbf x}}}),\nonumber \\&-h( {{\mathbf x}})<z<0,\quad {{\mathbf x}}=( {x,y}). \end{aligned}$$

(4)

The major part of the set of vertical modes $\{ Z_n ( {z;{{\mathbf x}}}),\,n=0,$ $1,2,\ldots \}$ is dependent on ${{\mathbf x}}$ through $h( {{\mathbf x}})$ and is obtained as the solution of a vertical eigenvalue problem, formulated at each horizontal position. Moreover, $\varphi _{-1} ( {{\mathbf x}})\,Z_{-1} ( {z;{{\mathbf x}}})$ is an appropriate term, called the sloping-bottom mode, accounting for the satisfaction of the bottom boundary condition on the non-horizontal parts of the bottom. The idea of the sloping bottom mode, in conjunction with the above type of modal expansion, has been first introduced in the case of water waves propagating in variable bathymetry. Then, it has been used for many problems exhibiting similar features, such as nonlinear water waves (Athanassoulis and Belibassakis 2007; Belibassakis and Athanassoulis 2011), hydroacoustics (Athanassoulis et al. 2008; Belibassakis et al. 2014) and hydroelastic applications in variable bathymetry regions, formulated in the context of classical thin plate theory (Belibassakis and Athanassoulis 2005), including high-order extensions in the direction of shear deformable plate theory (Athanassoulis and Belibassakis 2009). In accordance with the latter works, the infinite set $Z_n ( {z;x}),\,n=0,1,2,3,\ldots$, of functions describing the vertical structure of each mode, at each horizontal position x, are generated by

$$\begin{aligned}&\partial _z^2 Z_n ( z)-\kappa _n^2 Z_n ( z)=0,\quad \text { in the vertical interval}\nonumber \\&\quad -h( {{\mathbf x}})<z<0, \end{aligned}$$

(5a)

$$\begin{aligned} \partial _z Z_n ( {z=-h})=0,\quad \text {at the bottom}\quad z=-h( {{\mathbf x}}), \end{aligned}$$

(5b)

$$\begin{aligned}&\alpha ( \kappa )\,\,\partial _z Z_n ( {z=0})-\mu \,Z_n ( {z=0})=0,\nonumber \\&\text { at the water}{\hbox {-}}\text {elastic body interface}\,z=0, \end{aligned}$$

(5c)

where $\alpha ( \kappa )$ is a function of $\kappa$ for hydroelastic waves and simplifies to $\alpha =1$ in the case of water waves. The solution of the above local vertical eigenvalue problem is given by

$$\begin{aligned} Z_n ( z)= & {} \mathrm{cosh}^{-1}( {\kappa _n \,h})\mathrm{cosh}\left[ {\kappa _n ( {z+h})} \right] ,\nonumber \\&\quad n=0,1,2,3,\ldots , \end{aligned}$$

(6)

where the eigenvalues $\{ {\kappa _{n} ,n=0,1,2\ldots }\}$ are obtained as the roots of the (local at any horizontal position ${{\mathbf x}})$ dispersion relation

$$\begin{aligned} \mu h=\alpha ( \kappa )\kappa h\tanh ( {\kappa h}), \end{aligned}$$

(7a)

with

$$\begin{aligned}&\alpha =1,\quad \text {for}\quad {{\mathbf x}}\in W,\quad \text {and}\quad \alpha ( \kappa )=d\,\kappa ^4h^4+1-\varepsilon ,\nonumber \\&\quad \text {for}\quad {{\mathbf x}}\in E. \end{aligned}$$

(7b)

Fig. 2

Distribution of the roots of the hydroelastic dispersion relation (Eq. 7a, 7b) on the complex $\kappa$-plane

The distribution of the roots ($\kappa _n^W$, for ${{\mathbf x}}\in W$ and $\kappa _n^E$, for ${{\mathbf x}}\in E)$ of the above dispersion relation on the complex $\kappa$-plane, which are used in the vertical structure, Eq. (6), of the expansion, Eq. (4), are schematically plotted in Fig. 2. For water waves, the first root is real and associated with the propagating mode, and the rest are imaginary associated with the evanescent modes. For hydroelastic waves, except for the previous categories, there exist also roots on the complex plane associated with modes characterized by mixed propagating–evanescent character. Except for the propagating and evanescent modes, the local mode expansion is augmented by the sloping bottom mode $\varphi _{-1} ( {{\mathbf x}})\,Z_{-1} ( {z;{{\mathbf x}}})$, permitting the consistent satisfaction of the Neumann boundary condition at the non-horizontal parts of the bottom surface and making the local mode series rapidly convergent. A specific convenient form of the vertical structure $Z_{-1} ( {z;h( {{\mathbf x}})})$ of this mode is given by low degree polynomials; however, other forms are also possible. More details concerning the role and significance of this term can be found in Athanassoulis and Belibassakis (1999) and Belibassakis et al. (2001).

4 Coupled-mode system of equations

The coupled-mode system (CMS) of horizontal differential equations is obtained with the aid of a variational principle developed by Belibassakis and Athanassoulis (2005), based on an energy-type functional of the form

$$\begin{aligned} {{\varvec{\mathscr {F}}}}( {\varphi ,w})= & {} \frac{\mu }{2}\int \limits _{{\mathbf x}} {\int \limits _{z=-h( {{\mathbf x}})}^{z=0} {( {\nabla \varphi })^2} } \,\mathrm{d}z\mathrm{d}{{\mathbf x}}+i\omega \mu \nonumber \\&\times \int \limits _{{\mathbf x}} {\varphi ( {{{\mathbf x}},z=0})\,w\,\mathrm{d}{{\mathbf x}}}-\frac{\omega ^2}{2} \nonumber \\&\times \int \limits _{{\mathbf x}} {\left( {\left( {d\nabla ^2w}\right) ^2+( {1-\varepsilon })\,w^2}\right) } \,\mathrm{d}{{\mathbf x}}+{{\varvec{\mathscr {F}}}}_a. \end{aligned}$$

(8a)

In the above equation, ${{\varvec{\mathscr {F}}}}_a$ are appropriate additional terms associated with the satisfaction of end-plate conditions, Eqs. (3d, 3e) at the borderline of the plate, and the boundary conditions concerning wave incidence in the far upwave region and outgoing wave at the radiation boundary. The variational principle is obtained by requiring the stationarity of the above functional:

$$\begin{aligned} \delta {{\varvec{\mathscr {F}}}}= & {} \int \limits _{{\mathbf x}} {\int \limits _{z=-h( {{\mathbf x}})}^{z=0} {\nabla ^2\varphi } } \delta \varphi \mathrm{d}z\mathrm{d}{{\mathbf x}}\nonumber \\&+\int \limits _{{\mathbf x}} {\left( {\frac{\partial \varphi }{\partial z}+\nabla h\nabla \varphi }\right) _{z=-h} \delta \varphi \,\mathrm{d}{{\mathbf x}}}\nonumber \\&-\int \limits _{{\mathbf x}} {\left( {\frac{\partial \varphi }{\partial z}+i\omega w}\right) _{z=0} \,\delta \varphi \,\mathrm{d}{{\mathbf x}}}\nonumber \\&+g\,\,\int \limits _{{\mathbf x}} {\bigg ( {\bigg ( {\nabla ^2d\nabla ^2w}\bigg )+( {1-\varepsilon })\,w-\frac{i\mu }{\omega }\,\varphi }\bigg )} \,\delta w\mathrm{d}{{\mathbf x}}\nonumber \\&+\delta {{\varvec{\mathscr {F}}}}_a =0. \end{aligned}$$

(8b)

The CMS is finally derived by using the representation of the local mode series expansion Eq. (4) of the wave potential, in the water column below the free surface and below the elastic plate, modelling the large elastic floating body. This permits us to reformulate the problem, Eq. (3a, 3b, 3c, 3d, 3e, 3f) with respect to the unknown modal amplitudes $\varphi _n ( {{\mathbf x}}),\,n=-1,0,1,2,\ldots ,$ for ${{\mathbf x}}\in W\cup E$. The present CMS takes the following form (Belibassakis and Athanassoulis 2005)

$$\begin{aligned}&\sum \limits _{n=-1}^\infty {a_{mn} ( {{\mathbf x}})\,\nabla ^2\,\varphi _n \,( {{\mathbf x}})+b_{mn} ( {{\mathbf x}})\nabla \,\varphi _n +c_{mn} ( {{\mathbf x}})} \varphi _n ( x)\nonumber \\&\quad =i\omega \,w( {{\mathbf x}})\cdot \chi (E),\quad m=-1,0,1,\ldots , \end{aligned}$$

(9a)

where $\chi (E)$ denotes the characteristic function of the plate subdomain E (i.e. $\chi ( E)=1,\,\text {for}\,{{\mathbf x}}\in E,$ $\,\text {and}\,0\,\text {otherwise})$. The system, Eq. (9a), is supplemented by the following equation completing the coupling between the modes $\varphi _n$ and the elastic-plate deflection w:

$$\begin{aligned} \nabla ^2( {d\nabla ^2w})+( {1-\varepsilon })w=\frac{i\mu }{\omega }\sum \limits _{n=-1}^\infty {\varphi _n ( {{\mathbf x}})}. \end{aligned}$$

(9b)

In the above equations, the horizontally dependent coefficients $a_{mn} ( {{\mathbf x}})\,$, $b_{mn} ( {{\mathbf x}})$ and $c_{mn} ( {{\mathbf x}})$ are given by the following expressions

$$\begin{aligned} a_{mn} ( {{\mathbf x}})=\langle {Z_n ,Z_m }\rangle , \end{aligned}$$

(10a)

$$\begin{aligned} b_{mn} ( {{\mathbf x}})=2\langle {\nabla Z_n ,Z_m } \rangle +\nabla \,h\,Z_n ( {z=-h})Z_m ( {z=-h}), \end{aligned}$$

(10b)

$$\begin{aligned}&c_{mn} ( {{\mathbf x}})=\langle {\nabla ^2Z_n +\partial _z^2 Z_n ,\,Z_m } \rangle \nonumber \\&\quad +\left( {\frac{\partial Z_n ( {z=-h})}{\partial \,z}+\nabla h\,\nabla Z_n ( {z=-h})\,}\right) \nonumber \\&\quad Z_m ( {z=-h}), \end{aligned}$$

(10c)

where $\langle {f,g} \rangle =\int \nolimits _{z=-h( {{\mathbf x}})}^{z=0} {f( z)g( z)\mathrm{d}z}$.

Furthermore, it is possible to eliminate the deflection w from the above system Eq. (9a, 9b) and derive an equivalent form. One way to succeed it is by using the kinematical condition on the plate surface Eq. (2b), in conjunction with the hydroelastic model expansion Eq. (4) to express the vertical derivative of the potential at the plate surface as follows:

$$\begin{aligned} w( {x,y})= & {} \frac{i}{\omega }\frac{\partial \varphi ( {x,y,z=0})}{\partial \,z}=\frac{i}{\omega }\sum \limits _n {\varphi _n } \frac{\partial Z_n ( {x,y,z=0})}{\partial \,z}\\= & {} \frac{i}{\omega }\sum \limits _n \varphi _n{\kappa _n } \tanh ( {\kappa _n h}). \end{aligned}$$

In this case, the present CMS takes the following equivalent form:

Fig. 3

Comparison between the present method (solid lines) and experimental data from Wu et al. (1995), concerning the plate deflection modulus. Waves of period $T=2.875$ s (squares), $T=1.429$ s (triangles) and $T=0.7$ s (circles), normally incident on a floating elastic plate of aspect ratio 20, lying over a flat bottom in a water layer of depth $h=1.1$ m

Fig. 4

a Geometrical configuration. b Effect of bathymetric variations on the wave field and the elastic-plate deflection, in the case of waves of period $T=15$ s normally incident on a large floating structure over the smooth shoal, as calculated by the present method. The PML region is located outside the region indicated using dashed lines

$$\begin{aligned}&\sum \limits _{n=-1}^\infty \Big \{ a_{mn} ( {{\mathbf x}})\,\nabla ^4\varphi _n +\,{{\mathbf b}}_{mn} ( {{\mathbf x}})\nabla ^3\,\varphi _n \nonumber \\&\quad +\left[ {c_{mn}^{( 1)} ( {{\mathbf x}})+c_{mn}^{( 2)} ( {{\mathbf x}})} \right] \nabla ^2\,\varphi _n +\left[ {{{\mathbf d}}_{mn}^{( 1)} ( {{\mathbf x}})+{{\mathbf d}}_{mn}^{( 2)} ( {{\mathbf x}})} \right] \nabla \,\varphi _n \, \nonumber \\&\quad +\left[ {e_{mn}^{( 1)} ( {{\mathbf x}})+e_{mn}^{( 2)} ( {{\mathbf x}})} \right] \,\varphi _n ( x) \Big \}=0,\quad m=-1,0,1,\ldots . \end{aligned}$$

(11)

In the above equations, the horizontally dependent coefficients $a_{mn} ( {{\mathbf x}})$, ${{\mathbf b}}_{mn} ( {{\mathbf x}})$, $c_{mn}^{( 1)} ( {{\mathbf x}})$, $c_{mn}^{( 2)} ( {{\mathbf x}})$, ${{\mathbf d}}_{mn}^{( 1)} ( {{\mathbf x}})$, ${{\mathbf d}}_{mn}^{( 2)} ( {{\mathbf x}})$, $e_{mn}^{( 1)} ( {{\mathbf x}})$, $e_{mn}^{( 2)} ( {{\mathbf x}})$ are given by the following expressions:

$$\begin{aligned} a_{mn} ( {{\mathbf x}})\,=\left\{ {{\begin{array}{ll} {-d\,\partial _z Z_n ( {z=0})\partial _z Z_m ( {z=0}),} &{}\quad {{{\mathbf x}}\in E}\\ {0,} &{}\quad {{{\mathbf x}}\in W} \\ \end{array} }} \right. , \end{aligned}$$

(12a)

$$\begin{aligned} {{\mathbf b}}_{mn} ( {{\mathbf x}})=\left\{ {{\begin{array}{ll} {\left[ {-4d\,\nabla ( {\partial _z Z_n (z=0)})-2\partial _z Z_n (z=0)\nabla d} \right] \partial _z Z_m (z=0),} &{}\quad {{{\mathbf x}}\in E} \\ {0,} &{}\quad {{{\mathbf x}}\in W} \\ \end{array} }} \right. , \end{aligned}$$

(12b)

$$\begin{aligned} c_{mn}^{( 1)} ( {{\mathbf x}})=\left\{ {{\begin{array}{ll} {\left[ {-6d\nabla ^2( {\partial _z Z_n (z=0)})-6\nabla d\cdot \nabla ( {\partial _z Z_n (z=0)})} \right. } &{}\quad \\ {\left. {\quad -\nabla ^2d\,\partial _z Z_n (z=0)} \right] \partial _z Z_m (z=0),} &{}\quad {{{\mathbf x}}\in E} \\ {0,} &{}\quad {{{\mathbf x}}\in W} \\ \end{array} }} \right. , \end{aligned}$$

(12c)

$$\begin{aligned} c_{mn}^{( 2)} ( {{\mathbf x}})=\mu \left\langle {Z_n ,Z_m } \right\rangle ,\quad {{\mathbf x}}\in W\cup E, \end{aligned}$$

(12d)

$$\begin{aligned} {{\mathbf d}}_{mn}^{( 1)} ( {{\mathbf x}})=\left\{ {{\begin{array}{ll} {\left[ {-4d\nabla ^3( {\partial _z Z_n (z=0)})-2\nabla ^2d\,\nabla ( {\partial _z Z_n (z=0)})+} \right. } &{}\quad \\ {\left. {\quad -6\nabla d\nabla ^2( {\partial _z Z_n (z=0)})} \right] \partial _z Z_m (z=0),} &{}\quad {{{\mathbf x}}\in E} \\ {0,} &{}\quad {{{\mathbf x}}\in W} \\ \end{array} }} \right. , \end{aligned}$$

(12e)

$$\begin{aligned} {{\mathbf d}}_{mn}^{( 2)} ( {{\mathbf x}})=\mu \left[ {2\left\langle {\nabla Z_n ,Z_m } \right\rangle +\nabla h\,Z_n ( {z=-h( {{\mathbf x}})})Z_m ( {z=-h( {{\mathbf x}})})} \right] ,\quad {{\mathbf x}}\in W\cup E, \end{aligned}$$

(12f)

$$\begin{aligned} e_{mn}^{( 1)} ( {{\mathbf x}})=\left\{ {{\begin{array}{ll} {\left[ {-d\,\nabla ^4( {\partial _z Z_n (z=0)})-2\nabla d\,\nabla ^3( {\partial _z Z_n (z=0)})-\nabla ^2d\,\nabla ^2( {\partial _z Z_n (z=0)})+} \right. } &{}\quad \\ {\left. {\quad -( {1-\varepsilon })\partial _z Z_n (z=0)+\mu Z_n (z=0)} \right] \partial _z Z_m (z=0),} &{}\quad {{{\mathbf x}}\in E} \\ {0,} &{}\quad {{{\mathbf x}}\in W} \\ \end{array} }} \right. , \end{aligned}$$

(12g)

$$\begin{aligned} e_{mn}^{( 2)} ( {{\mathbf x}})=\mu \,[ {\langle {\nabla ^2Z_n +\partial _z^2 Z_n ,\,Z_m } \rangle +\nabla h\,\,\nabla Z_n ( {z=-h( {{\mathbf x}})})Z_m ( {z=-h})\,} ],\quad {{\mathbf x}}\in W\cup E. \end{aligned}$$

(12h)

After solving the present CMS, the wave characteristics can be obtained all over the domain by means of the calculated wave modes $\varphi _n ( x),n=-1,0,1,2,3,\ldots$, using the expansion Eq. (4). Finally, information concerning distributions of moments and stresses on the plate is obtained from the solution, through the vertical deflection w; see also Belibassakis and Athanassoulis (2005).

Fig. 5

a Distribution of deflection for an elastic plate over a shoal (maximum bottom slope 10 %), normalized with respect to the incident wave height. The wave incidence is normal. b Plate deflection along the longitudinal and transverse cuts shown in a, normalized with respect to the incident wave height

5 Setup of the discrete system

The present CMS is solved, using appropriate boundary conditions specifying the wave incidence (see Fig. 1) and the boundary conditions Eq. (3d) and (3e) associated with elastic-plate deflection at the edges, enforcing zero shear force and moment. The discrete version of the present hydroelastic CMS is obtained by truncating the local-mode series Eq. (4) to a finite number of terms (modes), and using central, second-order finite differences to approximate the horizontal derivatives. Discrete boundary conditions for both the incident wave and the deflection at the plate edges are obtained by using second-order forward and backward differences to approximate the horizontal derivatives. Using the present local mode representations, the continuity of the potential and its normal derivative on the vertical interface separating the water subregion from the fluid region under the plate is satisfied by

$$\begin{aligned}&\sum \limits _{n=-1}^\infty \left( \varphi _n \left( {{{\mathbf x}}-\varepsilon _*{{\mathbf n}}}\right) Z_n \left( {{{\mathbf x}}-\varepsilon _*{{\mathbf n}}}\right) -\varphi _n \left( {{{\mathbf x}}+\varepsilon _*{{\mathbf n}}}\right) \right. \nonumber \\&\quad \times \left. Z_n \left( {{{\mathbf x}}+\varepsilon _*{{\mathbf n}}}\right) \right) =0, \end{aligned}$$

(13a)

$$\begin{aligned}&\sum \limits _{n=-1}^\infty {{\mathbf n}}\nabla ( \varphi _n ( {{{\mathbf x}}-\varepsilon _*{{\mathbf n}}})Z_n ( {{{\mathbf x}}-\varepsilon _*{{\mathbf n}}})\nonumber \\&\quad -\varphi _n ( {{{\mathbf x}}+\varepsilon _*{{\mathbf n}}})Z_n ( {{{\mathbf x}}+\varepsilon _*{{\mathbf n}}})) \,=0, \end{aligned}$$

(13b)

where n denotes the normal vector (on the horizontal plane) along the borderline of the plate and $\varepsilon _*$ is small and positive. In this respect, double nodes are introduced for the wave potential along the borderline of the plate, and the continuity of the potential is satisfied by projecting the above equation on the vertical basis $\{ {Z_m ( {{{\mathbf x}}-\varepsilon _*{{\mathbf n}}}),\,m=-1,0,1\ldots }\},\,{{\mathbf x}}\in \partial E$. Also, forward and backward differences have been used to express the normal derivatives appearing in Eq. (13b) of the potential in the water subregion and in the plate subregion, respectively.

Fig. 6

Wave field for plate with size aspect ratio $L/B=2$. a Normal incidence, $\theta _1 =0^{\circ }$, b oblique incidence, $\theta _1 =15^{\circ }$, c oblique incidence, $\theta _1 =30^{\circ }$

Fig. 7

Effect of the incident wave angle on the modulus of the plate deflection for an elastic plate over a shoal (maximum bottom slope 10 %) along various cuts as shown in Fig. 5a. The three incidence angles examined are: (i) normal incidence, $\theta _1 =0^{\circ }$ (solid line), (ii) oblique incidence, $\theta _1 =15^{\circ }$ (dashed line) and (iii) very oblique incidence, $\theta _1 =30^{\circ }$ (dashed dot line)

Furthermore, the present model is applied to the solution of the studied problem, in conjunction with the perfectly matched layer (see Collino and Monk 1998). The latter PML permits truncation of the computational domain on the horizontal plane, and its coefficients are optimized as discussed in Belibassakis et al. (2001) for absorbing the propagating and scattered waves arriving at the lateral and downwave boundaries of the domain with minimum reflection. In particular, in the area of the absorbing layer of uniform thickness l, surrounding the horizontal computational domain in the water subregion, and assuming that the coefficient matrix $a_{mn}$ is non-singular, the present CMS takes the form

$$\begin{aligned}&\sum \limits _{n=-1}^\infty {\delta _{mn} \,\nabla ^2\varphi _n \,( {x,y})} +( {a_{mn}})^{-1}\nonumber \\&\quad \times \left[ {{{\varvec{b}}}_{mn} ( {x,y})\,\cdot \nabla \varphi _n ( {x,y})+c_{mn} \;\varphi _n ( {x,y})} \right] =0,\nonumber \\&\quad m=-1,0,1,\ldots . \end{aligned}$$

(14)

Since the wavelike behaviour of the system for $\varphi _n$ is essentially determined by the propagating ($n=0$) mode, a straightforward approach is to substitute, at the next step, the horizontal Laplacian operator appearing in Eq. (14) by the PML operator, defined as follows:

$$\begin{aligned} {\varvec{{\mathscr {D}}}}^2\varphi _n =\left\{ {{\begin{array}{l@{\quad }l} \frac{1}{s_x }\left( {\frac{\partial }{\partial x}\left( {\frac{1}{s_x }\frac{\partial \varphi _n }{\partial x}}\right) }\right) +\frac{1}{s_y }\left( {\frac{\partial }{\partial y}\left( {\frac{1}{s_y }\frac{\partial \varphi _n }{\partial y}}\right) }\right) ,&{} n=0 \\ \nabla ^2\varphi _n ,&{} n\ne 0 \\ \end{array} }} \right. ,\nonumber \\ \end{aligned}$$

(15a)

where the PML-coefficients are defined by

$$\begin{aligned} s_x =1+\frac{i\sigma ( {\tilde{x}})}{k}\quad \text {and}\quad s_y =1+\frac{i\sigma ( {\tilde{y}})}{k}. \end{aligned}$$

(15b)

In the above equation $\tilde{x}$,$\tilde{y}$ are scaled variables starting at the interior boundary of the PML, and the function $\sigma$ is positive and defined by

$$\begin{aligned}&\sigma ( {\tilde{x}})=\sigma _0 ( {\tilde{x}/l})^n,\quad \sigma ( {\tilde{x}})=\sigma _0 ( {\tilde{x}/l})^n,\quad n\ge 3,\nonumber \\&\quad \text { in the PML and zero elsewhere}. \end{aligned}$$

(15c)

The optimum values for $\sigma _0$ and n coefficients and more details about the present version of the PML can be found in Belibassakis et al. (2001) where it was first implemented in conjunction with the present coupled-mode system for water waves over 3D variable bathymetric terrains. The drawback of the PML model is that a layer surrounding the computational domain of width approximately equal to the local wavelength is sacrificed for enforcing the absorbing condition. The same method has been applied very successfully for similar problems in the additional presence of scattering by other sources, as for example in the case of inhomogeneous currents in variable bathymetry regions, as presented in Belibassakis et al. (2011). Thus, the discrete scheme obtained is uniformly of second order in the horizontal direction. The coefficient matrix of the discrete system is block structured with five- and seven-diagonal blocks, corresponding to the discrete version of the CMS. The system is numerically constructed and solved by means of a parallel implementation, making feasible the treatment of realistic domains corresponding to areas with size of the order of many characteristic wavelengths.

Finally, for the treatment of the weak singularities in the vicinity of the corners, in the case of orthogonal elastic floating bodies, like the examples considered in this work, a regularizing scheme has been applied to the boundary conditions necessitating zero shear and moment at the border of the plate, as well as to the interface conditions, necessitating continuity of normal derivative of the potential. In this respect, all normal and tangential derivatives at the corner points are approximated in the discrete scheme by averages of the same quantities at the next (nearby) nodes at each side of the corner.

6 Numerical results and discussion

6.1 Elastic plate in constant depth

For the validation of the present method, in this section, numerical results are presented using data concerning the physical parameters from the experiment by Wu et al. (1995). In this case, the length of the model was $L=10$ m, its breadth $B=0.5$ m, its thickness 0.038 m and the elastic modulus of the material $E=103\,\mathrm{MPa}$. Moreover, the model density was $\rho _p =220\,\mathrm{kg}/{\mathrm{m}^3}$, and thus its draft $d=0.0084$ m. The experiment was performed in a water depth of $h=1.1$ m, using incident wave heights of 5, 10 and 20 mm and wave periods ranging from 0.5 to 3 s, corresponding to deep and intermediate water depth conditions, respectively.

Fig. 8

Wave field for normal incidence, $\theta _1 =0^{\circ }$. a Plate size aspect ratio $L/B=1$, b plate size aspect ratio $L/B=2$ and c plate size aspect ratio $L/B=4,$ respectively

In Fig. 3, the comparison between the present method (solid lines) and the experimental data (circles) concerning the modulus of the plate deflection is shown, normalized with respect to the wave amplitude. More specifically, harmonic waves of period $T=2.875$, 1.429 and 0.7 s, respectively, normally incident on a floating elastic plate of aspect ratio 20 are considered. In all cases, the present method results are found to be in very good agreement with measured data.

Fig. 9

a Geometrical configuration. b Effect of bathymetric variations on the wave field and the elastic-plate deflection, in the case of waves of period $T=15$ s normally incident on a large floating structure over the smooth undulating bottom, as calculated by the present method. The PML region is indicated using dashed lines

6.2 Elastic plate over smooth underwater shoal

To illustrate the effects of variable bathymetry (sloping bottom) on the hydroelastic behaviour of the system as modelled by the present method, as a first example we consider in Fig. 4 a large elastic floating body ($L=240$ m, $B=120$ m) modelled as a thin elastic plate, with constant characteristics $d=10^{5}$ m$^{4}$, $\varepsilon =0.005$ and Poisson’s ratio $\nu =0.3$. This floating body lays over a smooth underwater shoal, characterized by a depth function smoothly varying from $h=15$ m to $h=5$ m over a distance of 1.5 km, as also shown in Fig. 4. The bathymetry is given analytically as follows,

$$\begin{aligned}&h( {x,y}){=}\frac{h_1 +h_3 }{2}{-}\frac{h_1 -h_3 }{2}\tanh \left( {\frac{\pi }{3}\left( {\frac{x-c_1 }{c_2 -c_1 }}\right) -\frac{1}{2}}\right) ,\nonumber \\&\quad ( {x,y})\in \left[ {a_1 ,a_2 } \right] \times \left[ {b_1 ,b_2 } \right] ,\nonumber \\ \end{aligned}$$

(16)

where $[ {a_1 ,a_2 } ]\times [ {b_1 ,b_2 } ]$ is the computational domain on the horizontal plane, with $a_1 =0$, $a_2 =1500$ m, $b_1 =-600$ m, $b_2 =600$ m the horizontal dimensions of the fluid domain, and the mean and maximum slopes are 1 and 10 %, respectively. The elastic plate is located in the middle of the variable bathymetry region and has dimensions $[ {c_1 ,c_2 } ]\times [ {d_1 ,d_2 } ]$, with $c_1 =550$ m, $c_2 =790$ m, $d_1 =-60$ m and $d_2 =60$ m, and thus the aspect ratio is $L/B=2$. The effect of bathymetric variations and the elastic-plate deflection on the calculated wave field, in the case of harmonic waves of period $T=15$ s that are normally incident on the elastic structure over the above smooth shoal, is presented in Fig. 4b. The calculations are based on a grid of 1201 $\times$ 961 points on the horizontal domain that is found enough for numerical convergence of the results. The detailed investigation of the present CMS in (Belibassakis and Athanassoulis 2005, Fig. 9) has revealed that the propagating mode ($n=0$) and the first two propagating–evanescent modes ($n=1,2$) are the most important, being one order of magnitude greater than the sloping-bottom mode ($n=-1$) and the next evanescent modes ($n=4,5$). The rest of the sequence of evanescent modes presents a fast rate of decay of the order $O( {n^{-4}})$ as n tends to infinity. Based on this remark and taking into account the huge computational cost in realistic three-dimensional applications in this work, the numerical results presented below are obtained by maintaining only the first three modes ($n=0,1,2$) in the hydroelastic expansion, Eq. (4).

Fig. 10

Variations on the wave field and the elastic-plate deflection a for flat bottom and b undulating bottom with $A_b =0.15h$ and c for undulating bottom with $A_b =0.30h$. Areas with significant changes are indicated using dashed areas

We observe in Fig. 4 the strong diffraction pattern generated by the elastic plate, especially in the front area of the plate where the reflection phenomena are dominant, as predicted by the present method. For comparative illustration of the 3D effects, in Fig. 5, the deflection modulus is plotted along various longitudinal and transverse sections of the plate, where we observe that elastic deformation is maximized at the upwave edges of the plate near the corners, as naturally expected.

Next, the effect of the incident wave angle on the modulus of the plate deflection for an elastic plate over the shoal with maximum bottom slope 10 % is illustrated in Fig. 6 for the same, as before, floating elastic plate, as calculated by the present CMS. Except normal wave incidence $\theta _1 =0^{\circ }$, also oblique waves have been considered $\theta _1 =15^{\circ }$ and $\theta _1 =30^{\circ }$. We clearly observe in Fig. 6 the effect on the diffraction pattern and the formation of the shadow zone downwave the plate.

Fig. 11

Effect of bottom corrugations on the modulus of the elastic-plate deflection. The three bottom profiles examined are: a horizontal bottom $A_b =0$, b undulating bottom with amplitude $A_b =0.1h$, c undulating bottom with amplitude $A_b =0.3h$, d distribution of deflection along all longitudinal and transverse sections shown in Fig. 5a for the same amplitudes. Results of the horizontal bottom are indicated with solid line, for $A_b =0.1h$ with dashed line and for $A_b =0.3h$ with dashed-dot line

Fig. 12

Effect of wave direction on the modulus of the elastic-plate deflection in the area with bottom corrugations of Fig. 9. a Normal incidence, $\theta _1 =0^{\circ }$, b oblique incidence, $\theta _1 =15^{\circ }$, c oblique incidence, $\theta _1 =30^{\circ }$, d distribution of deflection along all longitudinal and transverse sections shown in Fig. 5a, for the same angles of wave incidence as in a–b. Results for $\theta _1 =0^{\circ }$ are indicated with solid line, for $\theta _1 =15^{\circ }$ with dashed line and for $\theta _1 =30^{\circ }$ with dashed-dot line

To illustrate the corresponding effects of the wave direction on the plate deflection, in Fig. 7, the patterns of the deflection modulus are presented, along with the corresponding transverse and longitudinal sectional distributions. As expected, as the wave direction becomes more oblique, the elastic deformation in the plate area near the corner directly exposed to the incident wave energy becomes significantly increased, and the three-dimensional effects, especially asymmetry, due to the wave directionality are evident.

Next, in Fig. 8, the effect of the plate aspect ratio on the hydroelastic wave field is examined. In comparison to the previous plate of aspect ratio $L/B=2$, a shorter and a longer plate of aspect ratio $L/B=1$ and $L/B=4$, respectively, are used for comparative calculations by the present method. We observe that the modifications in the diffraction pattern are significant, and especially concerning the reflection of wave energy in the upwave region of the plate. In particular, the shorter plate shown in Fig. 6a is less elastically deformed in this excitation frequency, since the elastic wavelength is much larger than the plate length and the incident wavelength and, thus, it behaves as a more stiff and reflecting obstacle, in comparison with the longer plate plotted in Fig. 8c.

6.3 Elastic plate over smooth undulating bottom

To demonstrate the effects of bottom corrugations on the hydroelastic behaviour of the system, we examine the same configuration (elastic plate $L=240$ m, $B=120$ m, $d=10^5\,\mathrm{m}^4$, $\varepsilon =0$), lying over a smooth undulating bathymetry. In this case, the bottom profile is given by the following depth function,

$$\begin{aligned}&h( {x,y})=\nonumber \\&\left\{ {{\begin{array}{l@{\quad }l} h-g( x)A_b \sin ( {k_b ( {x-x_a })}),&{}( {x,y})\in \left[ {x_a ,x_b } \right] \times \left[ {b_1 ,b_2 } \right] \\ h,&{} ( {x,y})\in \left[ {a_1 ,x_a } \right) \times \left[ {b_1 ,b_2 } \right] \cup \left( {x_b ,a_2 } \right] \times \left[ {b_1 ,b_2 } \right] \\ \end{array} }} \right. , \end{aligned}$$

(17)

where $k_b =2\pi /\lambda _b$ is the bottom surface wave number, selected so that the corresponding bottom surface wave length $\lambda _b$ is equal to 0.25L. Moreover, $h=10$ m is the mean depth, and $A_b =0.15h$ is the amplitude of bottom undulations. The computational domain is $[ {a_1 ,a_2 } ]\times [ {b_1 ,b_2 } ]$, with $a_1 =0$, $a_2 =1500$ m, $b_1 =-600$ m, $b_2 =600$ m, and the horizontal dimensions and position of the elastic floating body inside the computational domain: $[ {c_1 ,c_2 } ]\times [ {d_1 ,d_2 } ]$, with $c_1 =550$ m, $c_2 =c_1 +L$, $d_1 =-60$ m and $d_2 =60$ m. Finally, the area of bottom undulations is enclosed in the subregion $[ {x_a ,x_b } ]\times [ {b_1 ,b_2 } ]$, with $x_a =c_1 -L$ and $x_a =c_2 +L$. To this aim, the function g( x)in Eq. (17) is a filter function defined by

$$\begin{aligned} g( x)= & {} \left( {1-\exp \left( {-\left( {\frac{x-x_a }{\lambda _b }}\right) ^2}\right) }\right) \nonumber \\&\times \left( {1-\exp \left( {-\left( {\frac{x-x_b }{\lambda _b }}\right) ^2}\right) }\right) , \end{aligned}$$

(18)

which is used to restrict the sea bottom corrugations in the middle of the computational domain. Thus, again the variable bathymetry subregion lies between two horizontal flat subregions, both of 10 m depth. For this example, the calculated wave field for normally incident harmonic waves of period $T=15$ s is presented in Fig. 9, as calculated by the present method using the same discretization corresponding to a horizontal grid of 1201 $\times$ 961 points on the horizontal domain that is again found enough for numerical convergence of the results.

Next, the effect of bottom slope and curvature on the calculated wave field and the elastic-plate deflection is investigated with the aid of Figs. 10 and 11. In particular, in Fig. 10, numerical results are presented for an undulating bottom with amplitude of bottom corrugations $A_b =0.15h$ and $A_b =0.30h$, respectively, and compared against the same structure floating above the flat horizontal bottom of the same mean depth $h=10$ m. Subareas where the diffraction patterns present significant changes are indicated in Fig. 10 using dashed lines. The effect of bottom corrugations on the modulus of the elastic-plate deflection is illustrated in Fig. 11, where distributions along the various longitudinal and transverse sections (defined in Fig. 5a) are comparatively plotted. We observe in this figure that, as bottom corrugations become stronger, significant changes in the elastic field pattern on the plate are produced, substantially increasing the deflection. This is due to the fact that bottom undulations could excite Bragg scattering, enhancing the backscattered wave energy in the region. This could lead to formation of partially standing waves in the area of the elastic floating structure, enhancing the energy interacting with the plate and finally increasing substantially the corresponding deflections, as illustrated in this example; see, e.g. last subplot of Fig. 11c. This finding could be important in various further directions and applications, e.g. in the design and analysis of mooring systems for large floating elastic structures or the investigation of such systems for wave power absorption; see e.g. Karmakar and Guedes Soares (2012) and Khabakhpasheva and Korobkin (2002).

Finally, in Fig. 12, the effect of the incident wave angle on the modulus of the plate deflection for an elastic plate floating over a variable bathymetry region is examined, by means of the present CMS. In this case, the same as before, a floating elastic structure is considered in the environment with bottom undulations as shown in Fig. 9. Again, we observe in Fig. 12 that as the incident waves becomes more oblique, the elastic deformation in the plate area near the corner directly exposed to the incident wave energy is significantly increased, and the three-dimensional effects, especially asymmetry of the plate deflection, due to the wave directionality becomes important.

7 Conclusions

In this work, the coupled-mode model developed by Belibassakis and Athanassoulis (2005) is extended and applied to the hydroelastic analysis of three-dimensional, large floating bodies of shallow draft lying over variable bathymetry regions. The present formulation finds also useful applications to the study of interaction of water waves with ice floes in coastal waters. A general bathymetry is assumed, characterized by a continuous depth function, joining two regions of constant, but possibly different, depth. Following previous works for the propagation and diffraction of water waves over general bathymetric terrains and in the presence of other inhomogenities, we consider the scattering problem of harmonic incident waves, under the combined effects of variable bathymetry and a large floating elastic structure of orthogonal planform shape. The hydroelastic problem is formulated within the context of linearized water-wave and thin elastic-plate theory. To treat the wave field beneath the elastic floating plate, down to the sloping bottom boundary, a complete, local, hydroelastic-mode series expansion of the wave field is used, enhanced by an appropriate sloping-bottom mode. The latter enables the consistent satisfaction of the Neumann bottom-boundary condition on a general topography and accelerates the convergence. Numerical results concerning floating structures over sloping and corrugated seabeds are shown, and the effects of wave direction, bottom slope and curvature on the hydroelastic responses are discussed. Future work is planned towards the investigation of hydroelastic responses of large floating bodies and structures of more general planform shape in variable bathymetry regions, as well as extensions to incorporate shear effects.