$H_\infty$ tracking adaptive fuzzy integral sliding mode control for a train of self-balancing vehicles

Abstract

A series of self-balancing vehicles is stabilized and controlled in this research work. The system is composed of several Segway $\frac{{\mathrm{TM}}}{}$ type platforms interconnected through flexible links. The system is inherently highly nonlinear and underactuated which makes the tracking task very challenging. In this paper, $H_\infty$ tracking adaptive fuzzy integral sliding mode control scheme is proposed for n-self-balancing interconnected vehicles system where uncertainties and disturbances are included. First, a nonlinear dynamic model with uncertainties for the train system with n-vehicles is derived using the Lagrangian method assuming the vehicles moving in tandem on a inclined path. Then, the dynamics of the train system with n-vehicles is formulated as an error dynamics according to a specified reference signal. A fuzzy technique with an on-line estimation scheme is developed to approximate the dynamics of the train system with n-vehicles. The advantage of employing an adaptive fuzzy system is the use of linear analytical results instead of estimating nonlinear uncertain functions in dynamics with an online update law. Using the concept of parallel distributed compensation, the adaptive fuzzy scheme combined with the integral sliding mode control scheme is synthesized to address the system uncertainties and the external disturbances such that $H_\infty$ tracking performance is achieved. Simulation results for 2-self-balancing interconnected vehicles system are presented to show the effectiveness and performance of the proposed control scheme.

Appendices

Appendix A Dynamic Model for the Self-Balancing-Train System with 2-Vehicles

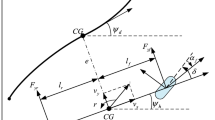
From Fig. 5 and (5), the following is obtained:

$$\begin{aligned} \ddot{\mathbf{q}}+\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})\dot{\mathbf{q}}+\mathbf{G}(\mathbf{q})+\mathbf{K}(\mathbf{q})\mathbf{q}=\mathbf{B}(\mathbf{q})\mathbf{u}+\mathbf{d}+\Delta \mathbf{f}\end{aligned}$$

(42)

where $\mathbf{q}=[\theta _{w_{_{1}}}\ \theta _{w_{_{2}}}\ \psi _{c_{_{1}}}\ \psi _{c_{_{2}}}]^\top$ is the vector for the generalized coordinates of the free system for which $\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})=\mathbf{H}_{_{0}}(\mathbf{q})^{-1}\mathbf{C}_{_{0}}(\mathbf{q},\dot{\mathbf{q}})$, $\mathbf{G}(\mathbf{q})=\mathbf{H}_{_{0}}(\mathbf{q})^{-1}\mathbf{G}_{_{0}}(\mathbf{q})$, $\mathbf{K}(\mathbf{q})=\mathbf{H}_{_{0}}(\mathbf{q})^{-1}\mathbf{K}'$, $\mathbf{B}(\mathbf{q})=\mathbf{H}_{_{0}}(\mathbf{q})^{-1}$, $\mathbf{d}=\mathbf{H}_{_{0}}(\mathbf{q})^{-1}\mathbf{d}'$, and $\Delta \mathbf{f}=\mathbf{H}_{_{0}}(\mathbf{q})^{-1}\big (\Delta \mathbf{H}(\mathbf{q})\ddot{\mathbf{q}}+\Delta \mathbf{C}(\mathbf{q},\dot{\mathbf{q}})\dot{\mathbf{q}}+\Delta \mathbf{G}(\mathbf{q})\big )$. Then $\mathbf{H}_{_{0}}(\mathbf{q})$ is the inertia matrix defined as follows:

$$\begin{aligned} \mathbf{H}_{_{0}}(\mathbf{q})=\left[ \begin{array}{cccc}h_{_{11}} &{} 0 &{} h_{_{13}} &{} 0 \\ 0 &{} h_{_{22}} &{} 0 &{} h_{_{24}}\\ h_{_{31}} &{} 0 &{} h_{_{33}} &{} 0\\ 0 &{} h_{_{42}} &{} 0 &{} h_{_{44}}\end{array}\right] \end{aligned}$$

(43)

where $h_{_{11}}=2J_{w_{_{1}}}+M_{c_{_{1}}}r^{2}_{_{w}}+2M_{w_{_{1}}}r^{2}_{_{w}}+2J_{m_{_{1}}}\eta ^2$, $h_{_{13}}=-2J_{m_{_{1}}}\eta ^2+LM_{c_{_{1}}}r_{_{w}}\cos (\alpha +\delta _{c_{_{1}}}+\psi _{c_{_{1}}})\cos (\alpha )$, $h_{_{22}}=2J_{w_{_{2}}}+M_{c_{_{2}}}r^{2}_{_{w}}+2M_{w_{_{2}}}r^{2}_{_{w}}+2J_{m_{_{2}}}\eta ^2$, $h_{_{24}}=-2J_{m_{_{2}}}\eta ^2+LM_{c_{_{2}}}r_{_{w}}\cos (\alpha +\delta _{c_{_{2}}}+\psi _{c_{_{2}}})\cos (\alpha )$, $h_{_{31}}=-2J_{m_{_{1}}}\eta ^2+LM_{c_{_{1}}}r_{_{w}}\cos (\alpha +\delta _{c_{_{1}}}+\psi _{c_{_{1}}})\cos (\alpha )$, $h_{_{33}}=J_{c_{_{1}}}+2J_{m_{_{1}}}\eta ^{2}+L^2M_{c_{_{1}}}\cos ^{2}(\alpha )$, $h_{_{42}}=-2J_{m_{_{2}}}\eta ^2+LM_{c_{_{2}}}r_{_{w}}\cos (\alpha +\delta _{c_{_{2}}}+\psi _{c_{_{2}}})\cos (\alpha )$, $h_{_{44}}=J_{c_{_{2}}}+2J_{m_{_{2}}}\eta ^{2}+L^2M_{c_{_{2}}}\cos ^{2}(\alpha )$, and $\mathbf{C}_{_{0}}(\mathbf{q},\dot{\mathbf{q}})$ is the centrifugal and coriolis term and is define as:

$$\begin{aligned} \mathbf{C}_{_{0}}(\mathbf{q},\dot{\mathbf{q}})=\left[ \begin{array}{cccc}0 &{} 0 &{} c_{_{13}} &{} 0\\ 0 &{} 0 &{} 0 &{} c_{_{24}}\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\end{array}\right] \end{aligned}$$

(44)

for which $c_{_{13}}=-LM_{c_{_{1}}}r_{_{w}}\cos (\alpha )\sin (\alpha +\delta _{c_{_{1}}}+\psi _{c_{_{1}}})\dot{\psi }_{c_{_{1}}}$ ,$c_{_{24}}=-LM_{c_{_{2}}}r_{_{w}}\cos (\alpha )\sin (\alpha +\delta _{c_{_{2}}}+\psi _{c_{_{2}}})\dot{\psi }_{c_{_{2}}}$, and $\mathbf{G}_{_{0}}(\mathbf{q})$ is the gravitational term defined as:

$$\begin{aligned} \mathbf{G}_{_{0}}(\mathbf{q})=g\left[ \begin{array}{c}g_{_{1}}\\ g_{_{2}}\\ g_{_{3}}\\ g_{_{4}}\end{array}\right] \end{aligned}$$

(45)

for which $g_{_{1}}$=$g(M_{c_{_{1}}}+2M_{w_{_{1}}})r_{_{w}}\sin (\alpha )$, $g_{_{2}}$=$g(M_{c_{_{2}}}+2M_{w_{_{2}}})r_{_{w}}\sin (\alpha )$, $g_{_{3}}$=$-gLM_{c_{_{1}}}\cos (\alpha )\sin (\delta _{c_{_{1}}}+\psi _{c_{_{1}}})$, $g_{_{4}}$=$-gLM_{c_{_{2}}}\cos (\alpha )\sin (\delta _{c_{_{2}}}+\psi _{c_{_{2}}})$, $g=9.8m/s^2$ is the gravitational acceleration constant, and $\mathbf{K}'$ is the stiffness matrix term defined as:

$$\begin{aligned} \mathbf{K}'=kr^{2}_{_{w}}\left[ \begin{array}{cccc}k_{_{11}} &{} k_{_{12}} &{} 0 &{} 0\\ k_{_{21}} &{} k_{_{22}} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\end{array}\right] \end{aligned}$$

(46)

for which $k_{_{11}}=1$, $k_{_{12}}=-1$, $k_{_{21}}=-1$, $k_{_{22}}=1$, k is the spring constant, and $\mathbf{u}=[u_{_{1}}\ u_{_{2}}\ 0\ 0]^\top$ is the input vector, where $u_{_{1}}$ and $u_{_{2}}$ are the inputs applied to the first vehicle and second vehicle of train system, respectively, and $\Delta \mathbf{H}(\mathbf{q})$, $\Delta \mathbf{C}(\mathbf{q},\dot{\mathbf{q}})$, and $\Delta \mathbf{G}(\mathbf{q})$ are the perturbed parametric matrices defined as follows:

$$\begin{aligned} \Delta \mathbf{H}(\mathbf{q})=\left[ \begin{array}{cccc}h'_{_{11}} &{} 0 &{} h'_{_{13}} &{} 0\\ 0 &{} h'_{_{22}} &{} 0 &{} h'_{_{24}}\\ h'_{_{31}} &{} 0 &{} h'_{_{33}} &{} 0\\ 0 &{} h'_{_{42}} &{} 0 &{} h'_{_{44}}\end{array}\right] \end{aligned}$$

(47)

where $h'_{_{11}}=2J_{w_{_{1}}}+\Delta M_{c_{_{1}}}r^{2}_{_{w}}+2\Delta M_{w_{_{1}}}r^{2}_{_{w}}+2J_{m_{_{1}}}\eta ^2$, $h'_{_{13}}=-2J_{m_{_{1}}}\eta ^2+L\Delta M_{c_{_{1}}}r_{_{w}}\cos (\alpha +\delta _{c_{_{1}}}+\psi _{c_{_{1}}})\cos (\alpha )$, $h'_{_{22}}=2J_{w_{_{2}}}+\Delta M_{c_{_{2}}}r^{2}_{_{w}}+2\Delta M_{w_{_{2}}}r^{2}_{_{w}}+2J_{m_{_{2}}}\eta ^2$, $h'_{_{24}}=-2J_{m_{_{2}}}\eta ^2+L\Delta M_{c_{_{2}}}r_{_{w}}\cos (\alpha +\delta _{c_{_{2}}}+\psi _{c_{_{2}}})\cos (\alpha )$, $h'_{_{31}}=-2J_{m_{_{1}}}\eta ^2+L\Delta M_{c_{_{1}}}r_{_{w}}\cos (\alpha +\delta _{c_{_{1}}}+\psi _{c_{_{1}}})\cos (\alpha )$, $h'_{_{33}}=J_{c_{_{1}}}+2J_{m_{_{1}}}\eta ^{2}+L^2\Delta M_{c_{_{1}}}\cos ^{2}(\alpha )$, $h'_{_{44}}=J_{c_{_{2}}}+2J_{m_{_{2}}}\eta ^{2}+L^2\Delta M_{c_{_{2}}}\cos ^{2}(\alpha )$.

$$\begin{aligned} \Delta \mathbf{C}(\mathbf{q},\dot{\mathbf{q}})=\left[ \begin{array}{cccc}0 &{} 0 &{} c'_{_{13}} &{} 0\\ 0 &{} 0 &{} 0 &{} c'_{_{24}}\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\end{array}\right] \end{aligned}$$

(48)

where $c'_{_{13}}=-L\Delta M_{c_{_{1}}}r_{_{w}}\cos (\alpha )\sin (\alpha +\delta _{c_{_{1}}}+\psi _{c_{_{1}}})\dot{\psi }_{c_{_{1}}}$ ,$c'_{_{24}}=-L\Delta M_{c_{_{2}}}r_{_{w}}\cos (\alpha )\sin (\alpha +\delta _{c_{_{2}}}+\psi _{c_{_{2}}})\dot{\psi }_{c_{_{2}}}$.

$$\begin{aligned} \Delta \mathbf{G}(\mathbf{q})=g\left[ \begin{array}{c}g'_{_{1}}\\ g'_{_{2}}\\ g'_{_{3}}\\ g'_{_{4}}\end{array}\right] \end{aligned}$$

(49)

for which $g'_{_{1}}$=$g(\Delta M_{c_{_{1}}}+2\Delta M_{w_{_{1}}})r_{_{w}}\sin (\alpha )$, $g'_{_{2}}$=$g(\Delta M_{c_{_{2}}}+2\Delta M_{w_{_{2}}})r_{_{w}}\sin (\alpha )$, $g'_{_{3}}$=$-gL\Delta M_{c_{_{1}}}\cos (\alpha ) \sin (\delta _{c_{_{1}}}+\psi _{c_{_{1}}})$, $g'_{_{4}}$=$-gL\Delta M_{c_{_{2}}}\cos (\alpha )\sin (\delta _{c_{_{2}}}+\psi _{c_{_{2}}})$, respectively.

From (42) and letting ${\varvec{x}}_{_{1}}=\mathbf{q}$, and ${\varvec{x}}_{_{2}}=\dot{\mathbf{q}}$ one gets:

$$\begin{aligned} \dot{\varvec{x}}= & {} \left[ \begin{array}{cc}\mathbf{0}_{(4)} &{} \mathbf{I}_{(4)} \\ -\mathbf{K}(\mathbf{q}) &{} -\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})\end{array}\right] \left[ \begin{array}{cc}{\varvec{x}}_{_{1}}\\ {\varvec{x}}_{_{2}}\end{array}\right] \nonumber \\&+\,\left[ \begin{array}{cc}\mathbf{0}_{(4\times 1)} \\ \Delta \mathbf{f}\end{array}\right] +\left[ \begin{array}{cc}\mathbf{0}_{(4\times 1)} \\ -\mathbf{G}(\mathbf{q})\end{array}\right] +\left[ \begin{array}{cc}\mathbf{0}_{(4)} \\ \mathbf{B}(\mathbf{q})\end{array}\right] \mathbf{u}\nonumber \\&+\,\left[ \begin{array}{cc}\mathbf{0}_{(4\times 1)} \\ \mathbf{d}\end{array}\right] \end{aligned}$$

(50)

where ${\varvec{x}}_{_{1}}=[x_{_{1}}\ x_{_{3}}\ x_{_{5}}\ x_{_{7}}]^\top =[\theta _{w_{_{1}}}\ \theta _{w_{_{2}}}\ \psi _{c_{_{1}}}\ \psi _{c_{_{2}}}]^\top$ is the rotation angle vector and ${\varvec{x}}_{_{2}}=[x_{_{2}}\ x_{_{4}}\ x_{_{6}}\ x_{_{8}}]^\top =[\dot{\theta }_{w_{_{1}}}\ \dot{\theta }_{w_{_{2}}}\ \dot{\psi }_{c_{_{1}}}\ \dot{\psi }_{c_{_{2}}}]^\top$ is the angular velocity vector.

Appendix B Proof of Lemma 2

Substituting (28), (30), and (31) into (25) one gets:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\mathbf{e}}_{_{1}}=\mathbf{e}_{_{2}}\\ \dot{\mathbf{e}}_{_{2}}=-\mathbf{e}_{_{1}}-3\mathbf{e}_{_{2}}-\mathbf{e}^{p(t)}_{_{1}}-\hbar {\varvec{\Phi }}^\top (\mathbf{s})\hat{\varvec{\Lambda }}{\varvec{\vartheta }}+\hbar {\varvec{\Phi }}^\top (\mathbf{s}){\varvec{\Lambda }}{\varvec{\vartheta }}\\ \qquad +{\varvec{\varepsilon }}-\Gamma _{\gamma _{_{1}}}sgn({\varvec{\chi }}_{_{1}})-\Gamma _{\gamma _{_{2}}}sgn({\varvec{\chi }}_{_{2}})+\mathbf{d}\\ \quad =-\mathbf{e}_{_{1}}-3\mathbf{e}_{_{2}}-\mathbf{e}^{p(t)}_{_{1}}{-}\hbar {\varvec{\Phi }}^\top (\mathbf{s})\tilde{\varvec{\Lambda }}{\varvec{\vartheta }}+{\varvec{\varepsilon }}\\ \qquad -\,\Gamma _{\gamma _{_{1}}}sgn({\varvec{\chi }}_{_{1}})-\Gamma _{\gamma _{_{2}}}sgn({\varvec{\chi }}_{_{2}})+\mathbf{d}\end{array}\right. \end{aligned}$$

(51)

where $\tilde{{\varvec{\Lambda }}}=\hat{\varvec{\Lambda }}-{\varvec{\Lambda }}$. From (51), the following is obtained:

$$\begin{aligned} \dot{\bar{\mathbf{e}}}= & {} {\varvec{\Upsilon }}\bar{\mathbf{e}}+\bar{\mathbf{B}}\big (-\mathbf{e}^{p(t)}_{_{1}}-\hbar {\varvec{\Phi }}^\top (\mathbf{s})\tilde{\varvec{\Lambda }}{\varvec{\vartheta }}+{\varvec{\varepsilon }}-\Gamma _{\gamma _{_{1}}}sgn({\varvec{\chi }}_{_{1}})\nonumber \\&-\Gamma _{\gamma _{_{2}}}sgn({\varvec{\chi }}_{_{2}})+\mathbf{d}\big ) \end{aligned}$$

(52)

where $\bar{\mathbf{e}}=[\mathbf{e}^\top _{_{1}}\ \mathbf{e}^\top _{_{2}}]^\top$, ${\varvec{\Upsilon }}=\left[ \begin{array}{cc}\mathbf{0}_{(2n)} &{} \mathbf{I}_{(2n)} \\ -\mathbf{I}_{(2n)} &{} -3\mathbf{I}_{(2n)}\end{array}\right] _{(4n)\times (4n)}$, and $\bar{\mathbf{B}}=\left[ \begin{array}{c}\mathbf{0}_{(2n)} \\ \mathbf{I}_{(2n)}\end{array}\right] _{(4n)\times 2n}$.

In order to achieve the approaching conditions of the sliding mode and guarantee the boundedness of the approximation error of the uncertainties, the Lyapunov function is selected as follows:

$$\begin{aligned} V(t)=\mathbf{s}^\top \mathbf{s}+\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{e}}+\frac{1}{2}tr(\tilde{\varvec{\Lambda }}^\top \tilde{\varvec{\Lambda }}) \end{aligned}$$

(53)

From (24), (28), (30), (31), and (52), the time derivative of (53) is

$$\begin{aligned} \dot{V}(t)= & {} \dot{\mathbf{s}}^\top \mathbf{s}+\mathbf{s}^\top \dot{\mathbf{s}}+\dot{\bar{\mathbf{e}}}^\top \mathbf{P}\bar{\mathbf{e}}+\bar{\mathbf{e}}^\top \mathbf{P}\dot{\bar{\mathbf{e}}}+tr\big (\tilde{\varvec{\Lambda }}^\top \dot{\hat{{\varvec{\Lambda }}}}\big )\nonumber \\= & {} \bar{\mathbf{e}}^\top ({\varvec{\Upsilon }}^\top \mathbf{P}+\mathbf{P}{\varvec{\Upsilon }})\bar{\mathbf{e}}-(\mathbf{e}^{p(t)}_{_{1}})^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{e}_{_{1}}^{p(t)}\nonumber \\&+\,\big ({\varvec{\varepsilon }}+\mathbf{d}-\Gamma _{\gamma _{_{1}}}sgn({\varvec{\chi }}_{_{1}})-\Gamma _{\gamma _{_{2}}}sgn({\varvec{\chi }}_{_{2}})\big )^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&+\,\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\big ({\varvec{\varepsilon }}+\mathbf{d}-\Gamma _{\gamma _{_{1}}}sgn({\varvec{\chi }}_{_{1}})-\Gamma _{\gamma _{_{2}}}sgn({\varvec{\chi }}_{_{2}})\big )+\big ({\varvec{\varepsilon }}\nonumber \\&+\,\mathbf{d}-\Gamma _{\gamma _{_{2}}}sgn({\varvec{\chi }}_{_{2}})-\Gamma _{\gamma _{_{1}}}sgn({\varvec{\chi }}_{_{1}})\big )^\top \mathbf{s}\nonumber \\&+\,\mathbf{s}^\top \big ({\varvec{\varepsilon }}+\mathbf{d}-\Gamma _{\gamma _{_{2}}}sgn({\varvec{\chi }}_{_{2}})-\Gamma _{\gamma _{_{1}}}sgn({\varvec{\chi }}_{_{1}})\big )\nonumber \\&+\,tr\Big ({\tilde{{\varvec{\Lambda }}}}^\top \big ({{\dot{\hat{{\varvec{\Lambda }}}}}}-2\hbar {\varvec{\Phi }}(\mathbf{s})(\mathbf{s}+\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}){\varvec{\vartheta }}^\top \big )\Big ) \end{aligned}$$

(54)

From (32) and (38) one gets

$$\begin{aligned} \dot{V}(t)= & {} -\bar{\mathbf{e}}^\top _{_{i}}\mathbf{Q}_i\bar{\mathbf{e}}_{_{i}}+\big ({\varvec{\gamma }}_{_{1}}-\Gamma _{\gamma _{_{1}}}sgn({\varvec{\chi }}_{_{1}})\big )^\top \mathbf{s}\nonumber \\&+\,\mathbf{s}^\top \big ({\varvec{\gamma }}_{_{1}}-\Gamma _{\gamma _{_{1}}}sgn({\varvec{\chi }}_{_{1}})\big )\nonumber \\&+\,\big ({\varvec{\gamma }}_{_{2}}-\Gamma _{\gamma _{_{2}}}sgn({\varvec{\chi }}_{_{2}})\big )^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&+\,\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\big ({\varvec{\gamma }}_{_{2}}-\Gamma _{\gamma _{_{2}}}sgn({\varvec{\chi }}_{_{2}})\big )\nonumber \\&-\,(\mathbf{e}^{p(t)}_{_{1}})^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{e}_{_{1}}^{p(t)} \end{aligned}$$

(55)

From Assumption 3,

$$\begin{aligned} \dot{V}(t)\le & {} -\bar{\mathbf{e}}^\top \mathbf{Q}\bar{\mathbf{e}}-2\zeta _{_{1}}\Vert \mathbf{s}\Vert -2\zeta _{_{2}}\Vert \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\Vert \nonumber \\&-\,(\mathbf{e}^{p(t)}_{_{1}})^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{e}^{p(t)}_{_{1}}+\big ({\varvec{\gamma }}_{_{1}}-\zeta _{\gamma _{_{1}}}sgn({\varvec{\chi }}_{_{1}})\big )^\top \mathbf{s}\nonumber \\&+\,\mathbf{s}^\top \big ({\varvec{\gamma }}_{_{1}}-\zeta _{\gamma _{_{1}}}sgn({\varvec{\chi }}_{_{1}})\big )\nonumber \\&+\,\big ({\varvec{\gamma }}_{_{2}}-\zeta _{\gamma _{_{2}}}sgn({\varvec{\chi }}_{_{2}})\big )^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&+\,\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\big ({\varvec{\gamma }}_{_{2}}-\zeta _{\gamma _{_{2}}}sgn({\varvec{\chi }}_{_{2}})\big ) \end{aligned}$$

(56)

Since

$$\begin{aligned} \mathbf{s}^\top \big ({\varvec{\gamma }}_{_{1}}-\zeta _{\gamma _{_{1}}}sgn({\varvec{\chi }}_{_{1}})\big )+\big ({\varvec{\gamma }}_{_{1}}-\zeta _{\gamma _{_{1}}}sgn({\varvec{\chi }}_{_{1}})\big )^\top \mathbf{s}\le 0 \end{aligned}$$

(57)

and

$$\begin{aligned}&\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\big ({\varvec{\gamma }}_{_{2}}-\zeta _{\gamma _{_{2}}}sgn({\varvec{\chi }}_{_{2}})\big )\nonumber \\&\quad +\big ({\varvec{\gamma }}_{_{2}}-\zeta _{\gamma _{_{2}}}sgn({\varvec{\chi }}_{_{2}})\big )^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\le 0 \end{aligned}$$

(58)

and letting $\lambda _{_{1}}<1$, the following is obtained

$$\begin{aligned} \dot{V}(t)\le & {} -\bar{\mathbf{e}}^\top \mathbf{Q}\bar{\mathbf{e}}-2\zeta _{_{1}}\Vert \mathbf{s}\Vert \nonumber \\&+\,\lambda _{_{1}}(\mathbf{e}^{p(t)}_{_{1}})^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}+\lambda _{_{1}}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{e}^{p(t)}_{_{1}}\nonumber \\&-\,(1+\lambda _{_{1}})(\mathbf{e}^{p(t)}_{_{1}})^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-(1+\lambda _{_{1}})\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{e}^{p(t)}_{_{1}}\nonumber \\ \end{aligned}$$

(59)

From Lemma 1, one gets:

$$\begin{aligned} \dot{V}(t)\le & {} -\bar{\mathbf{e}}^\top \mathbf{Q}\bar{\mathbf{e}}-2\zeta _{_{1}}\Vert \mathbf{s}\Vert +\frac{\lambda _{_{1}}}{\varsigma _{_{1}}}\left( \mathbf{e}^{p(t)}_{_{1}}\right) ^\top \left( \mathbf{e}^{p(t)}_{_{1}}\right) \nonumber \\&+\,\lambda _{_{1}}\varsigma _{_{1}}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-(1+\lambda _{_{1}})\left( \mathbf{e}^{p(t)}_{_{1}}\right) ^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&-\,(1+\lambda _{_{1}})\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{e}^{p(t)}_{_{1}}\nonumber \\= & {} -\,2\zeta _{_{1}}\Vert \mathbf{s}\Vert -[\bar{\mathbf{e}}^\top \ \left( \mathbf{e}^{p(t)}_{_{1}})^\top \right] \left[ \begin{array}{cc}\bar{\mathbf{Q}}_{_{1}} &{} \bar{\mathbf{Q}}_{_{2}}\\ \bar{\mathbf{Q}}^\top _{_{2}} &{}\bar{\mathbf{Q}}\end{array}\right] \left[ \begin{array}{cc}\bar{\mathbf{e}}\\ \mathbf{e}^{p(t)}_{_{1}}\end{array}\right] \nonumber \\= & {} -\,2\zeta _{_{1}}\Vert \mathbf{s}\Vert -\tilde{\mathbf{e}}^\top \bar{\mathbf{Q}}\tilde{\mathbf{e}}\le 0 \end{aligned}$$

(60)

where $\tilde{\mathbf{e}}^\top =[\bar{\mathbf{e}}^\top \ (\mathbf{e}^{p(t)}_{_{1}})^\top ]$ and $\bar{\mathbf{Q}}=\left[ \begin{array}{cc}\bar{\mathbf{Q}}_{_{1}} &{} \bar{\mathbf{Q}}_{_{2}}\\ \bar{\mathbf{Q}}^\top _{_{2}} &{} \bar{\mathbf{Q}}_{_{3}}\end{array}\right] >0$ for which $\bar{\mathbf{Q}}_{_{1}}=\mathbf{Q}-\lambda _{_{1}}\varsigma _{_{1}}\mathbf{P}\bar{\mathbf{B}}\bar{\mathbf{B}}^\top \mathbf{P}$, $\bar{\mathbf{Q}}_{_{2}}=(1+\lambda _{_{1}})\mathbf{P}\bar{\mathbf{B}}$, and $\bar{\mathbf{Q}}_{_{3}}=-\frac{\lambda _{_{1}}}{\varsigma _{_{1}}}\mathbf{I}_{(2n)}$. Using Barbalat’s lemma in [40], (60) implies $\mathbf{s}\rightarrow 0$ and $\bar{\mathbf{e}}\rightarrow 0$ ($\mathbf{e}\rightarrow 0$) as $t\rightarrow \infty$. This completes the proof. $\square$

Appendix C Proof of Theorem 2

Similar to the proof of Lemma 2, where the same Lyapunov function is chosen as in (53). Condition 1:$|\chi _{_{{l}_{\varphi }}}|>\epsilon$. From (22), (28), (30), (35), (36), (37), then,

$$\begin{aligned} \dot{V}(t)= & {} \big ({\varvec{\gamma }}_{_{3}}-\Gamma _{\gamma _{_{3}}}sgn({\varvec{\chi }}_{_{1}})\big )^\top \mathbf{s}+\mathbf{s}^\top \big ({\varvec{\gamma }}_{_{3}}-\Gamma _{\gamma _{_{3}}}sgn({\varvec{\chi }}_{_{1}})\big )\nonumber \\&+\,\big ({\varvec{\gamma }}_{_{4}}-\Gamma _{\gamma _{_{4}}}sgn({\varvec{\chi }}_{_{2}})\big )^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&+\,\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\big ({\varvec{\gamma }}_{_{4}}-\Gamma _{\gamma _{_{4}}}sgn({\varvec{\chi }}_{_{2}})\big )\nonumber \\&+\,\bar{\mathbf{e}}^\top ({\varvec{\Upsilon }}^\top \mathbf{P}+\mathbf{P}{\varvec{\Upsilon }})\bar{\mathbf{e}}-\frac{2}{\rho ^2}\mathbf{s}^\top \mathbf{s}\nonumber \\&-\,\frac{2}{\rho ^2}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{s}-\varpi \mathbf{s}^\top \mathbf{s}+\mathbf{d}^\top \mathbf{s}\nonumber \\&+\,\mathbf{s}^\top \mathbf{d}-(\mathbf{e}^{p(t)}_{_{1}})^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{e}^{p(t)}_{_{1}}\nonumber \\&-\,\frac{2}{\rho ^2}\mathbf{s}^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-\frac{2}{\rho ^2}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-\varpi \mathbf{s}^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&+\,\mathbf{d}^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}+\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{d}\nonumber \\&+\,tr\Big ({\tilde{{\varvec{\Lambda }}}}^\top \big ({{\dot{\hat{{\varvec{\Lambda }}}}}}-2\hbar {\varvec{\Phi }}(\mathbf{s})(\mathbf{s}+\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}){\varvec{\vartheta }}^\top \big )\Big ) \end{aligned}$$

(61)

From (38), adaptive law (32), Lemma 1, let $\lambda _{_{2}}<1$, and Assumption 4 ($\mathbf{s}^\top \big ({\varvec{\gamma }}_{_{3}}-\zeta _{\gamma _{_{3}}}sgn({\varvec{\chi }}_{_{1}})\big )+\big ({\varvec{\gamma }}_{_{3}}-\zeta _{\gamma _{_{3}}}sgn({\varvec{\chi }}_{_{1}})\big )^\top \mathbf{s}\le 0$, $\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\big ({\varvec{\gamma }}_{_{4}}-\zeta _{\gamma _{_{4}}}sgn({\varvec{\chi }}_{_{2}})\big )+\big ({\varvec{\gamma }}_{_{4}}-\zeta _{\gamma _{_{4}}}sgn({\varvec{\chi }}_{_{2}})\big )^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\le 0$) one gets:

$$\begin{aligned} \dot{V}(t)\le & {} -\bar{\mathbf{e}}^\top \mathbf{Q}\bar{\mathbf{e}}-\frac{2}{\rho ^2}\mathbf{s}^\top \mathbf{s}-\frac{2}{\rho ^2}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{s}-\varpi \mathbf{s}^\top \mathbf{s}+\mathbf{d}^\top \mathbf{s}\nonumber \\&+\,\mathbf{s}^\top \mathbf{d}+\frac{\lambda _{_{2}}}{\varsigma _{_{2}}}\left( \mathbf{e}^{p(t)}_{_{1}}\right) ^\top \left( \mathbf{e}^{p(t)}_{_{1}}\right) \nonumber \\&+\,\lambda _{_{2}}\varsigma _{_{2}}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-\frac{2}{\rho ^2}\mathbf{s}^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&-\,(1+\lambda _{_{2}})\left( \mathbf{e}^{p(t)}_{_{1}}\right) ^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-(1+\lambda _{_{2}})\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{e}^{p(t)}_{_{1}}\nonumber \\&-\,\frac{2}{\rho ^2}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-\varpi \mathbf{s}^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}+\mathbf{d}\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}+\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{d}\nonumber \\= & {} -\,\bar{\mathbf{e}}^\top \mathbf{Q}\bar{\mathbf{e}}-\frac{2}{\rho ^2}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{s}-\varpi \mathbf{s}^\top \mathbf{s}\nonumber \\&+\,\frac{\lambda _{_{2}}}{\varsigma _{_{2}}}(\mathbf{e}^{p(t)}_{_{1}})^\top (\mathbf{e}^{p(t)}_{_{1}})+\lambda _{_{2}}\varsigma _{_{2}}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&-\,(1+\lambda _{_{2}})\left( \mathbf{e}^{p(t)}_{_{1}}\right) ^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&-\,(1+\lambda _{_{2}})\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{e}^{p(t)}_{_{1}}-\frac{2}{\rho ^2}\mathbf{s}^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-\varpi \mathbf{s}^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&+\,2\rho ^2\mathbf{d}^\top \mathbf{d}-\left( \frac{1}{\rho }\mathbf{s}-\rho \mathbf{d}\right) ^\top \left( \frac{1}{\rho }\mathbf{s}-\rho \mathbf{d}\right) \nonumber \\&-\,\left( \frac{1}{\rho }\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-\rho \mathbf{d}\right) ^\top \left( \frac{1}{\rho }\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-\rho \mathbf{d}\right) \nonumber \\\le & {} -\,\bar{\mathbf{e}}^\top \mathbf{Q}\bar{\mathbf{e}}-\frac{2}{\rho ^2}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{s}-\varpi \mathbf{s}^\top \mathbf{s}\nonumber \\&+\,\frac{\lambda _{_{2}}}{\varsigma _{_{2}}}\left( \mathbf{e}^{p(t)}_{_{1}}\right) ^\top (\mathbf{e}^{p(t)}_{_{1}})+\lambda _{_{2}}\varsigma _{_{2}}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&-\,(1+\lambda _{_{2}})\left( \mathbf{e}^{p(t)}_{_{1}}\right) ^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&-\,(1+\lambda _{_{2}})\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{e}^{p(t)}_{_{1}}-\frac{2}{\rho ^2}\mathbf{s}^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&-\,\varpi \mathbf{s}^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}+2\rho ^2\mathbf{d}^\top \mathbf{d}\nonumber \\= & {} -\,\bar{\mathbf{e}}^\top \mathbf{Q}\bar{\mathbf{e}}+\frac{\lambda _{_{2}}}{\varsigma _{_{2}}}\left( \mathbf{e}^{p(t)}_{_{1}}\right) ^\top \left( \mathbf{e}^{p(t)}_{_{1}}\right) +\lambda _{_{2}}\varsigma _{_{2}}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&-\,(1+\lambda _{_{2}})\left( \mathbf{e}^{p(t)}_{_{1}}\right) ^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-(1+\lambda _{_{2}})\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{e}^{p(t)}_{_{1}}\nonumber \\&+\,2\rho ^2\mathbf{d}^\top \mathbf{d}+800\bar{\mathbf{e}}^\top \bar{\mathbf{e}}-\bar{\mathbf{s}}^\top \bar{\mathbf{E}}\bar{\mathbf{s}}\end{aligned}$$

(62)

where $\bar{\mathbf{s}}^\top =[\mathbf{s}^\top \ \bar{\mathbf{e}}^\top ]^\top$, $\mathbf{E}=\frac{2}{\rho ^2}\bar{\mathbf{B}}^\top \mathbf{P}+\frac{1}{2}\varpi \bar{\mathbf{B}}^\top \mathbf{P}$, and $\bar{\mathbf{E}}=\left[ \begin{array}{cc}\varpi \mathbf{I}_{(2n)} &{} \mathbf{E}\\ \mathbf{E}^\top &{} 800\mathbf{I}_{(4n)}\end{array}\right] >0$. Since $\bar{\mathbf{s}}^\top \bar{\mathbf{s}}=\mathbf{s}^\top \mathbf{s}+\bar{\mathbf{e}}^\top \bar{\mathbf{e}}\ge \bar{\mathbf{e}}^\top \bar{\mathbf{e}}$, we have $-\lambda _{max}(\bar{\mathbf{E}})\bar{\mathbf{s}}^\top \bar{\mathbf{s}}\le -\lambda _{max}(\bar{\mathbf{E}})\bar{\mathbf{e}}^\top \bar{\mathbf{e}}$ for which $\lambda _{max}(\bar{\mathbf{E}})$ denotes the maximum eigenvalue of $\bar{\mathbf{E}}$. Hence, (62) can be rewritten as

$$\begin{aligned} \dot{V}(t)\le & {} -\bar{\mathbf{e}}^\top \mathbf{Q}\bar{\mathbf{e}}+\frac{\lambda _{_{2}}}{\varsigma _{_{2}}}(\mathbf{e}^{p(t)}_{_{1}})^\top (\mathbf{e}^{p(t)}_{_{1}})+\lambda _{_{2}}\varsigma _{_{2}}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&-\,(1+\lambda _{_{2}})(\mathbf{e}^{p(t)}_{_{1}})^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-(1+\lambda _{_{2}})\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{e}^{p(t)}_{_{1}}\nonumber \\&+\,2\rho ^2\mathbf{d}^\top \mathbf{d}+800\bar{\mathbf{e}}^\top \bar{\mathbf{e}}-\lambda _{max}(\bar{\mathbf{E}})\bar{\mathbf{e}}^\top \bar{\mathbf{e}}\nonumber \\= & {} -\,[\bar{\mathbf{e}}^\top \ (\mathbf{e}^{p(t)}_{_{1}})^\top ]\left[ \begin{array}{cc}\bar{\mathbf{N}}_{_{1}} &{} \bar{\mathbf{N}}_{_{2}}\\ \bar{\mathbf{N}}^\top _{_{2}} &{} \bar{\mathbf{N}}_{_{3}}\end{array}\right] \left[ \begin{array}{cc}\bar{\mathbf{e}}\\ \mathbf{e}^{p(t)}_{_{1}}\end{array}\right] \nonumber \\&+\,2\rho _{_{i}}^2\mathbf{d}^\top _i\mathbf{d}_{_{i}}\nonumber \\= & {} -\,\tilde{\mathbf{e}}^\top \bar{\mathbf{N}}\tilde{\mathbf{e}}+2\rho ^2\mathbf{d}^\top \mathbf{d}\end{aligned}$$

(63)

where $\bar{\mathbf{N}}=\left[ \begin{array}{cc}\bar{\mathbf{N}}_{_{1}} &{} \bar{\mathbf{N}}_{_{2}}\\ \bar{\mathbf{N}}^\top _{_{2}} &{} \bar{\mathbf{N}}_{_{3}}\end{array}\right] >0$ for which $\bar{\mathbf{N}}_{_{1}}=\mathbf{Q}+\lambda _{max}(\bar{\mathbf{E}})\mathbf{I}_{(4n)}-800\mathbf{I}_{(4n)}-\lambda _{_{2}}\varsigma _{_{2}}\mathbf{P}\bar{\mathbf{B}}\bar{\mathbf{B}}^\top \mathbf{P}$, $\bar{\mathbf{N}}_{_{2}}=(1+\lambda _{_{2}})\mathbf{P}\bar{\mathbf{B}}$, and $\bar{\mathbf{N}}_{_{3}}=-\frac{\lambda _{_{2}}}{\varsigma _{_{2}}}\mathbf{I}_{(2n)}$. Since $\mathbf{H}_{_{0}}(\mathbf{q})$ is nonsingular, $\forall \mathbf{q}$, and then $\mathbf{H}_{_{0}}(\mathbf{q})^{-1}$ is bounded, thus, $\mathbf{d}=\mathbf{M}_{_{0}}(\mathbf{q})^{-1}\mathbf{d}'$ is also bounded and so is $\Vert \mathbf{d}\Vert$. Therefore, from (63), the following is obtained:

$$\begin{aligned} \dot{V}(t)\le & {} -\bar{\mathbf{N}}\Vert \tilde{\mathbf{e}}\Vert ^2+2\rho ^2\Vert \mathbf{d}\Vert ^2\nonumber \\\le & {} -\lambda _{min}(\bar{\mathbf{N}})\Vert \tilde{\mathbf{e}}\Vert ^2+2\rho ^2\Vert {\mathbf{d}}\Vert ^2 \end{aligned}$$

(64)

where $\lambda _{min}(\bar{\mathbf{N}})$ denotes the minimal eigenvalue of $\bar{\mathbf{N}}$. Therefore, whenever

$$\begin{aligned} \Vert \tilde{\mathbf{e}}\Vert \ge \frac{\rho \sqrt{2\Vert \mathbf{d}\Vert ^2}}{\sqrt{\lambda _{min}(\bar{\mathbf{N}})}}\ , \end{aligned}$$

(65)

$\dot{V}(t)\le 0$. In light of the Lyapunov stability theory of the retarded functional differential equation, since $\rho$ is the design constant serving as an attenuation level, it can be concluded from (63) that for any $t\ge t_0$, $\bar{\mathbf{e}}$ and $\tilde{\varvec{\Lambda }}$ are UUB in the presence of the external disturbance $\mathbf{d}(t)$. Assuming $\mathbf{d}(t) \in L_2[0,T]$, $\forall T \in [0,\infty )$ and since $V(T)\ge 0$, integrating (63) from $t=0$ to $t=T$ leads to:

$$\begin{aligned} \int ^T_0\tilde{\mathbf{e}}^\top \bar{\mathbf{N}}\tilde{\mathbf{e}}dt \le V(0)+2\rho ^2\int ^T_0 \mathbf{d}^\top \mathbf{d}dt \end{aligned}$$

(66)

Substituting (53) into (66), for the $H_\infty$ tracking performance J is given by:

$$\begin{aligned} J= & {} \int ^T_0\tilde{\mathbf{e}}^\top \bar{\mathbf{N}}\tilde{\mathbf{e}}dt\le \mathbf{s}^\top (0)\mathbf{s}(0)+\bar{\mathbf{e}}^\top (0)\mathbf{P}\bar{\mathbf{e}}(0)\nonumber \\&+\frac{1}{2}tr(\tilde{\varvec{\Lambda }}^\top (0)\tilde{\varvec{\Lambda }}(0))+2\rho ^2\int ^T_0\mathbf{d}^\top \mathbf{d}dt \end{aligned}$$

(67)

Condition 2: If $|\chi _{_{{l}_{\varphi }}}|\le \epsilon$. From (61),

$$\begin{aligned} \dot{V}(t)= & {} \big ({\varvec{\gamma }}_{_{5}}-(\Gamma _{\gamma _{_{3}}}/\epsilon ){\varvec{\chi }}_{_{1}}\big )^\top \mathbf{s}+\mathbf{s}^\top \big ({\varvec{\gamma }}_{_{5}}-(\Gamma _{\gamma _{_{3}}}/\epsilon ){\varvec{\chi }}_{_{1}}\big )\nonumber \\&+\,\big ({\varvec{\gamma }}_{_{6}}-(\Gamma _{\gamma _{_{4}}}/\epsilon ){\varvec{\chi }}_{_{2}}\big )^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&+\,\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\big ({\varvec{\gamma }}_{_{6}}-(\Gamma _{\gamma _{_{4}}}/\epsilon ){\varvec{\chi }}_{_{2}}\big )\nonumber \\&+\,\bar{\mathbf{e}}^\top ({\varvec{\Upsilon }}^\top \mathbf{P}+\mathbf{P}{\varvec{\Upsilon }})\bar{\mathbf{e}}-\frac{2}{\rho ^2}\mathbf{s}^\top \mathbf{s}-\frac{2}{\rho ^2}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{s}\nonumber \\&-\,\varpi \mathbf{s}^\top \mathbf{s}+\mathbf{d}^\top \mathbf{s}+\mathbf{s}^\top \mathbf{d}\nonumber \\&-\,(\mathbf{e}^{p(t)}_{_{1}})^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{e}^{p(t)}_{_{1}}\nonumber \\&-\,\frac{2}{\rho ^2}\mathbf{s}^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}-\frac{2}{\rho ^2}\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\nonumber \\&-\,\varpi \mathbf{s}^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}+\mathbf{d}^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}+\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\mathbf{d}\nonumber \\&+\,tr\Big ({\tilde{{\varvec{\Lambda }}}}^\top \big ({{\dot{\hat{{\varvec{\Lambda }}}}}}-2\hbar {\varvec{\Phi }}(\mathbf{s})(\mathbf{s}+\bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}){\varvec{\vartheta }}^\top \big )\Big ) \end{aligned}$$

(68)

It follows from the above proof and from (38), adaptive law (32), Lemma 1, for $\lambda _{_{2}}<1$, and Assumption 5 ($\mathbf{s}^\top \big ({\varvec{\gamma }}_{_{5}}-(\zeta _{\gamma _{_{3}}}/\epsilon ){\varvec{\chi }}_{_{1}}\big )+\big ({\varvec{\gamma }}_{_{5}}-(\zeta _{\gamma _{_{3}}}/\epsilon ){\varvec{\chi }}_{_{1}}\big )^\top \mathbf{s}\le 0$ and $\bar{\mathbf{e}}^\top \mathbf{P}\bar{\mathbf{B}}\big ({\varvec{\gamma }}_{_{6}}-(\zeta _{\gamma _{_{4}}}/\epsilon ){\varvec{\chi }}_{_{2}}\big )+\big ({\varvec{\gamma }}_{_{6}}-(\zeta _{\gamma _{_{4}}}/\epsilon ){\varvec{\chi }}_{_{2}}\big )^\top \bar{\mathbf{B}}^\top \mathbf{P}\bar{\mathbf{e}}\le 0$) the same results can be obtained. Hence, the $H_\infty$ tracking performance satisfies

$$\begin{aligned} J= & {} \int ^T_0\tilde{\mathbf{e}}^\top \bar{\mathbf{N}}\tilde{\mathbf{e}}dt\le \mathbf{s}^\top (0)\mathbf{s}(0)+\bar{\mathbf{e}}^\top (0)\mathbf{P}\bar{\mathbf{e}}(0)\nonumber \\&+\,\frac{1}{2}tr(\tilde{\varvec{\Lambda }}^\top (0)\tilde{\varvec{\Lambda }}(0))+2\rho ^2\int ^T_0\mathbf{d}^\top \mathbf{d}dt \end{aligned}$$

(69)

This completes the proof. $\square$