Skip to main content
Springer Nature Link
Log in

Vibration analysis of dynamically loaded bearing with distributed defect based on defect induced excitation

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

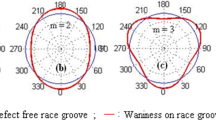
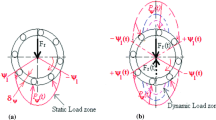
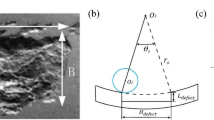
In the present study an investigation has been carried out to determine distributed defect induced excitations in a bearing subjected to an external load which is a combination of static and dynamic load. The dynamic component of external load has been considered to be harmonic in nature and may be due to the shaft unbalance. The race surface waviness in radial direction has been taken in to account as the distributed defects in bearings. The race waviness is modeled mathematically, as sinusoidal functions of different orders and superposition of sinusoidal functions as well. Equal and random amplitudes of different orders have been considered. Kinematic and dynamic parameters as well as contact forces resulted due to race-rolling element interaction as obtained from published literature have been modified and extended to consider radial waviness and external dynamic loading. The frequency spectra of nonlinear contact forces causing excitations have been obtained. For static radial loading, these spectra are in accordance with those obtained for responses of linear dynamic models. For external dynamic loading, however, additional spectral components as sidebands at shaft frequency about the significant frequencies corresponding to external static loading have been observed for both inner and outer race surface waviness, when modeled as sinusoidal function of any order. Additional spectral components have also been observed for outer race waviness when formulated as superposition of different orders whereas for inner race, there are some amplitude variations in spectral components compared to that of static loading. Variation in amplitudes of spectral components has also been resulted when random values were assigned to different orders of waviness.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Abbreviations

a :

A whole number

A :

Amplitude

b :

A whole number

d :

Diameter of rolling element

D :

Pitch diameter of bearing

e :

Excitation at each race roller contact in radial direction

E :

Total excitation in vertical direction

\(f_{id}\) :

Ball passing frequency inner race

\(f_{od}\) :

Ball passing frequency outer race

\(f_{s}\) :

Shaft frequency

\(F_{r}\) :

Radial loading

\(J_{\mathrm{r}}\) :

Radial integral

K :

Load-deformation constant

L :

Effective length of roller

m :

Order of waviness

n :

\(\hbox {n}\mathrm{th}\) revolution

p :

An integer

P :

Contact force in a defect free bearing

\(p_{d}\) :

Diametral clearance of bearing

\(P_{w}\) :

Net contact force after considering contact waviness

q :

An integer

r :

Groove radius

R :

Referred rolling element when load acting downwards

S :

Rolling element immediate from direction of load when load acting upwards

u :

Magnitude of race waviness

t :

Instantaneous time

w :

Waviness in contact with roller

W :

Static load

X :

Number of rolling elements from reference roller, \(\hbox {R}_{1}\) to meet \(\hbox {S}_{1}\)

WO :

Any arbitrary value of waviness

Z :

No. of rolling elements

\(\alpha \) :

Nominal contact angle

\(\omega \) :

Circular frequency

\(\beta \) :

Phase difference

\(\delta \) :

Elastic deformation at race roller contact

\(\vartheta \) :

Load-deformation index

\(\upkappa \) :

A constant

\(\varepsilon \) :

Load distribution factor

\(\pm \psi _{l}\) :

Extent of load zone

c :

Cage

h :

Harmonic load

i :

Inner race

l :

Line of action of external load

max :

Maximum

o :

Outer race

s:

Shaft

w :

After considering waviness

References

  1. Sunnersjo CS (1978) Varying compliance vibrations of rolling bearings. J Sound Vib 58(3):363–373. doi:10.1016/S0022-460X(78)80044-3

    Article  Google Scholar 

  2. Akturk N, Uneeb M, Gohar R (1997) The effects of number of balls and preload on vibrations associated with ball bearings. J Tribol 119(4):747–753. doi:10.1115/1.2833880

    Article  Google Scholar 

  3. White MF (1979) Rolling element bearing vibration transfer characteristics: effect of stiffness. J Appl Mech 46(3):677–684. doi:10.1115/1.3424626

    Article  MATH  Google Scholar 

  4. Yhland EM (1992) A linear theory of vibration caused by ball bearings with form errors operating at moderate speeds. J Tribol 114(2):348–359. doi:10.1115/1.2920894

    Article  Google Scholar 

  5. Yhland EM (1967) Waviness measurement-an instrument for quality control in rolling bearing industry. Proc Inst Mech Eng 182(11):438–445. doi:10.1243/PIME_CONF_1967_182_341_02

    Google Scholar 

  6. Tandon N, Choudhury A (1999) A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings. Tribol Int 32(8):469–480. doi:10.1016/S0301-679X(99)00077-8

    Article  Google Scholar 

  7. Meyer LD, Weichbrodt B, Ahlgren FF (1980) An analytical model for ball bearing vibrations to predict vibration response to distributed defects. J Mech Des 102(2):205–210. doi:10.1115/1.3254731

    Article  Google Scholar 

  8. Choudhury A, Tandon N (1998) A theoretical model to predict vibration response of rolling bearings to distributed defects under radial load. J Vib Acoust 120(1):214–220. doi:10.1115/1.2893808

    Article  Google Scholar 

  9. Wardle FP (1988) Vibration forces produced by waviness of the rolling surfaces of thrust loaded ball bearings Part 1: theory. J Mech Eng Sci 202(5):305–312 10.1243/PIME_PROC_ 1988_202_127_02

    Article  Google Scholar 

  10. Wardle FP (1988) Vibration forces produced by waviness of the rolling surfaces of thrust loaded ball bearings Part 2: experimental validation. J Mech Eng Sci 202(5):313–319. doi:10.1243/PIME_PROC_1988_202_128_02

    Article  Google Scholar 

  11. Aktürk N (1999) The effect of waviness on vibrations associated with ball bearings. J Tribol 121(4):667–677. doi:10.1115/1.2834121

    Article  Google Scholar 

  12. Ono K, Okada Y (1998) Analysis of ball bearing vibrations caused by outer race waviness. J Vib Acoust 120(4):901–908. doi:10.1115/1.2893918

    Article  Google Scholar 

  13. El-Thalji I, Jantunen E (2015) Fault analysis of the wear fault development in rolling bearings. Eng Fail Anal 57:470–482. doi:10.1016/j.engfailanal.2015.08.013

    Article  Google Scholar 

  14. Jang GH, Jeong SW (2002) Nonlinear excitation model of ball bearings in a rigid rotor supported by two or more ball bearings considering five degrees of freedom. J Tribol 124(1):82–90. doi:10.1115/1.1398289

    Article  Google Scholar 

  15. Jang GH, Jeong SW (2004) Vibration analysis of a rotating system due to the effect of ball bearing waviness. J Sound Vib 269(3–5):709–726. doi:10.1016/S0022-460X(03)00127-5

    Article  Google Scholar 

  16. Changqing B (2005) Dynamic model of ball bearings with internal clearance and waviness. J Sound Vib 294(1–2):23–48. doi:10.1016/j.jsv.2005.10.005

    Google Scholar 

  17. Sopanen J, Mikkola A (2003) Dynamic model of a deep-groove ball bearing including localized and distributed defects Part 1: theory. J Multi Body Dyn 217(3):201–211. doi:10.1243/14644190360713551

    Google Scholar 

  18. Tandon N, Choudhury A (2000) A theoretical model to predict the vibration response of rolling bearings in a rotor bearing system to distributed defects under radial load. J Tribol 122(3):609–615. doi:10.1115/1.555409

    Article  Google Scholar 

  19. Babu CK, Tandon N, Pandey RK (2012) Vibration modeling of a rigid rotor supported on the lubricated angular contact ball bearings considering six degrees of freedom and waviness on balls and races. J Vib Acoust 134(1):1–12. doi:10.1115/1.4005140

    Article  Google Scholar 

  20. Harsha SP, Sandeep K, Prakash R (2004) Nonlinear dynamic behaviors of rolling element bearings due to surface waviness. J Sound Vib 272(3–5):557–580. doi:10.1016/S0022-460X(03)00384-5

    Article  Google Scholar 

  21. Harsha SP (2006) Nonlinear dynamic analysis of a high-speed rotor supported by rolling element bearings. J Sound Vib 290(1–2):65–100. doi:10.1016/j.jsv.2005.03.008

    Article  Google Scholar 

  22. Harsha SP (2005) Nonlinear dynamic response of a balanced rotor supported on rolling element bearings. Mech Syst Signal Process 19(3):551–578. doi:10.1016/j.ymssp.2004.04.002

    Article  Google Scholar 

  23. Harsha SP, Kankar PK (2004) Stability analysis of a rotor bearing system due to surface waviness and number of balls. Int J Mech Sci 46(7):1057–1081. doi:10.1016/j.ijmecsci.2004.07.007

    Article  MATH  Google Scholar 

  24. Kankar PK, Satish C, Sharma Harsha SP (2012) Nonlinear vibration signature analysis of a high speed rotor bearing system due to race imperfection. J Comput Nonlinear Dyn 7(1):011014–011016. doi:10.1115/1.4004962

    Article  Google Scholar 

  25. Su YT, Lin MH, Lee MS (1993) The effects of surface irregularities on roller bearing vibrations. J Sound Vib 165(3):455–466. doi:10.1006/jsvi.1993.1270

    Article  Google Scholar 

  26. Behzad M, Abbas RB, Mba David (2011) A new model for estimating vibrations generated in the defective rolling element bearings. J Vib Acoust 133(4):041011–041018. doi:10.1115/1.4003595

    Article  Google Scholar 

  27. Dolenc B, Boskosh P, Juricic D (2016) Distributed bearing fault diagnosis based on vibration analysis. Mech Syst Signal Process 66:521–532. doi:10.1016/j.ymssp.2015.06.007

    Article  Google Scholar 

  28. Cao M, Xiao J (2008) A comprehensive dynamic model of double-row spherical roller bearing-model development and case studies on surface defects, preloads, and radial clearance. Mech Syst Signal Process 22(2):467–489. doi:10.1016/j.ymssp.2007.07.007

    Article  Google Scholar 

  29. Harris TA (1984) Rolling bearing analysis. Wiley, Chichester

    Google Scholar 

  30. Choudhury A, Tandon N (2006) Vibration response of rolling element bearings in a rotor-bearing system to a local defect under radial load. J Tribol 128(2):252–261. doi:10.1115/1.2164467

    Article  Google Scholar 

  31. Eschmann P (1985) Ball and roller bearings: theory design and application. Wiley, New York

    Google Scholar 

Download references

Acknowledgements

This research did not receive any specific Grant from funding agencies in the public, commercial, or not-for-profit sectors.

Author information

Authors and Affiliations

  1. Sir Padampat Singhania University, Udaipur, 313601, India

    T. Govardhan & Achintya Choudhury

  2. Madhav University, Abu road, Sirohi, 307026, India

    Deepak Paliwal

Authors
  1. T. Govardhan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Achintya Choudhury
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Deepak Paliwal
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to T. Govardhan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Govardhan, T., Choudhury, A. & Paliwal, D. Vibration analysis of dynamically loaded bearing with distributed defect based on defect induced excitation. Int. J. Dynam. Control 6, 499–510 (2018). https://doi.org/10.1007/s40435-017-0324-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-017-0324-8

Keywords