Skip to main content
SpringerLink
Log in

Numerical investigation of influence sensitivity of a gas foil bearing parameters on the dynamic coefficients

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

Most studies on dynamic coefficients of bearings are focused on evaluation using different analytical methods. Minimal emphasis is given to the level of influence of each geometrical variable, the corresponding range of these variables for optimum stiffness and damping and the measure of performance of the analytical method used. The objective of this paper was to study the influence and sensitivity of length-to-diameter ratio, eccentricity ratio, bearing number, whirl ratio, and bearing compliance on the stiffness and damping of gas foil bearing. A numerical model is developed by utilizing the finite difference method to evaluate the dynamic coefficients. The results reveal that the normalized stiffness increases with the bearing number and decreases with increased bearing compliance whereas the normalized damping shows an opposite nature. Further, the stiffness coefficients tend to increase and the damping coefficients tend to decrease corresponding to increase in speed up to 240 krpm. The characteristic data sets obtained from the analysis is used to train an artificial neural network (ANN). Performance of ANN network is evaluated though computation of root-mean-square error (RSME) and regression coefficient (R2) and Mean Absolute Error (MAE). Utilizing the neural network results, a Sobol’s sensitivity test is carried out to identify most effective parameters which have a significant influence on the dynamic coefficients of gas foil bearing. After that, an adaptive neurofuzzy interface system (ANFIS) is established to determine the optimum range of data for which maximum stiffness and damping can be obtained. The results deduce that the neural network shows high efficacy in predicting the output variables correctly with a regression of more than 95%. It is also observed that the variation of dynamic coefficients is the highest for eccentricity ratio whereas lowest for whirl ratio. The maximum stiffness and damping coefficients are also obtained for a wide range of geometrical variables which can help in designing the gas foil bearing.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

Abbreviations

R :

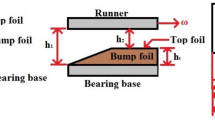
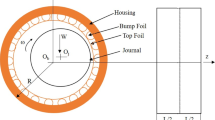
Radius of the journal (mm)

h :

Film thickness (mm)

h b :

Bump height (mm)

R b :

Bump radius (mm)

C :

Radial clearance (mm)

p :

Aerodynamic pressure (N/m 2)

s :

Pitch of bump (mm)

P :

Atmospheric pressure (N/m 2)

2 l :

Length of bump (mm)

E :

Young's modulus (N/m 2)

t b :

Bump foil thickness (mm)

\(\overline{p}\) :

Non-dimensional pressure (p/p a)

C :

Nominal bearing clearance (mm)

\(\overline{h}\) :

Non-dimensional film thickness (h/C)

\(\overline{t}\) :

Normalized time variable (ν t)

L/D :

Length-to-diameter ratio

\(\overline{h}_{0}\) , \(\overline{h}_{x}\) , \(\overline{h}_{y}\) , \(\overline{h}_{{\mathop 0\limits^{.} }}\) , \(\overline{h}_{{\mathop x\limits^{.} }}\) , \(\overline{h}_{{\mathop y\limits^{.} }}\) :

Perturbation components of \(\overline{h}\)

Δ x, Δ y :

Normalized perturbations

\(\overline{p}_{0}\) , \(\overline{p}_{x}\) , \(\overline{p}_{y}\) , \(\overline{p}_{{\mathop 0\limits^{.} }}\) , \(\overline{p}_{{\mathop x\limits^{.} }}\) , \(\overline{p}_{{\mathop y\limits^{.} }}\) :

Perturbation components of \(\overline{p}\)

\(\overline{K}_{mn}\) :

Normalized stiffness of bearing (\(c\overline{K}_{mn} /p_{a} R^{2}\))

\(\overline{C}_{mn}\) :

Normalized damping of bearing (\(c\omega \overline{C}_{mn} /p_{a} R^{2}\))

\(\overline{k}\) :

Normalized stiffness of the foundation (\(kc/p_{a}\))

\(\overline{u}\) :

Normalized foil deflection (u/c)

\(F_{x}\) , \(F_{y}\) :

Resultant forces in x and y directions

\(\overline{W}\) :

Normalized bearing load (\(W/p_{a} R^{2}\))

\(\overline{z}\) :

Normalized axial coordinate

θ :

Circumferential coordinate

Α :

Compliance number (\(p_{a} /ck\))

γ :

Whirl frequency ratio (ν/ω)

Λ :

Bearing number (\(6\mu \omega R^{2} /p_{a} c^{2}\))

Ε:

Eccentricity ratio

μ :

Lubricant viscosity

ν :

Whirl frequency

ω :

Rotor angular velocity

MLP:

Multi-layer perceptron

MF:

Membership function

MAE:

Mean absolute error

RMSE:

Root-mean-squared error

References

  1. Peng J-P, Carpino M (1993) Calculation of stiffness and damping coefficients for elastically supported gas foil bearings. ASME J Tribol 115(1):20–27

    Article  Google Scholar 

  2. Pletcher RH, Tannehill JC, Anderson D (2012) Computational fluid mechanics and heat transfer. CRC press, pp 155–156

  3. Peng Z-C, Khonsari M (2004) Hydrodynamic analysis of compliant foil bearings with compressible air flow. J Trib 126(3):542–546

    Article  Google Scholar 

  4. Heshmat H, Walowit J, Pinkus O (1983) Analysis of gas-lubricated foil journal bearings. J Lubr Technol 105(4):647–655

    Article  Google Scholar 

  5. Kim D (2007) Parametric studies on static and dynamic performance of air foil bearings with different top foil geometries and bump stiffness distributions. J Trobol Trans ASME 129(2):354–364

    Article  Google Scholar 

  6. Paulsen BT, Morosi S, Santos IF (2011) Static, dynamic, and thermal properties of compressible fluid film journal bearings. Tribol Trans 54(2):282–299

    Article  Google Scholar 

  7. Howard SA et al (2001) Steady-state stiffness of foil air journal bearings at elevated temperatures. Tribol Trans 44(3):489–493

    Article  Google Scholar 

  8. Carpino M, Talmage G (2006) Prediction of rotor dynamic coefficients in gas lubricated foil journal bearings with corrugated sub-foils. Tribol Trans 49(3):400–409

    Article  Google Scholar 

  9. Lahmar M, Ellagoune S, Bou-Saïd B (2010) Elastohydrodynamic lubrication analysis of a compliant journal bearing considering static and dynamic deformations of the bearing liner. Tribol Trans 53(3):349–368

    Article  Google Scholar 

  10. Rao T et al (2000) An analytical approach to evaluate dynamic coefficients and nonlinear transient analysis of a hydrodynamic journal bearing. Tribol Trans 43(1):109–115

    Article  Google Scholar 

  11. Feng K, Guo Z (2014) Prediction of dynamic characteristics of a bump-type foil bearing structure with consideration of dynamic friction. Tribol Trans 57(2):230–241

    Article  Google Scholar 

  12. Larsen JS, Varela AC, Santos IF (2014) Numerical and experimental investigation of bump foil mechanical behaviour. Tribol Int 74:46–56

    Article  Google Scholar 

  13. Larsen JS, Santos IF (2015) Efficient solution of the non-linear Reynolds equation for compressible fluid using the finite element method. J Braz Soc Mech Sci Eng 37(3):945–957

    Article  Google Scholar 

  14. Rubio D, Andrés LS (2006) Bump-type foil bearing structural stiffness: experiments and predictions. J Eng Gas Turbines Power 128(3):653–660

    Article  Google Scholar 

  15. Lez Le Sb,Arghir M and Frene J (2007) A new bump-type foil bearing structure analytical model. in Turbo Expo: Power for Land, Sea, and Air

  16. Feng H, Jiang S, Ji A (2019) Investigations of the static and dynamic characteristics of water-lubricated hydrodynamic journal bearing considering turbulent, thermohydrodynamic and misaligned effects. Tribol Int 130:245–260

    Article  Google Scholar 

  17. Guo Z et al (2018) Measurement and prediction of nonlinear dynamics of a gas foil bearing supported rigid rotor system. Measurement 121:205–217

    Article  Google Scholar 

  18. Lai T et al (2018) Numerical and experimental studies on stability of cryogenic turbo-expander with protuberant foil gas bearings. Cryogenics 96:62–74

    Article  Google Scholar 

  19. Hassan MFB, Bonello P (2017) A neural network identification technique for a foil-air bearing under variable speed conditions and its application to unbalance response analysis. J Tribol 139(2):021501

    Article  Google Scholar 

  20. Qin P et al (2005) Dynamic analysis of hydrodynamic bearing–rotor system based on neural network. Int J Eng Sci 43(5–6):520–531

    Article  Google Scholar 

  21. Kumar M et al (2019) Experimental investigation and performance prediction of a cryogenic turboexpander using artificial intelligence techniques. Appl Therm Eng 162:114273

    Article  Google Scholar 

  22. Haykin S (2010) Neural networks and learning machines. Pearson Education, India

    Google Scholar 

  23. Kumar M et al (2019) Preliminary design, flow field, and thermal performance analysis of a helium turboexpander: a numerical approach. SN Appl Sci 1(11):1482

    Article  Google Scholar 

  24. Zhang XY et al (2015) Sobol sensitivity analysis: a tool to guide the development and evaluation of systems pharmacology models. CPT Pharmacomet Syst Pharmacol 4(2):69–79

    Article  Google Scholar 

  25. Sobol IM (2001) Global sensitivity indices for nonlinear mathematical models and their monte carlo estimates. Math Comput Simul 55(1–3):271–280

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, NIT Rourkela, Rourkela, Odisha, 769008, India

    Debanshu S. Khamari, Jitesh Kumar & Suraj K. Behera

Authors
  1. Debanshu S. Khamari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jitesh Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Suraj K. Behera
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Debanshu S. Khamari.

Ethics declarations

Conflict of interest

The authors declared that there is no conflict of interest to any person or organisation.

Additional information

Technical Editor: Daniel Onofre de Almeida Cruz.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khamari, D.S., Kumar, J. & Behera, S.K. Numerical investigation of influence sensitivity of a gas foil bearing parameters on the dynamic coefficients. J Braz. Soc. Mech. Sci. Eng. 43, 167 (2021). https://doi.org/10.1007/s40430-021-02874-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-021-02874-0

Keywords

Search

Navigation