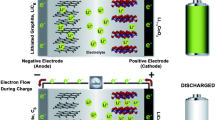
Abstract
Energy consumption with recovery of surplus production and availability at peak times is desirable for sustainable environments. The objective of the present paper is to plan storage systems based on battery banks in electrical distribution systems having distributed resources. In particular, wind-based power is considered, and the goal is to determine the quantity, location and capacity of batteries, as well as their operation conditions considering investment and operating costs. In this sense, a three-stage method is proposed. The first one determines candidate buses for battery allocation by applying a proposed sensitivity index that seeks to improve the quality and computational efficiency, obtained from an optimal power flow model. The second stage comprises a metaheuristic algorithm to optimize quantity and location of batteries and an optimal power flow to determine the batteries’ capacity, where the power injected or absorbed by batteries is modeled as an optimization variable. Finally, the optimal power flow of the third stage seeks to optimize the batteries and system operation. Four case studies are presented with different test systems. The proposed approach proved to be applicable for these systems, since it provides a reduction in the total planning and operating cost considering grid reliability and gives results that have good cost reduction from comparison with other solutions of literature. The main motivation is to show the applicability of a novel approach based on optimization procedure and sensitivity index to investigate issues that are relevant for planning storage systems in distribution networks.
















Similar content being viewed by others
Abbreviations
- \({\text{CSE}}\) :
-
Energy cost from the grid
- \({\text{CINEB}}\) :
-
Investment cost in battery energy storage capacity
- \({\text{CINPB}}\) :
-
Investment cost in battery power capacity
- \({\text{COM}}\) :
-
Operational and maintenance cost associated with battery systems
- \({\text{CONF}}\) :
-
Network reliability cost
- \({\text{CUE}}_{t}\) :
-
Unit cost of energy from the substation at time period \(t\), in $/kWh
- \({\text{PSE}}_{t}\) :
-
Power supplied by the substation at \(t\), in kW
- \(nb\) :
-
Number of system buses
- \(nh\) :
-
Number of time periods in a day
- \(ny\) :
-
Number of years in the planning horizon (25 years)
- \(ns\) :
-
Number of batteries
- \({\text{EBAT}}_{is}\) :
-
Nominal energy storage capacity of battery \(is\), in kWh
- \({\text{CINEB}}_{is}\) :
-
Unit cost related to the energy storage capacity of battery \(is\), in $/kWh
- \({\text{CINPB}}_{is}\) :
-
Unit cost for power capacity of battery \(is\), in $/kVA
- \({\text{SBA}}_{is,t}\) :
-
Power of battery \(is\) at time \(t\), in kVA
- \({\text{COM}}_{is}\) :
-
Operation and maintenance unit cost of battery \(is\), in $/kW
- \({\text{NA}}\) :
-
Number of distribution feeders
- \({\text{CENS}}_{ia}\) :
-
Cost of energy not supplied (ENS) in feeder \({ia}\)
- \(N_{ba}\) :
-
Number of buses supplied by feeder \(ia\)
- \(\lambda_{ib}\) :
-
Annual failure rate associated with bus \(ib\), in failure/year
- \({\text{FD}}_{ib}\) :
-
Damage function to clients at bus \(ib\)
- \({\text{CIR}}, {\text{CIC}}, {\text{CII}}\) :
-
Interruption costs for residential, commercial and industrial consumers, respectively, in $/kW
- \({\text{LR}}_{ib} ,{\text{LC}}_{ib} ,{\text{LI}}_{ib}\) :
-
Percentages of residential, commercial and industrial loads, respectively, at bus \(ib\)
- \(V_{{{\text{SE}},t}}\) :
-
Voltage of the EEDS substation at period \(t\)
- \(V_{{{\text{min}}}} ,V_{{{\text{max}}}}\) :
-
Lower and upper voltage limits, respectively
- \(V_{ib,t}\) :
-
Nodal voltage of bus \(ib\) at period \(t\)
- \({\text{PG}}_{ib,t} ,{\text{QG}}_{ib,t}\) :
-
Active and reactive powers, respectively, generated at bus \(ib\) and period \(t\) by non-distributed resources
- \(P_{ib,t}^{{{\text{wind}}}}\) :
-
Wind power at bus \(ib\) and period \(t\)
- \(P_{ib - m,t} ,Q_{ib - m,t}\) :
-
Active and reactive power flows, respectively, in section \(ib - m\), period \(t\)
- \({\Omega }ib\) :
-
Set of buses connected to bus \(ib\) through distribution branches
- \({\text{PBA}}_{is,t} ,{\text{QBA}}_{is,t}\) :
-
Active and reactive powers, respectively, developed by battery \(is\) at period \(t\)
- \(S_{ib}\) :
-
Set of batteries at bus \(ib\)
- \(P_{ib,t}^{{{\text{load}}}} ,Q_{ib,t}^{{{\text{load}}}}\) :
-
Active and reactive load demands, respectively, at bus \(ib\) and period \(t\)
- \(x_{ib}\) :
-
Integer variable related to the decision of battery allocation at bus \(ib\)
- \(x_{ib}^{*}\) :
-
Optimal values of \(x_{ib}\) from Stage 2;
- \(v_{t}\) :
-
Wind speed at period \(t\);
- \(\lambda p_{ib,t}\) :
-
Lagrange multiplier associated with the active power balance constraint of the OPF for bus \(ib\) and period \(t\);
- \({\text{SI}}_{ib}\) :
-
Sensibility index for bus \(ib\);
- \(E_{ib}\) :
-
Set of equipment connected to bus \(ib\)
- \(\lambda_{ie}\) :
-
Annual failure rate of equipment \(ie\)
- \({\text{SOC}}_{is,t}\) :
-
State of charge of battery \(is\) in period \(t\)
- \(\eta_{is,t}\) :
-
Operating efficiency of battery \(is\) at period \(t\)
- \(a_{is} ,b_{is}\) :
-
Recharging constants inherent to battery \(is\)
- \(I_{is,t}\) :
-
Current in terminals of battery \(is\) at period \(t\)
- \(I_{10}\) :
-
Battery rated discharge current
- \(it, it_{{{\text{max}}}} ,nt_{{{\text{est}}}}\) :
-
Generation counter, maximum number of generations and number of generations without improvement in the best solution of the AIS algorithm
References
Abedinia, O., Zareinejad, M., Doranehgard, M. H., Fathi, G., & Ghadimi, N. (2019). Optimal offering and bidding strategies of renewable energy based large consumer using a novel hybrid robust-stochastic approach. Journal of Cleaner Production, 215, 878–889. https://doi.org/10.1016/j.jclepro.2019.01.085
Achaibou, N., Haddadi, M., & Malek, A. (2012). Modeling of lead acid batteries in PV systems. Energy Procedia, 18, 538–544
Aghajani, G., & Ghadimi, N. (2018). Multi-objective energy management in a micro-grid. Energy Reports, 4, 218–225. https://doi.org/10.1016/j.egyr.2017.10.002
Akbary, P., Ghiasi, M., Pourkheranjani, M. R. R., Alipour, H., & Ghadimi, N. (2019). Extracting appropriate nodal marginal prices for all types of committed reserve. Computational Economics, 53(1), 1–26. https://doi.org/10.1007/s10614-017-9716-2
Bignucolo, F., Caldon, R., & Prandoni, V. (2008). Radial MV networks voltage regulation with distribution management system coordinated controller. Electric Power Systems Research, 78(4), 634–645
Cao, M., Xu, Q., Qin, X., & Cai, J. (2020). Battery energy storage sizing based on a model predictive control strategy with operational constraints to smooth the wind power. International Journal of Electrical Power and Energy Systems, 115, 105471. https://doi.org/10.1016/j.ijepes.2019.105471
Carrano, E. G., Guimarães, F. G., Takahashi, R. H. C., Neto, O. M., & Campelo, F. (2007). Electric distribution network expansion under load-evolution uncertainty using an immun system inspired algorithm. IEEE Transactions on Power Systems, 22(2), 851–861. https://doi.org/10.1109/TPWRS.2007.894847
Carrano, E. G., Soares, L. A., Takahashi, R. H., Saldanha, R. R., & Neto, O. M. (2006). Electric distribution network multiobjective design using a problem-specific genetic algorithm. IEEE Transactions on Power Delivery, 21(2), 995–1005. https://doi.org/10.1109/TPWRD.2005.858779
Choe, J. M., Cho, Y., & Choe, G. H. (2014). Standalone ESS modeling and dual-loop control using Zn-Br redox flow battery. In 2014 IEEE Energy Conversion Congress and Exposition (ECCE) IEEE. https://doi.org/10.1109/ECCE.2014.6954130
da Silva Seta, F., de Oliveira, L. W., & de Oliveira, E. J. (2019). Comprehensive approach for distribution system planning with uncertainties. IET Generation, Transmission & Distribution, 13(24), 5467–5477
de Castro, L. N., & Von Zuben, F. J. (2002). Learning and optimization using the clonal selection principle. IEEE transactions on evolutionary computation, 6(3), 239–251
de Oliveira, L. W., de Oliveira, E. J., Gomes, F. V., Silva, I. C., Jr., Marcato, A. L., & Resende, P. V. (2014). Artificial immune systems applied to the reconfiguration of electrical power distribution networks for energy loss minimization. International Journal of Electrical Power & Energy Systems, 56, 64–74
de Oliveira, L. W., Seta, F. D. S., & De Oliveira, E. J. (2016). Optimal reconfiguration of distribution systems with representation of uncertainties through interval analysis. International Journal of Electrical Power and Energy Systems, 83, 382–391. https://doi.org/10.1016/j.ijepes.2016.04.020
Diniz, A. L., Costa, F. D. S., Maceira, M. E., dos Santos, T. N., Dos Santos, L. C. B., & Cabral, R. N. (2018). Short/mid-term hydrothermal dispatch and spot pricing for large-scale systems-the case of Brazil. In: 2018 Power Systems Computation Conference (PSCC) (pp. 1–7). IEEE. https://doi.org/10.23919/PSCC.2018.8442897
Elkazaz, M., Sumner, M., Davies, R., Pholboon, S., & Thomas, D. (2019). Optimization based real-rime home energy management in the presence of renewable energy and battery energy storage. In: 2019 International Conference on Smart Energy Systems and Technologies (SEST) (pp. 1–6). IEEE. https://doi.org/10.1109/SEST.2019.8849105
El-Khattam, W., Hegazy, Y. G., & Salama, M. M. A. (2005). An integrated distributed generation optimization model for distribution system planning. IEEE Transactions on power systems, 20(2), 1158–1165
Falaghi, H., Singh, C., Haghifam, M. R., & Ramezani, M. (2011). DG integrated multistage distribution system expansion planning. International Journal of Electrical Power and Energy Systems, 33(8), 1489–1497. https://doi.org/10.1016/j.ijepes.2011.06.031
Fosso, O. B., Gjelsvik, A., Haugstad, A., Mo, B., & Wangensteen, I. (1999). Generation scheduling in a deregulated system. The norwegian case. IEEE Transactions on Power Systems, 14(1), 75–80. https://doi.org/10.1109/59.744487
Ghatak, S. R., Sannigrahi, S., & Acharjee, P. (2019). Multi-objective approach for strategic incorporation of solar energy source, battery storage system, and DSTATCOM in a smart grid environment. IEEE Systems Journal, 13(3), 3038–3049. https://doi.org/10.1109/JSYST.2018.2875177
Hamian, M., Darvishan, A., Hosseinzadeh, M., Lariche, M. J., Ghadimi, N., & Nouri, A. (2018). A framework to expedite joint energy-reserve payment cost minimization using a custom-designed method based on mixed integer genetic algorithm. Engineering Applications of Artificial Intelligence, 72, 203–212. https://doi.org/10.1016/j.engappai.2018.03.022
Hong, Y. Y., & Wu, M. Y. (2019). Markov model-based energy storage system planning in power systems. IEEE Systems Journal, 13(4), 4313–4323. https://doi.org/10.1109/JSYST.2019.2900081
Karmarkar, N. K., & Ramakrishnan, K. G. (1991). Computational results of an interior point algorithm for large scale linear programming. Mathematical Programming, 52(1), 555–586
Kelly, J. J., & Leahy, P. G. (2019). Sizing battery energy storage systems: Using multi-objective optimisation to overcome the investment scale problem of annual worth. IEEE Transactions on Sustainable Energy, 11(4), 2305–2314. https://doi.org/10.1109/TSTE.2019.2954673
Khaki, B., & Das, P. (2019). Sizing and Placement of Battery Energy Storage Systems and Wind Turbines by Minimizing Costs and System Losses. arXiv preprint arXiv:1903.12029.
Khodaei, H., Hajiali, M., Darvishan, A., Sepehr, M., & Ghadimi, N. (2018). Fuzzy-based heat and power hub models for cost-emission operation of an industrial consumer using compromise programming. Applied Thermal Engineering, 137, 395–405. https://doi.org/10.1016/j.applthermaleng.2018.04.008
Lehtola, T., & Zahedi, A. (2019). Solar energy and wind power supply supported by storage technology: A review. Sustainable Energy Technologies and Assessments, 35, 25–31. https://doi.org/10.1016/j.seta.2019.05.013
Leng, H., Li, X., Zhu, J., Tang, H., Zhang, Z., & Ghadimi, N. (2018). A new wind power prediction method based on ridgelet transforms, hybrid feature selection and closed-loop forecasting. Advanced Engineering Informatics, 36, 20–30. https://doi.org/10.1016/j.aei.2018.02.006
Li, J. (2019). Optimal sizing of grid-connected photovoltaic battery systems for residential houses in Australia. Renewable Energy, 136, 1245–1254. https://doi.org/10.1016/j.renene.2018.09.099
Liu, Y., Wang, W., & Ghadimi, N. (2017). Electricity load forecasting by an improved forecast engine for building level consumers. Energy, 139, 18–30. https://doi.org/10.1016/j.energy.2017.07.150
Mirzapour, F., Lakzaei, M., Varamini, G., Teimourian, M., & Ghadimi, N. (2019). A new prediction model of battery and wind-solar output in hybrid power system. Journal of Ambient Intelligence and Humanized Computing, 10(1), 77–87. https://doi.org/10.1007/s12652-017-0600-7
Moraes, H. F., Trentini, C., Oliveira, L. W., Dias, B. H., & Ferreira, V. H. (2017). Optimization of the maintenance programs of distribution systems with focus on the reliability through an artificial immune system. In: Proceedings of the 12th Latin-American Congress on Eletricity Generation and Transmission, Mar del Plata, Argentina.
N’guessan, S. A., Agbli, K. S., Fofana, S., & Hissel, D. (2020). Optimal sizing of a wind, fuel cell, electrolyzer, battery and supercapacitor system for off-grid applications. International Journal of Hydrogen Energy, 45(8), 5512–5525. https://doi.org/10.1016/j.ijhydene.2019.05.212
Naderi, E., Kiaei, I., & Haghifam, M. R. (2010). NaS technology allocation for improving reliability of DG-enhanced distribution networks. In: 2010 IEEE 11th International Conference on Probabilistic Methods Applied to Power Systems (pp. 148–153). IEEE. https://doi.org/10.1109/PMAPS.2010.5528990
Nakatsuji-Mather, M., & Saha, T. K. (2012). Zinc-bromine flow batteries in residential electricity supply Two case studies. In 2012 IEEE Power and Energy Society General Meeting, IEEE. https://doi.org/10.1109/PESGM.2012.6344777
Nian, V., Jindal, G., & Li, H. (2019). A feasibility study on integrating large-scale battery energy storage systems with combined cycle power generation – Setting the bottom line. Energy, 185, 396–408. https://doi.org/10.1016/j.energy.2019.07.028
Ogunjuyigbe, A. S. O., Ayodele, T. R., & Akinola, O. A. (2016). Optimal allocation and sizing of PV/Wind/Split-diesel/Battery hybrid energy system for minimizing life cycle cost, carbon emission and dump energy of remote residential building. Applied Energy, 171, 153–171
Sedghi, M., Ahmadian, A., & Aliakbar-Golkar, M. (2015). Optimal storage planning in active distribution network considering uncertainty of wind power distributed generation. IEEE Transactions on Power Systems, 31(1), 304–316. https://doi.org/10.1109/TPWRS.2015.2404533
Shang, C., Srinivasan, D., & Reindl, T. (2016). Generation-scheduling-coupled battery sizing of stand-alone hybrid power systems. Energy, 114, 671–682
Sufyan, M., Rahim, N. A., Aman, M. M., Tan, C. K., & Raihan, S. R. S. (2019). Sizing and applications of battery energy storage technologies in smart grid system: A review. Journal of Renewable and Sustainable Energy, 11(1), 014105. https://doi.org/10.1063/1.5063866
Vigano, G., Rossi, M., Moneta, D., & Carlini, C. (2015). Methodology for the optimal siting and sizing of storage systems in distribution networks. In: 2015 AEIT International Annual Conference (AEIT) (pp. 1–6). IEEE. https://doi.org/10.1109/AEIT.2015.7415231
Wong, L. A., Ramachandaramurthy, V. K., Walker, S. L., Taylor, P., & Sanjari, M. J. (2019). Optimal placement and sizing of battery energy storage system for losses reduction using whale optimization algorithm. Journal of Energy Storage, 26, 100892. https://doi.org/10.1016/j.est.2019.100892
Wu, D., Jin, C., Balducci, P., & Kintner-Meyer, M. (2015). An energy storage assessment: Using optimal control strategies to capture multiple services. In 2015 IEEE Power & Energy Society General Meeting (pp. 1–5). IEEE. https://doi.org/10.1109/PESGM.2015.7285820
Yamchi, H. B., Shahsavari, H., Kalantari, N. T., Safari, A., & Farrokhifar, M. (2019). A cost-efficient application of different battery energy storage technologies in microgrids considering load uncertainty. Journal of Energy Storage, 22, 17–26. https://doi.org/10.1016/j.est.2019.01.023
Yuasa, K., Omura, I., Ueshima, M., & Babasaki, T. (2019). Power energy cost reduction effects by applying optimized long-term storage battery operation strategy. In: 2019 8th International Conference on Renewable Energy Research and Applications (ICRERA) (pp. 107–112). IEEE. https://doi.org/10.1109/ICRERA47325.2019.8996953
Zhang, Y., Dong, Z. Y., Luo, F., Zheng, Y., Meng, K., & Wong, K. P. (2016). Optimal allocation of battery energy storage systems in distribution networks with high wind power penetration. IET Renewable Power Generation, 10(8), 1105–1113. https://doi.org/10.1049/iet-rpg.2015.0542
Author information
Authors and Affiliations
Corresponding author
Appendix A: Type of Consumers
Rights and permissions
About this article
Cite this article
de Oliveira, L.W., de Oliveira, J.G., Dias, B.H. et al. Optimal Allocation of Battery in Electrical Distribution Systems with Distributed Resources. J Control Autom Electr Syst 32, 1289–1304 (2021). https://doi.org/10.1007/s40313-021-00732-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40313-021-00732-x