Mathematical modeling and fuzzy availability analysis for serial processes in the crystallization system of a sugar plant

Abstract

The binary states, i.e., success or failed state assumptions used in conventional reliability are inappropriate for reliability analysis of complex industrial systems due to lack of sufficient probabilistic information. For large complex systems, the uncertainty of each individual parameter enhances the uncertainty of the system reliability. In this paper, the concept of fuzzy reliability has been used for reliability analysis of the system, and the effect of coverage factor, failure and repair rates of subsystems on fuzzy availability for fault-tolerant crystallization system of sugar plant is analyzed. Mathematical modeling of the system is carried out using the mnemonic rule to derive Chapman–Kolmogorov differential equations. These governing differential equations are solved with Runge–Kutta fourth-order method.

Introduction

The binary state assumption in conventional reliability theory is not extensively acceptable in various engineering problems. Since 1965, a higher importance in scientific environment has been given to fuzzy theory by Zadeh (1965), when he presented the basic concepts of fuzzy set theory. This has changed the basic scenario in reliability and concerned theories, because this theory can handle all the possible states that lie between a fully working state and a completely failed state. Thus, binary state assumption used in conventional reliability is replaced by fuzzy state assumption and this approach to the reliability is known as profust reliability. Though conventional reliability theory cannot be ignored, fuzzy reliability theory also needs to be considered along with it. The availability and reliability are the important performance parameters for industrial systems such as sugar mill, chemical industry, thermal power plant, paper plant, etc., and have major importance in real life situations, as the demand for product quality and system reliability has been increasing day by day.

This paper is organized as follows. The present section is the introductory type. Section 2 is concerned with materials and methods used, while Sect. 3 deals with the literature review. Section 4 is related with system description, notations and assumptions. Section 5 is devoted to mathematical modeling of the system. Section 6 is concerned with performance analysis of the system. Finally, some concrete conclusions have been presented in Sect. 7.

Materials and methods

Failure rate

The constant failure rate (β) is the ratio of the number of failures of a component in a given time to the total period of time the component was operating. It is expressed as the number of failures per unit hour.

Repair rate

The constant repair rate (µ) is the ratio of the number of repairs of a component in a given time to the total period of time the component was being repaired. It is expressed as the number of repairs per unit hour.

Fuzzy availability

Kumar and Kumar (2011) stated a fuzzy probabilistic semi-Markov model {(S _n, T _n), n € N} consisting of ‘n’ states together with transition time.

Let U = {S ₁, S ₂,…,S _n} denote the universe of discourse. On this universe, we define a fuzzy success state S, $S = \left\{ {(S_{\text{i}} , \, \mu_{\text{s}} \left( {S_{\text{i}} } \right); \, i {\kern 1pt} = {\kern 1pt} 1,2,3, \ldots ,n} \right\},$ and a fuzzy failure state F,

$$ F = \left\{ {(S{\text{i}}, \, \mu_{\text{F}} \left( {S_{\text{i}} } \right); \, i = 1,2,3, \ldots ,n} \right\}, $$

where µ _s (S _i) and µ _F (S _i) are trapezoidal fuzzy numbers, respectively. The fuzzy availability of the crystallization system is defined as;

$$ A({\text{t}}) = \sum\limits_{1}^{6} {\mu {\text{s}}\, (S{\text{i)}}\,P{\text{i(}}t)} . $$

Fault-tolerant system

A system is known to be fault tolerant, if it can tolerate some faults and function successfully even in the presence of these faults. It is generally achieved by using redundancy concepts. Automatic recovery and reconfiguration mechanism (detection, location and isolation) plays a crucial role in implementing fault tolerance, because an uncovered fault may lead to a system or subsystem failure even when adequate redundancy exists. Hence, a system subjected to imperfect fault coverage (also known as coverage factor) may fail prior to the exhaustion of redundancy due to uncovered component failures.

Coverage factor

Kumar and Kumar (2011) stated that the probability of successful reconfiguration operation of a fault-tolerant system is defined as a coverage factor. It is denoted by ‘c’ and if its value is less than 1, then it is known as imperfect coverage. Ram et al. (2013) defined the coverage factor as the conditional probability of recovery, given that a fault has occurred. The coverage factor is one of the most important aspects to take into account in design, management and evaluation of fault-tolerant systems.

Markov process

The continuous-time discrete-state Markov process models are used for describing the behavior of repairable systems in reliability studies as stated by Dhillion and Singh (1981) and Balaguruswamy (1984). The birth-and-death process is a special case of continuous-time Markov process; it is characterized by the birth rate (μ) and death rate (β) and it is assumed that the birth-and-death events are independent of each other. When a birth, i.e., repair occurs, the process goes from state i to state i + 1. Similarly, when death, i.e., failure occurs, the process goes from state i to state i−1.

According to Markov, if P ₁(t) represents the probability of zero occurrences in time t, the probability of zero occurrences in time (t + Δt) is given by the equation

$$ P_{ 1} \left( {t + \Delta {\text{t}}} \right)\; = \;\left( { 1- \beta {\text{t}}} \right) \, P_{ 1} \left( {\text{t}} \right). $$

(i)

Similarly,

$$ P_{ 2} \left( {t + \Delta {\text{t}}} \right)\; = \;\mu \Delta {\text{t }}P_{ 1} \left( {\text{t}} \right)\; + \;\left( { 1- \beta \Delta {\text{t}}} \right)P_{ 2} \left( {\text{t}} \right). $$

(ii)

The equation (ii) shows that the probability of one occurrence in time (t + Δt) is composed of two units:

• (i) probability of zero occurrences in time t multiplied by the probability of one occurrence in time interval ∆t and

• (ii) probability of one occurrence in time t multiplied by the probability of no occurrences in the interval ∆t.

Literature review

The performance of an industrial system can be measured using several techniques as mentioned in the literature. Some of the techniques which are widely used are: event tree, fault tree analysis (FTA), reliability block diagrams (RBDs), Petri nets (PNs) and Markovian approach, as stated by Garg and Sharma (2012) and Renganathan and Bhaskar (2011). Garg and Sharma (2011) used the concept of fuzzy set theory to represent the failure and repair data and analyzed the behavior of the system using various reliability indices. These indices include failure rate, repair time, mean time between failures (MTBF), expected number of failures (ENOF) and availability and reliability of the system. Kumar et al. (2007) analyzed the reliability of a non-redundant robot using fuzzy lambda–tau methodology. Singer (1990) developed a new methodology to find out various reliability parameters using fuzzy set approach and fault tree in which the failure rate and repair time were represented using triangular fuzzy numbers (TFN). Cheng and Mon (1993) used the confidence interval for analyzing the fuzzy system reliability. Chen (1994) presented a new method for analyzing system reliability using fuzzy number arithmetic operations. Knezevic and Odoom (2001) proposed a new methodology by making use of Petri nets (PNs) instead of fault trees. Arora and Kumar (1997) analyzed the availability for the coal handling system in the paper plant. Biswas and Sarkar (2000) studied the availability of a system maintained through several imperfect repairs before a replacement or a perfect repair. Jain (2003) discussed the N-policy for a redundant repairable system with an additional repairman. Singh et al. (2005) analyzed a three-unit standby system of water pumps in which two units were operative simultaneously and the third one was a cold standby for an ash handling plant. You and Chen (2005) proposed an efficient heuristic approach for series–parallel redundant reliability problems. Cheng and Mon (1993) presented a method for fuzzy system reliability analysis by interval of confidence. Chen (1994) presented a method for fuzzy system reliability analysis using fuzzy number arithmetic operations. Cai (1996) stated that the fuzzy reliability can be physically interpreted as the probability that no substantial performance deterioration occurs in a predefined time interval. Chen (2003) presented a new method for analyzing the fuzzy system reliability based on vague sets. Taheri and Zarei (2011) investigated the Bayesian system reliability assessment in a vague environment. Kumar and Yadav (2012) analyzed the fuzzy system reliability using different types of intuitionistic fuzzy numbers (IFNs) instead of the classical probability distribution for the components. Blischke and Murthy (2003) suggested that the failure of the component or system cannot be prevented completely, but can be minimized. Sharma and Khanduja (2013) discussed the performance evaluation and availability analysis of a feeding system of a sugar plant. Dhople et al. (2014) proposed a framework to analyze the Markov reward models, which are commonly used in the system performability analysis. Doostparast et al. (2014) planned a reliability-based periodic preventive maintenance (PM) for a system with deteriorating components. Shakuntla et al. (2011) discussed the availability analysis for a pipe manufacturing industry using supplementary variable technique. Katherasan et al. (2013) optimized the welding parameters for the flux cored arc welding process using the genetic algorithm and simulated annealing. Natarajan et al. (2013) proposed a model that would facilitate the infusing of quality and reliability in new products by blending the six sigma concept and the new product development (NPD) process. Yuan and Meng (2011) assumed the exponential distribution of working and repair time for a warm standby repairable system consisting of two dissimilar units and one repairman. Zhang and Mostashari (2011) proposed a method to assess the reliability of the system with continuous distribution of component states. This method is useful when we do not have enough knowledge on the component states and related probabilities. Zoulfaghari et al. (2014) presented a new mixed integer nonlinear programming (MINLP) model to analyze the availability optimization of a system with a given structure, using both repairable and non-repairable components simultaneously.

The literature revealed that the methods used by the authors involve complex computations, and the problem of determining long-run availability and reliability of the system based on conventional reliability has been extensively studied in the literature. In this paper, an advance numerical method, i.e., Runge–Kutta fourth-order method is used for fuzzy availability analysis for the crystallization system of a sugar plant. The required data are collected from the maintenance history sheets and by discussion with the maintenance personnel of the sugar plant situated at South of Haryana, India.

In the process of manufacturing of sugar, initially the sugarcane is fed through the conveyor and cutters to cut into small pieces. These small pieces of sugarcane are passed through the crushing system to get raw sugarcane juice and bagasse is left for the feeder or fodder. The process of refining raw sugarcane juice is performed as it contains fibers, mud and other impurities. The mud present in the sugarcane juice is separated by the sulfonation process, while the soluble and insoluble impurities present in the cane juice get further separated by heating the cane juice in boilers to about 68 °C. The juice gets concentrated by further heating to about 102 °C. The crystalline sugar is obtained from the concentrated juice by the crystallization process. The sugar plant comprises large complex engineering systems arranged in series or parallel, or a combination of both. Some of these systems are for feeding, crushing, refining, evaporation, steam generation, crystallization, etc., in which the crystallization system is one of the most important.

System description, notations and assumptions

System description

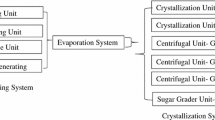
The crystallization system comprises the following three subsystems with series or parallel configurations as shown in Fig. 1.

Fig. 1

Schematic flow diagram of the crystallization system of a sugar plant with standby units

• (i) Subsystem A (crystallization): It consists of two units connected in parallel, one operative and the other in a cold standby state. The complete failure of the system will occur when more than one unit fail at a time.

• (ii) Subsystem B (centrifugal pump): It consists of three units connected in parallel and complete failure of the system will occur when more than two units fail at a time.

• (iii) Subsystem C (sugar grader unit): It consists of a single unit connected in series. The complete failure of the system will occur when this subsystem fails at a time.

Notations

: Indicates that the system is in a full working state.

: Indicates that the system is in a standby state.

: Indicates that the system is in a failed state.

A, B and C :

Indicates full working states of subsystems

A ₁, B ₁ and B ₂ :

Indicates that the subsystems A and B are working under cold standby states

a, b and c :

Indicates the failed states of subsystems A, B and C, respectively

β _i = 1,2,3…6:

The constant failure rate of subsystems A, A₁, B, B₁, B₂ and C, respectively

µ _i = 1, 2,3…6:

The constant repair rate of subsystems A, A₁, B, B₁, B₂ and C, respectively

c :

Coverage factor (its value lies between 0 and 1)

P ₁, P ₂, P ₃, P ₄, P ₅ and P ₆ :

Fuzzy availability of the system under states 1, 2, 3, 4, 5 and 6, respectively

P _j (t), j = 1, 2, 3…17:

The probability that the system is in the jth state at time t and p′ represents its derivative with respect to time (t).

Assumptions

• The failure and repair rates are statistically independent of each other and there are no simultaneous failures among the subsystems as stated by Sharma and Khanduja (2013).

• There are sufficient repair or replacement facilities and a repaired system is as good as new, performance-wise, as stated by Ebeling (2001).

Mathematical modeling of the system

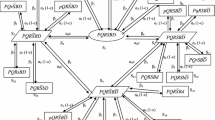
The mathematical modeling of the crystallization system is carried out using the mnemonic rule for the three subsystems and the Chapman–Kolmogorov differential equations are developed. According to this rule, the derivative of the probability of every state is equal to the sum of all probability flows which comes from other states to the given state minus the sum of all probability flows which goes out from the given state to the other states. The transition diagram (Fig. 2) depicts a simulation model showing all the possible states of the feeding system.

Fig. 2

Transition diagram of the crystallization system of a sugar plant

State 1:

The system is working with full capacity (with no standby)

State 2:

The system is working with a standby unit of crystallization (A ₁)

State 3:

The system is working with a standby unit of a centrifugal pump (B ₁)

State 4:

The system is working with a standby unit of crystallization and a centrifugal pump (A ₁ and B ₁)

State 5:

The system is working with a standby unit of a centrifugal pump (B ₂)

State 6:

The system is working with standby units of crystallization (A₁) and centrifugal pump (B ₂)

State 7 to 17:

Failed states of the system due to complete failure of its subsystems, i.e., A, B and C

The equations for fuzzy availability for the crystallization system are derived as follows.

The mathematical Eqs. (1) to (17) are developed for each state, one by one, for 17 states of the transition diagram (Fig. 2).

$$ P^\prime_{ 1} \left( {\text{t}} \right)\;\; = \;\; - \, X_{ 1} P_{ 1} \left( {\text{t}} \right)\; + \;\mu_{ 1} P_{ 2} \left( {\text{t}} \right)\; + \;\mu_{ 3} P_{ 3} \left( {\text{t}} \right)\; + \;\mu_{ 6} P_{ 1 5} \left( {\text{t}} \right), $$

(1)

$$ P^\prime_{ 2} \left( {\text{t}} \right)\; = \; - \, X_{ 2} P_{ 2} \left( {\text{t}} \right)\; + \;\beta_{ 1} {\text{c}}P_{ 1} \left( {\text{t}} \right)\; + \, \mu_{ 2} P_{ 1 3} \left( {\text{t}} \right)\; + \;\mu_{ 3} P_{ 4} \left( {\text{t}} \right)\,\; + \;\mu_{ 6} P_{ 1 4} \left( {\text{t}} \right), $$

(2)

$$ P^\prime_{ 3} \left( {\text{t}} \right)\; = \; - X_{ 3} P_{ 3} \left( {\text{t}} \right)\; + \;\mu_{ 1} P_{ 4} \left( {\text{t}} \right)\; + \;\beta_{ 3} cP_{ 1} \left( {\text{t}} \right)\; + \;\mu_{ 4} P_{ 5} \left( {\text{t}} \right)\; + \;\mu_{ 6} P_{ 1 6} \left( {\text{t}} \right), $$

(3)

$$ P^\prime_{ 4} \left( {\text{t}} \right)\; = \; - X_{ 4} P_{ 4} \left( {\text{t}} \right)\; + \;\beta_{ 1} cP_{ 3} \left( {\text{t}} \right)\; + \;\mu_{ 1} P_{ 1 1} \left( {\text{t}} \right)\; + \;\beta_{ 3} cP_{ 2} \left( {\text{t}} \right)\; + \;\mu_{ 4} P_{ 6} \left( {\text{t}} \right)\; + \;\mu_{ 6} P_{ 1 2} \left( {\text{t}} \right), $$

(4)

$$ P^\prime_{ 5} \left( {\text{t}} \right)\; = \;\; - X_{ 5} P_{ 5} \left( {\text{t}} \right)\; + \;\mu_{ 1} P_{ 6} \left( {\text{t}} \right)\; + \;\beta_{ 4} {\text{c}}P_{ 3} \left( {\text{t}} \right)\; + \;\mu_{ 5} P_{ 7} \left( {\text{t}} \right)\; + \;\mu_{ 6} P_{ 1 7} \left( {\text{t}} \right), $$

(5)

$$ P^\prime_{ 6} \left( {\text{t}} \right)\; = \; - \, X_{ 6} P_{ 6} \left( {\text{t}} \right)\; + \;\beta_{ 1} {\text{c}}P_{ 5} \left( {\text{t}} \right)\; + \;\mu_{ 1} P_{ 10} \left( {\text{t}} \right)\; + \;\beta_{ 4} {\text{c}}P_{ 4} \left( {\text{t}} \right)\; + \;\mu_{ 5} P_{ 8} \left( {\text{t}} \right)\; + \;\mu_{ 6} P_{ 9} \left( {\text{t}} \right), $$

(6)

where

X ₁ = β ₁c + β ₃c + β ₆(1−c),

X ₂ = µ ₁ + β ₂(1−c) + β ₃c +β ₆(1−c),

X ₃ = β ₁c + µ ₃ + β ₄c + β ₆(1−c),

X ₄ = µ ₁ + β ₁(1−c) + µ ₃ + β ₄c + β ₆(1−c),

X ₅ = β ₁c + µ ₄ + β ₅(1−c) + β ₆(1−c),

X ₆ = µ ₁ + β ₂(1−c) + µ ₄ + β ₅(1−c) + β ₆(1−c).

Similarly,

$$ P^\prime_{ 7} \left( {\text{t}} \right)\; + \;\mu_{ 5} P_{ 7} \left( {\text{t}} \right)\; = \;\;\beta_{ 5} \left( { 1- {\text{c}}} \right)P_{ 5} \left( {\text{t}} \right), $$

(7)

$$ P^\prime_{ 8} \left( {\text{t}} \right)\; + \, \mu_{ 5} P_{ 8} \left( {\text{t}} \right)\; = \;\beta_{ 5} \left( { 1- {\text{c}}} \right)P_{ 6} \left( {\text{t}} \right), $$

(8)

$$ P^\prime_{ 9} \left( {\text{t}} \right)\; + \;\mu_{ 6} P_{ 9} \left( {\text{t}} \right)\; = \; \, \beta_{ 6} \left( { 1- {\text{c}}} \right)P_{ 6} \left( {\text{t}} \right), $$

(9)

$$ P^\prime_{ 10} \left( {\text{t}} \right)\; + \;\mu_{ 1} P_{ 10} \left( {\text{t}} \right)\; = \;\beta_{ 1} \left( { 1- {\text{c}}} \right)P_{ 6} \left( {\text{t}} \right), $$

(10)

$$ P^\prime_{ 1 1} \left( {\text{t}} \right)\; + \;\mu_{ 1} P_{ 1 1} \left( {\text{t}} \right)\; = \;\beta_{ 1} \left( { 1- {\text{c}}} \right)P_{ 4} \left( {\text{t}} \right), $$

(11)

$$ P^\prime_{ 1 2} \left( {\text{t}} \right)\; + \;\mu_{ 6} P_{ 1 2} \left( {\text{t}} \right)\; = \;\beta_{ 6} \left( { 1- {\text{c}}} \right)P_{ 4} \left( {\text{t}} \right), $$

(12)

$$ P^\prime_{ 1 3} \left( {\text{t}} \right)\; + \;\mu_{ 2} P_{ 1 3} \left( {\text{t}} \right)\; = \;\beta_{ 2} \left( { 1- {\text{c}}} \right)P_{ 2} \left( {\text{t}} \right), $$

(13)

$$ P^\prime_{ 1 4} \left( {\text{t}} \right)\; + \;\mu_{ 6} P_{ 1 4} \left( {\text{t}} \right)\; = \;\beta_{ 6} \left( { 1- {\text{c}}} \right)P_{ 2} \left( {\text{t}} \right), $$

(14)

$$ P^\prime_{ 1 5} \left( {\text{t}} \right)\; + \;\mu_{ 6} P_{ 1 5} \left( {\text{t}} \right)\; = \;\beta_{ 6} \left( { 1- {\text{c}}} \right)P_{ 1} \left( {\text{t}} \right), $$

(15)

$$ P^\prime_{ 1 6} \left( {\text{t}} \right)\; + \;\mu_{ 6} P_{ 1 6} \left( {\text{t}} \right)\; = \;\beta_{ 6} \left( { 1- {\text{c}}} \right)P_{ 3} \left( {\text{t}} \right), $$

(16)

$$ P^\prime_{ 1 7} \left( {\text{t}} \right)\; + \;\mu_{ 6} P_{ 1 7} \left( {\text{t}} \right)\; = \;\beta_{ 6} \left( { 1- {\text{c}}} \right)P_{ 5} \left( {\text{t}} \right), $$

(17)

with initial conditions:

$$ P_{\text{j}} (0)\; = \;\left\{ \begin{array}{*{20}c}1 ,\, {\text{if }}j = 1 \\ 0,\, {\text{if }}j \ne 1 \\ \end{array} \right.. $$

(18)

The system of differential Eqs. (1) to (17) with initial conditions given by Eq. (18) was solved by the Runge–Kutta fourth-order method. The numerical computations were carried out by taking that

• (a) the failure and repair rates of the crystallization subsystem (β ₁, µ ₁) and its standby unit (β ₂, µ ₂) are the same;

• (b) the failure and repair rates of the centrifugal pump subsystem (β ₃, µ ₃) and its standby units (β ₄, µ ₄ and β ₅, µ ₅) are the same.

The fuzzy availability of the crystallization system is computed for 1 year (i.e., time, t = 60–360 days). The different choices of failure rate and repair rate of the subsystems at different values of coverage factor (c) are computed to observe their effect on the fuzzy availability of the system. The data regarding the failure and repair rates of all the subsystems are taken from the plant personnel as stated earlier in Sect. 2. The fuzzy availability of the system (A _F) is composed of fuzzy availability of the system working with full capacity and its standby states, i.e.,

$$ A_{\text{F}} \; = \;P_{ 1} \; + \;\frac{ 1}{ 2}\,P_{ 2} \; + \;\frac{ 1}{ 2}\,P_{ 3} \; + \;\frac{ 1}{ 4}\,P_{ 4} \; + \;\frac{ 1}{ 2}\,P_{ 5} \; + \;\frac{ 1}{ 4}\,P_{ 6} . $$

(19)

Performance analysis of the system

In this section, the fuzzy availability of the system is computed using Eq. (19), and the effect of change in the failure and repair rates of subsystems and coverage factor (c) on the fuzzy availability of the system is presented in Tables 1, 2 and 3.

Table 1 Effect of failure and repair rates of the crystallization subsystem on the fuzzy availability of the system

Table 2 Effect of failure and repair rates of the centrifugal pump subsystem on the fuzzy availability of the system

Table 3 Effect of failure and repair rates of the sugar grader subsystem on the fuzzy availability of the system

Effect of failure and repair rates of the crystallization subsystem on the fuzzy availability of the system

The effect of the failure rate of the crystallization subsystem on the fuzzy availability of the system is studied by varying their values as: β ₁ = 0.0011, 0.0012, 0.0013 and 0.0014 at the repair rate (µ ₁) 0.023 at different values of the coverage factor. The failure and repair rates of other subsystems were taken as: β ₃ = 0.0025, β ₆ = 0.008, β ₂ = β ₁, β ₃ = β ₄ = β ₅, µ ₃ = 0.042, µ ₆ = 0.014, µ ₂ = µ ₁, µ ₃ = µ ₄ = µ ₅. The fuzzy availability of the system is calculated using this data and the results are shown in Table 1 and presented in Fig. 3. This table shows that the fuzzy availability of the system decreases from 22.782 to 1.75 % approximately with the increase of time. However, it decreases by 0.6 % approximately with the increase in the failure rate of the crystallization subsystem approximately. Figure 3 shows that the rate of change in the fuzzy availability of the system increases with the increase in the value of the system coverage factor (as 0 ≤ c ≤ 1) and decreases with time.

Fig. 3

Effect of variation in the failure rate of crystallization subsystems on the fuzzy availability of the system

The effect of the repair rate of the crystallization system on the fuzzy availability of the system is studied by varying their values as: µ ₁ = 0.018, 0.023, 0.028 and 0.033 at a failure rate of (β ₁) 0.0012. The failure and repair rates of other subsystems have been taken as: β ₃ = 0.0025, β ₆ = 0.008, β ₂ = β ₁, β ₃ = β ₄ = β ₅, µ ₃ = 0.042, µ ₆ = 0.014, µ ₂ = µ ₁ and µ ₃ = µ ₄ = µ ₅. The fuzzy availability of the system is calculated using this data and the results are shown in Table 1 and presented in Fig. 6. This table shows that the fuzzy availability of the system decreases from 1.523 to 22.782 % approximately with the increase of time. However, it increases by 1.412 % approximately with the increase in the repair rate of the crystallization system approximately. Figure 6 shows that the rate of change in fuzzy availability of the system decreases with the increase in the value of the system coverage factor (as 0 ≤ c ≤ 1) and decreases with time.

The effect of failure and repair rates of the centrifugal pump subsystem on the fuzzy availability of the system

The effect of the failure rate of the centrifugal pump subsystem on the fuzzy availability of the system is studied by varying their values as β ₃ = 0.0024, 0.0025, 0.0026 and 0.0027 at repair rate (µ ₃) 0.042 at different values of the coverage factor. The failure and repair rates of the other subsystems have been taken as β ₁ = 0.0012, β ₆ = 0.008, β ₂ = β ₁, β ₃ = β ₄ = β ₅, µ ₆ = 0.014, µ ₂ = µ ₁ and µ ₃ = µ ₄ = µ ₅. The fuzzy availability of the system is calculated using this data and the results are shown in Table 2 and Fig. 4. This table shows that the fuzzy availability of the system decreases from 22.782 to 2.0 % approximately with the increase of time. However, it decreases by 0.364 % approximately with the increase in the failure rate of the centrifugal subsystem approximately. Figure 4 shows that the rate of change in the fuzzy availability of the system increases with the increase in the value of the system coverage factor (as 0 ≤ c ≤ 1) and decreases with time.

Fig. 4

Effect of variation in the failure rate of the centrifugal pump subsystem on the fuzzy availability of the system

The effect of repair rate of the centrifugal system on the fuzzy availability of the system is studied by varying their values as µ ₃ = 0.037, 0.042, 0.047 and 0.52 at a failure rate of (β ₃) 0.0025. The failure and repair rates of other subsystems have been taken as β ₁ = 0.0012, β ₆ = 0.008, β ₂ = β ₁, β ₃ = β ₄ = β ₅, µ ₁ = 0.023, µ ₆ = 0.014, µ ₂ = µ ₁ and µ ₃ = µ ₄ = µ ₅. The fuzzy availability of the system is calculated using this data and the results are shown in Table 2 and Fig. 7. This table shows that the fuzzy availability of the system decreases from 1.748 to 22.782 % approximately with the increase of time. However, it increases by 0.364 % approximately with the increase in the repair rate of the centrifugal subsystem approximately. Figure 7 shows that the rate of change in fuzzy availability of the system decreases with the increase in the value of the system coverage factor (as 0 ≤ c ≤ 1) and decreases with time.

Effect of failure and repair rates of the sugar grader subsystem on the fuzzy availability of the system

The effect of the failure rate of the sugar grader subsystem on the fuzzy availability of the system is studied by varying their values as β ₆ = 0.007, 0.008, 0.009 and 0.01 at a repair rate (µ ₆) 0.014 at different values of the coverage factor. The failure and repair rates of other subsystems have been taken as β ₁ = 0.0012, β ₃ = 0.0025, β ₂ = β ₁, β ₃ = β ₄ = β ₅, µ ₂ = µ ₁ = 0.023 and µ ₃ = µ ₄ = µ ₅ = 0.042. The fuzzy availability of the system is calculated using this data and the results are shown in Table 3 and Fig. 5. This table shows that the fuzzy availability of the system decreases from 25.786 to 2.0 % approximately with the increase of time. However, it decreases by 6.878 to 12.512 % approximately with the increase in failure rate of the sugar grader subsystem approximately. Figure 5 shows that the rate of change in fuzzy availability of the system increases with the increase in the value of the system coverage factor (as 0 ≤ c ≤ 1) and decreases with time.

Fig. 5

Effect of variation in the failure rate of the sugar grader subsystem on the fuzzy availability of the system

The effect of the repair rate of the sugar grader system on the fuzzy availability of the system is studied by varying their values as µ ₆ = 0.009, 0.014, 0.019 and 0.024 at a failure rate of (β ₆) 0.008. The failure and repair rates of other subsystems have been taken as β ₁ = 0.0012, β ₂ = β ₁, β ₃ = β ₄ = β ₅ = 0.025, µ ₁ = 0.023, µ ₂ = µ ₁ and µ ₃ = µ ₄ = µ ₅ = 0.042. The fuzzy availability of the system is calculated using this data and the results are shown in Table 3 and Fig. 8. This table shows that the fuzzy availability of the system decreases from 2.1 to 34.672 % approximately with the increase of time. However, it increases by 12.664 % approximately with the increase in the repair rate of the sugar grader subsystem approximately. Figure 8 shows that the rate of change in the fuzzy availability of the system decreases with the increase in the value of the system coverage factor (as 0 ≤ c ≤ 1) and decreases with time.

Conclusion

Analysis of fuzzy availability of crystallization system helps in increasing the production of sugar. The effects of coverage factor (c) corresponding to different values of failure and repair rates of all the subsystems are presented in Tables 1, 2 and 3 and shown graphically in Figs. 3, 4, 5, 6, 7 and 8. A comparative study concludes that the sugar grader subsystem has a prominent effect on the fuzzy availability of the system than that of other subsystems. The numeric results show that all the fuzziness, system coverage factor and maintenance have a significant effect on the fuzzy availability of the crystallization system. These results are presented and discussed with the plant personnel to adopt and practice suitable maintenance policies/strategies to enhance the performance of the crystallization system of the sugar plant.

Fig. 6

Effect of variation in the repair rate of the crystallization subsystem on the fuzzy availability of the system

Fig. 7

Effect of variation in the repair rate of the centrifugal pump subsystem on the fuzzy availability of the system

Fig. 8

Effect of variation in the repair rate of the sugar grader subsystem on the fuzzy availability of the system