Introduction

From 1991 till now, Carbon nanotubes (CNTs), discovered by Sumio Ijima, have huge amount of scientific research from numerous fields (i.e.; material science, mechanical science, chemistry, and physics sciences) and real applications (i.e.; nano-electronics, nano-switch, solar cell, medical tools, and nano-devices). CNT is the strongest material known until now, with astonishing mechanical properties (Eltaher et al. 2016).

To comprehend mechanical behaviors of CNTs, the experimental and theoretical studies (i.e.; atomistic modeling, molecular simulation, and advanced continuum mechanics) are exploited. Krishnan et al. (1998) assessed the modulus of elasticity of SWCNTs using TEM. Salvetat et al. (1999) exploited AFM to evaluate shear and elastic moduli of SWNT ropes, which are in the order of 1 GPa and 1 TPa, respectively. They found that low inter-tube shear effect controls the flexural deformation of SWNTs. Charlier (2002) investigated, theoretically, the effects of different types of imperfections, such as vacancies, or dopant on the electronic properties of CNTs. He concluded that vacancies drastically modify the electronic behaviors and characteristics of those nano-systems. Mielke et al. (2004) exploited the quantum mechanical theory and Tersoff–Brenner potential of molecular mechanics (MM) to explore the effects of vacancies and holes defects in the fracture of SWCNTs. Ma et al. (2004) studied magnetic behaviors of vacancies in graphene and SWCNTs using spin-polarized density functional theory.

Wang and Varadan (2006) investigated the wave characteristics in CNTs, which was proposed from the discrete atomic nature, via beam theories. They recommended the Timoshenko beam model to analyze a wave transition in SWCNTs in case of terahertz frequency range. Soltani et al. (2012) considered transverse vibrations of light axial waviness of SWCNT. They considered tube as a thin and thick beam, and so, they modeled it by Euler–Bernoulli and Timoshenko theories. Gajbhiye and Singh (2015) proposed different techniques including a potential of Tersoff–Brenner to study the vibration behaviors of open-end and capped-end of SWCNTs. They concluded that zigzag and armchair structures display akin vibration features at lower vibration modes, and different dynamical features at very high resonant frequencies. Zemri et al. (2015) exploited nonlocal Eringen and higher order shear beam theory to study the mechanical behaviors of FG nanobeams. Chaht et al. (2015) addressed static bending and static stability buckling behaviors of nonlocal FG nano-scale beams considering the effect of thickness stretching. Belkorissat et al. (2015) developed a new hyperbolic plate theory to study the vibrations of FG nonlocal Nano-scale plate. Eltaher and Agwa (2016) studied theoretically the vibration behaviors of SWCNTs carrying a concentrated mass under pretension. The study presented that the SWCNT resonator can sense a very minute mass weighting 10−1 zeptogram. Eltaher et al. (2016) examined material and size dependencies’ effects on nonlinear bending behavior of CNTs by energy-equivalent model. Ahouel et al. (2016) exploited both nonlocal Eringen and trigonometric shear theory to study mechanical behaviors of FG nonlocal Eringen nanobeams as well as neutral axis effects. Tahouneh et al. (2016) investigated the material properties of nanocomposites reinforced by CNT arrays using the representative volume element (RVE). Agwa and Eltaher (2016) developed the modified continuum approach to examine the impacts of surface energy and surface tension on flexural vibrations frequencies of nano-mass sensor using carbyne materials. Bellifa et al. (2017) suggested zero shear theory to investigate the nonlinear postbuckling of nano-scale Eringen beams considered the axial displacement. Bouafia et al. (2017) examined the size and stretching effects on static transverse bending and flexural vibration of FG nonlocal nano-scale beams implemented by the quasi-3D shear theory. Bounouara et al. (2016), Khetir et al. (2017), and Besseghier et al. (2017) employed zero shear and refined trigonometric shear theories to analyze buckling and vibration of FG nonlocal Eringen nano-plates attached with an elastic media. Mouffoki et al. (2017) presented the vibration behaviors of nonlocal hygro-thermal nanobeams modeled by two-unknown trigonometric shear deformation beam theory. Karami et al. (2017) studied tri-axial magnetic effects on wave propagations of anisotropic nonlocal-strain-gradient nano-plates.

Yazid et al. (2018) exploited two-variable refined plate to investigate static buckling of graphene orthotropic nano-plates rested on elastic medium. Eltaher et al. (2018a, b) exploited energy-equivalent model and modified coupled stress to discover vibrational characteristics of SWCNTs modeled as a beam structure. The impact of size-parameter, chiral vector translation indices, and orientation on the vibration behaviors are illustrated. Mokhtar et al. (2018) and Kadari et al. (2018) analyzed the buckling behavior of graphene sheet modeled by nonlocal Eringen differential form and simple shear plate theory. Bouadi et al. (2018) investigated critical buckling forces of graphene sheets that modeled by nonlocal higher order shear deformation theory. Esbati and Irani (2018) exploited stochastic finite-element methods to evaluate structural reliability and probabilistic fracture properties of CNTs. Hamza-Cherif et al. (2018) illustrated thermal effects on vibration of SWCNT nanobeam surrounded by an elastic foundation. Shahabodini et al. (2018) developed a numerical multiscale analysis to study the vibrations of SWCNTs modeling its kinematics membrane by Cauchy–Born rule. Bianco et al. (2018) developed the complete formulation of linear stiffness matrices, which is practiced in beam theory under constant and/or linear loading distribution in the longitudinal direction. Karami et al. (2018a, b) exploited a nonlocal-strain-gradient on higher order shell structural model to predict the mechanical characteristics and waves of anisotropic nano-shells. Vila et al. (2018) deliberated the effects of axial and transverse coupling on nonlinear vibrations of one-dimensional solid structures using inertia gradient continuum model. Ahmadabadi et al. (2018) illustrated the thermal dependence of zigzag SWCNT diameter on the state of its density. Bakhadda et al. (2018) analytically examined bending and vibration response of four types of distributions of uniaxial-aligned CNT-reinforced plates rested on the Pasternak foundation by hyperbolic shear theory. Eltaher et al. (2019) exploited equivalent-continuum mechanics approach and finite-element method to characterize the mechanical behaviors of SWCNTs. Eltaher et al. (2019) studied the nonlinear postbuckling behaviors of curved carbon nanotubes using energy-equivalent model and Euler–Bernoulli beam kinematic relations.

Nevertheless, CNTs are, perhaps, not like completely perfect structures as they are once supposed to be. Imperfections like vacancies and/or dopant extremely change the mechanical, electrical, and chemical properties of CNTs. Most of the previous studies considered the defects effect using only molecular simulations. The current paper propose a modified continuum mechanics model with finite-element simulation to present the effects of vacancies on the vibration behaviors and modal participation factors of fixed–fixed SWNCT. Sound effects of vacancy on deactivation and activation of mode shapes are presented for the first time for fixed–fixed-supported CNT structures. Coupled modes and uncoupled modes are also investigated and presented. The atomic bond between adjacent atoms is modeled as beam element. The energy-equivalent model is recommended to extract the equivalent mechanical energy of the structure with that in the chemical bond between atoms. Nanotube modeler is exploited to create a geometrical structure of CNTs to be impeded into the finite-element model to extract the modal participation factors and the vibration behaviors of these structures. Different orientation of CNTs, such as armchair and zigzag, are studied. Effect of tube length is also presented.

Geometrical structural of SWCNTs

Carbon nanotube, which is layer of graphene sheet wrapped into cylindrical shape with a diameter about 1 nm and a length up to many micrometers, is controlled by chiral angle orientation and tube diameter. The vector used to depict a chiral angle is as follows:

$$\vec{C}_{h} = n\vec{a}_{1} + m \vec{a}_{2} ,$$
(1)

in which \(\vec{a}_{1}\) and \(\vec{a}_{2}\) are basis vectors. An integer pair \((n, m)\) is used to specify structure orientation of CNTs, as presented in Fig. 1. The lattice basis vectors in Cartesian coordinates can be portrayed by the following:

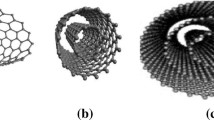
$$\vec{a}_{1} = \left( {\frac{{\sqrt {3a} }}{2}, \frac{a}{2}a} \right),\quad \vec{a}_{2} = \left( {\frac{{\sqrt {3a} }}{2}, - \frac{a}{2}} \right),$$
(2)

where \(a = \sqrt 3 a_{{{\text{c}} - {\text{c}}}} ,\) is the lattice constant, and \(a_{{{\text{c}} - {\text{c}}}} = 1.42\) Å is the bond length. In case of n = m, the nanotube is called armchair structure. If m is equal to zero, SWCNT is called a zigzag structure. Elsewhere, the nanotube is donated as chiral structure. Figure 2 shows three possible orientations of CNTs structure. Figure 2a represents the orientation of graphene sheets before rolling, whereas Fig. 2b shows the structure of grapheme sheet after rolling to NTs.

Fig. 1
figure 1

Hexagonal lattice of graphene sheet and its orientations and basis vectors

Full size image
Fig. 2
figure 2

Three possible structure orientation of SWCNTs

Full size image

The relationships among nanotube diameter \((d_{\text{nt}} )\) and lattice vectors basis can be represented by the following:

$$d_{\text{nt}} = a\sqrt {n^{2} + m^{2} + nm} .$$
(3)

The relationships between chiral angle \((\theta_{\text{ch}} )\) and lattice vectors basis can be described as follows:

$$\theta_{\text{ch}} = \cos^{ - 1} \left( {\frac{2n + m}{{2\sqrt {n^{2} + m^{2} + nm} }}} \right).$$
(4)

In case of zigzag and armchair orientations, the diameter of nanotube can be calculated by \(d_{t} = \frac{\sqrt 3 na}{\pi }\), and \(d_{t} = \frac{3na}{\pi }\), respectively. Note the chiral angle in zigzag = 0, while the chiral angle in the armchair = 30. This is the maximum angle, after which the NT structure begins to repeat its orientation.

Chemical energies vs mechanical energies

To get a relationship between microscopic chemical energies of CNTs and their corresponding macroscopic mechanical energies, covalent bonding among carbon’s atoms is represented by a force filed. The force filed is represented by a potential energy of chemical bond \(U_{\text{ch}}\) as follows (Rappé et al. 1992):

$$U_{\text{ch}} = U_{L} + U_{\theta } + U_{T} + U_{\omega } ,$$
(5)

where \(U_{L}\) is bond-stretching energy, \(U_{\theta }\) is angle variation energy, \(U_{T}\) is torsion energy, and \(U_{\omega }\) is inversion energy.

When SWCNTs exposed to tension loads and transverse bending load in the 2D plane analysis, the most substantial energies included are bond-stretching and angle energies, and others can be neglected. Consequently, Eq. (5) can be reduced to the following (Wu et al. 2006; Shokrieh and Rafiee 2010; Eltaher et al. 2019):

$$U_{\text{ch}} = U_{L} + U_{\theta } = \frac{1}{2}\mathop \sum \limits_{i} K_{i} ({\text{d}}R_{i} )^{2} + \frac{1}{2}\mathop \sum \limits_{j} C_{i} ({\text{d}}\theta_{i} )^{2} ,$$
(6)

where \(K_{i}\) is the stretching spring parameter, \({\text{d}}R_{i}\) is the element of stretching, \(C_{i}\) is the rotational spring parameter, \({\text{d}}\theta_{i}\) is the element of rotation angle, and \(i\) is corresponding to the bond number.

By assuming that, the chemical covalent bond can be represented by beam structure, and based on continuum mechanics, the total energy stored in beam element can be composed mainly from tension and bending deformations. Hence, the total mechanical energy of a beam is depicted by the following:

$$U_{m} = U_{T} + U_{b} = \frac{1}{2}\frac{EA}{L}(\Delta L)^{2} + \frac{1}{2}\frac{EI}{L}(2\alpha )^{2} ,$$
(7)

where \(E\) corresponds to Young’s modulus, \(L\) is the beam length, \(A\) is the beam cross-sectional area, \(I\) is the beam area moment, \(\Delta L\) is the stretching length, and \(2\alpha\) is the rotation angle due to bending moment. By equating chemical energy in single atom–atom bond described in Eq. (6) with Eq. (7) of total energy of the beam, it can be concluded that:

$$K_{i} = \frac{EA}{L}\quad {\text{and}}\quad C_{i} = \frac{EI}{L}.$$
(8)

Since the bond is circular cross-sectional, the geometrical parameters of the bond can be calculated by the following:

$$A = \frac{{\pi d^{2} }}{4}\quad {\text{and}}\quad I = \frac{{\pi d^{4} }}{64}.$$
(9)

Substitute Eq. (9) into Eq. (8), the bonding diameter (\(d\)) and \(E\) modulus of equivalent beam element are as follows:

$$d = 4\sqrt {\frac{{C_{i} }}{{K_{i} }}} \quad {\text{and}}\quad E = \frac{{(K_{i} )^{2} }}{{4\pi C_{i} }}.$$
(10)

Dimension modification

In general, finite-element analysis of beam structure is insensitive to geometrical scale of nanometer in its analysis. Therefore, some adaptations from nano-scale to macro-scale units must be prepared before entering the input data into the finite-element model. Therefore, the following transformations have been implemented (Table 1).

Table 1 Modified dimensions for the finite-element model software
Full size table

Numerical results

Validation

First, the main core of this section is to confirm that the methodology of the present study is on the right track. The methodology in Gajbhiye and Singh (2015) represents carbon nanotubes as beam element and mass element using the ANSYS program. The same methodology is used in the current work without using mass elements. Fixed–fixed boundary conditions for CNT (5, 5) are proposed. The material properties of CNTs are Young’s modulus E = 21.607 × 1012 Pa, Poisson ratio υ = 0.28, and density = 1.9 kg/m3. The geometric properties are: L = 69.29 Å, d = 0.716 Å, t = 3.4 Å, and ac–c = 0.145 nm = 1.45 Å. as represented by Gajbhiye and Singh (2015).

The first seven fundamental frequencies of armchair nanotube (5, 5) are demonstrated in Table 2. As observed, the current results do not agree with that obtained by Gajbhiye and Singh (2015) with a maximum difference of 12.5% at fifth mode. This difference occurs, because the current model uses 3D beam element with uniformly distributed mass; however, Gajbhiye and Singh (2015) assumed the CNT as elastic beam with lumped carbon masses at tits two ends.

Table 2 First seven frequency values f (THZ) for capped CNT (5, 5) with CNT length L = 69.29 Å
Full size table

Effect of defect position of SWCNT

This section is devoted to illustrating the effect of defect position on fundamental frequencies and modal participation factor in case of zigzag and armchair orientations. Two defected positions are proposed, which are at one of the fixed ends titled with side defect and at the middle of the tube titled with middle defect, as shown in Fig. 3. A zigzag (10, 0) and armchair (10, 10) orientations are supported from both sides for fixed–fixed configuration. Figure 3 illustrates the prefect and imperfect (defected) configurations of CNT in case of zigzag and armchair orientations.

Fig. 3
figure 3

Perfect, side defect, and middle defect (vacancy) of SWCNT with 50 Å length

Full size image

3D beam element is exploited to describe and simulate the C–C bond, with the following geometrical properties d = 0.716 Å, t = 3.4 Å, ac–c = 0.145 nm = 1.45 Å, and 0.34 nm wall thickness, (Rappé et al. 1992) and the following material properties: E = 5.49E12 Pa, υ = 0.3, and density = 1.7 kg/m3. The overall length of SWCNT is 50 Å.

  1. (a)

    Zigzag-capped SWCNT (10, 0)

Table 3 illustrates the effect of defect location on the first ten natural frequencies and the modal participation factors for Zigzag (10, 0) SWCNTs. It is worth noting that the first and second natural frequencies are equal in their values, but have different modal participation in case of prefect tube (un-defected). The defected conditions show significant changes in the first and second frequencies and their values become unequal. The modal participation is affected in case of side defect; however, the middle defect has no effect on the first two mode shapes. The third frequency increases from 610.80 to 647.22 GHz as defect occurs in the middle and decreases to 606.38 in case of side defect. However, their modal participation is not affected by the defect. As shown in Table 3, the middle defect is more significant on the fundamental frequencies than the side defect, which has the same value of natural frequencies at higher level with perfect tube.

Table 3 The first ten frequency values f (GHz) for zigzag CNT (10, 0) with CNT length L = 50 Å
Full size table

The modal participation factor for the perfect and the two defected tubes are shown in Fig. 4. In case of free defect zigzag SWCNTs, the modal participation with displacement in X-DIR (UX) is dominant in both second and third modes. The modal participation with displacement in Y-DIR (UY) is dominant in both first and seventh modes. However, the modal participation with displacement in Z-DIR (UZ) is mostly dominant in sixth mode. The modal participation with rotational around x-axis (RX), y-axis (RY), and z-axis (RZ) are dominant in the first, second, and third modes, respectively.

Fig. 4
figure 4

Modal participation factor for zigzag (10, 0) CNT without defect (length = 50 Å)

Full size image

The modal participation factors in cases of middle defect are the same as in case of non-defected cases, except in the RZ direction. The modal participation with rotational in RZ direction changes from third mode in case of non-defected tube to the third and fourth modes in case of middle defected tube, as shown in Fig. 5. The side defect tends to change the modal participation of first mode from UY&RX (as in the other cases of non-defected and defected with middle defect) to UX&RY. In addition, the side defect tends to change modal participation of second mode from UX&RY to UY&RX, as presented in Fig. 6.

Fig. 5
figure 5

Modal participation factor for zigzag (10, 0) CNT with middle defect (length = 50 Å)

Full size image
Fig. 6
figure 6

Modal participation factor for zigzag (10, 0) CNT with side defect (length = 50 Å)

Full size image
  1. (b)

    Armchair CNT (10, 10)

Table 4 illustrates the effect of defect location on the first ten natural frequencies and the modal participation factors for Armchair (10, 10) SWCNTs. It is worth noting that the first and second natural frequencies are equal in their values, but have different modal participation in case of prefect tube (non-defected). The defected conditions show significant changes in the first and second frequencies and their values become unequal. The modal participation is affected in case of side defect; however, the lower defect has no effect on the modal participation of the first two mode shapes.

Table 4 First ten frequency values f (GHz) for armchair CNT (10, 10) with CNT length L = 50 Å
Full size table

The third and fourth mode shapes do not have modal participation at any direction, which are kept with the same behavior with the middle defect. As shown in Table 4, the middle defect is more significant on the modal participation more than the side defect.

The modal participation factor for the perfect and the two defected tubes are shown in Figs. 7, 8, and 9. In case of non-defected Armchair SWCNTs, the modal participation with displacement in X-DIR (UX) is dominant in the first mode. The modal participation with displacement in Y-DIR (UY) is dominant in the second mode. In addition, no participation is observed with displacement in Z-direction. The modal participation with rotational around Y-axis (RY), x-axis (RX), and z-axis (RZ) are dominant in first, second, and fifth mode, respectively. All other modes have neither significant displacement nor rotational modal participations.

Fig. 7
figure 7

Modal participation factor for armchair (10, 10) CNT without defect (length = 50 Å)

Full size image
Fig. 8
figure 8

Modal Participation factor for armchair (10, 10) CNT with middle defect (length = 50 Å)

Full size image
Fig. 9
figure 9

Modal participation factor for armchair (10, 10) CNT with lower defect (length = 50 Å)

Full size image

The modal participation factors in cases of side defect are the same as in case of non-defected cases, except at the eighth and ninth modes, the side defect created rotational modal participation about Y-axis and X-axis, respectively. The middle defect has changed the modal participation for all modes except the fifth mode, which is kept with rotational modal participation around Z-direction.

Length effects on the defected SWCNT at the middle position

As concluded from the previous results, the most significant position of the defect is at the middle of the tube, middle defect. Therefore, the effect of SWCNT length on the modal participation factors and natural frequencies are studied in this section for middle defected tubes. Both Zigzag (10, 0) and Armchair (10, 10) with different tube lengths, 50 Å, 100 Å, 150 Å, and 180 Å are studied.

The effect of tube length on natural frequencies of Zigzag (10, 0) and Armchair (10,10) SWCNT’s are presented in Tables 5 and 6, respectively. As concluded, by increasing the NTs lengths, the natural frequencies decrease for defected and non-defected tubes. In addition, the middle defect tends to reduce the stiffness at the modes with bending modal participations in tubes longer than 100 Å. Short tubes with bending modal participation around X-direction and with translational modal participation in Y-direction shows lower natural frequencies due to middle defects. The defect has less significant effects on the long tubes due to the dominating of the length weakness than the defect weakness. First and second modes of the non-defected tube have similar natural frequencies, and the third and fourth modes have similar natural frequencies as well. The middle defect changes the modal participation of these modes with less significant changes to the natural frequencies for the long tubes.

Table 5 First tenth frequencies (GHz) and active modes for zigzag CNT (10, 0) without and with middle defect at different lengths
Full size table
Table 6 First tenth frequencies (GHZ) and active modes for armchair CNT (10, 10) without and with middle defects at different lengths
Full size table

Conclusion

In this article, a continuum mechanics that is derived from the basis molecular simulation is adopted to investigate vibrational behaviors of fixed–fixed SWCNTs with vacancy defects at different lengths. A numerical finite-element analysis with the nanotube software modeler is exploited to study the problem. Effects of vacancy position and tube length on the natural frequencies, mode shapes, and modal participation factors are presented for both fixed–fixed-supported zigzag and armchair orientations. Conclusions from this study can be summarized as follows:

  1. 1.

    The defects tend to decrease the natural frequencies of short tubes either zigzag or armchair SWCNTs if the defect is in the middle or at near to the fixed edge. In this case, the reduction in overall stiffness is more than the reduction in overall mass of SWCNT.

  2. 2.

    The defect tends to increase the natural frequencies, if its position is not affecting the modal participation, I which, the reduction in overall mass is higher than the reduction in stiffness.

  3. 3.

    Twelve modes are satisfied to describe accurately the vibrational behaviors of zigzag (10, 0) SWCNTs. However, 20 modes should be developed in case of armchair (10, 10) to study its vibrational behaviors.

  4. 4.

    Increasing of SWCNT length tends to decrease the natural frequencies of perfect CNTs.

  5. 5.

    The tube length and defects may activate and deactivate mode shapes.

  6. 6.

    Mode shapes in X-DIR and Y-DIR are significant in lower frequencies. However, modes in Z-DIR are more pronounced at higher vibrational frequencies.