Introduction

It has recently been shown that the concepts underlying code specifications for the design of reinforced concrete structures (RC) is incompatible with fundamental concrete properties such as post-peak stress–strain characteristics, mechanism of crack extension, and sensitivity of strength and deformation characteristics to the presence of small confinement stresses (acting orthogonal to the direction considered) (Kotsovos 2015). Consequently, the need of calibrating these specifications with experimental data describing the behaviour of RC beam/column elements leads to an ever increasing complexity of the code-adopted design formulae. Moreover, it has been shown that compliance with the fundamental concrete properties can lead to the development of alternative design methods, such as the compressive force path (CFP) method, which may be, not only simpler and more efficient, but also rely on failure criteria derived from first principles (of mechanics), without the need of calibration through the use of experimental data (Kotsovos 2014).

To this end, the present work has been aimed at evaluating the shear design specifications of some of the most widely adopted codes of practice (ACI 445R-99 1999, ACI 318 2014, Eurocode 2 2004, JSCE 2007, CSA 2007, NZ 2006) and the CFP method (Kotsovos 2014) as regards, not only the closeness of the correlation of the calculated values of load-carrying capacity with their experimentally established counterparts, but also the validity of the concepts underlying the development of the method of calculation. The present study focuses on comparing the values of load-carrying capacity predicted by the design codes with those obtained through the use of a purely empirical (soft computing) method that employs artificial neural networks (ANNs) (Cladera and Mari 2004a, b; Mansour et al. 2004; Abdalla et al. 2007; Yang et al. 2007; Jung and Kim 2008) capable of providing predictions concerning load-carrying capacity that correlate closely to the available test data. In what follows the description of the ANN approach developed herein and the presentation and discussion of the results of the comparative study are preceded by a concise description of the methods of calculation employed and the presentation of the experimental information used for the training and verification of the ANNs.

Experimental information on RC structural response at ULS

To date, a large number of experiments have been conducted on simply supported RC beam specimens to study the mechanics underlying RC structural response throughout the loading process and establish the effect of a wide range of parameters [e.g., width (b), effective depth (d), shear span-to-depth ratio (αv/d), compressive strength of concrete (fc), longitudinal (ρl) and transverse (ρw) steel reinforcement ratios, yield strength of longitudinal (fyl) and transverse (fyw) reinforcement bars, etc.] on the exhibited behaviour (Κani 1964; Panagiotakos and Fardis 2001; Reineck 2013; Reineck et al. 2014; Kotsovos 2014). During testing, attention is focused on measuring certain aspects of the exhibited behaviour such as the applied load and reaction forces, the displacement of certain points along the element span as well as the strain at specific critical locations (i.e., the compressive region or on the steel longitudinal and transverse reinforcement bars). In addition, the deformation profiles and crack patterns forming as well as the exhibited mode of failure are also recorded, as they provide important information concerning the internal stress state developing within the members considered. The test data published and the different parameters considered have been used to form an extensive database describing the effect of the above parameters on the exhibited behaviour mainly at ULS (see Tables A1 and A2 presented as supplementary material).

Design methods

Current design methods are intended to size the cross section of structural members and specify an amount and arrangement of reinforcement that will safeguard desired performance characteristics such as load-carrying capacity and ductility. This objective can only be achieved by ensuring that the load corresponding to shear types of failure is always higher than that corresponding to flexural capacity. To this end, the sizing of the cross section and the assessment of the longitudinal reinforcement are linked to flexural capacity, whereas the associated shear-force diagram underlies the method adopted for specifying an amount and arrangement of transverse reinforcement that will safeguard against shear failure occurring before flexural capacity is exhausted.

Code-adopted methods

The concepts underlying the methods adopted by the majority of the available RC design codes assume that load transfer at ULS is accomplished through the development of truss or various forms of strut-and-tie mechanisms (a simplified form of which is depicted in Fig. 1) in which the compressive zone and the tension flexural reinforcement form the longitudinal struts and ties, respectively, stirrups and inclined bars form the web ties and cracked concrete in the tensile zone (by means of aggregate interlock and dowel action) allows for the formation of inclined struts. On the basis of these concepts, shear failure is associated with failure of either the web ties or the inclined struts, whereas the longitudinal struts and ties are designed such that flexural failure occurs when the concrete strut at the most critical location reaches its strength (in compression) after yielding of the longitudinal tie at the same cross section. To determine shear capacity each code employs its own empirical formulae (see Table 1), the derivation of which is largely based on regression analysis of the available test data, whereas the calculation of flexural capacity is based on assumptions such as plane cross sections remain plane during bending, full bond between concrete and steel, uniaxial stress–stain behaviour of concrete in the compressive zone, etc.

Fig. 1
figure 1

Code design methods: a truss model of a beam-like RC element; b portion of truss in Fig. 1 between cuts 1–1 and 2–2 indicating the mechanism of load transfer

Full size image
Table 1 Formulae adopted by the RC design codes for predicting shear capacity
Full size table

The CFP method

The CFP method is based on the incorporation of important mechanical characteristics of concrete such as brittle behaviour, cracking mechanism, sensitivity to triaxial stress conditions, etc. into beam theory which describes the mechanism of load transfer accomplished through the bending of the concrete cantilevers forming between consecutive flexural and/or inclined cracks (see Fig. 2). Failure is considered to be associated with the stress conditions in the compressive zone and reinforcement is specified to prevent non-flexural (commonly referred to as shear) types of failure before flexural capacity is exhausted. Unlike the code methods, the criteria for non-flexural types of failure have been derived from first principles without the need of calibration through the use of test data. The method is fully described elsewhere (Kotsovos 2014) and, therefore, is only briefly presented in what follows.

Fig. 2
figure 2

CFP method: a schematic representation of the physical state of an RC beam at the ULS; b mechanism of load transfer

Full size image

The CFP theory attributes what is commonly referred to as ‘shear’ failure to the development of tensile stresses at particular locations [dependent on the shear span-to-depth ratio (av/d)] along the compressive zone. For an RC beam/column element with flexural reinforcement only, the values of the shear force corresponding to such types of failure are obtained from.

For av/d > 2.5, failure occurs when either the shear force at a distance equal to 2.5d from a simple support or a point of contra-flexure attains a critical value:

$$V_{\text{II,1}} = 0. 5f_{\text{t}} bd,$$
(1)

where ft is the tensile strength of concrete and b, d are the width and depth of the cross section, or after yielding of the flexural reinforcement in regions, where the value of the shear force attains a critical value:

$$V_{\text{II,2}} = F_{\text{c}} [ 1- 1/( 1+ 5 |f_{\text{t}} |/f_{\text{c}} )],$$
(2)

where Fc is the value of the compressive force developing on account of bending when Mf is attained and fc and ft are the values of the compressive and tensile, respectively, strengths of concrete.

For 1 ≤ av/d ≤ 2.5, failure is considered to occur when the bending moment at the cross section located at a distance equal to av from the closest simple support or point of contra-flexure exceeds a critical value:

$$M_{\text{III}} = M_{\text{II}} + (M_{\text{f}} - M_{\text{II}} )( 2. 5- a_{\text{v}} )/( 1. 5d),$$
(3)

obtained by linear interpolation between the values MII = VII (2.5d) and MIV = Mf (flexural capacity) at cross sections at distances of 2.5d and d, respectively, from the closest simple support or point of contra-flexure.

For av/d < 1, failure occurs when the shear force exceeds a critical value provided by Eq. (4):

$$V_{\text{IV}} = M_{\text{f}} /a_{\text{v}} .$$
(4)

When the above types of failure occur before flexural capacity is attained, they can be prevented by specifying transverse reinforcement in the form of stirrups in an amount sufficient to undertake the total tension developing at the locations indicated earlier as critical. More specifically, for av/d > 2.5, the transverse tension developing at a distance of 2.5d from the location of the simply support or the point of contra-flexure has been shown to be numerically equal to the shear force Vf developing at this location and, then, the amount of transverse reinforcement required to prevent failure is obtained from:

$$A_{\text{sv}} = V_{\text{f}} /f_{\text{yv}} .$$
(5)

Such reinforcement is spread over a length of 2d extending symmetrically on either side of the location, where transverse tension is considered to develop (i.e., the location at a distance from a simple support or a point of contra-flexure).

This method is also used to calculate the amount of transverse reinforcement required to prevent failure in the region of points of contra-flexure.

When Vf > VII,2 (where Vf is the shear force corresponding to Mf), the transverse tensile stresses σt exceed the tensile strength of concrete ft in the compressive zone of the regions of beam/column elements, where yielding of the flexural reinforcement occurs. Then, these tensile stresses can be calculated from Eq. (2) by replacing VII,2 with Vf and ft with σt, and solving for σt, that is

$$\left| {\sigma_{t} } \right| = f_{\text{c}} /[ 5(F_{\text{c}} /V_{\text{f}} - 1)],$$
(6)

and hence, the tensile force per unit length developing in this region is expressed by:

$$T_{\text{II,2}} = \sigma_{\text{t}} b/2.$$
(7)

The second term of Eq. (7) is divided by 2 to allow for the non-uniform distribution of the transverse stresses within the compressive zone.

Therefore, the amount of transverse reinforcement required per unit length to sustain TII,2 is equal to:

$$A_{\text{sv,II2}} = T_{\text{II,2}} /f_{\text{yv}} .$$
(8)

As regards the assessment of the transverse reinforcement to prevent failure for the case of 1 ≤ av/d ≤ 2.5, this is obtained from:

$$A_{\text{sv,III}} = 2(M_{\text{f}} - M_{\text{III}} )/(a_{\text{v}} f_{\text{yv}} ).$$
(9)

It should be noted that this reinforcement is uniformly distributed within the shear span and, in accordance with the CFP theory, is intended to increase flexural capacity from MIII to Mf rather than prevent shear failure.

It is also important to note that in accordance with the CFP theory, the specified transverse reinforce is effective when its spacing is smaller than d/2.

As regards the calculation of flexural capacity, this differs from the EC2 code method in that the normal stress distribution in the compressive zone is equivalent to a stress block covering the whole compressive zone; its intensity is obtained from:

$$\sigma_{\text{a}} = f_{\text{c}} + { 5}\left| {f_{\text{t}} } \right|.$$
(10)

The above expression has been derived by considering the triaxial stress conditions invariable developing in the compressive zone when ULS is approached.

Artificial neural networks

Artificial neural networks mimic their biological counterparts in the nervous system and the brains of animals and humans. They are used to estimate or approximate functions that depend on a large number of parameters, the effect of which is not clearly established or quantified. Due to their adaptive nature and ability to remember information introduced to them during training (calibration), ANNs can learn, generalize, categorize, and empirically predict values.

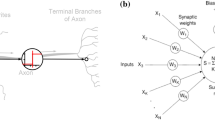
A typical artificial neuron (AN) designed to perform specific operations is schematically depicted in Fig. 3. From the figure, it can be seen that the AN is fed with the values of parameters xj (describing selected parameters associated with the design details and strength characteristics of the structural elements investigated), each of them being attributed an (initially assumed) weight wji and a bias Θi. This input information is used to form the sum ni of the products xj × wji and Θi, that is

$$n_{i} = \sum w_{ji} x_{j} + \varTheta_{i} .$$
(11)
Fig. 3
figure 3

Typical AN

Full size image

The sum ni is inserted as argument into an adopted activation function g, that is

$$y_{i} = g_{i} = g(\varSigma w_{ji} x_{j} + \varTheta_{\iota } ),$$
(12)

and the resulting value of g, yi = g(ni) is the output Oi of the AN.

ANs, such as that of Fig. 3, have been combined to form the artificial neural networks (ANNs) adopted for the present work, as depicted in Fig. 4. The process through which the ANNs have been developed is presented in a flowchart form in Fig. 5. The architecture of the ANNs models, which is associated with the selection of the type of activation function employed for each layer, the number of hidden layers and the number of neurons in each hidden layer have been determined through a trial-and-error process due to the absence of relevant guidelines. This trial-and-error process indicated that the use of two hidden layers comprising nine neurons each produces a satisfactory solution for the purposes of the present work, whereas the types of activation functions adopted are provided in Table 2 which also shows the layers, where the functions were incorporated. The values of the weights (wkj) and bias (Θj) are initially randomly assigned, but obtain their final values through an iterative training (calibration) process (described later) which aims at reducing to an acceptable value the difference between the output values Oi (obtained from the ANN) and the target values Ti (provided in the database) (Svozil et al. 1997; Basheer and Hajmeer 2000). A measure of the deviation of Oi from Ti is obtained from:

$$E = ( 1/ 2)\sum (T_{i} - O_{i} )^{ 2} .$$
(13)
Fig. 4
figure 4

Architecture of ANN adopted

Full size image
Fig. 5
figure 5

Flowchart describing the process through which ANNs are developed

Full size image
Table 2 Activation functions used in the ANN models
Full size table

Convergence is considered to be achieved when E becomes smaller than an acceptable value.

Experimental database

In the present study, two databases (DB) are formed which are presented as supplementary material at the end of this paper: DB-I, containing test data obtained from tests on 609 on RC beam specimens without stirrups (BWOS) (see Table A1 presented as supplementary material) and DB-II, containing test data obtained from tests on 306 RC beam specimens with stirrups (BWS) (see Table A2 presented as supplementary material). Both databases include parameters associated with the design of the RC beams as well as aspects of RC structural response at ULS (load-bearing capacity and mode of failure). All specimens are simply supported and subjected to 3 or 4 points bending tests. Table 3 provides statistical information, essential for the development of the ANNs, on the variation of certain key parameters associated with the design details and load-carrying capacity of the specimens in DB-I and DB-II.

Table 3 Statistical information concerning the test data included in DB-I AND DB-II
Full size table

Selection of input parameters

The relationship between two parameters (in the databases) is expressed through the Pearson’s correlation coefficient (r) described by Eq. (14) (Mojtaba et al. (2013)):

$$r = \frac{n\varSigma xy - (\varSigma x)(\varSigma y)}{{\sqrt {n(\varSigma x^{2} ) - (\varSigma x)^{2} } \sqrt {n(\varSigma y^{2} ) - (\varSigma y)^{2} } }},$$
(14)

where n represents the total number of samples and x, y are the two variables considered.

Tables 4 and 5 describe the correlation between the parameters considered by the ANN employed. The linear correlation coefficient (r) can obtain values between 1 and − 1 (1 > r > − 1). Negative values of r describe an inverse relation between the two associated parameters (i.e., an increase in the value of one parameter results in the decrease in the value of the other). Positive values of r have a similar effect on the values of the associated parameters (i.e., an increase in the value of one parameter results in an increase of the other). Higher absolute values of |r| indicate a more pronounced relation between the two parameters considered. Depending on r and on the basis of current knowledge on RC structural response at ULS, different combinations of input parameters are selected for the case of the beams without and with stirrups, as shown in Tables 6 and 7.

Table 4 Values of r expressing the effect between parameters considered in the database for the case of beams without stirrups
Full size table
Table 5 Values of r expressing the effect between parameters considered in the database for the case of beams with stirrups
Full size table
Table 6 Architecture of ANN models
Full size table
Table 7 Results of different ANN models
Full size table

Normalization of database

Expressing the parameters considered in the database in a non-dimensional form is of particular significance for the calibration and overall function of the ANNs, since this improves their ability to provide accurate predictions. To avoid problems associated with low learning rates of the ANNs, it is more effective to further normalize the values of the parameters between appropriate upper and lower limiting values. Furthermore, to compensate for the fact that purely experimental databases are characterized by regions (often located at their boundaries) which may not be as densely populated with data as other regions, it is considered more effective to normalize the values of the parameters considered between (0.1, 0.9) instead of (0, 1), through the use of the following expression (Krogh and Vedelsby 1995; Utans et al. 1995; Castellano and Fanelli 2000):

$$X = \left( {\frac{0.8}{{x_{\hbox{max} } - x_{\hbox{min} } }}} \right)x + \left[ {0.9 - \left( {\frac{0.8}{{x_{\hbox{max} } - x_{\hbox{min} } }}} \right)x_{\hbox{max} } } \right],$$
(15)

where xmax and xmin represent the minimum and maximum values of a specific parameter included in the database considered.

Training process

The training of the ANNs is achieved through the multi-layer free-forward back-propagation (MLFFBP) process (Beale et al. 2015) (a schematic representation of which is provided in Fig. 6) and the provided databases DB-I and DB-II. The MLFFBP process consists of two phases: (1) the free-forward phase (input signal) and (2) the back-propagation phase (error signal). In the case of the free-forward phase, the information provided is processed from the input layer towards the output layer, where the predicted solution of the problem considered is obtained. If convergence is not achieved [i.e., the difference between the output (predicted) and target (database) values is expressed by E as defined by Eq. (13)] is larger than a predefined acceptable value), then the values of the weights and bias are re-adjusted through the “gradient descent” method in which the change in weights (Δwkj) is expressed in the form:

$$\Delta w_{kj} = - \,\alpha \frac{\partial E}{{\partial w_{kj} }},$$
(16)

where a is the learning rate.

Fig. 6
figure 6

Representation of a multi-layer feed forward NN (MLFNN)

Full size image

High values of learning rate (α) result in the values of the weights (wjk) changing more drastically (large values of Δwjk) during each iteration. This can result in the training process not converging to the most optimum combination of values of weights for which the error attains its minimum value for the whole database considered (global minima). Small values of α result in small changes to the weights (wjk) (i.e., small values of Δwjk) for each iteration. In the latter case, although more training time is required (due to the larger number of iterations that have to be carried out to satisfy the convergence criteria), the iterative process is able to identify more effectively the optimum combination of values wjk for which the error function obtains its minimum value for the whole database considered allowing the ANN to provide more accurate predictions. To facilitate this process, the values of Δwkj calculated for each iteration (n > 1) are provided as a function of the corresponding adjustment carried out in the previous iteration (n − 1) and the momentum factor (0 < η <1) as follows:

$$\Delta w_{kj}^{n} = \alpha \times y_{k} + \eta \times \Delta w_{kj}^{n - 1} .$$
(17)

The selection of the most accurate of the ANN models in Table 7 is based on assessing the correlation factor (R), the mean squared error (MSE), and the mean absolute error (MAE) which are analytically expressed by Krogh and Vedelsby (1995), Utans et al. (1995) and Castellano and Fanelli (2000):

$$R = \frac{{\mathop \sum \nolimits_{i = 1}^{n} (T_{i} - \overline{T} )(O_{i} - \overline{O} )}}{{\mathop \sum \nolimits_{1}^{n} (T_{i} - \overline{T} )^{2} \mathop \sum \nolimits_{1}^{n} (O_{i} - \overline{O} )^{2} }},$$
(18a)
$${\text{MSE}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} (T_{i}^{2} - O_{i}^{2} )}}{n},$$
(18b)
$${\text{MAE}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left| {T_{i} - O_{i} } \right|}}{n},$$
(18c)

where \(\overline{T} = \mathop \sum \nolimits_{1}^{n} T_{i} /n\) and \(\overline{O} = \mathop \sum \nolimits_{1}^{n} O_{i} /n\) are the mean Ti and Oi values, respectively, and n is the total number of samples in databases, i.e., DB-I and DB-II (see Tables A1 and A2 which provided in the form of supplementary material).

During the calibration process, the normalized data are divided into three sub-sets. Each of these sub-sets is employed for training, validation, and testing purposes. Matlab (Beale et al. 2015) is used to develop the ANN models and to randomly divide the database into the three sub-sets: 60% of the data for training, 20% for validation, and 20% for testing (Krogh and Vedelsby 1995; Utans et al. 1995; Castellano and Fanelli 2000). Each ANN model is trained until one of the following conditions is met as proposed by the Levenberg–Marquardt back-propagation method (Beale et al. 2015):

  1. 1.

    For 100 iterations (epochs) including the full MLFFBP process.

  2. 2.

    Maximum of 6 validation failures are exhibited. Validation failure occurs when the performance of the ANN (assessed during each iteration) fails to improve or remains constant.

  3. 3.

    The values of performance goal indicators, expressing the difference between the target and output values (see Eqs. 18a–18c) attain small values (e.g., 10−6), indicating that convergence has been achieved.

  4. 4.

    Minimum performance gradient (related to the rate at which the weights are adjusted through the MLFFBP process) becomes 10−10.

A number of ANN models have been presently considered employing different parameters, activation functions, and number of hidden neurons and layers (see Table 6) to study their effect on the ability of the subject models to provide accurate predictions. The values of the input and output parameters are normalized between 0.1 and 0.9 at the start of the training process, whereas the values of the weight and biases vary between − 1.0 and 1.0, at the end of the training process. The previous work (Ahmad et al. 2016) has revealed that in such cases, the use of (1) the sigmoid activation function between the first three layers of the ANN (e.g., the input and the two hidden layers) and (2) the hyperbolic (tanh) activation function between the second hidden layer and the output layer allows the ANN to provide accurate predictions (see Tables 2 and 6).

A total of six different ANN models are developed for the case of the RC beams without stirrups (BWOS) and eight ANN models for the case of the RC beams with stirrup (BWS) (as described in Table 6). Table 7 presents statistical information concerning the level of correlation achieved between the predicted values of load-carrying capacity obtained from the ANN models and their experimentally established counterparts. Figures 7 and 8 show the same statistical information in the form of graphs. The ANN model considered to provide the most accurate predictions is that exhibiting the highest value of R (correlation function) in combination with the lowest values of MSE and MAE (Basheer and Hajmeer 2000). Figure 7b provides the values of R, MSE, and MAE calculated for the different ANN models developed for database DB-I (including beams without stirrups). From Table 7 and Fig. 8, it is observed the BWOS-4 exhibited the highest value of R (99.2%) in combination with the smallest values of MSE (0.05%) and MAE (1.5%), while, at the same time, employing the smallest number of parameters (i.e., d, av/d, Mf/fcbd2, and fc). Similarly, based on the information provided in Table 7 and Fig. 8 for the case of database DB-II (including beams with stirrups), BWS-8 is the most efficient ANN model (with R = 99.2%, MSE = 0.08%, and MAE = 1.9%) and employs only seven parameters (i.e., d, b/d, av/d, Mf/fcbd2, fc, and ρw × fyw).

Fig. 7
figure 7

a Predictions obtained from different ANNs for the case of RC beam specimens without stirrups (BWOS). b Performance exhibited by ANNs models for the RC beams without stirrups (BWOS)

Full size image
Fig. 8
figure 8

a Predictions obtained from different ANNs for the case of RC beam specimens with stirrups (BWS). b Performance exhibited by ANNs models for the RC beams with stirrups (BWS)

Full size image

In view of the above, ANN models BWOS-4 and DWS-8 have been selected for use in what follows.

Comparative study

A comparative study between the predicted values of load-carrying capacity obtained from the ANNs, the design codes, and their experimentally established counterparts (forming the databases) is presented in Figs. 9, 10, 11 and 12 for the case of RC beams without (BWOS) and with (BWS) stirrups, respectively, and Table 8. From Table 8, it can be seen that the ANN technique produced the closest fit to the experimental values with the smallest standard deviation, with the deviation of the mean normalized values of load-carrying capacity from unity being 0% and 1% for the cases of RC beams without and with transverse reinforcement, respectively. The code predicted mean normalized values have been found to be conservative for both types of beams in all but one case, that of the NZ code for beams with stirrups, for which the predicted value overestimates its experimental counterpart by 8%. For the case of beams without transverse reinforcement, the code predicted mean normalized values deviate from unity by an amount ranging between approximately 27% and 60%, with the EC2 and NZ code values exhibiting the smaller and larger deviations, respectively. For the case of beams with transverse reinforcement, the corresponding deviations range between approximately 14% and 53%, with EC2 and JSCE values exhibiting the smaller and larger deviations, respectively. As regards the CFP method, this produces values which deviate from unity by an amount of the order of 12% for both types of beams considered (with and without stirrups). The trends of behaviour discussed above are presented in a graphical form in Figs. 9, 10, 11 and 12.

Fig. 9
figure 9

Comparison between the predictions obtained from the various assessment methods employed and the ANN with their experimental counterparts for the case of beams without stirrups (BWOS)

Full size image
Fig. 10
figure 10

a Curves describing the normal distribution of VEXP/VPRED for beams without stirrups (BWOS) based on the predictions obtained from the various assessment methods employed and the use of ANNs. b Distribution VEXP/VPRED for beams without stirrups (BWOS) based on the predictions obtained from the various assessment methods employed and the use of ANNs

Full size image
Fig. 11
figure 11

Comparison between the predictions obtained from the various assessment methods employed and the ANN with their experimental counterparts for the case of beams with stirrups (BWS)

Full size image
Fig. 12
figure 12

a Curves describing the normal distribution of VEXP/VPRED for beams with stirrups (BWS) based on the predictions obtained from the various assessment methods employed and the use of ANNs. b Distribution VEXP/VPRED for beams with stirrups (BWS) based on the predictions obtained from the various assessment methods employed and the use of ANNs

Full size image
Table 8 Results of VExp/VPred for RC beams
Full size table

It should be noted at this stage that, unlike the other methods investigated, the CFP method is, by nature, capable of providing close predictions of not only the values of load-carrying capacities, but also of the locations and the causes of failure. In fact, the predictions of the latter have been successful in all cases investigated in the present work. Naturally, similar predictions cannot be expected to be obtained from a purely empirical method such as the ANN technique employed in the present work, which, however, has been found capable of producing the best possible numerical predictions of load-carrying capacity.

It is also important to note that, as already discussed, the code methods are also heavily dependent on the use of experimental data for the calibration of the formulae underlying the assumed mechanisms of load transfer. The use of the code-adopted formulae, when compared with the use of the ANN technique employed in the present work, appears to reduce the effectiveness of the calibration process and this may be considered to reflect shortcomings of the underlying theory in describing the actual mechanism of load transfer. On the other hand, the ability of the CFP method to produce numerical predictions exhibiting a relatively small deviation from those resulting from the ANN procedure, without the need of prior calibration, may be considered as an indication of the validity of the concepts underlying the method.

Conclusions

The accuracy of the predictions of the RC design methods considered is assessed primarily against the available test data. The calibrated ANNs developed were successful in providing predictions very close to their experimentally established counterparts. The good correlation between the available test data and the predictions of the ANNs demonstrate that the latter soft computing method provides an effective tool capable of objectively analyzing the available test data and quantifying the effect of specific parameters on certain important characteristics of RC structural behaviour (e.g., the load-carrying capacity and mode of failure)

The ANN procedure, which is purely empirical in nature and follows a detailed mathematical approach within a heuristic scheme allowing for all parameters widely assumed to affect load-carrying capacity, is found to produce a nearly perfect fit to the test data available in the literature on shear capacity of simply supported beam/column elements.

Current code methods for calculating shear capacity are semi-empirical in that, unlike the ANN procedure, the test data are used for calibrating the formulation of the theoretical basis of the methods. The resulting formulae are found conservative: they underestimate shear capacity by an amount ranging between approximately 15% and 60%.

The inability of the code methods to provide a fit to the test data as close as that of the ANN procedure is considered to reflect the lack of effectiveness of the code formulae to describe the trends of behaviour exhibited by the test data and this may be viewed as an indication of shortcomings of the theoretical basis of the code-design methods.

In contrast with code methods, the formulation of the theoretical basis of the CFP method does not require calibration through the use of test data. The failure criteria have been derived from first principles and are functions of the strength of concrete of uniaxial compression and tension. Moreover, unlike the code methods, the CFP is capable of identifying both the location and the causes of failure.

An indication of the validity of the method is provided not only by the fit to the test data which is nearly as close as that of the ANN procedure for the case of simply supported beams, but also by the realistic predictions of the load-carrying capacity, location, and causes of failure of the structural elements exhibiting points of contra-flexure. However, since test data on the behaviour of the latter structural elements are rather sparse, additional work is required for drawing definitive conclusions on the method.