Abstract
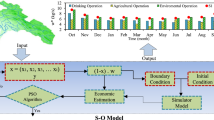
In this paper, a probabilistic water quality management model is developed to present strategies using bankruptcy rules for solving conflicts between the Environmental Protection Agency and polluters in river systems. The bankruptcy concepts are adapted to the water quality aspect, Dissolved Oxygen as the water quality factor, and the pollutant concentration refers to the asset and stakeholders' claim. Bankruptcy rules are developed to allocate wastewater cooperatively and improve the water quality at the checkpoint. Therefore, a simulation–optimization model, including QUAL2Kw and Particle Swarm Optimization, is used to optimize the bankruptcy method’s waste load allocation. In the probabilistic model, the effect of river flow uncertainty on the optimal solution is investigated by Monte Carlo and Latin Hypercube Sampling. The optimal Dissolved Oxygen values are obtained corresponding to the possibility of river flows under the bankruptcy rules. The results of deterministic and probabilistic models show that the methodology reduces the waste load by 65–94% and increases Dissolved Oxygen from 0.9 to 5 mg/L. However, the streamflow uncertainty benefits polluters and allows them to release pollution more than twice the deterministic model. Analyzing the rules reveals that the Talmud rule outperformed others with higher Dissolved Oxygen and waste load criterion. This reliable probabilistic model can be used when the parties' performance is not cooperative, leading to more adaptability with real situations.








Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Abed-Elmdoust A, Kerachian R (2012) River water quality management under incomplete information: application of an N-person iterated signaling game. Environ Monit Assess 184(10):5875–5888. https://doi.org/10.1007/s10661-011-2387-x
Aghasian K, Moridi A, Mirbagheri A, Abbaspour M (2019) A conflict resolution method for waste load reallocation in river systems. Int J Environ Sci Technol 16(1):79–88. https://doi.org/10.1007/s13762-018-1993-3
Anile AM, Cutello V, Nicosia G, Rascuna R, Spinella S (2005) Comparison among evolutionary algorithms and classical optimization methods for circuit design problems. IEEE Congress Evol Comput 1:765–772. https://doi.org/10.1109/cec.2005.1554760
Ansink E, Weikard HP (2012) Sequential sharing rules for river sharing problems. Social Choice Welf 38(2):187–210. https://doi.org/10.1007/s00355-010-0525-y
Bowers MC, Tung WW, Gao JB (2012) On the distributions of seasonal river flows: lognormal or power law? Water Resour Res. https://doi.org/10.1029/2011WR011308
Bozorg-Haddad O, Athari E, Fallah-Mehdipour E, Loáiciga HA (2018) Real-time water allocation policies calculated with bankruptcy games and genetic programing. Water Sci Technol Water Supply 18(2):430–449. https://doi.org/10.2166/ws.2017.102
Burn DH, Lence BJ (1992) Comparison of optimization formulations for waste-load allocations. J Environ Eng 118(4):597–612. https://doi.org/10.1061/(asce)0733-9372(1992)118:4(597)
Burn DH, McBean EA (1985) Optimization modeling of water quality in an uncertain environment. Water Resour Res 21(7):934–940
Burn DH, McBean EA (1986) Linear stochastic optimization applied to biochemical oxygen demand–dissolved oxygen modelling. Can J Civ Eng 13(2):249–254. https://doi.org/10.1139/l86-033
Clerc M (2006) Particle swarm optimization. ISTE, London
Degefu DM, He W, Yuan L, Min A, Zhang Q (2018) Bankruptcy to surplus: sharing transboundary river basin’s water under scarcity. Water Resour Manage 32(8):2735–2751. https://doi.org/10.1007/s11269-018-1955-z
Estalaki SM, Abed-Elmdoust A, Kerachian R (2015) Developing environmental penalty functions for river water quality management: application of evolutionary game theory. Env Earth Sci 73(8):4201–4213. https://doi.org/10.1007/s12665-014-3706-7
Ghorbani Z, Amanipoor H, Battaleb-Looie S (2020) Water quality simulation of Dez River in Iran using QUAL2KW model. Geocarto Int 8:1–3. https://doi.org/10.1080/10106049.2020.1762763
Herrero C, Villar A (2001) The three musketeers: four classical solutions to bankruptcy problems. Math Social Sci 42(3):307–328. https://doi.org/10.1016/S0165-4896(01)00075-0
IWPC (Iran's Water and Power Resources Development Company) )2013( Available in Persian. Technical Rep., IWPC Research Dep., Tehran, Iran.
Janjua S, Hassan I (2020) Transboundary water allocation in critical scarcity conditions: a stochastic bankruptcy approach. J Water Supply Res Technol AQUA 69(3):224–237. https://doi.org/10.2166/aqua.2020.014
Kampas A, White B (2003) Selecting permit allocation rules for agricultural pollution control: a bargaining solution. Ecol Econ 47(2–3):135–147. https://doi.org/10.1016/S0921-8009(03)00195-2
Kannel PR, Lee S, Lee YS, Kanel SR, Pelletier GJ (2007) Application of automated QUAL2Kw for water quality modeling and management in the Bagmati River, Nepal. Ecol Model 202(3–4):503–517. https://doi.org/10.1016/j.ecolmodel.2006.12.033
Langat PK, Kumar L, Koech R (2019) Identification of the most suitable probability distribution models for maximum, minimum, and mean streamflow. Water 11(4):734. https://doi.org/10.3390/w11040734
Li S, He Y, Chen X, Zheng Y (2020) The improved bankruptcy method and its application in regional water resource allocation. J Hydro-Environ Res 28:48–56. https://doi.org/10.1016/j.jher.2018.07.003
Liebman JC, Lynn WR (1966) The optimal allocation of stream dissolved oxygen. Water Resour Res 2(3):581–591. https://doi.org/10.1029/WR002i003p00581
Liu D, Guo S, Shao Q, Jiang Y, Chen X (2014) Optimal allocation of water quantity and waste load in the Northwest Pearl River Delta, China. Stoch Env Res Risk Assess 28(6):1525–1542. https://doi.org/10.1007/s00477-013-0829-4
Madani K, Hipel KW (2011) Non-cooperative stability definitions for strategic analysis of generic water resources conflicts. Water Resour Manage 25(8):1949–1977. https://doi.org/10.1007/s11269-011-9783-4
Madani K, Lund JR (2012) California’s Sacramento-San Joaquin delta conflict: from cooperation to chicken. J Water Resourc Plan Manage 138(2):90–99. https://doi.org/10.1061/(ASCE)WR.1943-5452.0000164
Madani K, Zarezadeh M (2012) Bankruptcy methods for resolving water resources conflicts. In: Proceedings of the 2012 congress world environmental and water resources congress 2012: Crossing Boundaries, pp 2247–2252. doi: https://doi.org/10.1061/9780784412312.226.
Madani K, Sheikhmohammady M, Mokhtari S, Moradi M, Xanthopoulos P (2014) Social planner’s solution for the Caspian Sea conflict. Group Decis Negot 23(3):579–596. https://doi.org/10.1007/s10726-013-9345-7
Madani K, Zarezadeh M, Morid S (2014) A new framework for resolving conflicts over transboundary rivers using bankruptcy methods. Hydrol Earth Syst Sci 18(8):3055. https://doi.org/10.5194/hess-18-3055-2014
Manache G, Melching CS (2004) Sensitivity analysis of a water-quality model using Latin hypercube sampling. J Water Resour Plan Manage 130(3):232–242. https://doi.org/10.1061/(ASCE)0733-9496(2004)130:3(232)
Mesbah SM, Kerachian R, Nikoo MR (2008) Developing real time operating rules for trading discharge permits in rivers: application of bayesian networks. Environ Model Softw 24(2):238–246. https://doi.org/10.1016/j.envsoft.2008.06.007
Mianabadi H, Mostert E, Zarghami M, van de Giesen N (2014) A new bankruptcy method for conflict resolution in water resources allocation. J Environ Manage 144:152–159. https://doi.org/10.1016/j.jenvman.2014.05.018
Moreno-Ternero JD, Villar A (2006) The TAL-family of rules for bankruptcy problems. Soc Choice Welf 27(2):231–249
Moridi A (2019) A bankruptcy method for pollution load reallocation in river systems. J Hydroinf 21(1):45–55. https://doi.org/10.2166/hydro.2018.156
Nikoo MR, Kerachian R, Karimi A, Azadnia AA (2013) Optimal water and waste-load allocations in rivers using a fuzzy transformation technique: a case study. Environ Monit Assess 185(3):2483–2502. https://doi.org/10.1007/s10661-012-2726-6
Pebesma EJ, Heuvelink GB (1999) Latin hypercube sampling of Gaussian random fields. Technometrics 41(4):303–312. https://doi.org/10.1080/00401706.1999.10485930
Pelletier GJ, Chapra SC, Tao H (2006) QUAL2Kw–A framework for modeling water quality in streams and rivers using a genetic algorithm for calibration. Environ Model Softw 21(3):419–425. https://doi.org/10.1016/j.envsoft.2005.07.002
Rajabi MM, Ataie-Ashtiani B, Janssen H (2015) Efficiency enhancement of optimized Latin hypercube sampling strategies: application to Monte Carlo uncertainty analysis and meta-modeling. Adv Water Resour 76:127–139. https://doi.org/10.1016/j.advwatres.2014.12.008
Rini DP, Shamsuddin SM, Yuhaniz SS (2011) Particle swarm optimization: technique, system and challenges. Int J Comput Appl 14(1):19–26. https://doi.org/10.5120/1810-2331
Saberi L, Niksokhan MH (2017) Optimal waste load allocation using graph model for conflict resolution. Water Sci Technol 75(6):1512–1522. https://doi.org/10.2166/wst.2016.429
Shojaei M, Nazif S, Kerachian R (2015) Joint uncertainty analysis in river water quality simulation: a case study of the Karoon River in Iran. Environ Earth Sci 73(7):3819–3831. https://doi.org/10.1007/s12665-014-3667-x
Steyvers M (2011) Computational statistics with MATLAB. University of California, Irvine, psiexp.ss.uci.edu/research/teachingP205C205.
Warwick JJ, Roberts LA (1992) Computing the risks associated with wasteload allocation modeling 1. JAWRA J Am Water Resour Assoc 28(5):903–915. https://doi.org/10.1111/j.1752-1688.1992.tb03191.x
Wei S, Gnauck A (2007) Water supply and water demand of Beijing—a game theoretic approach for modeling. Inf Technol Environ Eng. https://doi.org/10.1007/978-3-540-71335-7_51
Zeng Y, Li J, Cai Y, Tan Q (2017) Equitable and reasonable freshwater allocation based on a multi-criteria decision making approach with hydrologically constrained bankruptcy rules. Ecol Ind 73:203–213. https://doi.org/10.1016/j.ecolind.2016.08.049
Zolfagharipoor MA, Ahmadi A (2017) Effluent trading in river systems through stochastic decision-making process: a case study. Environ Sci Pollut Res 24(25):20655–20672. https://doi.org/10.1007/s11356-017-9720-z
Acknowledgements
This research is based on the results of an MSc thesis at Shahid Beheshti University, Tehran, Iran.
Funding
This research has been supported by the research grant no. 600/1181 funded by Shahid Beheshti University, Tehran, Iran.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Editorial responsibility: S.R. Sabbagh-Yazdi.
Rights and permissions
About this article
Cite this article
Farjoudi, S.Z., Moridi, A., Sarang, A. et al. Application of probabilistic bankruptcy method in river water quality management. Int. J. Environ. Sci. Technol. 18, 3043–3060 (2021). https://doi.org/10.1007/s13762-020-03046-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13762-020-03046-8