Abstract
With the acceleration of global climate change and urbanization, disaster chains are always connected to artificial systems like critical infrastructure. The complexity and uncertainty of the disaster chain development process and the severity of the consequences have brought great challenges to emergency decision makers. The Bayesian network (BN) was applied in this study to reason about disaster chain scenarios to support the choice of appropriate response strategies. To capture the interacting relationships among different factors, a scenario representation model of disaster chains was developed, followed by the determination of the BN structure. In deriving the conditional probability tables of the BN model, we found that, due to the lack of data and the significant uncertainty of disaster chains, parameter learning methodologies based on data or expert knowledge alone are insufficient. By integrating both sample data and expert knowledge with the maximum entropy principle, we proposed a parameter estimation algorithm under expert prior knowledge (PEUK). Taking the rainstorm disaster chain as an example, we demonstrated the superiority of the PEUK-built BN model over the traditional maximum a posterior (MAP) algorithm and the direct expert opinion elicitation method. The results also demonstrate the potential of our BN scenario reasoning paradigm to assist real-world disaster decisions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A disaster chain refers to the phenomenon that a series of secondary disasters are caused by a certain primary disaster, forming a complex process of disaster transmission and amplification (Shi 1996). As an illustration, the Wenchuan Earthquake brought about several severe disasters such as secondary collapse, landslides, and debris flows, while Typhoon Lekima caused rainstorms and floods, residential structure damage, power failure, and so on. Disaster chains show uncertainty, ambiguity, and randomness. In addition, emergency decision makers may get increasingly perplexed and fail to make the best decisions due to the complexity of various disasters and the heterogeneity of information from several sources. The scenario-based decision-making methodology has been widely used to address this issue, improve the readiness for disaster chains, and take proactive actions (Moehrle and Raskob 2015). Scenario reasoning helps to analyze the disaster developing process and review existing emergency response capabilities. A scenario-response paradigm can be an improvement over the conventional prediction-response paradigm, effectively increase disaster awareness, and enhance the ability to make emergency decisions (Zhang and Liu 2012).
Disaster scenario reasoning can answer inquiries such as “What is the situation now?” and “What if the situation persists?” (Alexander 2013). There are three types of scenario reasoning methods for emergency management: case-based, simulation-based, and network-based (Liu et al. 2018). Network-based methods are particularly widely used in disaster chains (Sakahira and Hiroi 2021). These methods model the relationship between disaster-related elements in a networked manner, where elements like disaster events and response measures are nodes and correlations and causal relations are links. The Bayesian network (BN) is one of the probabilistic graphical models that define the interaction between nodes (a group of variables) as a directed edge of a conditional probability distribution. The use of BN in conjunction with the scenario analysis method to establish scenario reasoning based on probability calculation has become a research hotspot in the field of emergency management in recent years. To predict and examine the chain reaction path and possible losses of rainstorm situations, Qiu et al. (2014) suggested a BN-based modeling method. A quantitative multi-risk management model using BNs was put forth by Liu et al. (2014) to assess the cascading hazard of the tsunami triggered by a rockslide. Comes et al. (2015) introduced group decision theory and multi-attribute decision theory into the construction of a Bayesian network to get the opinions of domain experts on the development trend of uncertain disasters. Han et al. (2019) combined the BN and the ArcGIS software to create a hazard chain assessment model for the Changbai Mountains in China. When fresh evidence (beliefs, monitoring data), which may be updated by users using BNs, appears in a particular node, they can update not just the final outcomes but also all the information in the network (Hosseini and Ivanov 2020). By capturing the model’s uncertainty in this manner, the BN offers a nearly real-time scenario reasoning process.
In emergency decision-making research, the structure of BN is usually determined relying on expert knowledge since the algorithm might not be able to accurately identify and simulate hazards and their interactions (Chen and Pollino 2012). It is known that the graphical structure’s complexity and dependability are essential components to its success. However, the more complex the structure of a BN is, the more difficult it is to learn the parameters (the conditional probability tables, CPTs). On the one hand, for emergencies, datasets are often sparse, which lowers the precision of parameter estimates. On the other hand, it is challenging for the experts to deliver precise quantitative CPTs. A workable solution to this problem is to combine parameter learning with additional knowledge provided by experts (Zhou et al. 2016; Hou et al. 2020). Various methods have been created to include more qualitative constraints by domain expert knowledge. Convex optimization (de Campos and Ji 2008) introduces constrained parameter spaces or penalty functions. In the limited parameter space of the maximum a posterior (MAP) algorithm, aualitative maximum a posterior (QMAP) creates a Dirichlet priori from a Monte Carlo random sample (Chang and Wang 2010). The QMAP methods exhibit good estimation outcomes, assuming that it is possible to obtain all convex parameter constraints. However, practically speaking, this assumption is nearly impossible. It is frequently difficult to properly prepare for these comprehensive constraint sets because of the complexity of BNs in relation to emergencies and the limitations of domain knowledge cognition.
In this study, to leverage expert-based information, we provided an algorithm for parameter learning—parameter estimation under expert prior knowledge (PEUK). The prior knowledge of CPTs is obtained from direct elicitation by asking experts to give confidence intervals using a probability scale. Then the maximum entropy principle is applied to balance expert knowledge and parameter learning. When the data learning outcomes perform better in the test set, PEUK tends toward the traditional MAP method; otherwise, it tends toward expert prior knowledge. Building on this proposed algorithm, we formalized our disaster chain scenario reasoning solution with a Bayesian network. A scenario representation model of disaster chains—the hazard, emergency, hazard-affected object, emergency response measure, consequence (HEOMC) framework—was developed, and the rainstorm chain was taken as an example to show the construction process of the model. With the scenario representation model, the configuration, training, and application of a Bayesian network for scenario analysis and decision support are described. Our work offers two contributions: (1) Using a flexible and extensible BN model, a scenario representation model is created that improves our ability to simulate a disaster chain and provides a more practical level of preparedness; (2) By combining expert previous knowledge and case data, the PEUK algorithm innovates the BN parameter learning process.
The rest of this article is divided into the following sections. Section 2 proposes the disaster chain scenario representation model. Section 3 describes how to generate a BN for scenario reasoning and illustrates the benefits of the PEUK parameter learning algorithm. Section 4 discusses the impact of our method on the practice of the scenario-response based disaster response strategy. Section 5 concludes the article by considering potential paths for additional research.
2 Representation Model for Disaster Chain Scenario
Scenario is initially a depiction of a future condition and a tendency for an event to change from its current state to a future one. Recently, customizing scenario’s definition and representation has gained more attention in emergency management. Comes et al. (2011, 2015) defined scenario as a specific emergency circumstance, as well as its growth and effects. Wu et al. (2013) defined scenario as an ordered collection of distinct instances that includes a description of the environment, context, actors, and actions.
The purpose of emergency management is to help decision makers protect items from catastrophe damage (Fan et al. 2013). The effective collection of information about the affected objects and the disaster chain damages is the only way to make sound decisions. As a result, creating a representation model for each damaged object of the disaster chain is a critical effort in creating scenarios.
2.1 The Hazard, Emergency, Hazard-Affected Object, Emergency Response Measure, Consequence (HEOMC) Representation Model
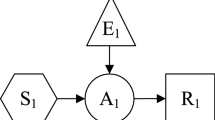
Considering a hazard affecting an object as a basic event, a disaster chain scenario in this study has five elements: initial hazard (denoted by H), emergency event (denoted by E), hazard-affected object (denoted by O), emergency response measure (denoted by M), and consequence (denoted by C). We formalized our disaster chain scenario construction method as the HEOMC framework, as seen in Fig. 1. Figure 1a shows the relationship between these five elements, and their detailed definitions are as follows:
-
(1)
Initial hazard (H) A source of initial danger in the natural or human-made environment that can adversely affect human life, property, or various activities. In this study, rainstorm is taken as the initial hazard.
-
(2)
Emergency (E) An event that occurs when a hazard-affected object is acted upon by a hazard, such as a geologic hazard, waterlogging, landslide, and so on.
-
(3)
Hazard-affected object (O) Spatial entities that are directly influenced by hazards, such as construction sites, water conservancy facilities, urban transportation infrastructure, people, and so on.
-
(4)
Emergency response measure (M) Measures that are taken to control hazards and eliminate their influence on objects, which can be divided into two types—precautions and rescue measures.
-
(5)
Consequence (C) Injuries and deaths, and property losses caused by hazards.
The disaster chain can be identified either through the causal relationship between successive occurrences of disaster events (Yu et al. 2020; Yu et al. 2023) or based on the spatial correlation of disasters (Balbi et al. 2016; Zhong et al. 2017). In our study, a disaster chain scenario can be represented as a combination of these five elements: \({S}_{i}=\{{H}_{0},{O}_{i},{E}_{i},{M}_{i},{O}_{ij},{E}_{ij},{M}_{ij},{O}_{ijk},{E}_{ijk},\cdots ,C\}\). We disentangle the complex spatial and temporal relationships among disaster chains through hazard-affected objects, where hazards or emergencies act on different hazard-affected objects, leading to new emergencies or different disaster consequences. For instance, when a rainstorm acts on geological hazard zones, a new emergency caused by mudslide may occur and acts on roads, causing road damage, which can be regarded as a disaster chain; a rainstorm directly acts on the road and causes ponding and circuit breaking, which can be regarded as another disaster chain. Figure 1b shows a representation of disaster chains.
2.2 Rainstorm Chain Scenario Diagram
Based on the HEOMC framework, we took rainstorm as the initial hazard, analyzed its influence on various objects, and identified disaster chains to construct a scenario for the rainstorm. Six hazard-affected objects are considered, including construction sites, urban transportation infrastructure, old bungalows and low-lying yards, water conservation facilities, geological hazard zones, and mining areas. Correspondingly, possible induced emergencies include waterlogging, houses flooded and collapsed, floods, mudslides, dam breaks, and so on.
First, the rainstorm may cause floods in rivers and lakes. In this situation, the emergency response measure for water conservation facilities is to strengthen water regime monitoring, carry out water resources dispatching, and strengthen facility patrol and protection; the emergency response measure for the hazard flood is to strengthen flood regulation, repair river embankments, and block crevasse. The floods may further affect urban lifeline systems, houses, and unevacuated residents, causing secondary disasters, economic losses, and casualties. When the flood acts on lifeline systems, it may result in a cut-off of water, power, and gas supplies, further affecting the normal lives of urban residents. In this case, the emergency response measures include strengthening pipeline patrol and reinforcement, adjusting supply routes, repairing damaged pipelines, communicating with the affected residents, and taking emergency protection measures. Similarly, we identified the scenario composition of other rainstorm-induced disaster chains to generate a complete scenario structure diagram of the rainstorm, as shown in Fig. 2. The legends of Fig. 2 are shown in Table 1.
3 Bayesian Network Construction of Rainstorm Chain Scenario
Generally, there are three steps to create a Bayesian network (BN) for a problem domain: (1) Identify the BN variable and its state classification; (2) Identify the BN structure, that is, the causal relationship between BN variables; and (3) Learn the BN parameter, that is, the conditional probability table (CPT) for each BN variable. In this study, BN variables and structure were determined based on our proposed rainstorm scenario structure; BN parameters were estimated from both case data and expert knowledge generated by questionnaire surveys and the fuzzy set theory (Zadeh 1965). Details of these processes are described in the following subsections.
3.1 Bayesian Network (BN) Variables and Structure Identification
Referring to Fig. 2, we conducted a case study of typical rainstorms and determined the BN network of the rainstorm scenario, as shown in Fig. 3. In total, 57 scenario elements (BN variables) are considered, and the details are shown in Table 2. All of these BN variables, \(\mathrm{\rm X}=\left\{{X}_{1},{X}_{2},\cdots ,{X}_{57}\right\}\), are assigned discrete values. The assignment rules are as follows:
-
(1)
Hazard Rainstorm is divided into four risk states, blue, yellow, orange, and red, based on whether hourly rainfall depth, 6-h rainfall depth, or 24-h rainfall depth reaches the threshold (30, 50, 70), (50, 70, 100), (70, 100, 150), and (100, 150, 200), and the value unit is mm. The thresholds are set according to the rainstorm warning rules for City B.
-
(2)
Emergency The first rule is to divide based on risk level. Flood is divided into two states: low risk and high risk. If the rainfall is within the disaster-inducing threshold of small and medium-sized rivers, it is coded as low risk; otherwise, it is high risk. The other rule is to divide according to whether an incident occurs or not. For example, if the construction is waterlogged, it is coded as yes; otherwise, no.
-
(3)
Hazard-affected object The first rule is to divide based on risk level. Urban transportation infrastructure is divided into three states: low risk, medium risk, and high risk. For urban transportation infrastructure, if the rainfall intensity is within the design standard of all roads, it is coded as low risk; if the rainfall intensity exceeds the branch road design standard, it is medium risk; and if the rainfall intensity exceeds the trunk road design standard, it is high risk. The other rule is based on the state of the hazard-affected object itself, that is, whether it exists, or the degree of its vulnerability. For example, lifeline systems are divided into yes or no, and the population of flood diversion areas is divided into sparse and dense.
-
(4)
Emergency response measure Based on whether the emergency response measure is carried out, it can be divided into two states: yes or no.
-
(5)
Consequence Based on whether the consequence occurs, it can be divided into two cases: yes or no.
3.2 Bayesian Network (BN) Parameter Estimation
The purpose of this section is to calculate the conditional probability \({\theta }_{ijk}=P\left({X}_{i}=k|{P}_{a}\left({X}_{i}\right)=j\right)\), which represents the likelihood that \({X}_{i}\) will take the kth value and its parent node \({P}_{a}\left({X}_{i}\right)\) will adopt the jth state configuration. A parameter learning algorithm—parameter estimation under expert prior knowledge (PEUK)—was proposed. The PEUK has three steps. First, we collect questionnaire results from experts and take advantage of the fuzzy set theory to quantify the elicited statements as conditional probabilities. Then, the classical maximum a posteriori (MAP) algorithm (Koller and Friedman 2009) is applied to estimate the conditional probabilities from case data. Third, the final conditional probabilities are calculated according to the maximum entropy principle (MEP).
3.2.1 Parameter Estimation Under Expert Prior Knowledge (PEUK) Algorithm Overview
Step 1 Calculate the expert knowledge-based parameter \({\theta }_{ijk}^{*}(K)\).
The BN nodes are classified into two categories. The first type lacks parent nodes and requires specialists to give prior probability based on professional experience, such as Node 1 (Fig. 3). The second type is represented by Node 4 (Fig. 3), whose conditional probabilities are affected by their parent nodes. We use a questionnaire survey to collect qualitative statements of CPTs, and then use the fuzzy set theory to process the results.
The numerical probability scale is used to elicit single probabilities. Experts are required to judge probabilities with a verbal description. Seven intervals are defined, see Fig. 4a. The translation of the verbal probability scale into fuzzy sets is provided in Fig. 4b (Rohmer 2020). For a fuzzy number, \(\widetilde{X}=(a,b,c)\) as seen in Fig. 5, is referred to as a triangular fuzzy number, and its membership function is defined by Eq. 1, where a, b, and c indicate the lowest, most likely, and top least likely values, respectively. Given two triangular fuzzy numbers, \({\widetilde{A}}_{1}=({a}_{1},{b}_{1},{c}_{1})\) and \({\widetilde{A}}_{2}=({a}_{2},{b}_{2},{c}_{2})\), Eq. 2 defines the operators between \({\widetilde{A}}_{1}\) and \({\widetilde{A}}_{2}\), which includes addition, subtraction, multiplication, and division.
Assuming the mth expert regards that the probability of \({\theta }_{ijk,m}^{*}\) resides in the lth interval, specified by \({\widetilde{A}}_{lm}(l=1,2,\cdots ,7)\), Eq. 3 is used to calculate the fuzzy probability of \({\theta }_{ijk,m}^{*}\). This fuzzy probability is further transformed to an exact value using the center-of-area defuzzification method by Eq. 4.
Step 2 Calculate the data-based parameter \({\theta }_{ijk}^{*}(D)\).
In the case of a large enough sample size, the maximum likelihood estimation (MLE) (Niculescu et al. 2006) is used to estimate the value of a single parameter θijk (denoted as \({\theta }_{ijk}^{*}\)) as:
where Nijk represents the number of cases in the dataset where variable Xi has the kth value and its parent, Pa(Xi), has the jth value. When a comprehensive Bayesian solution is unfeasible, the Dirichlet prior (\(P\left(\theta \right)\propto \prod_{i=1}^{n}\prod_{j=1}^{{q}_{i}}\prod_{k=1}^{{r}_{i}}{\theta }_{ijk}^{{\alpha }_{ijk}}\)) (Koller and Friedman 2009) has proposed the standard MAP algorithm to address the problem. αijk represents the equivalent sample size for Nijk, in which \({a}_{ij}={\sum }_{k=1}^{{r}_{i}}{a}_{ijk}\). The likelihood equivalent uniform Bayesian Dirichlet (EDeu) prior and the flat prior of αijk are commonly used. For a single parameter, θijk, its MAP estimate is:
In this study, we set \({\alpha }_{ijk}=\frac{1}{{r}_{i}{q}_{i}}\).
When the sample size is small, MLE is usually inaccurate. Koller and Friedman (2009) defined a method for computing the sample complexity bound (PAC-bound) for learning the parameters of a fixed BN structure:
where M is the number of samples quadratically to the error \(1/\varepsilon \), \(\lambda \) is a measure of the skewness of the distribution with the confidence \(1-\delta \), d is the maximum number of parent nodes in BN, \(\gamma \) is the KL divergence, and n is the total number of network nodes in the BN. Here \(d=4\) and \(n=57\). \(\lambda \) and \(\gamma \) are theoretical values related to the sample distribution. Our sample is discretized so that it is not possible to solve for these two values. For simplicity, both are assumed to be 1. Setting \(\varepsilon =0.05\) and \(\delta =0.01\), we get that M ≥ 1907. That is, we need a bit more than 1907 samples to confidently estimate the probability of an event to within 5% error.
Step 3 Calculate the PEUK parameter \({\theta }_{ijk}^{*}(PEUK)\).
To calculate the PEUK parameter, the maximum entropy principle (MEP) is used, with the fundamental tenet that the probability distribution that most accurately captures the current level of knowledge has the highest entropy. Based on a model using MEP, it is suggested that the parametric form for the model \(p\in C\) might be defined as follows (Berger et al. 1996):
where C is a collection of the probability distributions that satisfy the constraint requirements, and \(p(x)p(y|x)\) is the joint probability of the random variables related to events. The conditional distribution’s mathematical measure \(p(y|x)\) is supplied by the conditional entropy.
We involve M domain experts to obtain the constrained knowledge. According to MEP, if BN candidate parameters satisfy the constrained knowledge, they have an equal probability of approaching the real BN parameters. The maximum entropy principle helps to address the issue of parameter estimation in the statistical averaging model naturally. Then, for a BN parameter θijk, its estimation is:
where \(\sum_{m=1}^{M}\frac{{\theta }_{ijk,m}^{*}(K)}{M}\) is the expert knowledge-based parameter derived from MEP, and \(\xi \in \left[0,1\right]\) is the parameter weight balance factor. Here we set \(\xi =\frac{acc(K)}{acc\left(K\right)+acc(D)}\). \(acc(K)\) and \(acc(D)\) represent the prediction accuracy of BN models with parameters learned only from expert knowledge and case data, respectively. Assuming \(acc(K)\) is guaranteed at 0.8. \(acc(D)\) is related to the sample size, and the larger the sample size, the higher the \(acc(D)\). If sufficient sample data are provided, \(acc(D)\approx 1\) and \(\xi \approx 0.55\), the estimation will be more biased towards the data learning results. If the sample size is far from adequate, consider the extreme case where \(acc(D)\approx 0\), then \(\xi \approx 1\), which means the estimation will adopt the expert estimates.
3.2.2 Evaluation of the Parameter Estimation Under Expert Prior Knowledge (PEUK) Algorithm
This section evaluates our BN model with the PEUK algorithm. We compare its performance for reasoning the consequence of rainstorm with two baseline models—the BN constructed only by expert knowledge elicited from the fuzzy set theory, and the BN constructed only by data learning.
The experimental data were acquired from the investigation reports and news of rainstorm events that occurred in City B in North China in recent 60 years. One event may be divided into multiple cases according to the different administrative regions involved. In total, 122 rainstorm cases were obtained, each of which was coded by BN variables with discrete values. According to the PCA-bound theory, it is clear that as the number of the cases decreases, the inverse of the error increases quadratically. In this study, we randomly selected 98 cases (80% of all cases) as our training data to learn the data-based BN parameter \({\theta }_{ijk}^{*}(D)\).
Three experts were invited to elicit the expert knowledge-based BN parameter \({\theta }_{ijk}^{*}(K)\). These experts were from the Emergency Management Agency in City B, all of whom had been working for more than 10 years and had extensive experience with rainstorms. Besides, the homogeneity, differences, and opposites of expert knowledge were synthesized through the fuzzy set theory in order to reduce the uncertainty of individual experts.
The PEUK parameter \({\theta }_{ijk}^{*}({\text{PEUK}})\) was calculated by Eq. 9. Then, three BN models for reasoning rainstorms with different parameters were constructed, which are BNE, BND, and BNPEUK.
The other 24 cases were reserved for testing the effectiveness of these three BN models. Performance was measured by the results of nine consequence variables, including Node 6 construction sites damage, Node 15 casualties (caused by waterlogging), Node 23 casualties (caused by house collapsing), Node 32 casualties (caused by flooding), Node 37 disrupted living, Node 39 inundation and damage, Node 45 house/farmland/lifeline system damage, Node 49 casualties (caused by geological disasters), and Node 57 casualties (caused by dam break), as shown in the orange nodes in Fig. 3. The performance metrics are overall accuracy of all consequence variables, recall, precision, and F1 score.
Figure 6 shows the BN models’ prediction performance for 24 testing cases, from which we can draw the following findings:
-
(1)
BND performs the worst in terms of overall accuracy. The results of Node 49 and Node 57 show that it cannot deduce the consequences of the dam break scenario. This is consistent with our expectations since our training data are sparse and there are almost no dam break cases.
-
(2)
In terms of the results of Node 32 and Node 39, BNE performs slightly worse than the other two BN models. That is because both Node 32 and Node 39 are consequence nodes of the flood scenario, which is a common secondary event of a rainstorm. There are adequate flood cases in our training data so that the accuracy of these parameters learned from the data is high.
-
(3)
Overall, BNPEUK performs the best. BNPEUK imbibes advantages of both BND and BNE while having generalization ability for sparse variables and sufficient variables at the same time.
4 Scenario Analysis and Discussions
In this section, BNPEUK is used to analyze the effectiveness of emergency response measures. Specifically, for the six disaster chains of the rainstorm considered in this study, we compare the consequences under different scenarios composed of different emergency response measures to find out the optimal measures to reduce disaster consequences.
4.1 Scenario Analysis
-
(1)
Construction sites waterlogged
In the construction sites waterlogged disaster chain, Node 2 construction sites is the hazard-affected object, Node 4 construction sites waterlogged is the emergency, Node 3 strengthen drainage facilities and Node 5 drain floodwater and perform emergency repairs are emergency response measures, and Node 6 construction sites damage is the consequence. By adjusting the states of Node 3 and Node 5 to get different combinations of emergency response measures, four scenarios of construction sites waterlogged are obtained: S11, S12, S13, and S14. S11 indicates that no emergency response measure is taken, that is, Node 3 = s2 and Node 5 = s2. S12 indicates that the preventive measure, strengthening drainage facilities, is taken while the rescue is not, that is, Node 3 = s1 and Node 5 = s2. S13 indicates that only the rescue measure, draining floodwater and perform emergency repairs, is taken, that is, Node 3 = s2 and Node 5 = s1. S14 indicates both the precaution and rescue measures are taken, that is, Node 3 = s1 and Node 5 = s1. We analyze the consequences of construction sites damage, that is, the posterior probability of Node 6, that may result from these four scenarios for different rainstorm risk states, as shown in Fig. 7.
The probability of construction sites damage in S12, S13, and S14 are much lower than that in S11, which means that strengthening drainage facilities and draining floodwater and perform emergency repairs can effectively reduce the impact. When the rainstorm is at the blue/yellow level, the consequence of S12 is better than that of S13, while when the rainstorm is at the orange/red level, it is the opposite. That is, in order to reduce the damage of construction sites, precautions should be emphasized when the rainstorm level is low, and rescue measures should be emphasized when the rainstorm level is high.
-
(2)
Waterlogging of transportation infrastructure
We adjust the states of Node 8, Node 10, Node 12, and Node 14 and generate eight scenarios of waterlogging of transportation infrastructure, S21–S28. S21 indicates that no emergency response measure is taken. S22, S23, and S24 represent that some precautions are taken while rescue measure is not. S25, S26, and S27 represent that some rescue measures are taken while precaution is not. S28 indicates all precautions and rescue measures are taken. The consequences of these scenarios are shown in Fig. 8. Compared with the baseline scenario S21, the probability of casualties caused by waterlogging in S22–S24 is reduced, but not obvious, while that in S25–S27 is significantly reduced. It implies that preventive measures like dredging drainage lines and issuing traffic warnings can have some effects, however, due to the necessary travel needs like commuting, the traffic risk still exists, resulting in the risk of vehicle trapped and casualties. In these scenarios, rescue measures like draining floodwater and controlling traffic and rescuing trapped people in time should be enhanced in particular.
-
(3)
Houses flooded and collapsed
Seven scenarios, S31–S37, are generated for this disaster chain, by adjusting the states of Node 17, Node 19, Node 20, and Node 22. S31 indicates that no emergency response measure is taken. S32, S33, and S34 respectively represent that one kind of precaution is taken. S35 represents that the rescue measure is taken and S36 represents that all precautions are taken. S37 indicates that all precautions and rescue measures are taken. The consequences of these scenarios are shown in Fig. 9. The probability of casualties caused by house collapse in S32 and S33 is reduced compared with that in S31, which means precautions like eliminating hidden troubles, reinforcing houses, repairing houses, and removing stagnant water play a constructive role. Moreover, the probability of casualties in S34 is most significantly reduced. That is, evacuating and resettling people is the most effective measure to be implemented in house collapse scenarios.
-
(4)
Flooding
For flooding, there are three kinds of consequences: casualties, disrupted living, and inundation and damage of houses, farmland, roads, and bridges. We construct scenarios for each consequence and obtain 18 scenarios in total, as shown in Figs. 10, 11, and 12. Of the 7 scenarios in Fig. 10, S41 is the baseline scenario, that is, no emergency response measure is taken. S42, S43, S44, and S45 are each with one of the four emergency response measures taken: dredging and patrol, regulating flood and block crevasse, evacuating and resettling people, and timely rescue and treatment. S46 is with three precaution measures, and S47 is with all measures. By comparing the results of S42–S45, it can be seen that the probability of casualties in S45 is significantly reduced compared with the baseline scenario S41, followed by S44, S43, and finally S42. That is, timely rescue is the most effective measure to decrease flood-induced injury and death, followed by evacuating people. For disrupted living, the consequence in S412 is significantly lighter (see Fig. 11), which means that communicating with the affected residents is effective. The probability of house/farmland/road/bridge damage in S415 is reduced significantly (see Fig. 12), which implies that performing emergency repairs should be emphasized under this circumstance.
-
(5)
Geological disasters
There are two kinds of consequences of geological disasters: house/farmland/lifeline system damage and casualties. For each consequence, through adjusting the states of Node 41, Node 43, Node 46, and Node 48, 11 scenarios are generated, as shown in Figs. 13 and 14. When the rainstorm is at the blue/yellow level, the consequence of S52 and S56 is better than that of S53 and S57, while when the rainstorm is at the orange/red level, it is the opposite. That is, in order to reduce the damage of geological disasters, water content monitoring, slope displacement monitoring, patrol, and protection should be emphasized when the rainstorm level is low, and disaster investigation and management should be emphasized when the rainstorm level is high. Another noteworthy fact is that the probability of casualties in S59 does not decrease significantly as that in S58, which means that rescuing victims is not very effective. As rainstorm-induced geological disasters usually occur in remote areas, once people are trapped, it is difficult to rescue in time, so early warning and evacuation are more important.
-
(6)
Dam break
Generally, the probability of dam break events is very low. Here we assume that the rainstorm occurs in a mining area or tailings pond (Node 50 is set to s2). By adjusting the states of precaution nodes (Node 51 and Node 53) and rescue nodes (Node 54 and Node 56), eight scenarios (S61–S68) are obtained. The consequences of these scenarios are shown in Fig. 15. It can be seen that the probability of casualties in S62, S63, and S64 is reduced more significantly than in others. This shows that precautions like identifying hidden dangers, inspecting dredging and flood discharge facilities, monitoring, early warning, and transferring people in time should be implemented in dam break scenarios.
4.2 Result Analysis and Discussion
Through the scenario analysis, the following conclusions can be drawn.
-
(1)
In order to reduce casualties, it is very important to transfer people and carry out a rescue effort in time. For waterlogging, draining, controlling traffic, and rescuing in time should be implemented; For house collapse, geological disaster, and dam break, early warning and timely transfer of people are needed.
-
(2)
To reduce the damage of construction sites and infrastructures, when the rainstorm level is low, it is particularly important to strengthen preventive measures like regulating flood, eliminating hidden troubles, and reinforcing houses and pipelines; When the rainstorm level is high, rescue measures like performing emergency repairs are particularly important.
-
(3)
In order to reduce the impact on people’s living, it is necessary to communicate with the affected residents and take safety measures.
To further verify the validity of the method, we take five typical rainstorms as examples to compare the differences between the predicted and actual results, as shown in Fig. 16a. It can be concluded that the estimated results based on BN are basically consistent with the actual results, which proves that the proposed method is of great theoretical and practical significance for emergency management decision makers to grasp the overall situation of the rainstorm, identify the key nodes, and take emergency response measures in time. By regulating the response node status of the five storm disaster BN networks, it is analyzed that if all the emergency response measures are in place during each rainstorm response, there is some room for further reduction in the consequences and losses, as shown in Fig. 16b. For example, in response to Case 1, if all affected residents are transferred and timely rescue and treatment measures are taken, then the probability of casualties will be reduced from 15.5 to 1.12%; in response to Case 3, if all the drainage capacities are pre-positioned in place and water is pumped out in a timely manner, then the probability of waterlogging on roads will be reduced from 30.8 to 19.6%. Although these estimated values are not entirely accurate, they do indicate to some extent that the emergency response strategy can still be further optimized.
The scenario reasoning method proposed in this study can be used for strategy optimization in the rescue process of rainstorms as well as emergency drills. However, it still has limitations. In our constructed BN model, the discretization of parameter values is relatively simple, and only the presence or absence of most emergency response measures is considered, so only qualitative strategy suggestions can be given, which cannot be quantified. Besides, all the cases and experts in this study are from City B, leading to the limitation that our established BN model is only suitable for City B and some parameters may have to be adapted if applied to other cities.
5 Conclusion
The complexity and uncertainty of disaster chains bring about the difficulty of quickly making the most appropriate emergency decisions depending entirely on expert knowledge. To address this issue, a scenario-based decision approach is a good choice. In this study, we proposed a Bayesian network-based scenario reasoning method for disaster chains. The graphical nature of BN representation enables the interacting relationships among key factors to be easily understood by emergency decision makers, and it can capture the uncertainty of the model and provide an almost real-time scenario reasoning procedure. To overcome the bottleneck of BN parameter learning, we proposed the PEUK algorithm, which applies the maximum entropy principle to combine data learning and expert knowledge. Compared with the classical MAP algorithm and the direct expert opinion elicitation approach, our proposed PEUK approach performs the best in disaster consequence reasoning. Rainstorm events are taken as an example to show the process of model construction and scenario analysis. The results show that our approach with BN has important theoretical and practical significance for emergency decision makers to understand the overall situation of rainstorm disaster chains, identify key nodes, and take emergency response measures in time.
Further research can be carried out from two aspects. First, a disaster such as a rainstorm is unevenly distributed in time and space, which suggests that we can divide the administrative region into finer spatial grids, consider the evolution of disasters in different periods, and then carry out multi-objective dynamic decision making. Second, more disaster cases should be collected to modify the CPTs, so as to make the BN network more scientific and better guide practice.
References
Alexander, D. 2013. Emergency and disaster planning. In Disaster management: International lessons in risk reduction, response and recovery, ed. A. Lopez-Carresi, M. Fordham, B. Wisner, I. Kelman, and J.C. Gaillard, 125–141. London: Routledge.
Balbi, S., F. Villa, V. Mojtahed, K.T. Hegetschweiler, and C. Giupponi. 2016. A spatial Bayesian network model to assess the benefits of early warning for urban flood risk to people. Natural Hazards and Earth System Sciences 16(6): 1323–1337.
Berger, A., S. Della, and V. Della. 1996. A maximum entropy approach to natural language processing. Computational Linguistics 22(1): 39–71.
de Campos, C., and Q. Ji. 2008. Improving Bayesian network parameter learning using constraints. In Proceedings of the 19th International Conference on Pattern Recognition, 8–11 December 2008, Tampa, Florida, USA.
Chang, R., and W. Wang. 2010. Novel algorithm for Bayesian network parameter learning with informative prior constraints. In Proceedings of the 2010 International Joint Conference on Neural Networks, 18–23 July 2010, Barcelona, Spain.
Chen, S., and C. Pollino. 2012. Good practice in Bayesian network modelling. Environmental Modelling & Software 37: 134–145.
Comes, T., M. Hiete, N. Wijngaards, and F. Schultmann. 2011. Decision maps: A framework for multi-criteria decision support under severe uncertainty. Decision Support Systems 52(1): 108–118.
Comes, T., N. Wijngaards, and B. Van de Walle. 2015. Exploring the future: Runtime scenario selection for complex and time-bound decisions. Technological Forecasting and Social Change 97: 29–46.
Fan, W.C., Y. Liu, W.G. Weng, and S.F. Shen. 2013. An introduction to public safety science. Beijing: Science Press (in Chinese).
Han, L.N., J.Q. Zhang, Y.C. Zhang, Q. Ma, S. Alu, and Q.L. Lang. 2019. Hazard assessment of earthquake disaster chains based on a Bayesian network model and ArcGIS. ISPRS International Journal of Geo-Information 8(5): Article 210.
Hosseini, S., and D. Ivanov. 2020. Bayesian networks for supply chain risk, resilience and ripple effect analysis: A literature review. Expert Systems with Applications 161: Article 113649.
Hou, Y.Y., E.R. Zheng, W.Q. Guo, Q.K. Xiao, and Z.W. Xu. 2020. Learning Bayesian network parameters with small data set: A parameter extension under constraints method. IEEE Access 8: 24979–24989.
Koller, D., and N. Friedman. 2009. Probabilistic graphical models: Principles and techniques. Cambridge, MA: MIT Press.
Liu, Z.Q., F. Nadim, B. Vangelsten, U. Eidsvig, and B. Kalsnes. 2014. Quantitative multi-risk modelling and management using Bayesian networks. In Landslide science for a safer geoenvironment, ed. K. Sassa, P. Canuti, and Y. Yin, 773–779. Cham: Springer.
Liu, C., J. Qian, D.H. Guo, and Y. Liu. 2018. A spatio-temporal scenario model for emergency decision. GeoInformatica 22(2): 411–433.
Moehrle, S., and W. Raskob. 2015. Structuring and reusing knowledge from historical events for supporting nuclear emergency and remediation management. Engineering Applications of Artificial Intelligence 46: 303–311.
Niculescu, R., T. Mitchell, and R. Rao. 2006. Bayesian network learning with parameter constraints. Journal of Machine Learning Research 7: 1357–1383.
Qiu, J.N., Z.Q. Wang, X. Ye, L.L. Liu, and L.L. Dong. 2014. Modeling method of cascading crisis events based on merging Bayesian network. Decision Support Systems 62: 94–105.
Rohmer, J. 2020. Uncertainties in conditional probability tables of discrete Bayesian belief networks: A comprehensive review. Engineering Applications of Artificial Intelligence 88: Article 103384.
Sakahira, F., and U. Hiroi. 2021. Designing cascading disaster networks by means of natural language processing. International Journal of Disaster Risk Reduction 66: Article 102623.
Shi, P.J. 1996. Theory and practice of disaster study. Journal of Natural Disasters 5(4): 6–17 (in Chinese).
Wu, C.G., X. Xu, B.K. Zhang, and Y.L. Na. 2013. Domain ontology for scenario-based hazard evaluation. Safety Science 60: 21–34.
Yu, F., B. Fan, and X.Y. Li. 2020. Improving emergency preparedness to cascading disasters: A case-driven risk ontology modelling. Journal of Contingencies and Crisis Management 28(3): 194–214.
Yu, F., B. Fan, C.S. Qin, and Y. Chen. 2023. A scenario-driven fault-control decision support model for disaster preparedness using case-based reasoning. Natural Hazards Review. https://doi.org/10.1061/NHREFO.NHENG-1722.
Zadeh, L.A. 1965. Fuzzy sets. Information and Control 8(3): 338–353.
Zhang, H., and Y. Liu. 2012. Key problems on fundamental science and technology integration in “scenario-response” based national emergency response platform system. System Engineering – Theory & Practice 32(5): 947–953 (in Chinese).
Zhong, S.B., Z.X. Fang, M. Zhu, and Q.Y. Huang. 2017. A geo-ontology-based approach to decision-making in emergency management of meteorological disasters. Natural Hazards 89(2): 531–554.
Zhou, Y., N. Fenton, and C. Zhu. 2016. An empirical study of Bayesian network parameter learning with monotonic influence constraints. Decision Support Systems 87: 69–79.
Acknowledgments
This work was supported by the National Key Research and Development Program of China (Grant No. 2021YFF0600400) and the National Natural Science Foundation of China (Grant Nos. 72104123, 72004113).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Huang, L., Chen, T., Deng, Q. et al. Reasoning Disaster Chains with Bayesian Network Estimated Under Expert Prior Knowledge. Int J Disaster Risk Sci 14, 1011–1028 (2023). https://doi.org/10.1007/s13753-023-00530-w
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13753-023-00530-w