Introduction

Groundwater is a vital resource for human survival and the environment. It provides drinking water to millions of people, supports agriculture, industry, and sustains ecosystems. However, exploitation and contamination threaten this precious resource. It is mandatory to protect and manage groundwater to ensure its availability for future generations (Babu et al. 2015). Groundwater gets contaminated by anthropogenic and geogenic activities. Anthropogenic activities such as application of fertilizers and industrial discharges contaminate groundwater to a large extent. However, geogenic contaminants such as arsenic, fluoride, and radon can enter into groundwater through natural processes such as weathering of rocks and minerals. Fluoride possesses a greater impact than any other contaminants. The fluoride contaminant is often found in high concentrations in certain regions of the world, particularly in developing countries such as India, China, and Pakistan (Rasool et al. 2015; Chen et al. 2017; Jha and Tripathi 2021). The consequences of consuming fluoride-contaminated groundwater were found to be severe. Fluoride toxicity can lead to dental fluorosis and skeletal fluorosis. Preventing geogenic contamination requires a multi-faceted approach that includes identifying areas with high levels of fluoride contamination, monitoring the fluoride migration and implementing appropriate in situ treatment technologies for affected groundwater sources (Ayoob and Gupta 2006; Hug et al. 2020). Numerical modeling aids in predicting, managing, and recommending remedial measures for groundwater pollution. MODFLOW effectively replicates groundwater flow and transport processes. Groundwater models use numerical equations to describe water flow and contaminants transport, based on simplifying assumptions such as flow direction, aquifer formation, and heterogeneity of bedrock (Koda 2012; Surinaidu et al. 2014; Sundararaj et al. 2022; Madhavan et al. 2023).

Visual MODFLOW has become an essential tool for hydrologists and geologists working in the field of groundwater modeling. Its ease of use, flexibility and powerful analytical capabilities have made it an indispensable part of many research projects around the world. Researchers from a wide range of disciplines have utilized MODFLOW to predict the movement of contaminants in groundwater under a variety of hydrogeological situations (Panagopoulos 2012; Jabeen et al. 2019; Banaei et al. 2021; Sundararaj et al. 2022). Visual MODFLOW was used to predict groundwater levels, groundwater flow in hard rock aquifer systems and further it limits of data and numerical techniques from mathematical models (Varalakshmi et al. 2014; Jabeen et al. 2019; Prabhu and Inayathulla 2019; Chakraborty et al. 2020). Excessive groundwater extraction without augmentation depletes groundwater resources. Groundwater flow modeling provides a method for improving the recharge system wherever it is required (Chitsazan and Movahedian 2015; Saleem et al. 2018; Siva Prasad et al. 2021). Khadri and Pande (2016) designed sustainable groundwater resource management using Visual Modular Three-Dimensional Flow-20011 code supported by groundwater modeling software (GMS). Recharge, extraction, return flow, and soil coverage were all modelled as part of the source/sink coverage. The model’s simulation result suggests good precautionary measures. The visual MODFLOW and MT3DMS tools are used at industrial pollution sites to forecast groundwater flow and chromium migration from tanneries (Rao et al. 2011). Additionally, the geographical migration of chromium, ammonium, chloride, arsenic, and fluoride in groundwater was also investigated using MT3DMS (Jabeen et al. 2019; Guo et al. 2021). The process of simulating the migration of iron and heavy metals through MODFLOW reveals that the total dissolved solids (TDS) concentration increases as a result of the rapid movement of those elements (Bougherira et al. 2014; Durgaprasad et al. 2017). In addition, research was conducted to determine the migration of orthophosphate and fluoride ions along the groundwater flow direction utilizing visual MODFLOW (Melki et al. 2020a, b). Furthermore, multi-criteria decision-making (MCDM) was used to determine a suitable location for the disposal of municipal solid waste (Saranya et al. 2016). Continuous discharge of textile industry effluents without any treatment is more hazardous to groundwater (Saravanan et al. 2011; Arumugam et al. 2020). As a result, the demarcation of groundwater protection zones and wells is monitored to identify the harmful pollutants in the groundwater. Due to leaching of ore minerals from waste rock heaps and mining operations are boosting manganese migration into groundwater (Shang et al. 2019; Xie et al. 2021). Visual MODFLOW and MT3D were used to develop a groundwater flow model for the river sub-basin (Babu et al. 2015; Maheswaran et al. 2016; Vallner and Porman 2016; Chakraborty et al. 2020; Siva Prasad et al. 2021). The model suggests optimum utilization of groundwater for a micro-irrigation system that protects groundwater from contamination. In addition to it, saline water intrusion affects aquifers towards inland. Better management requires groundwater protection zone demarcation. Active and abandoned contaminated sites and phosphogypsum leachate collect basins on the seashore pollute groundwater. A numerical modeling simulating the site performed using MT3DMS reveals high concentration of fluoride in the saturated zone (Melki et al. 2020b).

Earlier research on fluoride contamination in groundwater in peninsular India has focused more on the origins, occurrence of fluoride, geochemical process of fluoride migration, hydrogeochemistry and spatial distribution of fluoride using IDW interpolation methods (Sajil Kumar et al. 2014; Nagaraj and Masilamani 2023). However, only a few studies were carried out using MODFLOW to investigate fluoride migration in groundwater from dump sites (Melki et al. 2020b). These investigations are limited in their ability to detect fluoride diffusion from nonpoint sources. Vaniyambadi and Ambur taluks, located in Tirupathur district, have hard rock geology made up of charnockite and granite-gneiss, which often leads to elevated fluoride levels in groundwater due to natural leaching from fluoride-bearing minerals (Kom et al. 2023; Shaji et al. 2024). So it is essential to monitor fluoride transport to suggest mitigation measures. Hence, the main objective of this work focuses on identifying fluoride-affected zones and fluoride migration from nonpoint fluoride sources using Visual MODFLOW flex. In addition to this, Human Health Risk Assessment (HHRA) has also been determined to identify the sample location affected by fluoride pollution.

Study area

General

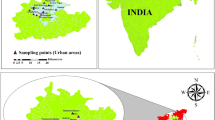
The study area Vaniyambadi and Ambur taluks were located in Tirupathur district of Tamil Nadu, India. It has an extended area of about 978.41 Sq.km situated between 12° 26′ 54.52"N to 12° 54′ 39.23"N latitude and 78° 28′ 9.56"E to 78° 55′ 0.75"E longitude, as shown in Fig. 1. It has the highest elevation of 697 m and minimum of 279 m from mean sea level. The climatic condition in the study region is warm in May and cold in August. The highest temperature recorded 36.5 °C and the lowest is 10.2 °C. Vaniyambadi and Ambur taluks receive 1892 mm and 665 mm of annual rainfall, respectively. Groundwater is recharged by the Palar River, which flows in the eastward direction in Ambur taluk.

Fig. 1
figure 1

Study area map of Vaniyambadi and Ambur taluks

Full size image

Land use land cover

Figure S1 depicts a land-use land-cover (LULC) map of the study area. Agriculture and forest land combined with grassland occupy 77.19% of the study area. A human habitant occupies build-up land at an average density of around 11.49%, with the most residents in the central part of Vaniyambadi and Ambur taluks. Furthermore, the research area has 10.07% barren land as it is located in hard rock-hilly terrain. Water bodies occupy 1.25% of the study area, which includes Palar River basin, lakes, ponds, etc.

Geology

The geological group of the study region was established based on geology and mineral maps available from the Geological Survey of India, as shown in Fig. 2. The southern half of the Palar River Basin is dominated by the Charnockite group of rocks, while the northern part is dominated by Fissile Hornblende Gneiss and Granitoid Gneiss. The alkaline forms of rock around the Yelagiri hill region are a complex combination of syenite and epitode hornblende gneiss. The yelagiri syenite complex was emplaced into charnockite and granite gneiss. The study region was divided into two provinces based on geological characteristics such as alluvium and charnockite, which has high and low permeability, respectively.

Fig. 2
figure 2

Geology map of Vaniyambadi and Ambur taluks

Full size image

Methodology

The methodology section of this study consists of the following phases: data collection, thematic map creation for a conceptual model, assigning aquifer properties, assigning boundary conditions and simulating the model for the flow of groundwater and the transport of contaminants. Figure 3 depicts the methodology flow chart of this study. In addition, health risk assessment of 40 sampling wells was also determined.

Fig. 3
figure 3

Methodology flow of this study

Full size image

Data collection

Aquifer properties such as hydraulic conductivity, transmissibility, specific yield, specific storage and porosity were collected from the Central Ground Water Board (CGWB). Lithology, water level, and rainfall data for the study area are collected from State Ground and Surface Water Resources Data Centre. Elevation of the study area was obtained through Inverse Distance Weighted (IDW) interpolation technique using Quantum Geographic Information System (QGIS). Elevation of the sampling well was also verified using Global Positioning System (GPS).

Numerical model of groundwater flow and contaminant transport

Numerical modeling of groundwater flow confined and unconfined aquifer represents the three-dimensional mathematical Eqs. (1) and (2), respectively, which is used to simulate the groundwater flow using MODFLOW in the study area (Saravanan et al. 2010).

$$\frac{\partial }{{\partial {\text{x}}}}\left( {{\text{K}}_{{\text{x}}} \frac{{\partial {\text{h}}}}{{\partial {\text{x}}}}} \right) + \frac{\partial }{{\partial {\text{y}}}}\left( {{\text{K}}_{{\text{y}}} \frac{{\partial {\text{h}}}}{{\partial {\text{y}}}}} \right) + \frac{\partial }{{\partial {\text{z}}}}\left( {{\text{K}}_{{\text{z}}} \frac{{\partial {\text{h}}}}{{\partial {\text{z}}}}} \right) = {\text{S}}_{{\text{s}}} \frac{{\partial {\text{h}}}}{{\partial {\text{t}}}} - W$$
(1)
$$\frac{\partial }{{\partial {\text{x}}}}\left( {{\text{K}}_{{\text{x}}} {\text{h}}\frac{{\partial {\text{h}}}}{{\partial {\text{x}}}}} \right) + \frac{\partial }{{\partial {\text{y}}}}\left( {{\text{K}}_{{\text{y}}} {\text{h}}\frac{{\partial {\text{h}}}}{{\partial {\text{y}}}}} \right) + \frac{\partial }{{\partial {\text{z}}}}\left( {{\text{K}}_{{\text{z}}} {\text{h}}\frac{{\partial {\text{h}}}}{{\partial {\text{z}}}}} \right) = {\text{S}}_{{\text{y}}} \frac{{\partial {\text{h}}}}{{\partial {\text{t}}}} - W$$
(2)

where \({\text{K}}_{\text{x}}\), \({\text{K}}_{\text{y}}\) and \({\text{K}}_{\text{z}}\) are hydraulic conductivity along with x, y and z directions (LT−1); h—hydraulic head (L); \(\text{W}\)—volumetric flux per unit volume represents the sources/sinks (T−1); \({\text{S}}_{\text{s}}\)—specific storage (L−1); t—time (T).

Solute transport in MT3D is described by Eq. (3) for contaminant transport through porous media (Saravanan et al. 2010; Saba et al. 2016). This equation represents the movement of a solute in groundwater using advection, dispersion, and possible additional processes such as chemical reactions and sorption. The equation for fluoride transport specifically takes into account the advection of fluoride with groundwater flow, its spread due to varying velocity (dispersion), and additional fluoride transport processes, such as sorption or complexation reactions. MT3D numerically solves this equation to simulate fluoride migration and distribution throughout the aquifer system.

$$\frac{\partial }{\partial {x}_{i}}\left({D}_{ij}\frac{\partial c}{\partial {x}_{j}}\right)-\frac{\partial }{\partial {x}_{i}}\left({v}_{i}c\right)+ \frac{{q}_{s}}{n}{C}_{s}\pm R=\frac{\partial c}{\partial t}$$
(3)

where \({D}_{ij}\)—dispersion coefficient (L2T); c—concentration of solute (ML−3); \({v}_{i}\)—groundwater velocity (LT−1) (Specified flex volume in porous media, i.e. \({v}_{i}=\frac{{q}_{i}}{\text{n}}\)); \({\text{q}}_{\text{s}}\)—volumetric flow of water per unit volume of an aquifer indicates sources (positive) and sinks (negative); n—porosity of porous medium; \({\text{C}}_{\text{s}}\)–concentration of sources/sinks (ML−3); R—rate of sources/sinks for chemical reaction.

Thematic map creation for a conceptual model

A base boundary map was created in QGIS. Surfer v.9 was used for developing three surface layers based on lithology (bore log data) using the kriging interpolation technique. The top layer is assigned as erosional (unconfined), whereas the other two are deformed (confined). Using boundary and surface maps, the conceptual model is shown in Fig. 4a, which was created using Visual MODFLOW Flex 6.1. This model has been converted into a numerical model. The finite difference grid was created for a three-layer groundwater model with a total study area of 955 km2, with each grid cell sized 1000 m × 1000 m (51 rows × 49 columns). The grid formation of the study area is shown in Fig. 4b.

Fig. 4
figure 4

a Conceptual model of the study area. b Grid formation of the study area

Full size image

Assigning aquifer properties

Aquifer properties collected from CGWB has been used in this study for groundwater flow modeling. According to District Groundwater Brochure for Vellore district and Aquifer Disposition & Aquifer Management Plan published by Aquifer Information Management System (CGWB 2009), aquifer was designated into three layers: first layer consists of alluvium (topsoil) with a thickness of 2.5 m; second layer and third layer have thicknesses of 17.5 m and 180 m, respectively, and it consists of weathered gneiss-charnockite and fractured gneiss-charnockite. Hydraulic conductivity for layer 1, layer 2, and layer 3 varies from 3.5 × 10−5 m/s to 3.8 × 10−4 m/s, 2.6 × 10−6 m/s to 3.9 × 10−5 m/s, and 2.6 × 10−7 m/s to 3.4 × 10−5 m/s, respectively. The average for three layers value for the study area is 2 × 10−4 m/s, 1.2 × 10−5 m/s, and 8.7 × 10−5 m/s, which was considered. The model was performed by assuming horizontal conductivity (Kx = Ky) and vertical conductivity (Kz) taken as 0.1 times of Kx. The three-layer aquifer system of study is shown in Fig. 5. Table 1 shows the key parameter ranges considered for the modeling. Table 2 shows the aquifer characteristics and hydrogeological characteristics such as specific storage (Ss), specific yield (Sy), effective porosity (ne), total porosity (n), rainfall, and recharge that were all assigned for groundwater flow modeling.

Fig. 5
figure 5

Three-layer aquifer system of the study area

Full size image
Table 1 Key parameter ranges used for groundwater modeling
Full size table
Table 2 Aquifer and hydrogeological characteristics of the study area for groundwater modeling
Full size table

Assigning boundary conditions

Recharge (RCH) and well packages (WEL) were taken as boundary conditions under the specified flux and river (RIV) package with head-dependent variable with consideration for groundwater inflow and outflow. The RCH contains the entire water entering into an aquifer, the WEL represents the total discharge of pumping well water from an aquifer, and the RIV includes the amount of infiltration of water from the river. The rainfall precipitation data were obtained from Indian Meteorological Department (IMD) and India Water Resources Information System (India-WRIS). The total amount of rainfall in the study area was found to be 1000 mm/year. 20% of the total rainfall was considered as recharge in this study area. A total of 40 numbers of pumping wells are considered in this study. For domestic and agricultural purposes, groundwater is withdrawn from these wells. Pumping is considered 8 h per day during the non-monsoon season and 4 h per day during the monsoon season. As a result, an average of 6 h per day has been considered for this model. During pumping tests, the pumping rates or discharge rates (Q) of pumping wells are calculated by collecting the amount of water pumped in litres per second (lps). The average pumping period for each well considered to be 6 h/day is given as input for the model. Hence, it has been assigned to a minimum of 2 m3/day and a maximum of 189 m3/day. Figure 6 illustrates the location of pumping wells and river boundaries.

Fig. 6
figure 6

Location of pumping wells and river boundaries

Full size image

Simulation of groundwater flow and contaminant transport

The simulation of groundwater flow in unconfined and weathered part of confined aquifer systems was performed in MODFLOW 2005 WH using Visual MODFLOW v6.1 on monthly time step periods, whereas a mass transport simulation was performed for plume migration of fluoride contamination using modular three-dimensional transport model (MT3D).

Model calibration is performed to modify and match the input parameters to the observed head and fluoride concentration. Changes were made to the model input parameters until the simulation results are correlated with the observed data. The necessity for model calibration arises from uncertainty parameter values due to assumptions in conceptual models. Before using a model for forecasts or decision validation, calibration has been carried out to promote the suitability of groundwater behaviour. The key parameters have been fine-tuned in MODFLOW are aquifer characteristics, hydraulic conductivity, boundary conditions such as pumping well, river, recharge to create a good match with the observed hydraulic head and flow rate measurements at the outlet streams.

As per the methodology followed by Saravanan et al. (2010); Siva Prasad et al. (2021); Sundararaj et al. (2022), model has been calibrated for both steady and transient states. In steady-state model calibration, the water levels in May 2021 are taken as the initial heads of the study area, which are shown in Table S1. The calibration process involved varying the hydraulic conductivity within specific ranges until the monitored water levels matched the simulated ones. Subsequently, transient calibration was performed for the period from May 2021 to April 2022, with a time step frequency of 30 days. The calibration values for water levels, hydraulic conductivity, and boundary conditions obtained under steady-state conditions were used as the initial inputs for the transient model calibration.

The modular three-dimensional transport model (MT3D) was used to evaluate the effect of fluoride pollution from fluoride-enrich hard rock in groundwater. It was expected that geogenic contamination of fluoride would remain as a continuous source of pollution. As a result, the transient simulation employed identical conditions for specific yield, specific storage, pumping rates, and recharge.

Validation of the model is an extension of calibration that ensures the model calibrated accurately evaluates all the factors that potentially affect simulation outcomes. To validate a model, the most effective method is to utilize a subset of the data observed for calibration. After obtaining the value of the final results through calibration, the remaining observed data period is maintained for validation. Therefore, observed data from field investigation in May 2023 are described in Tables S2 and S3, and these data were used to evaluate the model for goodness of fit.

Human Health Risk Assessment (HHRA)

HHRA is used to evaluate the human health impact of water quality parameters on adults and children. Pollutants enter the human body via three different routes: ingestion, dermal adsorption and inhalation. Of which ingestion and dermal entry are the most probable ways for water contaminants to reach the human body, these two methods of mechanisms are investigated in this study (Qasemi et al. 2023). Equations 4–8 are used to compute the daily exposure dosage of ingestion and dermal adsorption.

$${\text{ADD}}_{\text{ingestion}}= \frac{{\text{C}}_{\text{w}}*\text{IR}*\text{EF}*\text{ED}}{\text{BW}*\text{AT}}$$
(4)
$${\text{ADD}}_{\text{dermal}}= \frac{{\text{C}}_{\text{w}}*\text{SA}*{\text{K}}_{\text{p}}*\text{ET}*\text{EF}*\text{ED}*{10}^{-3}}{\text{BW}*\text{AT}}$$
(5)
$${\text{HQ}}_{\text{ingestion}}= \frac{{\text{ADD}}_{\text{ingestion}}}{\text{Rfd}}$$
(6)
$${\text{HQ}}_{\text{dermal}}= \frac{{\text{ADD}}_{\text{dermal}}}{\text{RfD}}$$
(7)
$$\text{Hazard Index }\left(\text{HI}\right)={\text{HQ}}_{\text{ingestion}}+ {\text{HQ}}_{\text{dermal}}$$
(8)

where ADDingestion and ADDdermal are the average daily exposure doses of water from ingestion and dermal adsorption (mg/kg/day); these are estimates average daily dose of a contaminant consumed through ingestion and absorbed through dermal contact, respectively. HQingestion and HQdermal are the Hazard Quotient of ingestion and dermal, assess the non-carcinogenic risk for these exposure pathways, where values exceeding 1 indicate significant health concerns. HI is the hazard index, which combines risks from multiple pathways to determine the overall non-carcinogenic risk, Cw is the average concentration of the water quality parameters (mg/L), IR is ingestion rate (L/day), EF is exposure frequency (day/year), ED is the exposure duration (years), BW is the average body weight (kg), AT is the average time (days), SA is the average surface area of the skin exposed to water (cm2), Kp is the coefficient of the water for dermal activity (0.001 for Na2+, F−, NO3− and Cl−), SA and Kp influence the estimation of dermal absorption rates. ET is the exposure time (hrs/day); RfD is the reference dose of the water quality parameters (mg/kg/day) (F− = 0.06 and NO3− = 1.6) and provides a safety threshold for daily contaminant intake without adverse effects (USEPA 2014; Subba Rao et al. 2020; Iqbal et al. 2023). Table S4 summarizes the standard values utilized in the HHRA calculation.

Result and discussion

Modelling of groundwater flow and contaminant transport

The groundwater flow model and fluoride transport model were calibrated using field water level data and fluoride concentrations from 2021 to 2022, and the model was validated using field water level and fluoride concentration data from 2023, as described in Tables S2 and S3, respectively. The groundwater flow head and fluoride concentration are predicted for 2041. In this study, calibration criteria such as standard error of the estimate (SEE), root mean square (RMS), root-mean-square error (RMSE), and normalized root-mean-square error (NRMSE) were considered for evaluation.

Calibration of groundwater head

The water level data collected in May 2021, which is shown in Table S1, were used as the initial head in the model simulation for heads for April 2022. The water-level deviations of wells were observed maximum of 716.5 m and a minimum of 276.15 m. The water level contour map of April 2022 is shown in Fig. 7; it was observed that water level in the hilly areas was at a higher elevation compared to water level in the wells along the vicinity of the river basin though it gets replenishment from the basin. The model input period was set to May 2021, and the simulation was run for a year at 30-day intervals to calibrate for May 2022. The observed heads for each well were compared to the calculated heads from this model calibration, as shown in Table 3.

Fig. 7
figure 7

Water level contour map for the year 2022

Full size image
Table 3 Comparison of the observed and calculated head for the year 2022 and predicted head for the year 2041
Full size table

The comparison of observed and computed heads of 40 wells over the calibration period is shown in Fig. 8, indicating a positive strong correlation between observed and simulated well heads and model sustainability. Furthermore, the R2 value was found to be 0.98, which was closer to 1, since the observed and calculated water-level elevations were nearly identical. The results for the SEE, RMSE and NRMSE were 3.72 m, 27.87 m and 6.33%, respectively.

Fig. 8
figure 8

Comparison of observed and calculated head for the year 2022

Full size image

The water-level elevations calculated from steady-state simulation were established as the initial head for transient state calibration. Hydrogeological characteristics of the aquifer and water level obtained by steady-state simulation are given as initial conditions of transient state model calibration. The transient state model calibration was performed for periods of 2021 to 2022. Recharge estimated according to Groundwater Estimation Committee (GEC) criteria in the study area is used as input for transient model calibration. The rainfall of every year converted as recharge of 20%, and 30% for the years 2021, 2022 respectively. The transient state model was calibrated with the comparison of observed and calculated water levels for a period of 365 days to 7305 days, as shown in Table 3.

Prediction of groundwater head

This calibrated model predicted for groundwater availability in 2041 after successful calibration. The calibrated model indicated the variation of groundwater heads in 2041, which would vary between 284.77 and 667.63 m above mean sea level (AMSL). For different years, the model output results, such as a spatial variation map of groundwater level and water budget charts, are obtained. In addition, Table 3 shows the comparison between heads of wells in 2022 and 2041. Figure 9 depicts a predicted groundwater contour map for 2041, whereas Fig. S2 shows a time-series graph of observed and calculated groundwater elevation for period of 365 days. According to the Tirupathur district's groundwater resource assessment, Alangayam and Vellakuttai regions in Vaniyambadi taluk are overexploited. The prediction indicates that if present conditions continue, the region will face severe water scarcity in the future.

Fig. 9
figure 9

Predicted groundwater head for the year 2041

Full size image

Groundwater budget and flow

Groundwater budget was estimated for the study region with a mass balance and output reports that were generated at the end of the groundwater model simulation. Figure S3 depicts the mass balance for 2041. This shows the input and output volume of water in cubic metres (m3) for different categories such as storage, wells, river leakage and recharge. The volume of recharge depicted in the graph was inadequate to meet the draught by the wells, indicating that additional water had been extracted from the aquifer, which could be met by the groundwater storage potential. Over 20-year time period, groundwater withdrawal was reduced from 12.2 × 106 to 0.69 × 106 m3. Hence, the groundwater budget over the next 20 years (from 2021 to 2041) shows a decrease in groundwater storage from 2.37 × 109 to 1.05 × 109 m3. According to the prediction analysis, the study area is expected to greatly struggle with groundwater shortages in 2041 in hilly regions and groundwater increases near the Palar River basin due to recharge.

The simulation result shows the groundwater flow direction towards the Palar River, which flows south to north in the centre of the study area. The groundwater flow direction for the years 2022 and 2041 is shown in Fig. 10. The magnitude of the groundwater flow velocity is directly proportional to the arrow size; the hilly region has a lower velocity compared to the velocity of flow near the river basin. This indicates the recharge is more in the wells that fall near the river basin.

Fig. 10
figure 10

Groundwater flow direction for the years 2022 and 2041

Full size image

Calibration of fluoride transport

In the simulation of the contaminant transport model, MT3D results were calibrated with the observed data in the field analysis for the year 2022. The initial concentration of 40 wells is shown in Table S1. The model was run from May 2021 to April 2022 with a time interval of 30 days. The comparison of calculated and observed fluoride concentrations of 40 wells shown in Fig. 11 reveals the strong correlation between simulated and observed fluoride concentration and the model’s sustainability. The value of R2 was 0.97, which was closer to 1 since the observed and calculated fluoride concentrations were nearly identical. The results for the RMSE and NRMSE were 0.23 m and 7.41%, respectively. Table 4 shows the observed and calculated values of fluoride concentration for 40 wells. The calculated fluoride concentration ranges between 0.3 mg/L and 3.49 mg/L.

Fig. 11
figure 11

Comparison of calculated and observed fluoride concentration for the year 2022

Full size image
Table 4 Comparison of observed and calculated fluoride concentration for the year 2022 and predicted fluoride concentration for the year 2041
Full size table

Prediction of fluoride transport

After the successful completion of the calibration model, the same was used for the prediction of fluoride concentration for the year 2041. The predicted fluoride concentration was found to the range between 0.35 and 2.69 mg/L. Spatial distribution of fluoride concentration at 365 days and predicted fluoride concentrations at 7305 days is shown in Fig. 12a and b, respectively. The observed and calculated fluoride concentration values for the year 2022 and predicted values for the year 2041 are shown in Table 4. Plume diffusion of fluoride contamination in the study area on the initial day, after 2 years and 20 years, is shown in Fig. 13a, b and c, respectively. The main geogenic source of fluoride contamination is charnockite and granite-gneiss complex rock in Yelagiri Hill, which has 4 mg/L. After 20 years of simulation, the fluoride concentration of the source point will be 9.91 mg/L and the plume will be extended up to 8 km towards the Palar River basin. The results of Figs. 12 and 13 reveal that fluoride contamination migrates towards the Palar River through groundwater flow. Initially, the fluoride content is greater in the Vellakuttai and Alangayam zones. After 20 years of simulation, Peddur, Reddiyur, Vellakuttai, Vijilapuram, Chengilikuppam, Chinna veppampattu, Kalendira, and Marapattu will be polluted by fluoride migration from the source of the Yelagiri Hill syenite complex (charnockite and granite gneiss). Furthermore, the Palar River in the Vaniyambadi area will be impacted by fluoride pollution migration after 20 years.

Fig. 12
figure 12

a Spatial distribution of fluoride concentration on 365 days. b Spatial distribution of predicted fluoride concentration on 7305 days

Full size image
Fig. 13
figure 13

a Plume diffusion of fluoride concentration on 1 day. b Plume diffusion of fluoride concentration on 730 days (2 years). c Plume diffusion of predicted fluoride concentration on 7305 days (20 years)

Full size image

Human Health Risk Assessment (HHRA) of fluoride contaminant

The average daily exposure dosage by ingestion (ADDing) and dermal adsorption (ADDder), as well as the Hazard Quotient of ingestion (HQing) and dermal (HQder), was calculated for adults and children. The Human Health Risk Assessment (HHRA) of fluoride for adults and children is summarized in Table 5. The ADDing values of fluoride for adults varied from 0.01 to 0.08 mg/kg/day with an average of 0.04 mg/kg/day and for children 0.01 to 0.15 mg/kg/day with an average of 0.07 mg/kg/day. Similarly, ADDder values of fluoride for adults varied from 0.0001 to 0.0004 mg/kg/day with an average of 0.0002 mg/kg/day and for children 0.0001 to 0.0012 mg/kg/day with an average of 0.0006 mg/kg/day. The Hazard Index (HI) values of fluoride for adults varied from 0.12 to 1.34 (Average = 0.68) and for children 0.21 to 2.44 (Average = 1.25).

Table 5 Fluoride’s Human Health Risk Assessment (HHRA) for adults and children
Full size table

Based on the calculations, it is clear that the HI values for children from all locations are greater than for adults due to the difference in body weight between adults and children. Figure 14 illustrates the Hazard Index (HI) values of adults and children for sampling locations. According to the HHRA, children are more severely affected than adults, because the HI values for children exceeded 1 in most of the sample locations. 62.5% of sampling locations have a health impact on children and 25% on adults due to fluoride contamination. Adult HI values exceed 1 in Peddur, Reddiyur, Vellakuttai, Vijilapuram, Chengilikuppam, Chinna veppampattu, Kalendira and Marapattu, indicating the severe impact of fluoride on human health due to geogenic contamination by fluoride transport in groundwater. Except at these sites, all other locations have HI values lesser than 1, indicating that fluoride has no impact of human health effect on adults and children at the locations.

Fig. 14
figure 14

Adult and children Hazard Index (HI) values for sampling locations

Full size image

Conclusion

The MODFLOW simulation reveals the groundwater flows towards the Palar River basin and other natural drains. Calibration of groundwater flow simulation results after 365 days indicates R2 value was 0.98, which was closer to 1, since the observed and calculated water level elevations were nearly identical. The results for the SEE, RMSE and NRMSE were 3.72 m, 27.87 m and 6.33%, respectively. The prediction model after 20 years indicates the variation of groundwater heads in 2041, which would vary between 284.77 and 667.63 m above mean sea level (AMSL).

The MT3D simulation reveals that the value of R2 was 0.97, which was closer to 1 since the observed and calculated fluoride concentrations were nearly identical. The results for the RMSE and NRMSE were 0.23 m and 7.41%, respectively. The calculated fluoride concentration ranges between 0.3 mg/L and 3.49 mg/L. The prediction of fluoride contamination after 20 years manifests most of locations polluted by fluoride migration from the source of the Yelagiri Hill syenite complex (charnockite and granite gneiss). The predicted fluoride concentration varies between 0.35 and 2.69 mg/L and source point will be 9.91 mg/L and the plume will be extended up to 8 km towards the Palar River basin. Furthermore, the Palar River in the Vaniyambadi area will be affected severely by fluoride pollution migration.

HHRA is used to evaluate the human health impact of water quality parameters on adults and children in the study area. According to the HHRA, children are more seriously affected than adults since their HI values exceed 1 in most of the study locations suggesting serious health effects from geogenic fluoride transport in groundwater. The study reveals that 62.5% of children and 25% of adults were affected by fluoride pollution.

Hence, this study is very useful to predict groundwater levels and fluoride migration in groundwater. Furthermore, HHRA evaluation is used to identify fluoride exposure in children and adults. The results from this study suggest various precautionary measures such as vertical barriers, impermeable reactive barriers, and cutoff walls that need to be deployed to prevent fluoride migration. This study has not employed geophysical techniques to determine the lithological characteristics. Further, this research can be enhanced by utilizing geophysical investigation to understand the impact of contaminant migration, and additionally, the fate and pollutant transport due to geogenic and anthropogenic activities can be explored.