Abstract
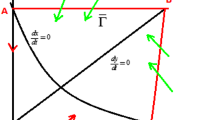
This paper proposes a single species system under seasonal succession and impulsive perturbations. The system is composed of two processes: one governed by the Gompertz equation, and the other modelled by the Logistic equation. The two processes are connected by impulse perturbations. Some very general, weak criteria on the permanence, existence, uniqueness and global stability of the positive periodic solution are established by analysis approaches based on the theory of discrete dynamical systems. The theoretical results are demonstrated by special examples and numerical simulations.



Similar content being viewed by others
References
Allee, W.C., Emerson, A.E., Park, O.: Principals of Animal Ecology. Saunders, Philadelphia (1949)
Atkinson, A.: Life cycle strategies of epipelagic copepods in the Southern Ocean. J. Marine Syst. 15, 289–311 (1998)
Bainov, D., Simeonov, P.: Impulsive differential equations: periodic solution and applications. Longman, London (1993)
Beaugrand, G., Ibanez, F., Lindley, J.A.: Geographical distribution and seasonal and diel changes in the diversity of calanoid copepods in the North Atlantic and North Sea. Mar. Ecol. Prog. Ser. 219, 189–203 (2001)
Cui, J.A., Chen, L.S.: The effect of diffusion on the time varying logistic population growth. Comput. Math. Applic. 36(3), 1–9 (1998)
Davidson, F.A.: Growth and senescence in purebred jersey cows. University of lllinois Agricultural Experiment Station vol 302, pp. 192–199 (1928)
DeAngelis, D.L., Trexler, J.C., Donalson, D.D.: Competition dynamics in a seasonally varying wetland. In: Cantrell, S., Cosener, C., Ruan, S. (eds.) Spatial Ecology. chap 1, pp. 1–13. CRC Press/Chapman and Hall, London (2009)
DuBowy, P.J.: Waterfowl communities and seasonal environments: temporal variabolity in interspecific competition. Ecology 69, 1439–1453 (1988)
Funasaki, E., Kot, M.: Invasion and chaos in a periodically pulsed mass-action chemostat. Theor. Pop. Biol. 244(2), 203–224 (1993)
Gompertz, B.: On the nature of the function expressive of the law of human mortality and on a new method of determining the value of life contingencies. Philos. Trans. R. Soc. Lond. 115, 513–585 (1825)
Hsu, S.B.: A competition model for a seasonally fluctuating nutrient. J. Math. Biol. 9, 115–132 (1980)
Hsu, S.B., Zhao, X.Q.: A Lotka-Volterra competition model with seasonal succession. J. Math. Biol. 64(1), 109–130 (2012)
Hu, S.S., Tessier, A.J.: Seasonal succession and the strength of intra-and interspecific competition in a Daphnia assemblage. Ecology 76(7), 2278–2294 (1995)
Hui, J., Chen, L.-S.: A single species model with impulsive diffusion. Acta Mathematicae Applicate Sinica 21(1), 43–48 (2005)
Jiang, J.F., Niu, L., Zhu, D.J.: On the complete classification of nullcline stable competitive three-dimensional Gompertz models. Nonlinear Anal. RWA 20, 21–35 (2014)
Klausmeier, C.A.: Floquet theory: a useful tool for understanding nonequilibrium dynamics. Theor. Ecol 1, 153–163 (2008)
Klausmeier, C.A.: Successional state dynamics: a novel approach to modeling nonequilibrium foodweb dynamics. J. Theor. Biol. 262(4), 584–595 (2010)
Kocic, V.L., Ladas, G.: Global Behavior of Nonlinear Difference Equations of Higher Order with Application. Spinger, London (1993)
Lakmeche, A., Arino, O.: Bifurcation of nontrival periodic solution of impulsive differential equations arising chemotherapeutic treatment. Dyn. Cont. Dis. Impulsive Syst. 7, 265–287 (2000)
Li, J.X., Zhao, A.M.: Stability analysis of a non-autonomous Lotka-Volterra competition model with seasonal succession. Appl. Math. Model. 40(2), 763–781 (2016)
Litchman, E., Klausmeier, C.A.: Competition of phytoplankton under fluctuating light. AM Nat. 157, 170–187 (2001)
Liu, X.Z.: Impulsive stabilization and applications to population growth models. Rocky Mt. J. Math. 25(1), 381–395 (1995)
Liu, X., Zhang, S.H.: A cell population model described by impulsive pdes-existence and numerical approximation. Comput. Math. Appl. 36(8), 1–11 (1998)
Mayzaud, P., Tirelli, V., Errhif, A., Labat, J.P., Razouls, S., Perissinotto, R.: Carbon and role of zooplankton grazing in the Indian sector of the Southern Ocean. Deep-Sea. Res. II(49), 3169–3187 (2002)
Pearce, J., Ferrier, S.: An evaluation of alternative algorithms for fitting species distribution models using logistic regression. Ecol. Model 128, 127C147 (2000)
Smetacek, V., Scharek, R., Nothig, E.M.: Seasonal and regional variation in the pelagial and its relationship to the life history cycle of krill. In: Kerry, K.R., Hempel, G. (eds.) Antarctic Ecosystems: Ecological Change and Conservation, pp. 103–114. Springer, Berlin (1990)
Steiner, C.E., Schwaderer, A.S., Huber, V., Klausmeier, C.A., Litchman, E.: Periodically forced food chain dynamics: model predictions and experimental validation. Ecology 90(11), 3099–3107 (2009)
Taylor, R.A., Sherratt, J.A., White, A.: Seasonal forcing and multi-year cycles in interacting populations: lessons from a predator-prey model. J. Math. Biol. 67(6), 1741–1764 (2013)
Tello, J.I., Winkler, M.: Stabilization in a two-species chemotaxis system with a logistic source. Nonlinearity 25(5), 1413–1425 (2012)
Verity, P.G., Smetacek, V.: Organism life cycles, predation, and the structure of marine pelagic ecosystems. Mar. Ecol. Prog. Ser. 130, 277–293 (1996)
Wang, W.J., Li, Y.X.: Stabilization in an n-species chemotaxis system with a logistic source. J. Math. Anal. Appl. 432, 274–288 (2015)
Wang, L.M., Liu, Z.J., Hui, J., Chen, L.S.: Impulsive diffusion in single species model. Chaos Soliton. Fract. 33(4), 1213–1219 (2007)
Weymouth, F.W., McMillin, H.C., Rich, W.H.: Latitude and relative growth in the razor clam, siliqua patual. J. Exp. Biol. 8, 228–249 (1931)
Windson, C.P.: The Gompertz curve as a growth curve. PNAS 18(1), 73–83 (1932)
Wright, S.: Book review. J. Am. Stat. Assoc. 21, 494 (1926)
Yu, Y., Wang, W., Lu, Z.: Global stability of Gompertz model of three competing population. J. Math. Anal. Appl. 334, 333–348 (2007)
Zhang, L., Teng, Z.D.: The dynamical behavior of a predator-prey system with Gompertz growth function and impulsive dispersal of prey between two patches. Math. Meth. Appl. Sci. 39, 3623–3639 (2016)
Zhang, L., Teng, Z.D., Liu, Z.J.: Survival analysis for a periodic predator-prey model prey impulsively unilateral diffusion in two patches. Appl. Math. Model. 35(9), 4243–4256 (2011)
Zhang, L., Teng, Z.D., Donald, L., Ruan, S.G.: Single species models with logistic growth and dissymmetric impulse dispersal. Math. Biosci. 241(2), 188–197 (2013)
Acknowledgements
We thank the anonymous referees very much for their valuable suggestions and careful reading and checking this paper. This work was supported by the National Natural Science Foundation of P.R. China (11361059, 11271312), the Natural Science Foundation of Xinjiang Province of China (2014721014) and the Scientific Research Programmes of Colleges in Xinjiang (XJEDU2013I03).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Li, Y., Zhang, L. & Teng, Z. Single-species model under seasonal succession alternating between Gompertz and Logistic growth and impulsive perturbations. Int J Geomath 8, 241–260 (2017). https://doi.org/10.1007/s13137-017-0092-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13137-017-0092-9